一種平行接近的地磁梯度仿生導航方法

王瓊, 周軍

(西北工業大學 精確制導與控制研究所, 陜西 西安 710072)

地磁場具有相當豐富的參數信息，其與地球近地空間的任一點都存在對應關系，是導航領域的一種天然坐標系。有關地磁導航的研究應用最為廣泛的方式是地磁匹配導航，就是將飛行器導航路徑上的實測地磁信息與機載地磁先驗地磁圖進行相關匹配，以獲得飛行器的實測位置并解算導航信息[1-2]。這種方法可以克服慣導系統中誤差隨時間距離進行累積的缺陷，而且其具有自主性，抗干擾性能較強，能夠全天時、全天候和全地域地執行自主導航任務[3]，所以地磁導航已經成為目前較重要的一種導航方式。但是先驗地磁圖的繪制由于種種原因，其精確性和完整性難以得到保證。這就對地磁匹配導航這種對磁圖精度依賴性較高的導航方法產生了極大的制約。近年來種種研究表明，地球上許多生物都可以根據地球磁場信息來進行定位和導航[4]。美國、德國、英國等多個國家對生物的地磁導航行為進行了實驗驗證和分析研究，研究表明：鳥類[5]、海龜[6]、鮭魚[7]等生物都能夠利用地磁場信息對自身的航向進行校正，從而實現自主導航[8-9]；但是當其受到磁場干擾時，這些生物中的大部分都不能順利地到達目的地[10]。這些生物的歸巢、回溯等過程往往是長距離導航，顯然它們的腦細胞中不大可能儲存一副完整的地磁圖，完成長距離導航所利用的僅僅為目的地的地磁信息。

西北工業大學的劉明雍等人[11]受生物利用地磁信息進行導航行為的啟發，提出了一種基于時序進化策略的搜索方法，使得多參量收斂伴隨并指導導航搜索的進行。導航過程中采用“優勝劣汰”的進化搜索模式，引導載體趨勢性逼近目標點，因而導航過程也即航向角的尋優過程。但是其隨機游走的導航搜索方式導致航向角波動較大，路徑往往比較曲折，不能很好地應用于飛行器導航。

本文受其啟發，為探求一種能適用于飛行器的仿生導航方法，在以終點地磁多參量為目標值的趨勢仿生導航過程中，結合當前位置的地磁場梯度信息，提出一種不依賴任何先驗地磁數據信息的仿生導航算法，利用實測數據平行接近目的地數據這一思想進行航向角預測，從而引導飛行器不斷向目標點運動，最終完成導航。

1 地磁仿生導航策略

地磁場的參數信息會因地球上任一點的經、緯度和高度的不同而變化[12]。因此，地磁參量B可以描述為

B={B1,B2,…,Bn}

(1)

式中,Bi(i=1,2,…,n)為地磁參量元素,即地磁要素,是指表示地球磁場的方向和大小的物理量,由地磁場總強度F、水平強度H、磁偏角D、磁傾角I、磁場3分量X,Y,Z7個物理量組成。

仿生導航的目的是模仿生物快速安全地到達目的地,這種多目標收斂問題的目標函數Q可以描述為[13]

minQ(Bk,BT)=(q1,q2,…,qn),n=1,2,…,7

(2)

式中,Bk為飛行器當前位置k的地磁參量,BT為目標位置T的地磁參量;qi為第i個地磁參量Bi所對應的子目標函數,用來表示當前點與目標點之間的差異。仿生導航的任務就是使Bk中的n個參量在路徑約束下最終收斂到目標值BT。當目標值Q達到最小,即當多個地磁參量的q收斂為0或者達到最小的時候,即認為飛行器到達目標點T。

2 平行接近地磁梯度仿生導航算法

2.1 平行接近導航策略

平行接近的概念是2個飛行器在交會過程中,實現轉動速度在某一確定的坐標系為零,也就是2個飛行器之間的視線在接近過程中保持平行,如圖1所示。在此情況下,追蹤器就可以利用自身與目標器軌道速度差沿著視線方向接近目標[14]。平行接近法實現起來比較方便,而且彈道比較平直、導彈的過載比較小。

圖1 平行接近法的示意圖

圖2 地磁仿生導航平行接近法示意圖

以往的地磁仿生導航方法是在隨機游走的模型基礎上進行的,航向角變化豐富,不能很好地應用于飛行器導航。本文針對這一問題,設計了一種適用于飛行器的地磁仿生平行接近導航算法。如圖2所示,在飛行器向目的地接近的過程中,計算求得當前位置k的航向角θk,使按照此航向角行進的單位步長下,不同地磁參量Bi,k(i=1,2,…,n)能保持相同比值接近各自目標點的地磁值Bi,T,即

(Bi,k+1-Bi,k)∝(Bi,T-Bi,k)i=1,2,…,n

(3)

2.2 地磁梯度仿生導航算法

1) 飛行器運動方程

在一個二維平面內,飛行器的運動方程可表述為

(4)

式中,(x,y)表示飛行器所在的位置,u為系統輸入,也即與速度v和航向角θ相關的函數。

2) 航向角解算

假設飛行器的速度v是恒定的,那么導航輸入u直接由航向角θ決定,即u=θ。所以地磁仿生導航的過程也就是航向角θ的求取過程,如圖3所示。

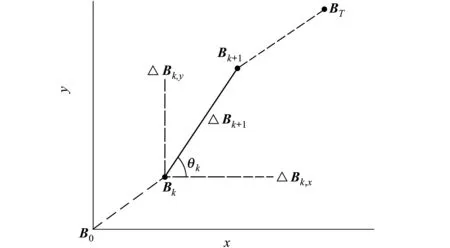
圖3 行進方向預測示意圖

圖中,ΔBk為當前位置k與前一位置k-1的地磁差值,ΔBk,x,ΔBk,y分別為其x軸、y軸方向的分量。為使不同地磁參量Bi,k能以相同比值Mk接近各自目標點的地磁值Bi,T,(3)式可進一步寫為

ΔBi,k+1=Mk·ΔBi,T,i=1,…,n

(5)

式中

根據平行接近導航策略,就是使下一時刻k+1相鄰兩步之間的地磁差值ΔBi,k+1平行接近當前點k與目標點T之間的差值ΔBi,T,也就是求得航向角θk,使當前位置k的不同參量比例系數相等,即Mi,k=Mj,k,(i≠j)。

(8)

(9)

由于上式中x軸、y軸方向的分量ΔBi,k,x和ΔBi,k,y并不好直接獲得,本文引入地磁場梯度進行計算。因為地磁梯度表示的是地磁場在某點范圍的變化量,假設k點與k+1點之間的距離足夠小,可以認為相鄰兩點之間地磁差值ΔBi,k,x與該分量的梯度值gi,k大致相等。證明如下[15]:

定義函數Bi(x,y)有關變量x的偏導數dBi可寫作

dBi(x,Δx,y)

(10)

如果Bi在x處可微,那么B的差值

ΔBi,xBi(x0,Δx,y)-Bi(x0,y)

(11)

滿足

(12)

式中,增量Δx近似滿足Δx→0。可以得到

ΔBi,x≈dBi(x,y)

(13)

地磁場梯度gi,k是安振昌學者[16]根據地磁場的高斯理論提出的

(14)

式中,gi,k,x和gi,k,y分別為地磁場梯度的x軸、y軸方向的分量。有關地磁場梯度具體的求導過程可以參考文獻[17]。

于是(9)式可以改寫為

(15)

從(15)式可以推導出

(16)

則航向角θk為

θk=arctan

(17)

由于反正切函數arctan(·)的取值范圍在[0,π]之間,因此在求取航向角θk時,應注意角度方向。

3) 評價指標

本文根據目標函數的收斂性構建了評價指標體系。這個指標可以通過當前位置的地磁值Bi,k和目的地的地磁值Bi,T之間的差異來描述。即

qi(k)=|Bi,k-Bi,T|i=1,…,n

(18)

則評價指標Q(k)可設置為

(19)

當評估指標Q(k)達到極小值ε時,可以認為飛行器到達目標點,導航過程完成。

4) 誤匹配點校正

假定地球磁場是一個理想的磁偶極子體,地球表面同一高度情況下的每個地磁場參量Bi的等值線都應該是一個圓。也就是說2個不同的地磁分量的等值線有可能存在2個交點P1和P2,而如果只用這2個地磁分量進行導航,在這2個交點處該分量地磁值是完全相同的,如圖4所示,這就會導致誤匹配問題。

圖4 導航誤匹配情況示意圖

但是當導航過程中P1和P2不在一個平面內的時候,2個地磁分量就可以完成導航任務。

眾所周知地磁場具有豐富的地磁信息,但已知其中任意獨立的3個地磁分量就可以推算出全部7個地磁分量。7個地磁分量間的相互推導關系見文獻[18]。為避免導航過程陷入誤匹配情況,本文引入第3個地磁分量對航向角進行輔助判斷。當一段連續時間內,2個不同地磁分量的評價指標qi(k)和qj(k)一直存在收斂趨勢,而第3個地磁分量的值ql(k)(l≠i,j)卻明顯開始增大,說明航向角求取過程陷入誤匹配點導航。此時需重新選取2個地磁分量在當前點重新開始導航過程。

本文創新性地利用平行接近方法進行地磁仿生導航,并借助地磁場梯度信息,用地磁場趨勢變化輔助航向角的求取。算法流程如圖5所示。

圖5 比例梯度導引算法流程

3 仿 真

為了驗證上述導航算法,本文采用國際地磁模型IGRF12模擬實際地磁場環境,并在Matlab中進行仿真驗證。

下面首先不考慮誤匹配情況,僅對本文所述平行接近地磁梯度仿生方法進行仿真實驗。仿真過程用經緯度表示飛行器的位置信息(x,y),設定導航速度v的值約為0.1°經緯度值的大小。當飛行器所在位置與目標點的磁測數據的差值達到某一較小范圍時,認為到達目的地,仿真結束。本次仿真任務中的評價指標設置為Q(k)<0.01。

1) 不同地磁參量作為導航線索

由于地磁場信息豐富,導航過程僅選取2種地磁參量用于解算導航信息,為說明本文方法的有效性,仿真過程中選取了如下3組不同的地磁分量進行實驗:A組的導航線索為地磁場東向分量Bx、北向分量By;B組的導航線索為地磁場垂直分量Bz、水平分量H;C組的導航線索為磁偏角D、磁傾角I。最終實驗結果如圖6所示。

圖6 從(-60,20)到(-50,5)的3組導航運動軌跡圖

上圖中導航起始點設置為(-60,20),目標點設置為(-50,5)。針對同一初始點到目標點的指令信息,仿真結果顯示,在沒有地磁圖先驗參考條件的情況下,采用本文地磁梯度仿生導航算法進行了3組實驗,其導航過程雖然呈現不一致的導航路徑,但最終均能完成導航到達目標點。

2) 相同地磁參量作為導航線索

關于相同的導航參量,選取不同的飛行路徑進行導航實驗。本次實驗中地磁參量選取磁偏角D、磁傾角I,從相同的初始位置(圖7中O點)開始,選取4個不同方向朝既定的目標位置(圖7中A,B,C,D點)運動。實驗結果如圖7所示。

圖7 相同導航參量的導航運動軌跡圖

圖7中,起始點O設置為(0,0)點,4個目標點的設置分別為A(20,-10),B(-10,-10),C(-10,20),D(10,15)。飛行器從起始點出發朝著4個不同的目標點飛行,隨著時間的累積,4組導航運動根據地磁場的變化都存在明顯逼近目標的趨勢,結果表明4組實驗都較好地完成了導航任務。

3) 與進化仿生導航的對比

為了與文獻[11]中所述進化地磁仿生導航方法進行對比,選取實驗2中導航運動軌跡OA作為參考,并同樣設置進化仿生導航方法的導航參量為磁偏角D、磁傾角I,仿真對比結果如圖8所示。

圖8 與進化仿生導航軌跡對比圖

從圖8可以看出,2種導航方法從同一起點(0,0) 點出發向目標點(10,15)前進,最終都能完成導航到達目標點。由于進化地磁仿生導航方法借鑒了隨機游走模型的思想,導航路徑雖能逐漸趨于收斂,但是其隨機搜索的過程導致航向角的變化較為豐富。本文方法的航向角θ隨著導航過程緩慢變化,整體來說變化過程較為平緩,相對更適合應用于飛行器進行導航任務。

綜合實驗1、2、3,當導航過程中不存在誤匹配點,即當P1和P2不在同一導航平面時,可以證明本文所述算法可以模擬無先驗地磁圖情況下的仿生導航過程。而且導航航跡路線比較平滑,基本滿足飛行器導航任務的需求。

4) 誤匹配點校正

前文對本文所述平行接近地磁梯度仿生方法進行了有效的驗證,在絕大多數情況下,采用本文方法都能很好地完成導航。但是地磁場信息豐富,僅采用2個地磁分量進行導航,難免會由于信息量缺失導致誤匹配,如圖9所示。為解決這種狀況,引入第3個地磁分量輔助進行導航,從而對匹配情況進行校正,如圖10所示。

圖9 導航信息誤匹配軌跡圖

圖10 誤匹配校正導航軌跡圖

圖9中,導航起點為(50,50),目標點設置為(70,40),直線表示的是飛行過程中沒有航向角約束的情況,虛線為存在航向角約束的飛行軌跡。從圖中可以看出,導航過程本應從起點出發往目標點行進,但是由于2個導航參量在誤匹配點(23.3,42.7)的地磁值與目標點(70,40)的地磁值相同,均為D=0.072 nT,I=1.036 nT,從而導致導航過程發生誤匹配情況。

為了解決這種誤匹配狀況,從導航過程起始就引入第3個地磁分量F進行輔助導航,如圖10所示。一段時間后對導航過程進行判斷,如果發現出現誤匹配導航狀況就采用其他地磁分量在當前點開始重新導航。同樣,直線為沒有加入飛行器航向角約束情況的飛行軌跡,虛線為存在航向角約束的誤匹配點校正導航飛行軌跡。圖9、圖10的航向角約束均設置為θlimit<15°。

綜上所述，本文方法可以較好地完成導航任務，并可以適用于飛行器的導航任務中。

4 結 論

本文針對地磁導航受地磁圖等先驗信息限制的問題，受平行接近法的啟發，結合地磁場梯度信息提出了一種平行接近地磁梯度仿生導航方法。利用地磁場梯度信息使當前位置的地磁參量平行接近目標信息，進行航向角求解，從而可不依賴任何地磁先驗信息進行地磁導航，并通過仿真驗證了該方法的有效性。

在實驗過程中發現，本文方法利用地磁梯度信息運用比例算法解算導航信息，在磁場信息較為平滑沒有地磁干擾情況下導航效果較好，若磁場曲線比較迂回或者存在地磁干擾將對整個導航過程造成較大的影響，有關這一問題將成為本文后續的研究重點。