基于缺口分析原理的裂紋擴展速率新模型

趙昆, 王生楠

(西北工業大學 航空學院, 陜西 西安 710072)

進行裂紋擴展分析的目的在于估算損傷細節的裂紋擴展壽命,即飛機結構的損傷在疲勞載荷作用下不斷擴展,裂紋從初始裂紋長度a0擴展到允許的終止裂紋長度ac所需的載荷循環次數/飛行時間。疲勞裂紋擴展速率da/dN-ΔK曲線是工程結構件損傷容限分析的重要依據,也是金屬材料的主要力學性能之一[1-4]。在20世紀中期,Yokobori以及Bathias、Bailon概括了一系列裂紋擴展的擬合模型[5],其基礎為Paris[6]、Forman[7]及Walker[8]公式,并通過這些公式得到了經典的裂紋擴展速率曲線。

在裂紋擴展分析過程中,通常將曲線分為3個區域。在區域Ⅰ中,存在應力強度因子門檻值ΔKth,當ΔK<ΔKth時認為裂紋是不發生擴展的,而一旦越過該門檻值之后,裂紋擴展速率會隨著ΔK的增加而快速的增長。在區域Ⅱ中,裂紋擴展速率與ΔK呈線性關系。而在區域Ⅲ中,裂紋擴展速率繼續上升而逐漸無限的接近于某條漸近線,即材料的斷裂韌度。對于傳統的裂紋擴展速率分析方法而言,使用Paris公式得到的da/dN-ΔK曲線僅僅能夠很好地描述區域Ⅱ內裂紋的擴展行為,通過Forman公式所獲得的裂紋擴展速率擬合曲線也僅僅增加了對區域Ⅲ的描述[9]。而對裂紋擴展分析而言,希望獲得的是能夠完整描述裂紋擴展行為的擬合曲線,而并非其中的某一部分,這就是本文提出新模型的初衷。

針對現有的da/dN-ΔK曲線不能有效地表示裂紋在整個擴展期內擴展行為的問題,本文依據Weiss缺口模型,在合理的范圍內對已有的裂紋擴展速率模型提出了新的假設,從而得到一個新的裂紋擴展速率模型,有效地描述了裂紋在低擴展速率及高擴展速率區域的擴展行為,并利用已有的試驗數據對該模型進行了驗證,結果表明:該模型能夠有效地表示裂紋在初始階段及臨近破壞階段的裂紋擴展行為,為裂紋的擴展提供了一個完整的分析擬合曲線,為之后的裂紋擴展分析打下了良好的基礎。

1 疲勞裂紋擴展速率模型

疲勞裂紋擴展從微觀的角度來看,可以認為是裂紋尖端的疲勞單元(fatigue elements)受到剪應力或拉應力作用而發生了一系列的斷裂行為而導致的,如圖1所示。Weiss認為,在循環載荷的每一次作用下,裂紋發生擴展的距離與最大法向應力σmax超過疲勞單元的臨界斷裂應力σff的有效范圍值是存在一定聯系的,并據此提出了缺口根部應力分布的彈性解模型[10],即

(1)

式中,σy為缺口根部應力,Kt為理論彈性應力集中系數,ρ為缺口根部的半徑,σN為名義應力。

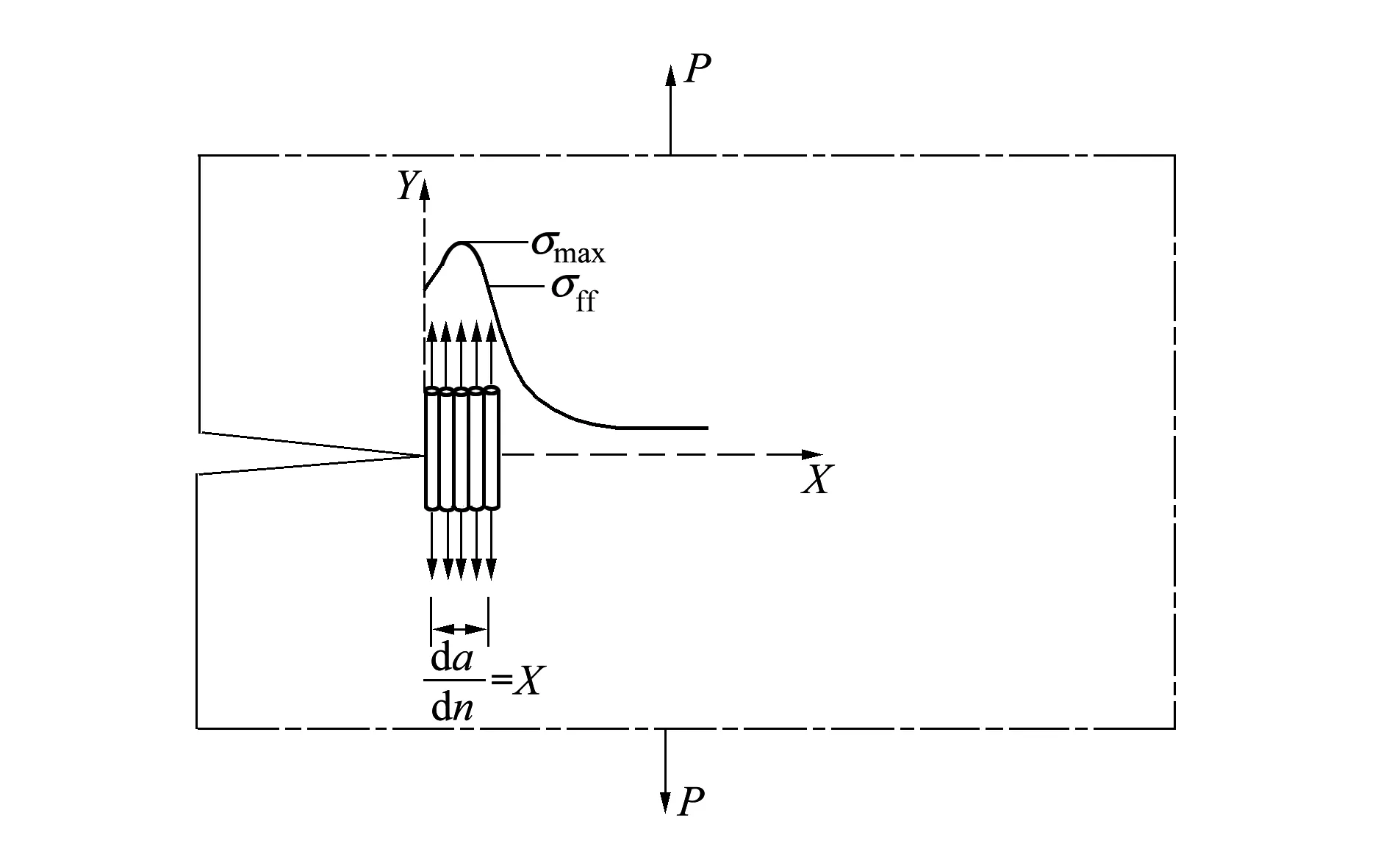
圖1 裂尖疲勞單元及裂尖應力場分布

考慮應力比R=0的情況,從微觀角度來看,裂紋的擴展行為經歷了以下幾個階段:

1) 當外載荷為零時,裂紋保持原有的閉合狀態,裂尖半徑可以忽略不計;

2) 當外載荷增加至某個值時,應力強度因子K達到門檻值Kth,此時裂紋張開且裂尖發生鈍化行為,但此時裂紋并沒有發生擴展;

3) 載荷繼續增加,裂尖前移并進一步發生鈍化;

4) 當外載荷增加到最大值時,裂尖前移至距離原裂紋尖端位置ΔL處,此時裂紋尖端的鈍化形態也最為明顯;

5) 卸載過程與加載過程相反,直至最后外載恢復至零,此時裂紋完全閉合。但從宏觀上來看,裂紋發生了擴展且擴展的距離為ΔL。

在上述1)～4)的裂紋擴展過程中,裂尖發生了鈍化行為,因此認為裂尖處的曲率半徑ρ′是真實存在的,且有ρ′≠0。此時做進一步的假設,將裂尖鈍化時的曲率半徑ρ′等效為缺口根部半徑ρ。基于此假設,可以將擴展中的某條裂紋近似等效為一個缺口來進行分析。

Inglis經過驗證得到橢圓形中心孔長軸端的彈性應力集中系數[14],即

例如求函數y=（sinx+2）/（cosx-2）的值域。很多學生拿到題目的第一反應是將函數變形化解為sin（x+θ）的形式，然后再根據三角函數的有界性進行計算。但教師在習題計算過程中可以引導學生運用數形結合的思想，繪制單位圓，在單位圓上找出定點（2，-2），將三角函數問題轉化成動點（cosx，sinx）在限定條件下的斜率問題。

(2)

(3)

將上述關系代入(2)式可以得到

(4)

考慮到裂紋尺寸與假設變量ρ*存在數量級上的差距,即2a?ρ*,則可以進一步得到如下關系

(5)

式中,2a為穿透裂紋的長度。根據Neuber法則[12]及應力應變關系,即

(6)

σ=kεη

(7)

式中,Kσ,Kε分別為真實應力、應變集中系數,η為應變硬化指數。

進一步對(6)～(7)式進行轉化,可以得到Kσ與Kt之間的關系,即

(8)

由于Weiss提出的缺口模型僅能代表彈性情況下的應力場分布,而無法代表裂尖前緣塑性區的應力分布,因此進一步假設,用真實應力集中系數代替(1)式中的理論應力集中系數,并對所得到的數學表達式進一步進行處理,得到缺口根部的真實應力場分布如下所示

(9)

(10)

依據Weiss提出的理論,裂紋尖端受到一次循環載荷作用時擴展的距離x為在當前應力場分布下σy取σff時所對應的x值,即裂紋擴展速率可以表示為

(11)

(11)式即為本文提出的裂紋擴展速率分析的新模型,該模型僅與名義應力和臨界斷裂應力相關,而與應力強度因子無關。

對(11)式進行簡化,兩邊取對數,則有

(12)

在圖1所示的區域Ⅱ中,由于裂紋擴展速率較快,有ρ*?Δa,因此ρ*/2a可以忽略不計。在本文的假設中,認為η和σff均為常數,且η的取值可以通過相關的手冊查得。將(12)式所表示的曲線置于雙對數坐標系中,則我們可以得到一條關于d(lna)/dN-σN的直線,斜率為(η+1)/η。根據所使用材料已知的應變硬化系數η,帶入(12)式中進行計算便可獲得σff的值。

在裂紋擴展速率曲線的區域Ⅰ內,我們認為裂紋擴展速率曲線與區域Ⅱ中直線段的延長線之間的偏離量正是由于ρ*/2a的存在所導致的。因此,沿X軸方向取3個點在實際偏移曲線上所得到的Y值與在區域Ⅱ中直線段的延伸線上獲得的Y值之間的差值,分別記為d1,d2,d3,則存在以下關系

(13)

進而利用(12)式即可得到ρ*的值。

2 算 例

本節對該裂紋擴展速率模型進行驗證。本節選取了Al2024-T351、Al7075-T6 2種鋁合金板材(厚度為3.5 mm,寬度為100 mm)的相關試驗數據作為原始分析數據,對模型的有效性進行驗證。對各個試樣的原始數據利用(12)式、(13)式計算獲得相應參數的取值見表1,表中的來源均指相應參考文獻編號。

表1 材料的相關參數

在應力比R=0.1的情況下,將上述數據分別帶入(12)式中。在MATLAB中采用遞增多項式函數[12]分別對2種不同材料參數所獲得的公式進行數值擬合,分別如圖2中a)、b)所示。圖3為2種材料使用經典裂紋擴展速率模型得到的裂紋擴展速率曲線。

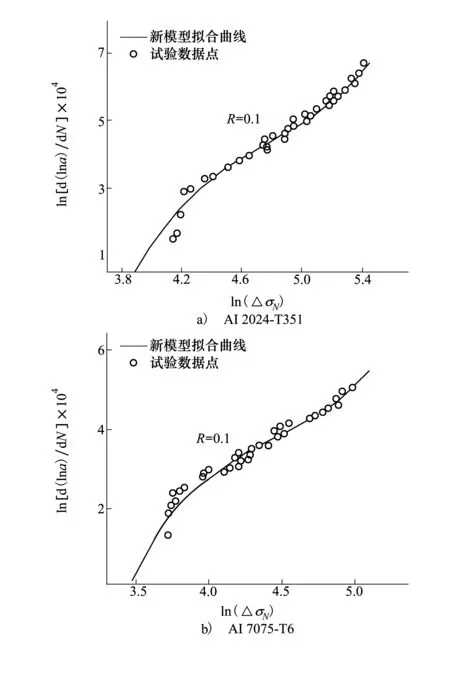
圖2 Al2024-T351和Al7075-T6裂紋擴展速率新模型曲線圖

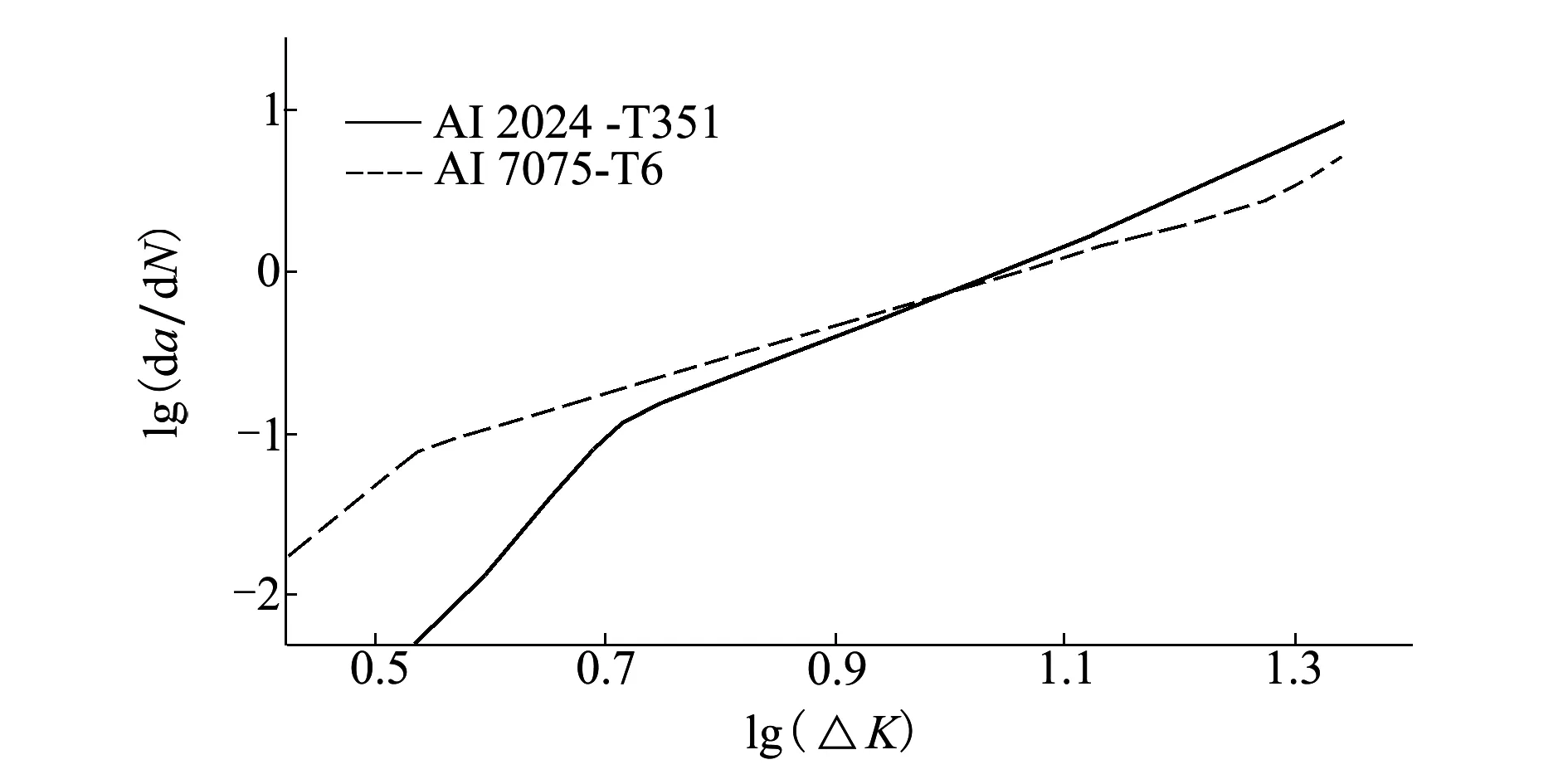
圖3 Al2024-T351和Al7075-T6傳統裂紋擴展速率曲線圖

對比圖2和圖3可以得到以下結論:本文提出的新模型擬合得到的裂紋擴展速率曲線與使用傳統模型得到的曲線走勢是大致相同的,說明本文的新模型符合裂紋擴展的基本規律。

與此同時,相對于傳統模型得到的裂紋擴展速率曲線而言,新模型表示的裂紋擴展行為從起始的擴展區域Ⅰ向區域Ⅱ過渡時顯得更為平滑,避免了曲線中的轉折點,對裂紋擴展行為的描述更為準確。因此本文提出的新裂紋擴展速率模型是可行的,準確性更高。

最后,新模型曲線對裂紋擴展的3個階段能夠更清晰地進行展示。在裂紋擴展高速率區域,新模型曲線逐漸接近于漸近線,而圖3中無法對高速率區域的裂紋擴展行為進行有效的描述。因此本文提出的新裂紋擴展速率模型是可行的,準確性更高。

3 結 論

本文基于Weiss提出的缺口應力分布模型,提出了新的假設并引入了新的裂尖半徑參數ρ*,得到新的裂紋擴展速率模型,并通過試件Al2024-T351及Al7075-T6已有的試驗數據,驗證了該模型的有效性。本文提出的新模型相較于傳統模型有:

1) 相較于使用Paris或Walker公式擬合得到的da/dN-ΔK曲線,新模型所得到的裂紋擴展曲線更貼切于真實的裂紋擴展情況,避免了曲線中的折點,能夠更好地對裂紋擴展行為進行描述。

2) 傳統模型無法很好地表示裂紋在擴展高速率區的擴展行為,而新模型在裂紋擴展高速率區的走勢接近于某條漸近線,即臨界破壞應力,這點與傳統裂紋擴展速率曲線趨勢一致。

3) 對于低應力比的情況,傳統的裂紋擴展模型均具有較好的準確度,但隨著應力的增大,傳統模型的研究結果會發生較大失真,這不僅僅是由于模型本身的因素,模型中的參數數量也給模擬和計算帶來了困擾。而新模型中涉及的3個參數均有自身的物理意義,可以通過模型本身的分析及數據手冊獲得,取值時波動性不大,并且在擬合過程中采用了高次數遞增多項式函數,其模擬結果偏保守,保證了模型的有效性。

在新模型的假設中,我們認為試件尺寸遠大于裂紋長度,此時試件被認為是一個無限大板。但在實際的工程應用中,必須考慮裂紋長度與試件尺寸的關系。為此在以后的研究中需要對本文提出的新模型考慮引入一個無量綱的修正系數f(a/w),以便有效反映裂紋長度與試件尺寸之間的關系,并且考慮到不同類型的裂紋,例如單邊裂紋、雙邊裂紋及中心裂紋等,該修正系數應當有不同的表達形式。其次,本文所考慮的裂紋為中央穿透裂紋,沒有對其他類型的裂紋進行更深入研究,具有一定的局限性。因此,仍需要對新模型進行修正和完善,使其應用范圍更為廣泛。