懸掛式單軌最小平面曲線半徑及緩和曲線長度研究

譚小波

(西南交通大學土木工程學院，四川成都 610031)

懸掛式單軌，又被稱為“空鐵”，最早在德國建成，近年來在我國興起。由于懸掛式單軌具有建設快、占地少、造價低、環境適應能力強、視覺效果好等優勢，因此在我國具有很大的發展潛力[1-3]。

在國外，只有德國和日本具有成熟的懸掛式單軌運營經驗，國內的懸掛式單軌建設腳步越來越快，但是尚無統一的技術標準和設計規范。因此，研究懸掛式單軌線路設計參數十分重要。本文借鑒傳統鐵路設計理論和經驗，從運行安全性、乘客舒適性的角度，對懸掛式單軌最小平面曲線半徑和緩和曲線長度進行研究。

1 懸掛式單軌結構特點

懸掛式單軌鐵路是單軌鐵路的一種，其軌道在上、車輛在下，車體懸掛在軌道梁下方。懸掛式單軌主要由軌道梁、車輛、車站、道岔、通信系統、供電系統等部分組成，懸掛式單軌車輛可分為轉向架、懸掛裝置和車體[4-5]。懸掛式單軌基本結構如圖1所示。

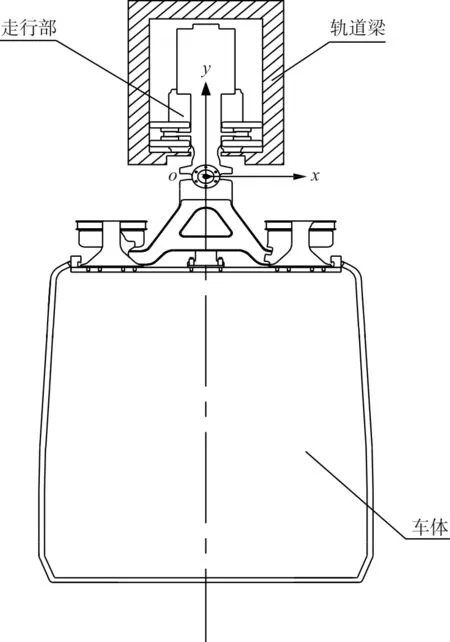
圖1 懸掛式單軌基本結構

懸掛式單軌的主要結構特點有：(1)懸掛式單軌的轉向架位于鋼制的、開口向下的軌道梁內，一般不存在脫軌可能。(2)車體與轉向架之間通過牽引懸掛裝置連接，牽引懸掛裝置包括中心銷、橫擺減振器等。列車通過平面曲線時，橫擺減振器會在一定程度上限制車體的橫向偏轉。(3)列車通過平面曲線時，車體會發生偏轉，能在一定程度上抵消行駛時產生的離心力，因此不設超高。懸掛式單軌車體的偏轉如圖2所示。

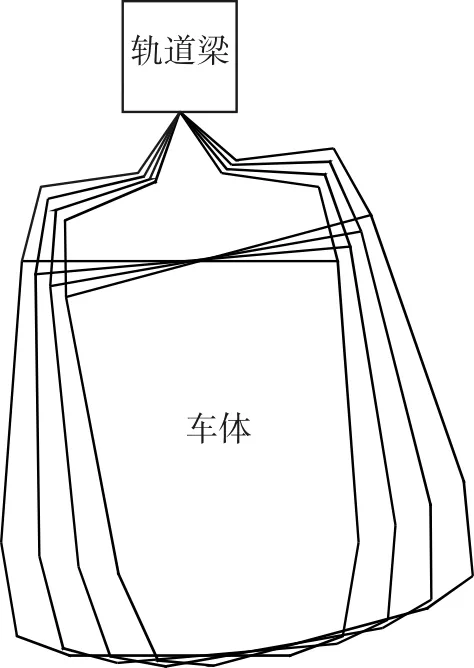
圖2 懸掛式單軌車體偏轉

2 懸掛式單軌最小平面曲線半徑

2.1 最小平面曲線半徑設計原則

在傳統鐵路中，列車通過曲線時，如果平面曲線半徑R過小，則速度V產生的離心加速度大于外軌超高產生的向心加速度，由此出現未被平衡的離心加速度。在傳統鐵路中，未被平衡的離心加速度用欠超高hq來表示。在傳統鐵路參數設計中，最小平面曲線半徑的設計原則是：保證列車以最高速度Vmax通過時，欠超高hq不超過允許值hqy，以保證旅客舒適度[6]。

對懸掛式單軌而言，當懸掛式單軌通過平面曲線時，車體在離心加速度的作用下會發生橫向擺動，車體向曲線外側偏轉一定角度。若車體與轉向架之間完全無約束，則車體的偏轉角度完全由離心力決定，此時車體重力在向心方向的分力正好等于離心力，不存在未被平衡的離心加速度。然而在實際情況中，由于車體與轉向架之間存在橫向減振器、摩擦阻力等，使得車體的偏轉角度達不到平衡離心力所需的角度，此時就產生了未被平衡的離心加速度。懸掛式單軌的參數設計方法參考傳統鐵路，但由于懸掛式單軌不設超高，在其最小平面曲線半徑的設計原則中，應把“欠超高不超過允許最大欠超高”改為“未被平衡的離心加速度不超過允許最大值”。同時，在懸掛式單軌中，若平面曲線半徑R過小，則速度V產生的過大離心力會使車體橫向偏轉角過大，從而影響乘客舒適度。所以在懸掛式單軌最小平曲線半徑的設計原則中，還應考慮車體的最大偏轉角。

綜上所述，懸掛式單軌最小平面曲線半徑的設計原則為：(1)保證列車以最高速度Vmax通過時，未被平衡的離心加速度不超過允許最大值。(2)保證列車以最高速度Vmax通過時，車體最大偏轉角不超過允許值。

2.2 最小平面曲線半徑公式推導

在懸掛式單軌中，未被平衡的離心加速度可以表示為：

式中：aq為未被平衡的離心加速度(m/s2)；V為懸掛式單軌運行速度(km/h)；R為經過的平面曲線半徑(m)；g為重力加速度值，取9.8m/s2；θ為車體橫向偏轉角(rad)。

設未被平衡的離心加速度允許值為aqy，車體橫向最大偏角允許值為θy。由于aq≤aqy，θ≤θy，所以若已知aqy和θy的大小，則最小平面曲線半徑可以表示為：

式中：Rmin為懸掛式單軌最小平面曲線半徑(m)。

由該公式可知，只需得到aqy和θy的取值大小，帶入該公式，即可得到懸掛式單軌最小平面曲線半徑Rmin與其運行速度V之間的關系。

2.3 最大偏轉角允許值

在傳統鐵路中，為了保證列車不內向傾覆，同時保障乘客舒適，需要限制外軌超高的最大值。外軌超高越大，列車的偏轉角越大，乘客越不舒適。對比可知，懸掛式單軌的最大偏轉角與傳統鐵路中的外軌最大超高類似。同時，懸掛式單軌由于對車輛結構和車內設施進行了優化，且運行的速度比較一致，從而提高了舒適性，這兩點與傳統鐵路中的客運專線類似。所以可參考客運專線的外軌超高允許值來計算懸掛式單軌的最大偏角允許值。

查閱相關資料[7]，客運專線實設超高最大允許值取180 mm，可將該值換算為客運專線的最大偏轉角，然后用于懸掛式單軌中。在客運專線中，由幾何關系：

式中：θy為最大偏轉角允許值(rad)；hy為客運專線實設超高最大允許值(mm)；S為兩根鋼軌軌頭中心線之間的距離(mm)。

帶入hy=180 mm，S=1 500 mm(標準軌)，算得最大偏轉角θy=6.892°=0.12 rad。

2.4 未被平衡的離心加速度允許值

根據我國城市軌道交通設計運營經驗，未被平衡的離心加速度允許值取0.4 m/s2比較合適[8]。本文建議在懸掛式單軌中aqy取0.4 m/s2。

2.5 最小平面曲線半徑取值

將θy=6.892°=0.12 rad和aqy=0.4 m/s2帶入Rmin的計算公式，并取g=9.8 m/s2，得懸掛式單軌最小平面曲線半徑：

式中，Rmin為懸掛式單軌最小平面曲線半徑(m)；V為懸掛式單軌運行速度(km/h)。

建議懸掛式單軌最小平面曲線半徑以該式計算，同時，為了測設、施工和養護的方便，建議把結果進整為10 m的整倍數，得懸掛式單軌不同設計速度下的最小平面曲線半徑值，如表1所示。

表1 懸掛式單軌最小平面曲線半徑值

實際施工中，如果遇到特殊條件，導致懸掛式單軌平面曲線半徑取值困難，可經過技術經濟比選后在上表的基礎上選擇適當較小的值。

3 懸掛式單軌緩和曲線長度

3.1 緩和曲線長度設計原則

在傳統鐵路中，緩和曲線長度影響行車安全和旅客舒適，在擬定緩和曲線長度標準時，根據下列三個條件各自計算并取其中的較長者[6]。條件一：超高順坡不致使車輪脫軌；條件二：超高時變率不致使旅客不適；條件三：欠超高時變率不致使旅客不適。

根據傳統鐵路設計經驗，當列車低速運行時，上述條件一算出的緩和曲線最長，起控制作用；當列車中速運行時，上述條件二起控制作用；當列車高速運行時，上述條件三起控制作用。

對懸掛式單軌而言，由于其不設超高，且其走行部分包裹在軌道梁內，不存在脫軌問題，所以擬定其緩和曲線長度時無需考慮上述條件一。懸掛式單軌經過緩和曲線時車體會逐漸發生橫向偏轉，稱其橫向偏轉的角速度為“傾斜時變率”[9]。懸掛式單軌在直線上橫向偏轉角為零，在圓曲線上橫向偏轉角不為零，若緩和曲線長度過短，則經過緩和曲線所用時間(過渡時間)較少，勢必導致傾斜時變率過大，影響旅客舒適度。可以發現，這里的傾斜時變率類似于傳統鐵路中的超高時變率，兩者都刻畫了車體偏轉的速度，兩者過大都會造成旅客不舒適。所以在擬定懸掛式單軌緩和曲線長度時，參考上述條件二，并把“超高時變率不致使旅客不適”改為“傾斜時變率不致使旅客不適”。

同時，懸掛式單軌在直線上未被平衡的離心加速度為零，在圓曲上未被平衡的離心加速度不為零。則未被平衡的離心加速度在過渡的緩和曲線上越來越大，稱其變化的速度為“未被平衡的離心加速度時變率”。若緩和曲線長度過短，則經過緩和曲線所用時間(過渡時間)較少，勢必導致未被平衡的離心加速度時變率過大，影響旅客舒適度。如前文所述，在傳統鐵路中，未被平衡的離心加速度用欠超高來表示，那么上述條件三中的“欠超高時變率”實際上表示的應該是“未被平衡的離心加速度時變率”。所以在擬定懸掛式單軌緩和曲線長度時，參考上述條件三，并把“欠超高時變率不致使旅客不適”改為“未被平衡的離心加速度時變率不致使旅客不適”。

綜上所示，懸掛式單軌最小緩和曲線長度的設計原則為：(1)傾斜時變率不致使旅客不適。(2)未被平衡的離心加速度時變率不致使旅客不適。

由于此處的原則1、2分別繼承于傳統鐵路緩和曲線設計中的條件二、三。所以參考傳統鐵路設計經驗，當速度較低時，應該是原則(1)算出的緩和曲線較長，起控制作用；當速度較高時，應該是原則(2)起控制作用。而懸掛式單軌的設計速度基本在50～70 km/h，相對較低，此時原則(1)起控制作用。于是在計算懸掛式單軌最小緩和曲線長度時，先以原則(1)計算，然后把原則(1)的計算結果帶入原則(2)檢驗，若檢驗通過，則說明該結果同時滿足原則(1)、(2)，以該結果進行懸掛式單軌最小緩和曲線取值是合理的。

3.2 基于傾斜時變率的緩和曲線長度計算

3.2.1 基于傾斜時變率的緩和曲線長度公式推導傾斜時變率可以表示為：

式中：w為懸掛式單軌傾斜時變率(rad/s)；θ為車體橫向偏轉角(rad)；t為通過緩和曲線所用時間(s)。

其中：

式中：L為懸掛式單軌緩和曲線長度(m)；V為懸掛式單軌運行速度(km/h)。

所以傾斜時變率w可表示為：

設最大傾斜時變率允許值為wy，由于w≤wy，若已知wy的大小，則懸掛式單軌緩和曲線最小長度可以表示為：

式中：Lmin為懸掛式單軌緩和曲線最小長度(m)。

其中，需要對車體橫向偏轉角θ進行計算。如前文所述，在實際情況中，由于車體與轉向架之間存在橫向減振器、摩擦阻力等，使得車體的偏轉角度達不到平衡離心力所需的角度，即：

由于各廠家生產的懸掛式單軌車輛系統參數不同，且各參數對θ的影響機制復雜，導致難以得到一個普遍適用的、準確的θ的解析表達式。但是從實用性和安全性的角度來看，求Lmin不必先得到θ的準確表達式，可以對θ進行放縮，得到θ的一個適當偏大的值，由此計算出的Lmin也是適當偏大、偏安全的，可滿足實際需要。即令：

且車體橫向偏轉角θ一般很小，所以有：

θ≈tanθ

于是得到θ的近似表達式：

如前文所述，該表達式求出的θ來計算Lmin是偏安全的，所以在本文中用此方法近似求θ是科學的。

將θ的表達式帶入Lmin，得：

3.2.2 最大傾斜時變率允許值

如前文所述，懸掛式單軌中的傾斜時變率類似于傳統鐵路中的超高時變率，那么就可以參考傳統鐵路中的超高時變率允許值來擬定懸掛式單軌中的最大傾斜時變率允許值。

在傳統鐵路中，超高時變率表示為:

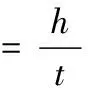
式中：h為傳統鐵路中圓曲線上的外軌超高(mm)；t為通過緩和曲線所用時間(s)。

由幾何關系：

h=S·sinθ

式中：S為兩根鋼軌軌頭中心線之間的距離(mm)，在標準軌中S=1 500 mm；θ為車體橫向偏轉角(rad)。

設超高時變率允許值為f，當：

反解出：

將t帶入w，得：

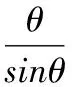
式中，wy為最大傾斜時變率允許值(rad/s)。

我國在制定相關標準時，超高時變率允許值f的取值為：城際鐵路，一般條件下取28 mm/s，困難條件下取35 mm/s[10]；客運專線鐵路，良好條件下取25 mm/s，一般條件下取28 mm/s，困難條件下取31 mm/s[11]；地鐵(其最高設計速度為100 km/h)，f取40 mm/s[12]。

可以發現f的變化規律：隨著設計速度降低，f逐漸變大，換算出的wy自然也相應變大。對于懸掛式單軌，國內不同廠家生產的懸掛式單軌車輛的設計速度基本在50～70 km/h，比地鐵的設計速度還低，所以本文建議以f=45 mm/s進行wy的換算。帶入wy的計算公式，得：

3.2.3 基于傾斜時變率的緩和曲線長度取值

將wy=0.03 rad/s帶入Lmin的計算公式，并取g=9.8 m/s2，得懸掛式單軌最小緩和曲線長度：

式中：Lmin為懸掛式單軌最小緩和曲線長度(m)；V為懸掛式單軌運行速度(km/h)；R為平面圓曲線半徑(m)。

建議懸掛式單軌最小緩和曲線長度以該式計算，同時，為了測設、施工和養護的方便，建議把結果進整為5 m的整倍數，最小取10 m。得懸掛式單軌不同設計速度下常用曲線半徑的緩和曲線長度值，如表2所示。

表2 懸掛式單軌緩和曲線長度

實際施工中，如果遇到特殊條件，導致懸掛式單軌緩和曲線取值困難，可經過技術經濟比選后在上表的基礎上選擇適當較小的值。

3.3 基于未被平衡離心加速度時變率的緩和曲線長度檢算

設未被平衡離心加速度時變率為β，設未被平衡離心加速度時變率的允許值為βy。懸掛式單軌的乘客乘車環境與地鐵的乘車環境類似，所以參考我國地鐵設計規范[12]，取βy=0.3 m/s3。由：

式中：β為未被平衡離心加速度時變率(m/s3)；aq為未被平衡的離心加速度(m/s2)；t為經過緩和曲線所用時間(s)；L為緩和曲線長度(m)；V為行車速度(km/h)。

可得：

在滿足平面曲線半徑取值要求的情況下，將上文基于傾斜時變率的緩和曲線長度值帶入β計算公式，若由此算出的β最大值βmax滿足：

βmax<βy(βy=0.3m/s3)

則檢算通過。

其中，當aq=0.4 m/s2(在滿足平面曲線半徑取值要求的情況下，取aq的最大值)時，β取得最大值βmax。由前文：

所以，當aq=0.4 m/s2時，必有：

即：V2>5.184R(β取得最大值βmax的必要條件)。

此時，將上文基于傾斜時變率的緩和曲線長度值帶入β計算公式，有：

(其中V2>5.184R)<0.3

說明基于傾斜時變率的緩和曲線長度值同時也滿足未被平衡的離心加速度時變率不超限，檢算通過。實際應用中，可以用基于傾斜時變率的緩和曲線長度計算公式來計算懸掛式單軌緩和曲線長，表2的取值是科學的。

4 結論

(1)根據傳統鐵路經驗，懸掛式單軌車輛最大偏轉角不宜大于6.892°，最大未被平衡離心加速度取0.4 m/s2。(2)得到了懸掛式單軌最小平面曲線半徑計算公式，不同設計速度下懸掛式單軌的最小平面曲線半徑值如表1所示。(3)根據傳統鐵路經驗，懸掛式單軌最大傾斜時變率不宜大于0.03 rad/s，最大未被平衡離心加速度時變率取0.3 m/s3。(4)得到了懸掛式單軌最小緩和曲線長度計算公式，不同設計速度下常用曲線半徑的緩和曲線長度值如表2所示。