典型風向下平屋蓋低矮結構的流場研究

蒲云迪，程 旭,孫 毅，李天成，李 藝

(西南交通大學土木工程學院，四川成都 610031)

近年來大跨屋蓋結構應用廣泛，其結構形式趨于長大化、輕質化，具有阻尼小、自有頻率低的特點，風荷載因此成為設計時的決定性因素之一。CFD相較風洞試驗具有周期短、可控參數多、后處理限制少等優點，若能合理安排計算成本與結果精度的矛盾，即可為風場研究提供有力依據。

目前對孤立建筑風場乃至干擾效應風場的研究以風洞試驗為主。Ho等[1]基于孤立低矮建筑街區的風洞試驗數據,從概率統計的角度推薦了一種分析周邊障礙物對被包圍低矮建筑風荷載影響的方法。其周邊障礙物可以是隨機出現的低矮建筑、樹木、圍墻或停車場等。在他的風洞試驗中,周邊建筑環境工況只有一個,沒有研究周邊建筑環境參數的變化。田村幸雄等[2-5]使用風洞試驗全面研究了若干個建筑的干擾效應，考慮了建筑密度CA、上游距離Lfetch、建筑群排布、建筑相對高度Hr、風角θ對流場和荷載的影響，發現在典型風向90°下周邊建筑由放大干擾轉為遮蔽效應(Channeling Effect)。

目前對孤立建筑風場乃至干擾效應風場的研究均以風洞試驗為主，而較少有系統的CFD研究。本文使用大渦模擬(LES)的Smagorinsky亞格子應力模型進行數值模擬，分析3個典型風向下孤立的平屋蓋低矮建筑的流場，并與北京交通大學回流式風洞的試驗數據進行對比。

1 試驗工況和計算參數

1.1 模型設計和邊界層模擬

試驗模型中施繞建筑和受擾建筑尺寸相同，均設置為(B,H,L)=(3 m,0.8 m,2 m)。模型幾何比尺為1∶200，速度比尺為1∶1。每個模型設置125個測點(其中屋面59個)，經過測量并修正得到30 000步風壓序列。取屋面為參考高度，參考風速為9.59 m/s。采用粗糙元(70 cm×70 cm)和尖劈的布置模擬開闊地帶的邊界層來流。在試驗中通過皮托管測得各高度出的平均風速，然后擬合得到實際粗糙度指數α=0.1299。風洞布置和測點布置如圖1所示。平屋蓋結構的風壓系數有明顯的區域性，角部風壓分離明顯，為了與測點方案配合，將屋按圖2分為9個區域[8]，如圖2所示。

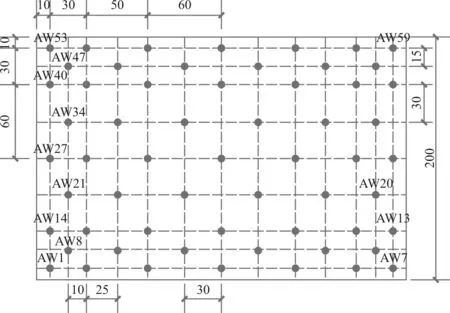
圖1 風洞試驗屋面測點布置

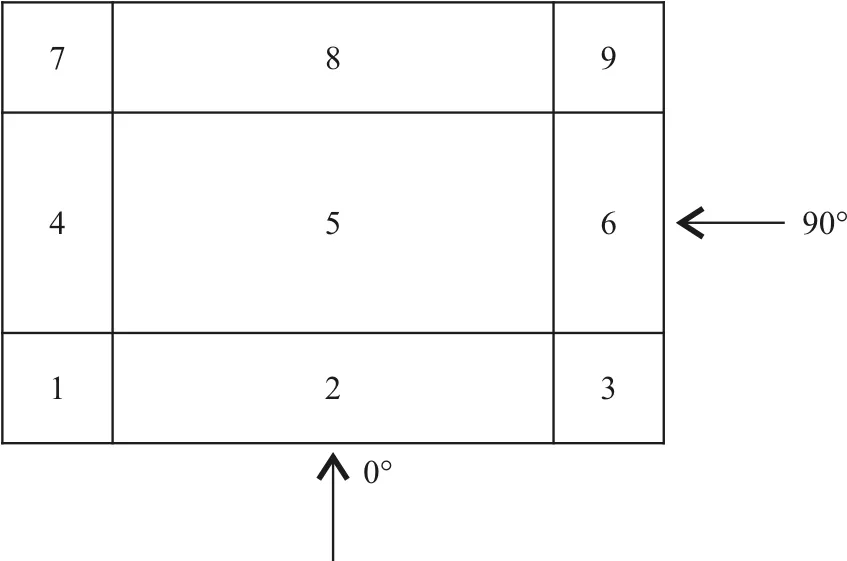
圖2 屋面分區方案

數值模擬方面，按照上述參考高度、平均風速、粗糙度指數在Fluent17.0中結合F_PROFILE()宏寫入UDF，以獲得符合上述指數率的入口平均風速剖面。

1.2 網格和算法細節

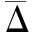
(1)

(2)

基于ICEM軟件為平屋蓋建筑劃分結構化網格。計算域在流向、橫向、展向的尺寸分別為(5+15)L、(5+15)B、10H，阻塞比小于3 %。為滿足無量綱數y+<50的要求，近壁面第一層網格尺度為1 mm。對建筑周圍進行加密，網格總數分別為200萬、260萬。另外建立同參數的空網格，計算臨建筑前的速度場，以驗證風剖面的正確實現。

建筑表面和地面采用無滑移邊界，頂面采用自由滑移邊界，兩側面為對稱邊界(Symmetry)，出口為壓力出口邊界(Pressure-outlet)。采用SIMLEC離散格式，基于CFL條件設置時間步長為0.001 s，每步最大迭代次數為20。設置收斂條件為殘差無窮小，并在屋面中心附近(11,16.5,0.9)設一監測點，檢測其流向速度，作為流場平穩的依據,如圖3所示。

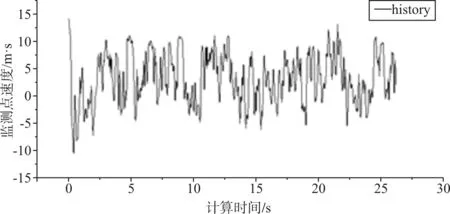
圖3 監測點流向速度時程

2 結果分析

求解了三個風向下孤立建筑的速度風剖面、單體的平均風壓力以及基底力矩系數，并與北京交通大學回流式風洞的試驗數據進行對比。

2.1 速度風剖面

圖4是加載UDF并計算穩定后后，CFD模擬空計算域中臨建筑處的速度剖面和風洞實測速度剖面的對比。至于湍流強度，由于本文關注風壓和荷載的時均值而不涉及極值，所以使用譜合成速度方式，即在入口處人工指定湍流度沿高度方向為常數0.25，即可得到準確的時均值。但此種方法由于未考慮湍流強度的變化，無法捕捉到準確的風壓和荷載極值。

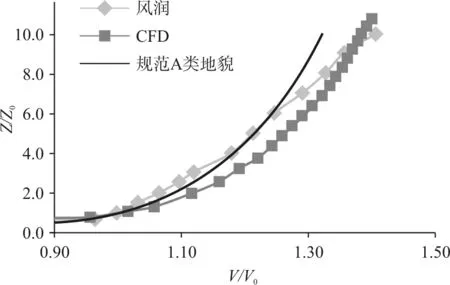
圖4 空計算域臨建筑處的平均風速剖面

2.2 孤立建筑的風壓分析

為對比試驗和模擬的結果，常對風壓系數在各屋面分區內按面積求加權均值[7]。單點風壓系數定義為：

(3)

其中P0(t)、P(t)分別為參考高度出處的總壓和靜壓，Pi(t)為測點的總壓，即為i測點在t時刻的壓力系數。在軟件中通過自定義系數設置。

為對比試驗和模擬的結果，常對風壓系數在各屋面分區內求面積加權均值[1]。圖5為CFD和風洞模擬的屋面整體平均風壓等值線對比，兩者都表現出了對稱性。圖6為單體屋面各分區平均風壓的對比，其中最大相對誤差為23 %，出現在2號區域。此為屋面上迎風的中心區域。另外根據田村幸雄[2]的做法，取迎風面、屋面和背風面中線上的風壓系數做對比，如圖7所示。其最大相對誤差出現在背風面的AH4號測點，為22%。

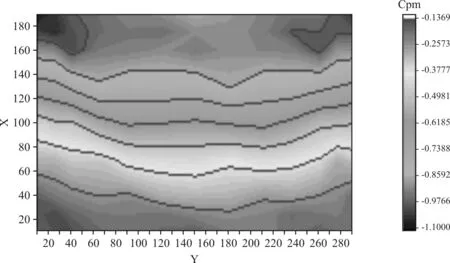
(a)平均風壓試驗值等值線

(b)平均風壓CFD模擬值圖5 屋面整體平均風壓等值線對比

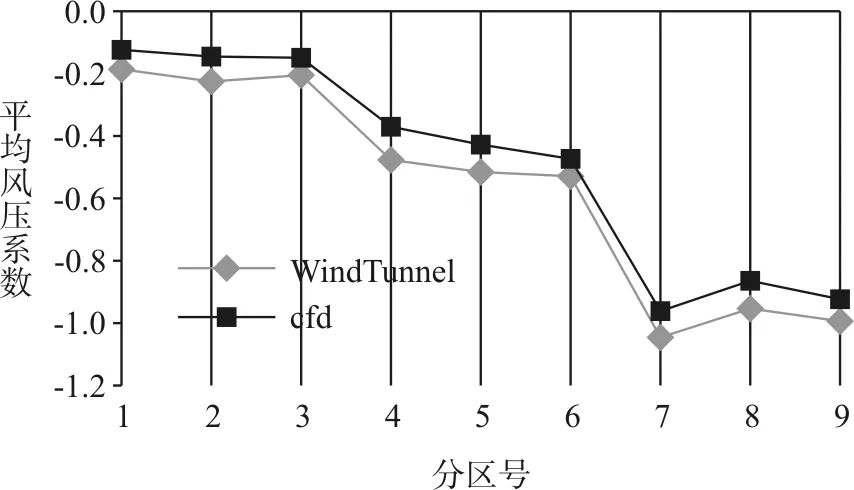
圖6 屋面各分區平均風壓對比(0°風向)

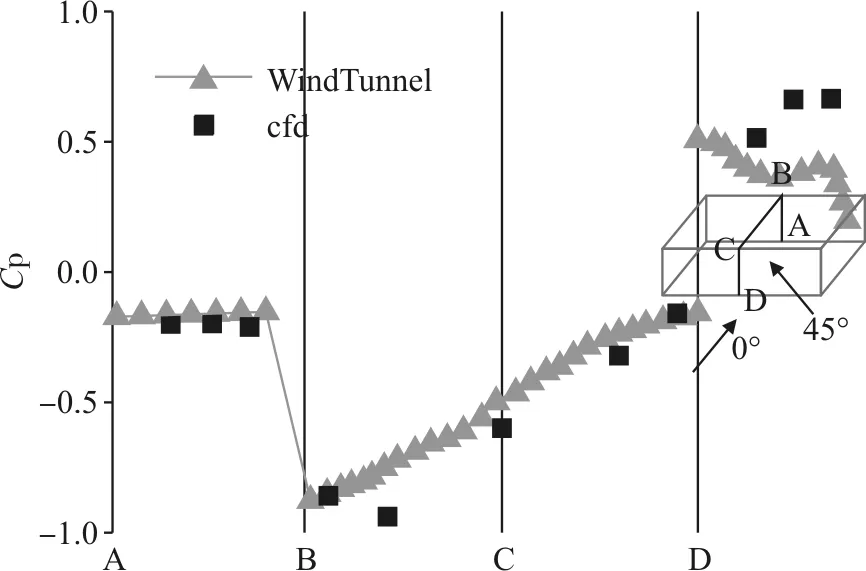
圖7 迎風面、屋面、背風面中線上的風壓系數試驗值與模擬值

2.3 結果分析

一般對力矩等風載的試驗處理方式類似高層建筑，即在模型側邊布置若干層測點，每層較為密集[6]，再結合附屬面積手動求出各向力矩。由于本試驗中模型側面的測點數較少(3層共14個)，故通過CFD模擬加以對比。Fluent提供了相對連續的各點的壓力，用于荷載的計算。表1～表3為孤立建筑的各向平均風載。另外，不同于Wonsul等[3]對各荷載系數的定義(各向荷載與該向建筑投影面積之比)，本文為了直觀起見，將參考面積統一取為1 m2。此定義應用于風洞試驗和CFD模擬的結果處理中。

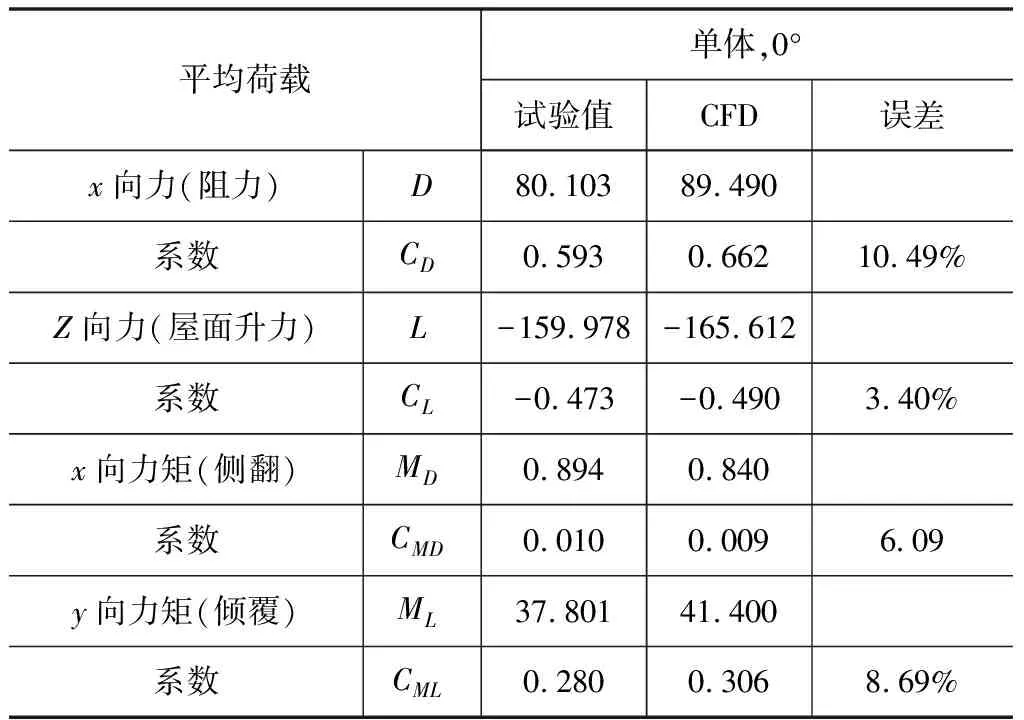
表 1 孤立建筑的表面風壓和荷載(0°)

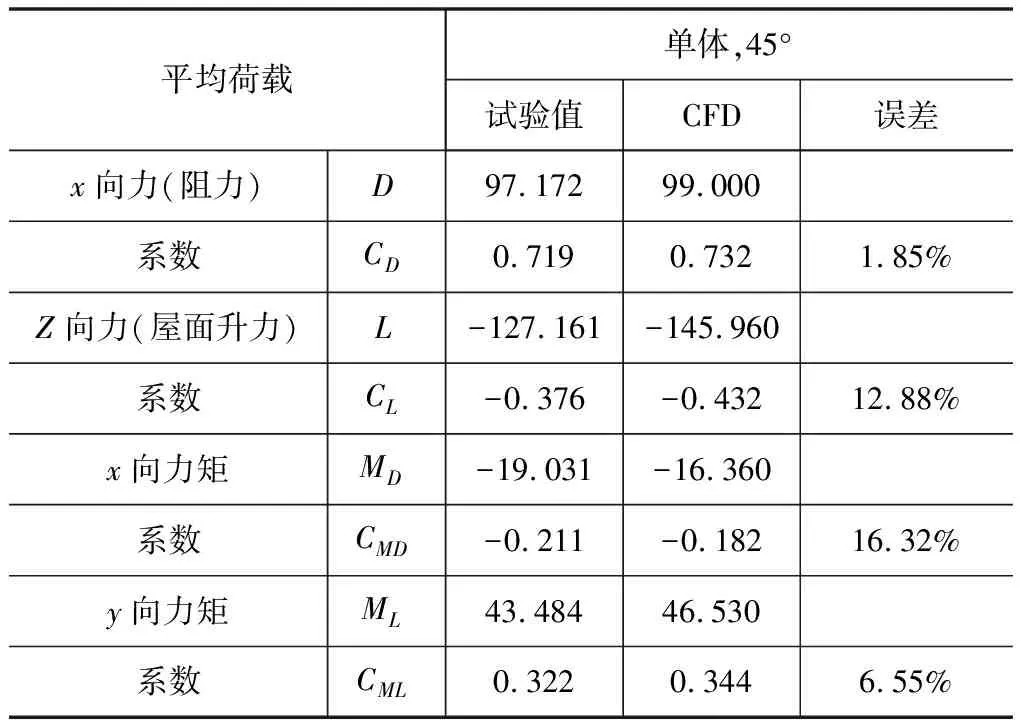
表2 孤立建筑的表面風壓和荷載(45°)

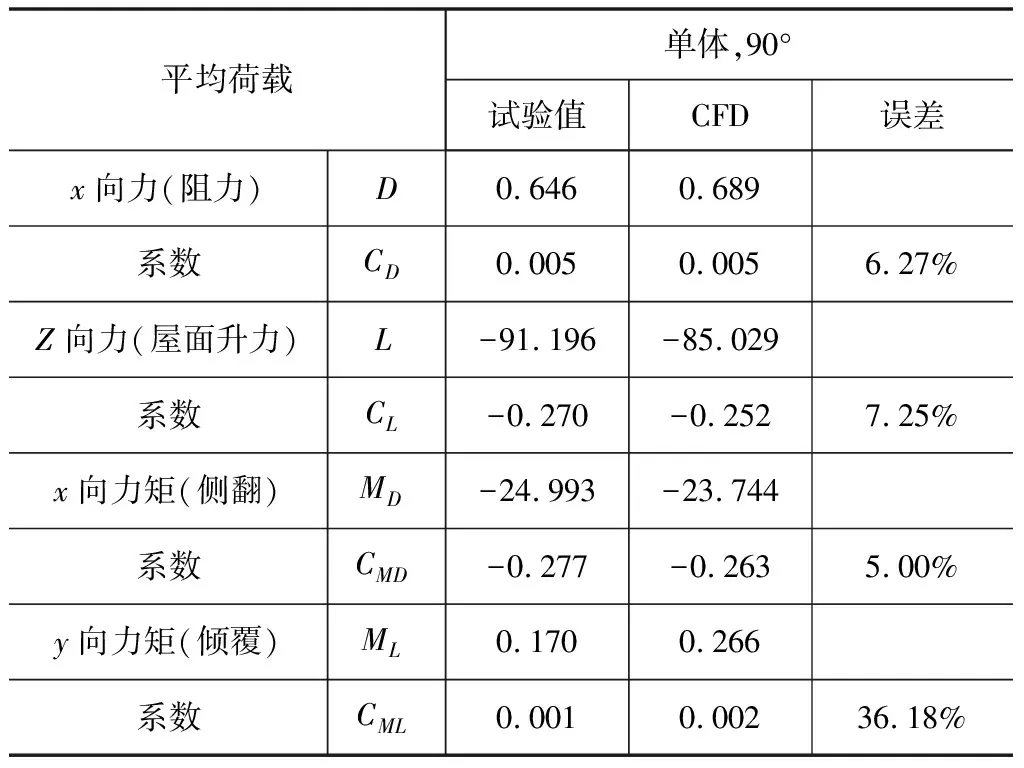
表3 孤立建筑的表面風壓和荷載(90°)

屋面負壓導致升力系數為-0.473，模擬值結果為-0.490，誤差為10.49 %；阻力系數的試驗值、模擬值分別為80.103 N、89.490 N，相對誤差為10.49 %。對稱性導致x向(側翻)力矩系數CMD接近0，試驗與模擬的相對誤差為6.09 %。y向(傾覆)力矩的試驗值與模擬值分別為分別0.280、0.306，誤差為8.69 %.90°風向下的荷載與0°風向類似。

在45°風角下，屋面升力介于0°與90°之間，為127.16 N。阻力、y向力矩均為三工況中最不利，達97.12 N、43.48 N·m。建筑表面的跡線圖如圖8所示。

圖8 t=14.0～19.0s的跡線(45°風角)

除了誤差原因在數值計算方面可能來自模擬的失真和風洞試驗中側面數據點數目的偏少。但仍可以看出對于45°風角下的建筑，對稱性的減弱加劇了建筑表面渦的脫落[5]，導致了基底荷載和增加和屋面升力的減小。

3 結論

針對典型風向下平屋蓋低矮結構的屋面風壓和基底荷載，分別進行了風洞試驗和CFD模 擬，得到以下結論：

(1)大渦模擬對平屋蓋低矮結構的屋面風壓和基底荷載的模擬誤差均在10.49 %以內，具有一定精度。

(2)45°風角下屋面風壓和基底荷載在三風角中為最不利。目前認為原因來自對稱性的減弱和屋面渦脫落的加劇。

(3)由于大渦模擬對小尺度渦的屏蔽，導致結果關于流場脈動特性的部分難以接近真實情況，即壓力和基底荷載的方差、極值、均方根誤差值都與實際存在誤差，而僅有時均值具有一定準確性。目前較少有數值算法可以解決流場的脈動特性模擬，尤其是對極值風壓系數的還原。