閥用超磁致伸縮致動器弓張結構靜、動態建模與優化

何忠波 鄭佳偉 薛光明 榮 策 柏 果

(陸軍工程大學石家莊校區車輛與電氣工程系， 石家莊 050003)

0 引言

電液伺服閥(Electro-hydraulic servo valve，EHSV)是電液伺服控制系統的核心部件。它具有控制精度高、輸出功率大、動作靈活等優點，因而在航空航天、國防工業等領域獲得了廣泛應用[1-3]。近年來，隨著電液伺服系統應用領域的不斷拓展，市場對EHSV提出了更高的性能要求，如高頻率、大流量、抗油污等，而傳統EHSV已經很難滿足上述要求[4-5]。

目前，限制EHSV發展的主要瓶頸在于先進致動器的研究。現階段用于EHSV的致動器主要包括伺服電機、力矩馬達及音圈電機等，但傳統的致動器往往不能兼具高頻響、高輸出等特性，因此在一定程度上限制了EHSV在某些動態性能要求較高的場合上的應用[6-10]。當前，基于新型功能材料的高性能致動器研究已經成為熱點，其中以超磁致伸縮材料(Giant magnetostrictive material，GMM)為驅動元件的超磁致伸縮致動器(Giant magnetostrictive actuator，GMA)因具有精度高、能量大、響應快、結構簡單等優點而備受青睞[11-13]。由于GMM磁致伸縮應變量有限，因而在研制大流量超磁致伸縮電液伺服閥時往往需為GMA加設放大機構[14-16]。目前，對于精密伺服閥用致動器，輸出位移放大方式主要有液壓放大式、懸臂梁放大式和柔性鉸鏈放大式，其中柔性鉸鏈放大式因具有位移精度高、無需潤滑、結構簡單等優點被廣泛地應用于伺服閥用致動器設計[17-22]。

本文設計一種基于柔性鉸鏈的弓張式位移放大結構，為配合閥芯的輸出方向要求，通過調整鉸鏈的分布位置，使其垂直于固定端面向外側輸出。建立弓張結構靜、動態模型，分析其結構特征參數對本身靜、動態性能的影響，在此基礎上，結合弓張放大式GMA的應用要求對其結構參數進行優化設計，以提高所設計的弓張放大式GMA的整體性能。

1 弓張放大式GMA結構及工作原理

弓張放大式GMA結構如圖1所示。基于模塊化設計思想，將弓張放大式GMA劃分為5個功能模塊，分別為預壓模塊、驅動模塊、磁致伸縮模塊、冷卻模塊及輸出模塊。預壓模塊由碟簧、前后端蓋及外殼組成，端蓋與外殼間采用螺紋連接，通過調整其間距可為GMM棒提供合適的預緊力，有利于GMA輸出特性的提升；驅動模塊由線圈骨架及線圈組成，其作用是為GMA提供驅動磁場；磁致伸縮模塊由交替排布的永磁體及GMM棒組成，該結構能提高所施加偏置磁場的均勻度，可更好地消除GMM在交變磁場下的倍頻現象，從而提高GMA的輸出特性；冷卻模塊主要由進出液口及冷卻腔組成，其作用是通過循環流動的低溫油液對整個GMA進行降溫，以保證GMM棒工作在適宜的溫度環境中；輸出模塊由弓張放大機構、輸出桿等組成，其作用是輸出GMM棒產生的伸縮變形，并將該位移進行放大，以滿足EHSV的輸入要求。

圖1 弓張放大式GMA結構圖Fig.1 Structure diagram of GMA with bow-type amplifier

整個弓張放大式GMA工作原理為：向線圈中施加驅動電流時，線圈內產生驅動磁場，GMM棒在驅動磁場和偏置磁場的作用下產生磁致伸縮微位移，該微位移通過輸出桿傳遞至弓張結構內側兩端并被放大，最終經弓張結構外側輸出端輸出。

2 弓張結構靜、動態建模

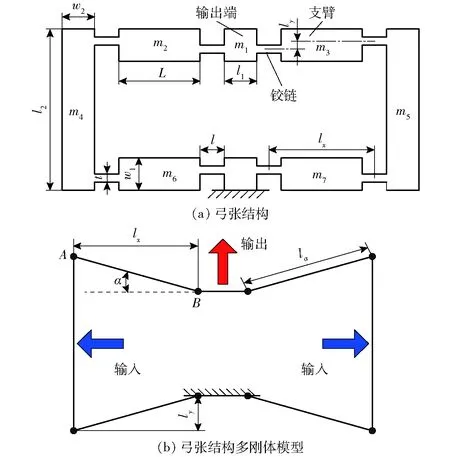
圖2 弓張結構原理圖Fig.2 Schematic diagrams of bow-type structure

用于放大GMA輸出位移的弓張結構如圖2a所示，其中m1、m2、m3、m4、m5、m6、m7分別為弓張結構各部分的質量，l、t分別為鉸鏈的長度和厚度，w1、L分別為支臂的寬度和長度，l1為輸出端的長度，l2、w2為橫梁的長度和寬度，lx、ly分別為支臂兩端的鉸鏈間的水平距離和垂直距離，α為剛體模型中支臂AB與水平方向的夾角。整個弓張結構采用整塊金屬材料經線切割制成，各支臂間采用直梁型柔性鉸鏈連接。由圖2b可知，當GMA通入電流時，弓張結構的左右兩端面產生水平方向的微位移，而輸出端則可獲得一沿豎直方向的放大位移。

2.1 靜態建模

通過分析可知，弓張結構受力彎曲的部位主要集中于柔性鉸鏈及輸入端的橫梁，考慮到弓張結構的對稱性，可取整個結構的1/4作為研究對象。分析時，將支臂近似為剛性桿，引入鉸鏈拉伸剛度Kl和彎曲剛度Kθ，弓張結構簡化后的1/4模型如圖3所示。

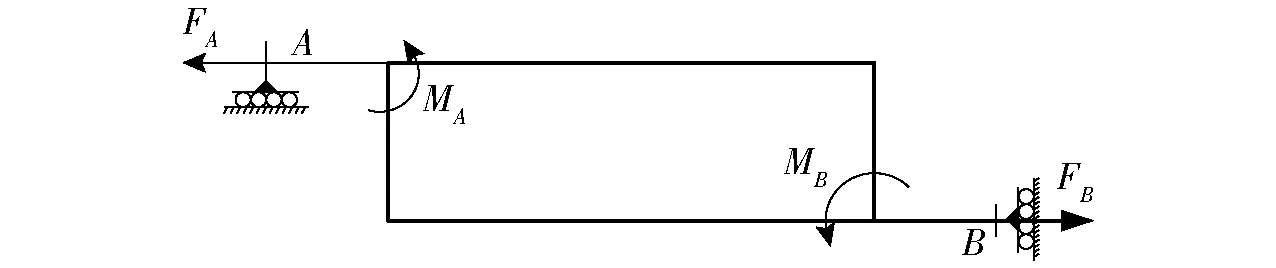
圖3 1/4模型圖Fig.3 Quarter of model

弓張機構支臂兩側分別受到水平力FA、FB的作用，該力在鉸鏈A、B處產生力矩MA、MB，由靜力平衡理論易得出

(1)

令FA=FB=F、MA=MB=M，由于鉸鏈A、B受力的狀態相同，因此二者彎曲角度相同，圖4顯示了鉸鏈A的受力彎曲狀態。

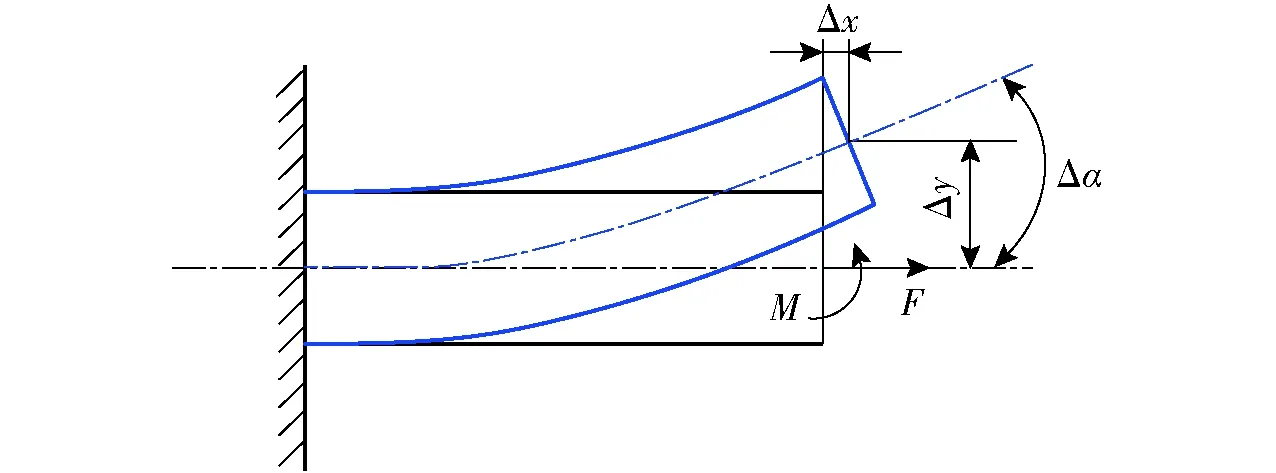
圖4 鉸鏈受力彎曲圖Fig.4 Force bending diagram of flexure hinge

基于彈性梁理論可求得

(2)

式中 Δx——鉸鏈在力F作用下產生的拉伸應變量

考慮到支臂在力矩M的作用下，所受力F的方向會發生改變及兩鉸鏈的對稱關系，因而鉸鏈實際彎曲角可表示為

(3)

鉸鏈受力彎曲后沿豎直方向的位移Δy可表示為

(4)

弓張結構兩端的橫梁可直接看作中間施加集中力的簡支梁，由材料力學知識可知，簡支梁中點處相對于其支點位移為

(5)

式中E——材料的彈性模量，Pa

b——弓張結構的厚度，mm

相對于整個機構而言，GMM棒的伸長量很小，相應的彎曲角Δα也很小，因此由支臂旋轉所產生的弦長近似等價于其弧長，由此可得1/4弓張結構在輸入力的作用下產生的水平位移dx和豎直位移dy分別為

(6)

將鉸鏈拉伸剛度Kl=Ebt/l，轉角剛度Kθ=Ebt3/(12l)的計算公式代入式(6)，最終可得整個弓張結構在輸入力F作用下產生的水平位移Dx與豎直位移Dy,分別為

(7)

結合式(6)，弓張結構的放大倍數R=Dy/Dx，可表示為

(8)

整個弓張放大式GMA的輸出位移xout可用其輸入位移(即GMA的輸出位移)xin與其放大倍數R的乘積來表示，即

xout=Rxin

(9)

根據材料力學知識及懸臂梁理論可知，放大機構受力變形時，其鉸鏈彎曲的外側面處所受最大應力為

(10)

式中W——抗彎截面系數

A——鉸鏈橫截面積，m2

2.2 動態建模

動態建模時，將整個弓張結構視作單自由度系統，根據振動理論，其固有頻率表達式為

(11)

式中Ke——弓張結構的等效剛度

Me——弓張結構的等效質量

計算弓張結構的勢能時，將柔性鉸鏈部分與支臂AB的等效剛度視為串聯，由此，弓張結構的彈性勢能可表示為

(12)

其中

式中Kα——支臂AB的等效剛度

弓張結構的動能由x、y方向的振動和繞z軸的轉動動能組成(忽略鉸鏈動能)，可以表示為

(13)

其中

ux=Dxuy=Dy

式中ux——弓張結構沿x方向的位移

uy——弓張結構沿y方向的位移

mk——弓張結構各部分質量(滿足m2=m3=m6=m7，m4=m5)

Jk——各支臂的轉動慣量，k=2，3，6，7

ω——支臂轉動角速度

將式(13)化解可得

(14)

將式(12)、(14)代入到Lagrange方程可得

(15)

式中qi——系統的廣義坐標，此處為沿y方向的位移uy

Qi(t)——系統廣義力，此處為GMA驅動力

n——系統的自由度

由式(15)可得弓張結構輸出位移的動力學微分方程為

(16)

其中

(17)

C——等效阻尼

結合式(11)、(17)，并將m1=ρl1w1b，m2=ρLw2b，m4=ρl2w2b代入可得

(18)

式中ρ——弓張結構的材料密度，kg/m3

3 弓張結構參數優化設計

考慮到所設計GMA的尺寸約束及通過對弓張結構特征參數的分析可得，弓張結構的靜、動態性能主要取決于其鉸鏈長度l、厚度t，支臂的長度L及與支臂相連兩鉸鏈間的垂直距離ly(優化前結構尺寸：t=0.60 mm、l=4.11 mm、ly=2.12 mm、L=19.90 mm)，因而主要通過分析該4個結構尺寸參數對弓張結構的影響進而對其進行結構的優化設計(其他結構尺寸分別為w1=8.00 mm，w2=10.00 mm，l1=10.00 mm，l2=45.00 mm，b=10.00 mm)。

3.1 靜態分析

由式(9)可知，當GMA輸入位移xin一定時，弓張放大式GMA的最終輸出位移xout主要取決于弓張結構的放大比R。通過Matlab軟件對放大比R進行分析，結果如圖5所示。

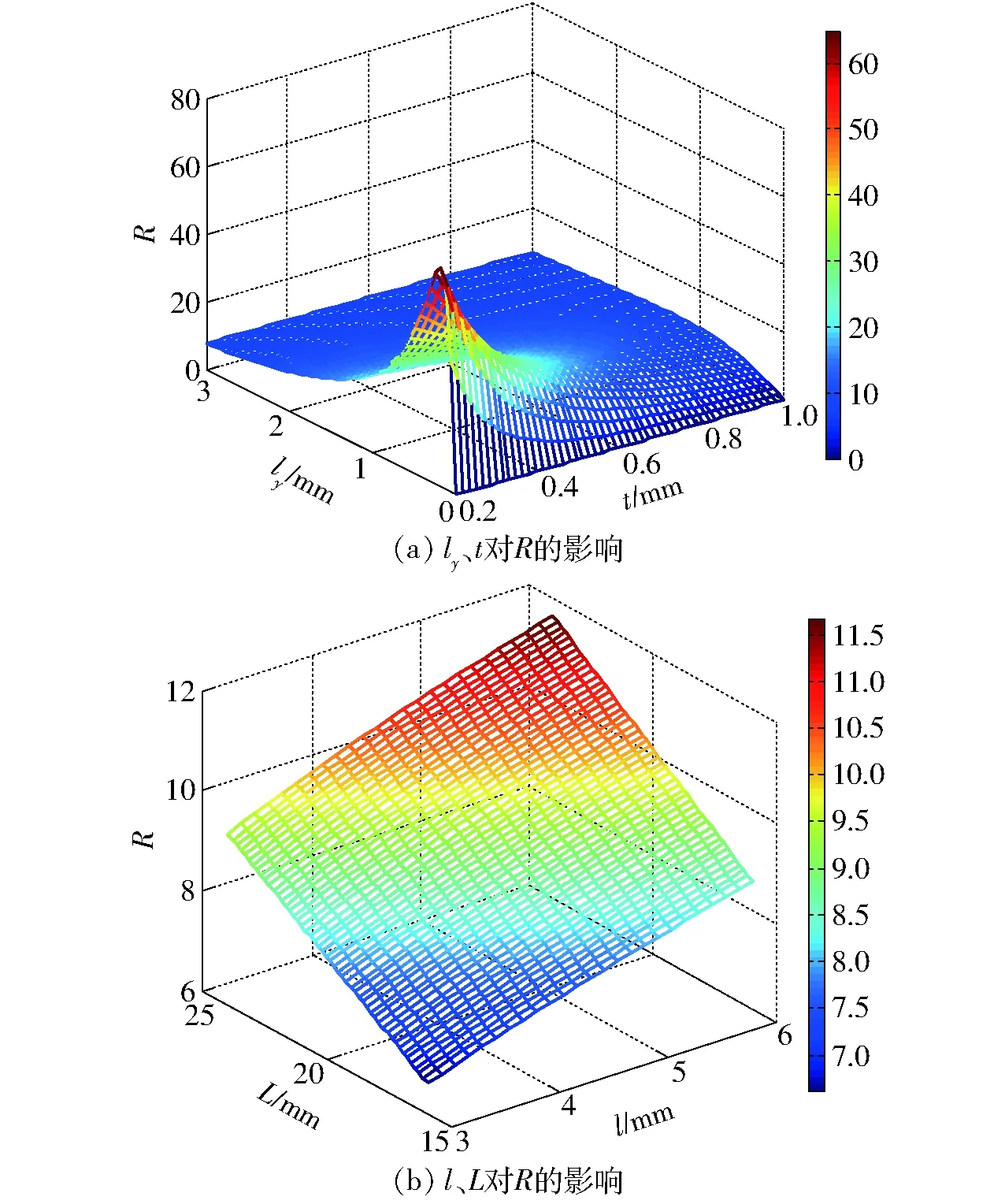
圖5 各尺寸參數對R的影響Fig.5 Effects of each dimensional parameter on R

由圖5a可知，鉸鏈厚度t、相鄰鉸鏈間垂直距離ly與放大比R均呈現出非線性關系，當t∈[0.2 mm，0.4 mm]時，放大比R隨t的增大急劇減小，當t大于0.4 mm時，放大比R下降減緩；而隨著ly增大，放大比R則先急劇增大到最值后逐漸減小。由圖5b可知，鉸鏈長度l、支臂長度L與放大比R間表現為正相關，即隨著l、L增大，放大比R逐漸增大。

3.2 動態分析

通過式(18)可知支臂長度L、相鄰鉸鏈間垂直距離ly、鉸鏈厚度t及長度l對弓張結構的固有頻率的影響，其結果如圖6所示。

圖6 各尺寸參數對fn的影響Fig.6 Effects of each dimensional parameter on fn

由圖6a可知，隨著鉸鏈厚度t增大，固有頻率fn亦增大，而隨著相鄰鉸鏈間垂直距離ly增大，fn先急劇增大到最值后出現極小幅度的減小；由圖6b可知，鉸鏈長度l、支臂長度L與固有頻率fn間表現為負相關，即隨著l、L增大，固有頻率fn逐漸減小。

3.3 優化設計

考慮到優化設計時涉及到靜、動態性能的2個指標，因而選用可進行多目標優化的gamultiobj函數對弓張結構進行設計。該方法基于遺傳算法，相對于其他數值優化算法，具有更好的魯棒性和尋優能力，能夠高效地獲取最優解。

通過上述對弓張結構靜、動態分析可知，要提高其輸出位移量，需增大鉸鏈長度l、支臂長度L或減小鉸鏈厚度t，而要提高其固有頻率，則需減小鉸鏈長度l、支臂長度L或增大鉸鏈厚度t。由此可知，弓張結構的靜、動態性能是相互制約的。因而需對弓張結構的特征參數t、l、ly、L進行優化，合理設計該參數取值，使得弓張結構的靜、動態性能達到最優。令t=x1、l=x2、ly=x3、L=x4、1/Dy=f1(x)、1/fn=f2(x)，由此建立弓張結構的雙目標函數為(考慮到fn的算式較復雜，計算時，忽略Δz對fn的影響)

(19)

由于所設計GMA結構尺寸參數已確定，同時為避免弓張結構的靜、動態性能差異過大，因而設定目標函數的線性約束條件為：0.6 mm≤t≤1.2 mm，3.5 mm≤l≤5.0 mm，1.6 mm≤ly≤2.6 mm，19.0 mm≤L≤22.0 mm。

目標函數的非線性約束條件包括：

(1)考慮到所設計弓張式GMA用于伺服閥閥芯的驅動，因而其輸出位移需滿足閥的性能要求，由于GMA的輸出位移一定，因此弓張結構的放大比R需滿足8≤R≤10。

(2)弓張放大式GMA驅動閥芯工作還需滿足驅動力(弓張放大式GMA的輸出力Fout)要求。弓張放大式GMA的輸出力與其輸入力Fin(GMA的輸出力)之間滿足Fin≈RFout，而GMA的輸出力即Fin=Kindx，因此弓張結構的輸入剛度需滿足2.5×107N/m≤Kin≤3.2×107N/m。

(3)弓張結構的固有頻率fn會限制所設計伺服閥的響應頻寬，因而要求其fn滿足fn≥150 Hz。

(4)當弓張結構發生變形時，其鉸鏈外側面所承受的最大應力σmax滿足σmax≤[σ]。

(20)

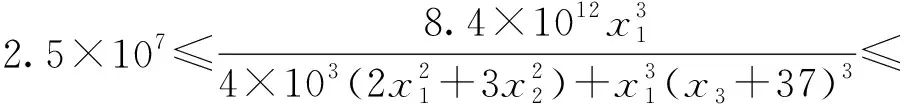
(21)

(22)

(23)

利用Matlab對gamultiobj函數進行調用。該遺傳算法中，種群大小關系到全局尋獲最優解及尋優運行時間長短，綜合考慮，此處設置為100；為獲取30個最優解以便于最終優化結果的篩選，最優前端個體系數設置為0.3；最大進化代數(算法最大迭代次數)設置為200，停止代數也為200，適應度函數值偏差為1×10-100，使得算法能在進化200代后停止。繪制算法運行后獲取的Pareto前端個體分布如圖7所示。

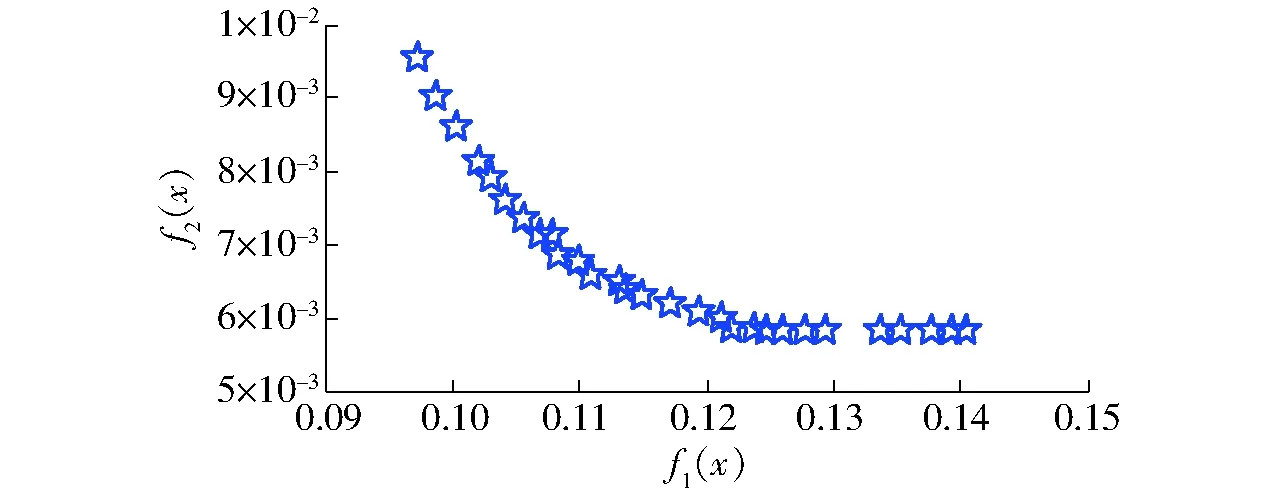
圖7 Pareto前端個體分布圖Fig.7 Distribution diagram of Pareto front

通過Matlab獲取gamultiobj函數的Pareto解集，整個優化過程如圖8所示。

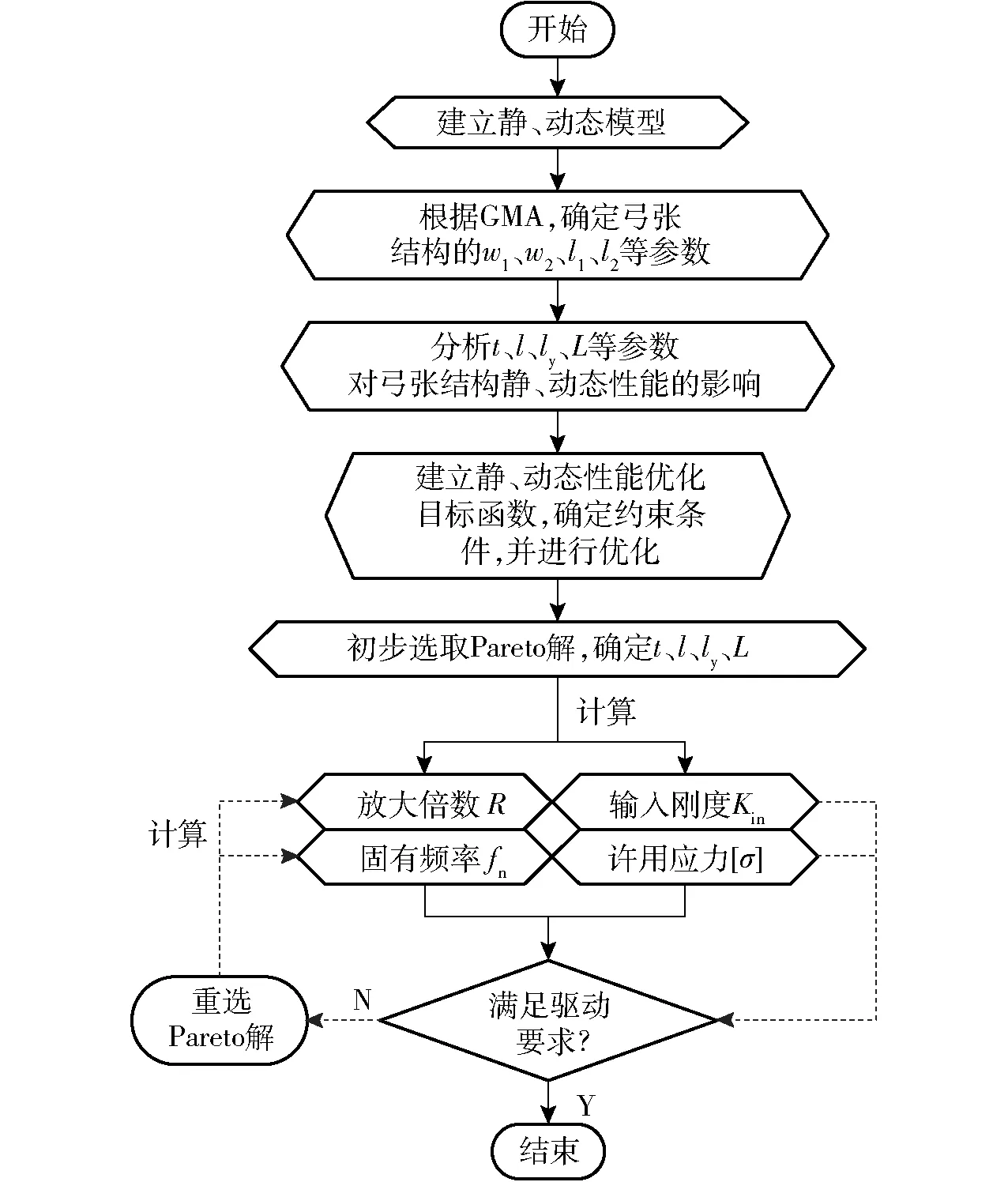
圖8 優化流程圖Fig.8 Flowchart of optimization

最終確定優化結果為：t=0.9 mm、l=4.2 mm、ly=2.0 mm、L=20.0 mm，并由此得出弓張結構的輸出位移Dy=8.96Dx，固有頻率fn=179.1 Hz。

4 仿真及實驗

為驗證弓張結構靜、動態模型建立的正確性，使用有限元軟件對其進行仿真分析。弓張結構材料選用合金彈簧鋼(65Si2Mn)，彈性模量E=210 GPa，密度為ρ=7 850 kg/m3，屈服極限為1 176 MPa，許用應力[σ]為780 MPa，泊松比為0.28。

4.1 靜態仿真

分析時將橫向位移輸出端面的對應面設為固定約束，其他面均為自由，在兩側軸向輸入的內端面的中心局部面積上施加均布力。弓張結構的相對位移及應力分布如圖9所示。

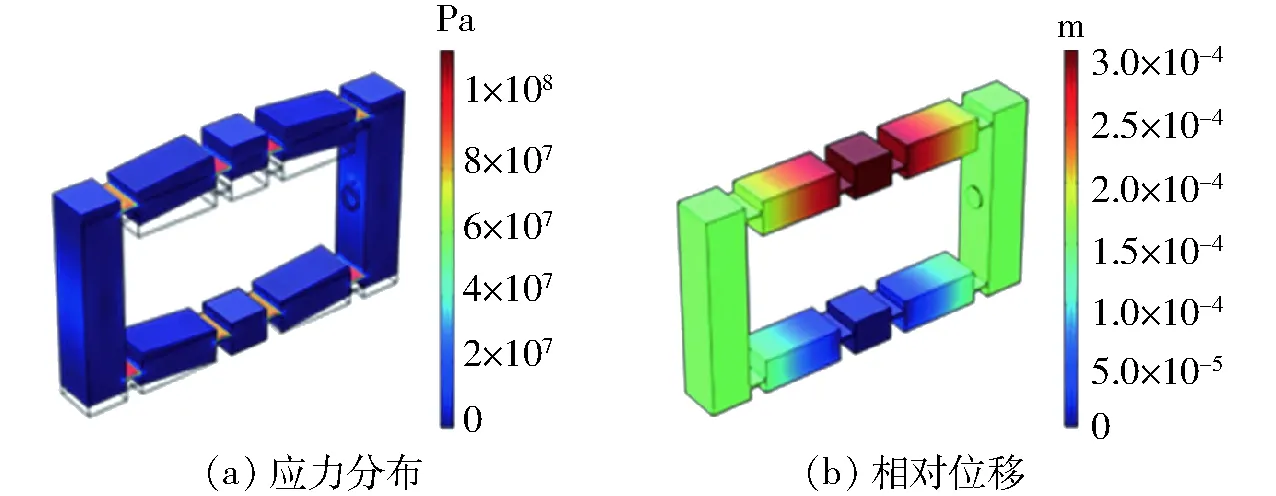
圖9 有限元分析圖Fig.9 Diagrams of finite element analysis

通過施加0～800 N的均布力，經仿真得到弓張結構輸入、輸出位移量與理論計算得到輸入、輸出位移量關系，如圖10所示。

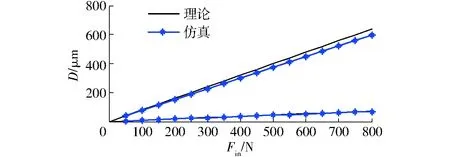
圖10 輸入與輸出關系曲線Fig.10 Relationship curves of input and output

由圖10可知，經有限元分析得到的輸入、輸出位移量與理論計算所得結果基本吻合，說明所建立模型正確；同時觀察到仿真結果隨著輸入均布力的增加呈線性關系，由此可得在弓張結構各尺寸參數確定的條件下，其放大倍數及靜態等效剛度基本不變。經數據處理得，仿真分析所得弓張結構的放大倍數R在8.50～8.68之間，理論分析得R=8.96，相對誤差為3.1%～5.1%。

4.2 動態仿真

弓張結構的動態仿真主要是對其進行模態分析，通過有限元軟件對其進行特征頻率研究，振型階數設置為4，頻率間隔設置為1 Hz，得其前4階模態及諧振頻率如圖11所示。

圖11 弓張結構模態分析Fig.11 Modal analysis of bow-type structure

由圖11可知，弓張結構的2階模態振型與其單自由度模型的振動方式相同，而其他階次的振型會引起位移輸出端的側向振動。利用有限元仿真得到弓張結構的2階振型的頻率為196.8 Hz，對比動力學分析得到的固有頻率179.1 Hz，兩者間誤差為8.9%，說明模型計算結果與有限元仿真結果基本吻合。

4.3 靜、動態實驗

為驗證上文靜、動態分析及有限元分析的正確性，按照優化設計后參數加工制作了弓張放大式GMA實驗樣機，并搭建了實驗測試系統，如圖12、13所示。

圖12 弓張結構及GMA樣機Fig.12 Prototype of bow-type structure and GMA

圖13 實驗系統組成圖Fig.13 Photo of experimental system1.冷卻機構 2.Microtrak 3-LTS-025-02型激光位移傳感器 3.pico-TA189型電流鉗 4.弓張放大式GMA樣機 5.Rigol-DS1074Z型數字示波器 6.IT6932A型可編程電壓源 7.Rigol-DG1022U型信號發生器 8.GF800型功率放大器

4.3.1靜態實驗

弓張放大式GMA的靜態性能測試可通過其對不同幅值的直流電流信號的響應曲線獲取。即分別向線圈中通入幅值為±1、±2、±3、±4、±5 A的直流電流，實驗時，每個幅值對應位移量測量10次，數據處理時取平均值，最終得到弓張式GMA的輸入、輸出位移，如圖14所示。

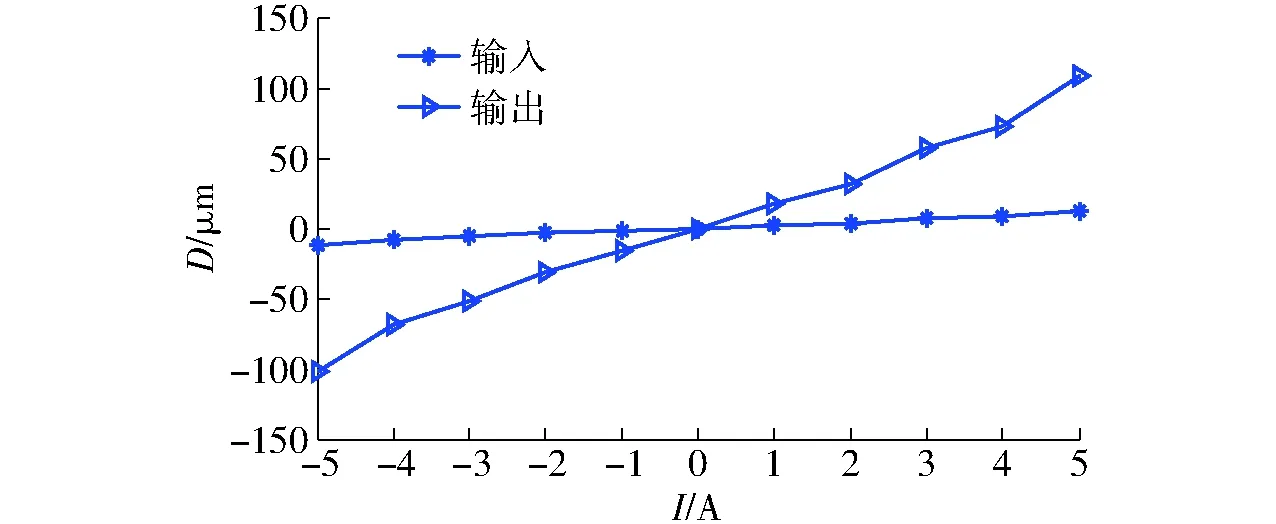
圖14 靜態響應曲線Fig.14 Curves of static response

經數據處理可知，靜態實驗測得弓張結構放大倍數在8.13～8.72之間，最大輸出位移可達107.9 μm，與理論計算所得值間的相對誤差為2.7%～9.2%，其中最大誤差出現在驅動電流為-4 A時，誤差約為7.1 μm。

4.3.2動態實驗

弓張放大式GMA的動態性能的測試可通過其對不同頻率的正弦電流信號的響應曲線獲取，即通過掃頻實驗以探究弓張結構的固有頻率。設置電流幅值為3 A，頻率范圍為0～200 Hz，掃頻時間為1 s，各頻率停留時間均等，其時域檢測結果如圖15所示。

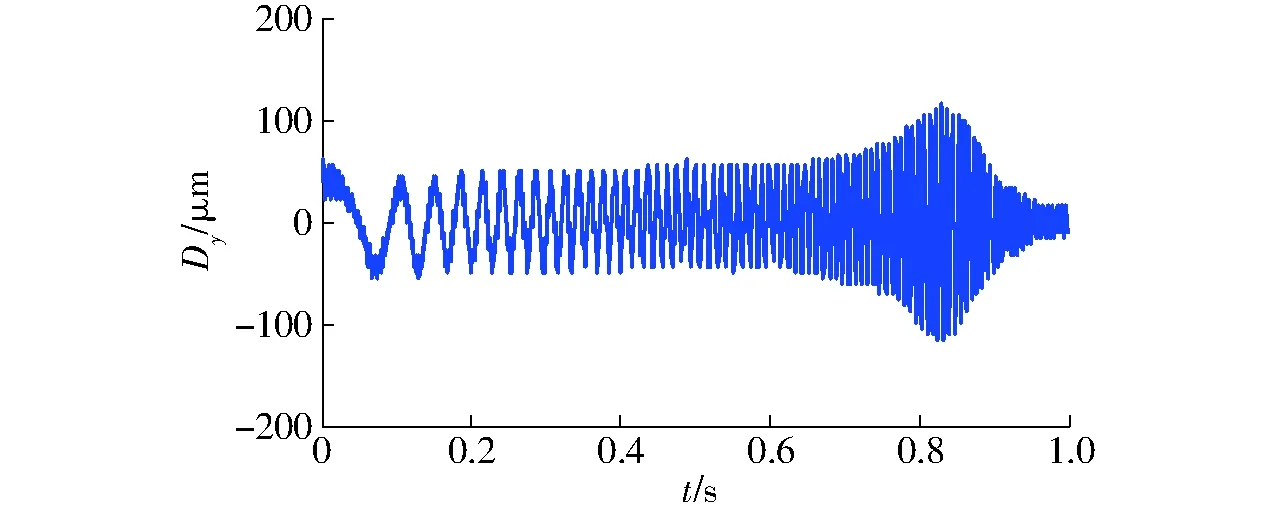
圖15 動態響應曲線Fig.15 Curve of dynamic response

由數據分析可得，弓張結構輸出位移在168 Hz處達到峰值，此處掃描頻率導致其產生結構諧振，即實驗所得固有頻率為168 Hz，與理論計算值間相對誤差為6.2%。同時由圖15可知，當掃描頻率小于168 Hz時，其輸出位移較為穩定；當掃描頻率超過168 Hz時，其輸出位移急劇減小。說明當輸入電流頻率超過168 Hz時，弓張放大式GMA輸出性能較差，其原因可能是高頻條件，GMA內部驅動線圈阻抗增大，影響了其輸出特性。

4.3.3優化前后性能對比

經優化后所得弓張結構靜、動態性能理論、仿真、實驗結果與優化前結果對比如表1所示。

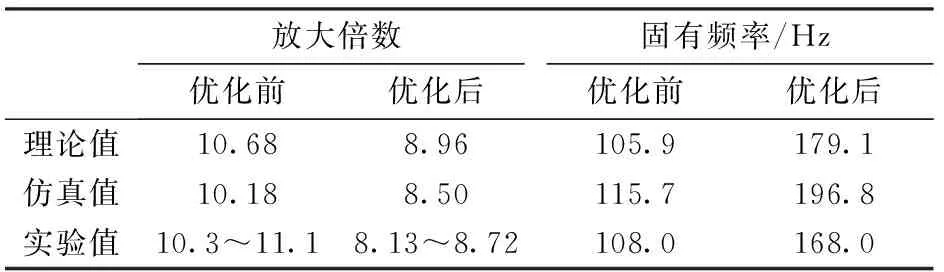
表1 優化前后性能對比Tab.1 Optimized performance comparison

由表1可知，弓張結構在靜態放大倍數滿足伺服閥驅動要求的條件下，固有頻率由108 Hz增大到168 Hz，動態性能提高了55.6%，說明了該優化設計方法的有效性。

5 結論

(1)設計了一種體積小、結構緊湊的弓張放大式GMA，能夠較好地放大GMA的輸出位移。

(2)基于理論力學、材料力學及振動理論等知識建立了弓張結構靜、動態模型，并通過Matlab分析了弓張結構主要尺寸參數對其靜、動態性能的影響，結果表明其靜、動態性能是相互制約的。

(3)利用可進行多目標優化的gamultiobj函數對弓張結構的靜、動態性能進行設計，確定了其結構尺寸參數，并利用有限元法對其靜、動態性能進行仿真分析，仿真結果與理論計算值相吻合。

(4)針對弓張結構靜、動態模型分析，搭建了相關實驗測試系統，靜態實驗測得其放大倍數在8.13～8.72之間，最大輸出位移可達107.9 μm；動態實驗測試得其固有頻率為168 Hz，對比于優化前，提高了55.6%；結果表明測試所得與靜、動態模型計算值相符，弓張結構靜、動態性能基本能滿足伺服閥驅動要求，證明了該優化設計方法的有效性。