加工中心床身尺寸元結構方法的優化研究

李 強

（遼寧軌道交通職業學院 科技實訓中心，遼寧 沈陽 110023）

1 引言

隨著科學技術的快速發展，高檔數控機床正向高速度、高精度、高效率、復合化方向發展。床身是數控機床的關鍵基礎支撐件，而且床身的結構尺寸及重量較大，其本身的靜動剛度、抗震性以及熱穩定性直接影響到整機的工作性能[1-2]。所以對床身尺寸優化能很好的節省材料，進而提高床身的使用性能，會給機床廠家帶來可觀的經濟效益。但是由于床身結構復雜，因此考慮以構成機床床身的內部結構為出發點，引入元結構的基本概念來對床身尺寸進行優化，其中元結構的基本思想就是把機床床身組成的形體進行分解，最終可以分解得到一些基本的單元結構[3-4]。文獻[5]在理論模型基礎上對機床床身進行靜力學分析和動力學分析；文獻[6]從加工工藝角度對機床結構性能分析，尤其與機床連接部分對結構影響分析，具有一定研究意義；文獻[7-8]考慮機床結構對整機動態特性影響進行有效分析，采用有限元方法進行優化設計。另外床身結構將直接影響床身幾何精度，比如床身本身結構及性能，床身安裝牢固；床頭箱與床身連接，臥式機床尾座與床身連接、床身上導軌幾何精度及與滑鞍運動精度關系，及其保持性等等[9-10]。

2 典型筋格結構的選擇及類型

加工中心機床床身內部筋格單元結構尺寸有大有小，位置有高有低，筋格壁板有厚有薄，對機床每一筋格進行尺寸優化顯然不現實，因此，對筋格進行分類和把具有典型代表結構的筋格篩選出來顯得非常必要。將床身內數量大、出砂孔布置類型相同（X、Y方向出砂孔呈圓形，Z方向出砂孔呈方形）的六面體六出砂孔筋格單元看作是典型筋格結構。這類典型筋格結構形狀規則，數量大，分析計算容易，其機械性能可以代表床身大部分筋格的機械性能，是理想的尺寸結構優化對象。床身內部筋格數量眾多、尺寸各異、位置不同。為了之后進行類別劃分，我們要對眾多筋格進行筋格編號。參考筋格編號，如圖1所示。

圖1 床身筋格結構編號圖Fig.1 Bed Rib Structure Number Map

具體編號方法如下：筋格編號：（X；Y；Z），其中 X、Y、Z=1，2，3…。例如筋格編號為（2；3；2）時，表示X坐標編號為2，Y坐標編號為3，Z坐標編號為2的筋格。加工中心床身包括兩種類型的典型筋格單元結構，其坐標編號分為（4；3；1）和（4；2；1），分別稱作第一類典型筋格結構和第二類典型筋格結構。選這兩個筋格作為典型筋格結構，有兩種原因：1、此兩筋格在X、Y、Z方向尺寸上具有代表性，能代表該床身大部分規則筋格結構（六面體，六個出砂孔）；2、為以后進行兩筋格聯合體研究方便，使筋格坐標編號的X、Z方向編號值相同。

3 加工中心床身的模態分析

機械結構的低階頻率，對評估結構的振動情況具有更重要的價值，在機床實際工作過程中的工作頻率，尤其是考慮一階固有頻率，這樣能盡可能的避免共振現象的發生。在此HNC系列加工中心模態分析采用ANSYS有限元軟件中的Block Lanczos法進行計算分析，計算前四階的模態。振型圖，如圖2所示。經分析圖2中一階模態振型為立柱側的床身沿Y方向上下擺動；二階模態振型為沿Z方向前后擺動；三階模態振型為在XOZ平面內床身整體發生扭曲變形；四階模態振型為在XOZ平面內床身整體發生扭曲變形。

圖2 床身模態分析振型圖Fig.2 The Modal Analysis of Vibration Map

4 機床床身結構的優化分析

在加工中心床身模態分析基礎，對其進行必要的優化分析。以床身局部進行設計：其尺寸分別為：L=315mm，W=345mm，H=240mm，d1=d2=100mm，a=b=90mm，t=20mm。

式中：d1—XZ面圓形出砂孔直徑；d2—YZ面圓形出砂孔直徑，l0、w0—XY面內方形出砂孔的長和寬；t—筋格壁厚（即床身內部筋板厚度）；L、W、H—筋格的長、寬、高；a、b—XZ 面內方形出砂孔邊緣距筋格邊緣的距離。

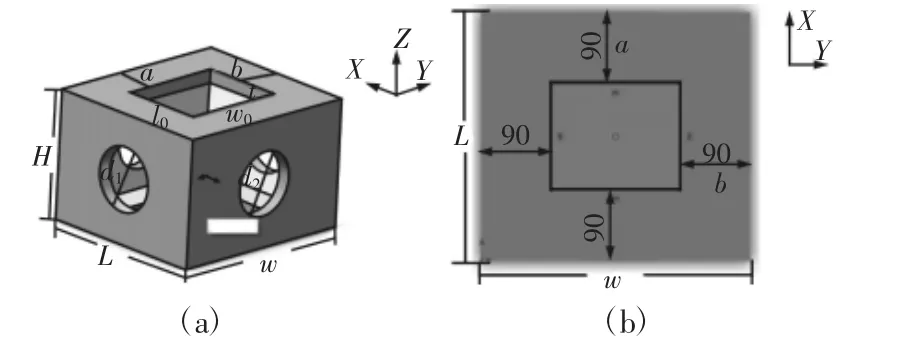
圖3 第一類典型筋格三維模型及原典型筋格上下方孔尺寸Fig.3 Three Dimensional Model of the First Kind of Typical Lattice and the Pore Size of the Original Typical Bar

經過測算對比，發現典型的筋格結構中疑似不盡合理的尺寸：筋格側壁圓孔直徑和上下方形出砂孔尺寸。對于筋格側壁圓孔尺寸，如圖3（a）所示。筋格長L、寬W、高H各不相等，甚至相差較大的情況下，出砂孔圓孔尺寸d1=d2，即筋格側壁尺寸不等，兩個方向的側壁的圓形出砂孔尺寸卻相等。相應對策是調整XZ面和YZ面內出砂孔直徑至各面內最優值。如圖3（b）所示，對于筋格上下方孔，筋格X、Y方向尺寸不等，但方孔邊到筋格邊寬度a、b，卻都是90mm，該種設計導致了方孔對筋格X、Y方向的性能影響不一致。相應對策是分別改變方孔X、Y方向尺寸，使方孔沿個方向性能印象趨向一致且到最優值。該典型筋格結構的優化分析思路如下：（1）其他尺寸不變，改變d1/H比值，并進行模態分析，使筋格低階振頻較原筋格達到較優值；（2）在第一步優化基礎上，控制其他尺寸不變，改變d2/H比值，并進行模態分析，使筋格低階振頻較第一步優化筋格達到較優值；（3）在第二步優化基礎上，控制其他尺寸不變，改變l0/L比值或w0/W比值（保證l0/L=w0/W），并進行模態分析，使筋格低階振頻較第二步優化筋格達到較優值；（4）在第三步優化結果的基礎上改變肋板厚度，并進行模態分析，使筋格低階振頻較第三步優化筋格的低階頻率達到較優值，并將第四步優化筋格作為筋格的最終尺寸優化方案，從而實現原筋格典型結構的尺寸優化。床身原筋格元結構前六階固有頻率，如表1所示。

表1 原筋格元結構前六階固有頻率（Hz）Tab.1 Order Natural Frequency（Hz）of the Original Lattice Structure

4.1 改變d1/H比值

如上所述，筋格高H=240mm，原筋格d1/H=100/240=0.42改變d1/H比值，并對比值改變過程中相應筋格進行模態分析，根據模態分析結果得到筋格前三階固有頻率變化曲線，如圖4所示。

圖4 XZ面變圓固有頻率變化曲線Fig.4 The Curve of the Natural Frequency of the XZ Plane

通過分析曲線可知，取d1/H=0.4，即d1=96mm時，筋格結構有較高的低階固有頻率和較大的出砂孔尺寸，為了鑄造工藝安排方便，取整后讓d1=100mm，即原筋格XZ面內的圓形出砂孔尺寸已經比較合理，該面內出砂孔尺寸不用修改。

4.2 改變d2/H比值

筋格高H=240mm，原筋格d2/H=100/240=0.42改變d2/H比值，并對比值改變過程中相應筋格進行模態分析，根據模態分析結果得到筋格前三階固有頻率變化曲線，如圖5所示。根據圖5所示的筋格YZ面內出砂孔固有頻率變化曲線，我們可以看出d2/H在（0.4～0.5）之間取值時，即 d2在（96～120）mm 之間取值時，可以使改進筋格結構有更高的低階固有頻率和更大的出砂孔尺寸，二原筋格d2=100mm的尺寸較為保守，將d2改為d2=110mm。改進以后的筋格元結構與原筋格結構相比有更大的方形出砂孔尺寸，且低階固有頻率沒有大幅變小，甚至一階固有頻率有所升高，改善后的筋格數據，如表2所示。可見，適當增大d2尺寸，有利于筋格減重和動態性能的改善。從表2可以看出，一階、五階、六階固有頻率有不同程度的升高，二階、三階、四階則由小幅回落。我們知道，低階固有頻率中，一階固有頻率最能反映床身的動態性能，因此我們認為改進筋格（暫記為“改1”）與原筋格相比YZ出砂孔尺寸變大，質量減小，且動態性能升高。

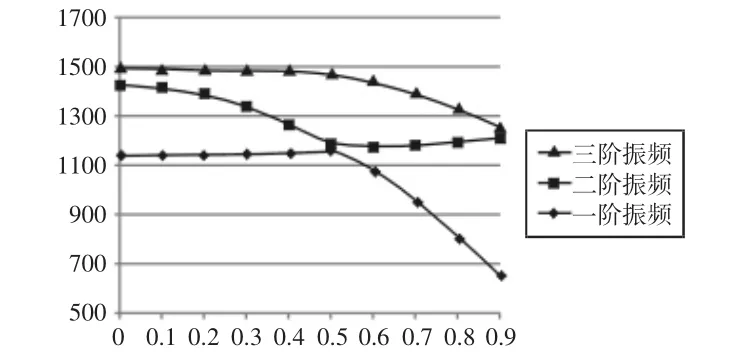
圖5 前后變圓固有頻率變化曲線Fig.5 Variation Curve of the Natural Frequency of the Circle

表2 改進筋格結構低階固有頻率（Hz）Tab.2 The Low Order Natural Frequency（Hz）of the Improved Lattice Structure

4.3 改變l0/L比值（或w0/W比值）

原筋格結構尺寸中，XY面內方孔長邊距筋格長邊a=90mm，方孔短邊距筋格短邊b=90mm，即l0/L=0.48，w0/W=0.43，即l0/L≠w0/W。這種筋格邊長各不相等而出砂孔距筋格邊尺寸相等的設計，容易導致出砂孔對筋格不同方向機械性能影響不一致，而且容易出現局部性能不足或局部性能過剩的情形。改變方孔l0/L比值或w0/W比值（保證l0/L=w0/W），并進行相應的模態分析，根據模態分析結果得到筋格前三階固有頻率變化曲線，如圖6所示。

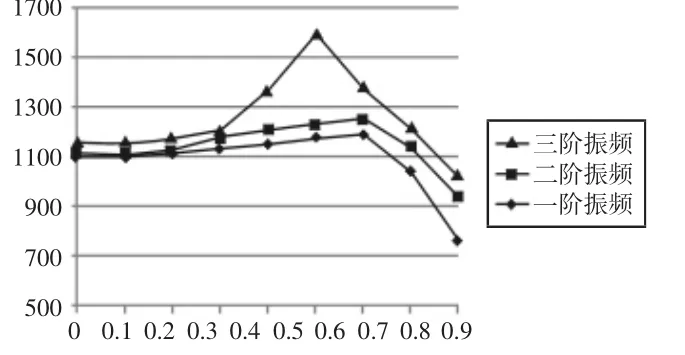
圖6 上下變量方孔固有頻率變化曲線Fig.6 The Natural Frequency Variation Curve of the Upper and Lower Variables Square Holes

從圖6中可以看出，l0/L=w0/W在0.5和0.6之間取值時，與原筋格相比，改進筋格元結構有更高的低階固有頻率和更大的出砂孔尺寸。在筋格優化設計中，為了盡可能減小對筋格靜態性能的影響，在增大出砂孔尺寸的同時，去相對保守的比值，取l0/L=w0/W=0.5，得 l0=157.5，w0=172.5，圓整后有 l0=155，w0=170。筋格 XZ 面方孔優化后，方孔優化前后尺寸和前六階固有頻率，如表3所示。

表3 方孔優化前后尺寸及前六階固有頻率Tab.3 Dimensions and the Six Natural Frequency of Square Holes Before and After Optimization

XY面方形孔面積有明顯增加；一、三階振頻有不同程度的改善，二階振頻有一定程度的下降。但低階振頻中一階振頻比二階振頻對筋格固有頻率的影響更大，因此，認為筋格改進模型動態性能得到改善。該類型筋格在質量減小的情況下，動態性能得到改善，即筋格的尺寸優化是有效的。

5 結論

（1）筋格典型結構組成的筋格二元聯合體修改前后，在質量上下降3.69%的情況下，前四階振頻分別有不同程度的提高，筋格聯合體性能得到改善。（2）各階振頻的大小不隨筋格質量的大小而變化，而與具體的筋格結構相關；另外筋格聯合體各階振頻介于構成其的兩單個筋格相應振頻之間。（3）通過有效優化設計分析，在加工中心床身結構質量減小的情況下，動態性能得到改善，即筋格的尺寸優化是有效的。