直升機載ROSAR運動補償及成像算法

，

(1.中國電子科技集團公司第三十八研究所， 安徽合肥 230088；2.重慶大學飛行器通信與測控中心教育部重點實驗室， 重慶 400044)

0 引言

隨著我國通用航空快速發展，低空使用逐步開放，低空空域環境日益復雜。能夠在低空復雜空域環境和不良氣候條件下，對威脅物精確探測和實時感知是保證飛行器尤其是大規模救援情況下多飛行器的安全飛行、提高航空應急救援效率的前提。直升機是迄今為止機動性最優的一種空中平臺，可以垂直起降、貼地飛行，可以在未經平整的地點著陸，甚至可以在空中懸停或者占領某一據點。因此，直升機平臺是災區大規模救援和空中作戰的理想平臺，而目前軍民兩用直升機的飛行能力主要受限于氣候條件。如果缺乏可靠的飛行路徑和著陸地點障礙物探測感知手段，在復雜低空空域環境下直升機安全會受到嚴重威脅。

直升機載旋轉式合成孔徑雷達(ROSAR)[1-4]天線安裝在直升機旋翼葉片的端部或在一個高于旋翼的剛性支架上，利用天線隨旋翼的旋轉運動來合成方位向孔徑，而無需平臺的運動，就能夠得到對航線周圍場景的高分辨圖像來實現目標探測和定位。已有的直升機載ROSAR成像算法[2-5]要求在成像過程中平臺處于懸停靜止狀態，然而在實際工作環境中，直升機平臺不可能完全處于靜止狀態，平臺的運動將會導致現有的直升機載ROSAR成像算法失效。因此，如何在直升機運動情況下得到聚焦良好的ROSAR成像結果是需要進一步深入研究的問題，這也更符合直升機在飛行和降落過程中感知周圍環境的實際需要。

針對上述問題，本文提出一種融合直升機平臺運動補償的改進的Chirp Scaling(CS)算法。本文首先建立了存在平臺運動時直升機載ROSAR成像的幾何模型，在此基礎上，對平臺運動引起的目標斜距誤差在合成孔徑時間內隨目標斜距的變化關系進行了詳細的分析，得到了平臺運動引入的斜距誤差的空變特性，并給出了誤差補償方法。然后針對直升機載ROSAR幾何構型的特殊性，分析了雷達相位中心等效速度隨場景目標斜距變化特性對成像質量影響，并在CS算法的距離徙動空變性校正和方位壓縮過程中補償該影響。所提方法只包含FFT和復乘運算，不涉及插值操作，易于工程實現。理論分析和仿真實驗結果表明，該算法能夠在直升機平臺存在運動時，有效實現對大場景的成像。

1 直升機平臺運動的ROSAR信號模型

傳統的直升機載ROSAR成像算法針對直升機平臺處于懸停靜止狀態，其觀測幾何示意圖如圖1(a)所示。雷達天線安裝在旋翼葉片端部，隨旋翼葉片的旋轉，在地面上形成內徑為r1，中心半徑為r0，外徑為r2的圓環型成像區域，區域大小取決于載機高度H、天線俯仰向波束寬度ε和下視角φ。天線相位中心在z=H的平面內以(0,0,H)點為圓心，旋翼葉片的長度L為半徑，作角速度為ω的勻速圓周運動，天線波束指向與旋翼葉片切線方向垂直。

下面考慮直升機運動的情況，假定在成像過程中，直升機平臺在z=H平面上沿x軸以速度vx向前運動，如圖1(b)所示。令ta為方位時間變量，定義ta=0時刻，天線相位中心位于(L,0,H)。ta=tp時刻，波束中心照射在坐標為(rpcosθp,rpsinθp,0)的點目標P上，其中rp和θp分別是點目標P在XOY平面中對應的半徑和與x軸夾角。則ta時刻雷達天線相位中心的位置(xAPC(ta),yAPC(ta),zAPC(ta))可表示為

(1)

式中，θ=ωta是ta時刻旋翼與x軸的夾角。

(a) 直升機懸停情況

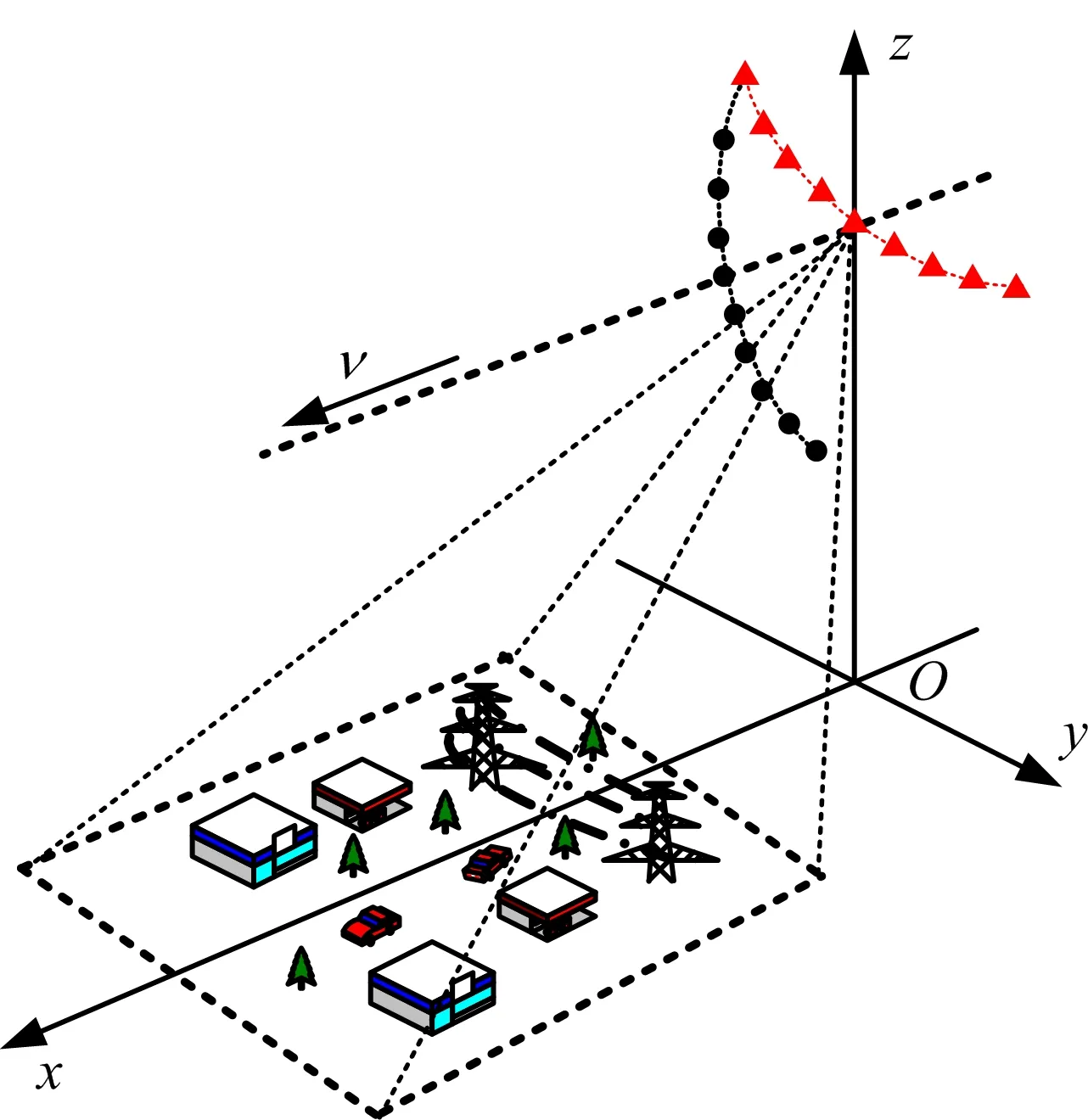
(b) 直升機前行運動情況圖1 直升機ROSAR成像幾何模型

因此，ta時刻點目標P相對雷達天線相位中心的瞬時斜距可表示為

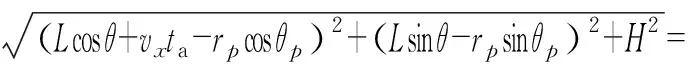
(2)

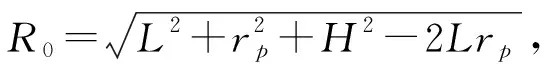
R(ta)≈

(3)

式中，

(4)

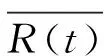
2 直升機平臺運動引入的斜距誤差影響分析

假設在成像時間內，直升機在z=H的平面上沿x軸勻速向前運動，圖2給出了z=H平面上，天線相位中心理想運動軌跡(平臺靜止)和真實運動軌跡(平臺運動)對比，主要仿真參數為：直升機飛行高度為2 000 m，直升機前進速度為50 m/s，螺旋槳旋轉角速度為40 rad/s，天線下視角為45°，旋翼葉片的長度為2 m。可以看出，直升機的前向運動導致真實的運動軌跡不是理想的圓弧形，而是呈現螺旋形。因此，在聚焦成像前須補償直升機運動帶來的斜距變化影響，下面從運動補償的角度分析直升機平臺前向運動帶來的斜距誤差。

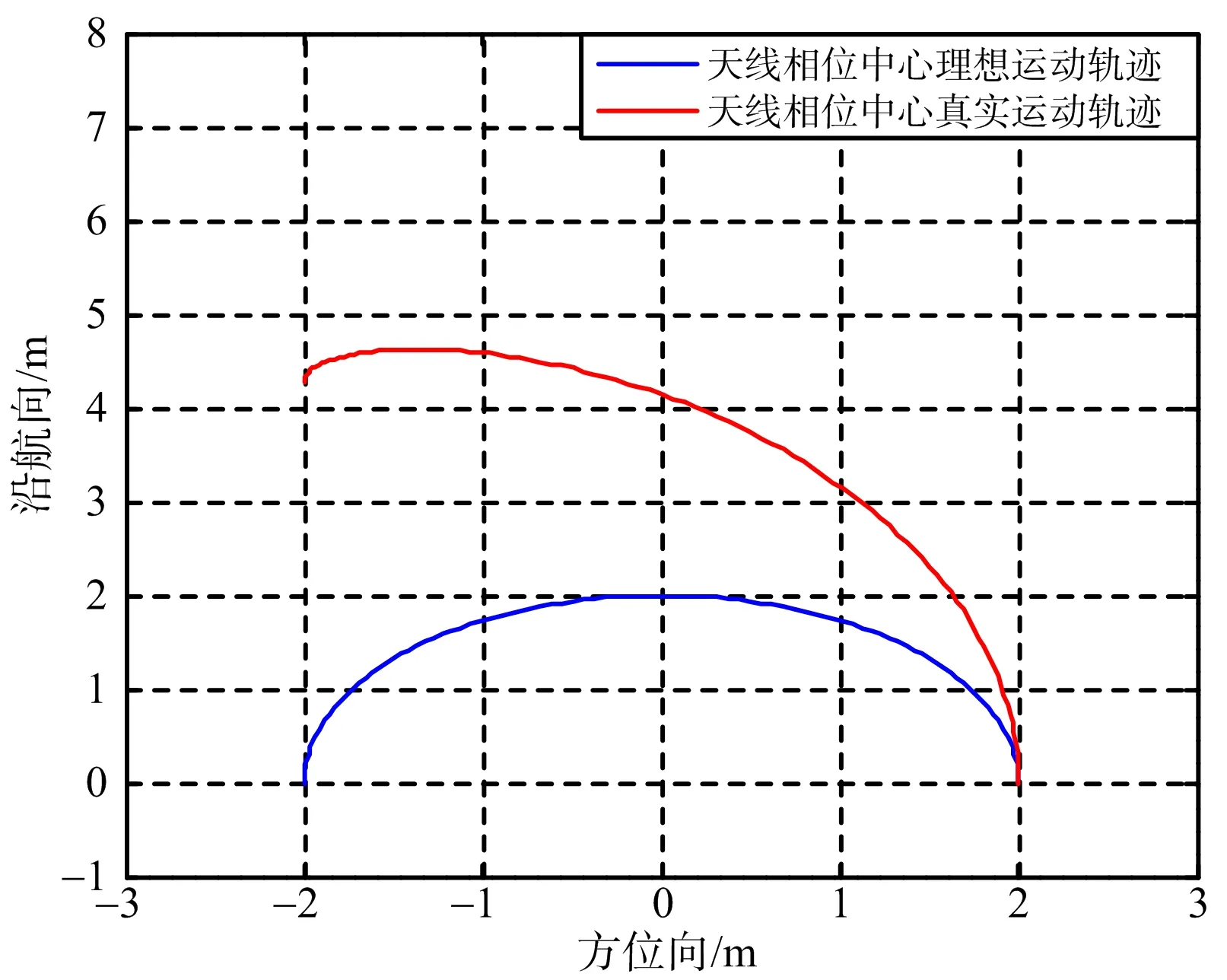
圖2 直升機平臺運動和靜止條件下的天線相位中心軌跡

由式(4)可知，直升機前向運動帶來的斜距誤差為

(5)

從上式可以看出，該斜距誤差與目標在場景中距離和方位位置相關，即該斜距誤差具有二維空變性。對場景中任意一個點目標而言，在合成孔徑時間邊緣時刻ta=Ta/2，斜距變化引起的距離單元徙動和二次相位誤差達到最大[6-7]，即

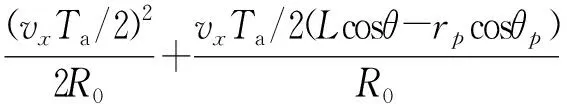
(6)

設定成像場景大小為300 m×40°(距離×方位)范圍，圖3(a)和圖3(b)分別給出了在該范圍內最大斜距誤差隨目標距離和方位位置的變化曲線。可以看出，該斜距分量的空變性非常小，因此，在補償直升機前進運動帶來的誤差時，可以直接用場景中心對應的校正函數來補償，而不影響最終的成像質量，從而極大簡化補償算法的復雜性[8]。以此為基礎，下節給出存在直升機運動情況下的ROSAR成像處理算法。

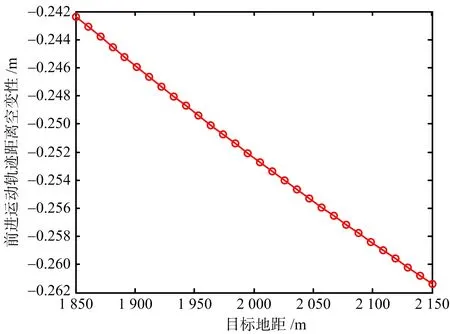
(a) 距離空變性

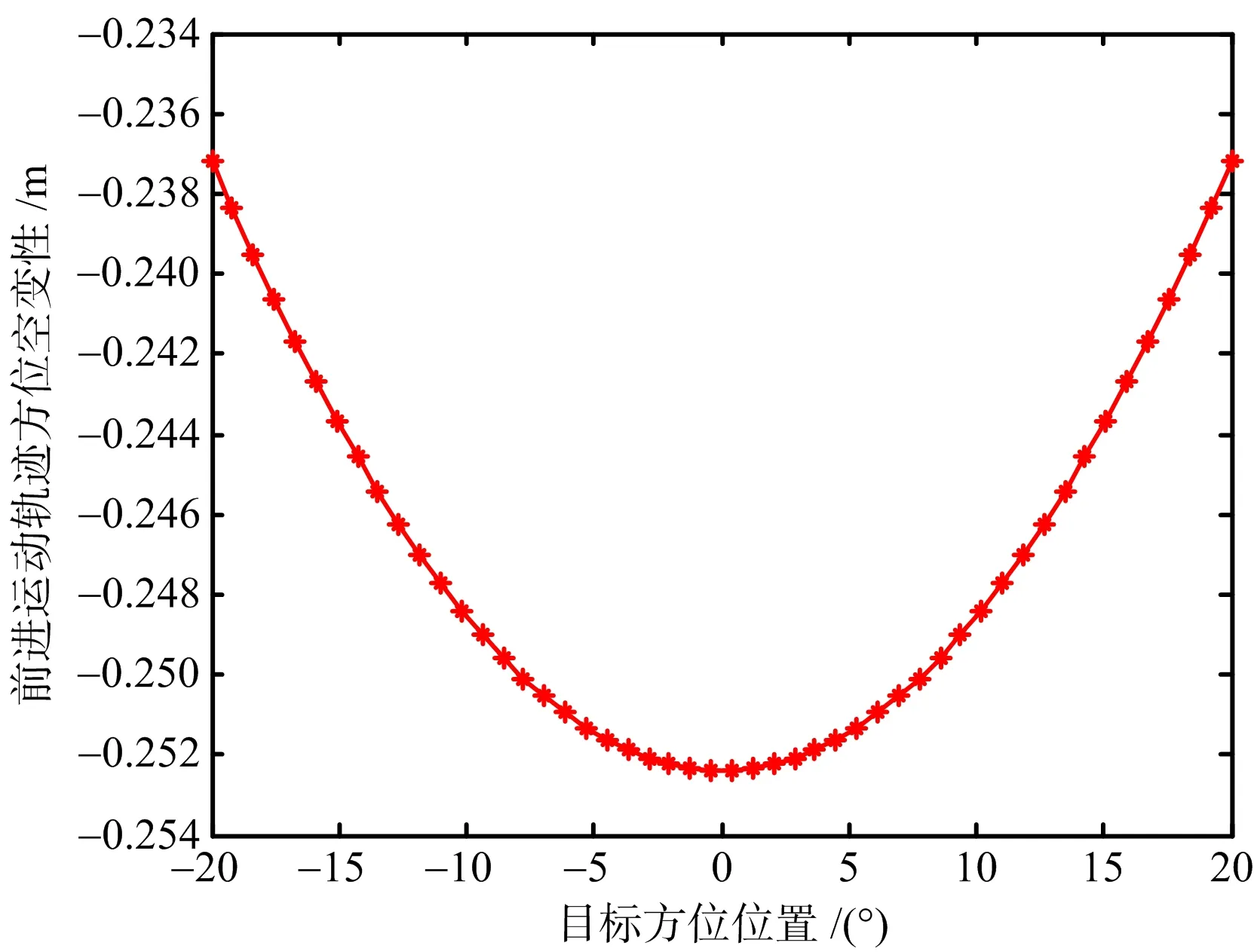
(b) 方位空變性圖3 直升機運動引入的斜距誤差空變性分析

3 直升機載ROSAR成像處理方法

本節首先對直升機載ROSAR幾何構型所特有的雷達相位中心等效速度隨目標斜距變化特性進行了分析，在此基礎上，結合運動補償思想給出了直升機平臺運動補償方法，提出一種適合于直升機平臺運動的Chirp Scaling算法。

3.1 雷達相位中心等效速度的距離空變性分析

從式(3)可知，直升機平臺靜止時的理想斜距表達式為

(7)

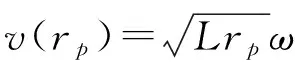
假設δθ和δrp分別是相對場景中心位置(θref,rref)的方位和距離偏移量，則該點目標處的斜距和等效速度可寫為R(θref+δθ,rref+δrp)和v(θref+δθ,rref+δrp)。在點目標處，速度近似引起的剩余距離單元徙動為

ΔRrcm(δθ,δrp)=|ΔRlrcm(δθ,δrp)|+

|ΔRqrcm(δθ,δrp)|

(8)

式中：ΔRlrcm(δθ,δrp)表示速度近似引起的線性距離徙動量，在直升機載ROSAR信號模型中，由于不存在斜視，ΔRlrcm(δθ,δrp)=0；ΔRqrcm(δθ,δrp)表示剩余二次距離徙動量，在合成孔徑時間Ta邊緣處的最大，可表示為

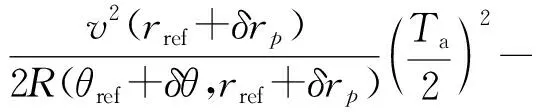
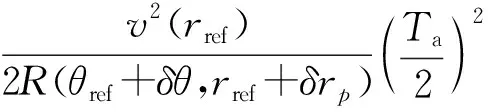
(9)

在一定成像區域內，為得到聚集良好的SAR圖像，剩余距離單元徙動須滿足如下約束：

ΔRrcm(θref,δrpmaxRCM)<γrcmρr

(10)

式中，ρr為距離分辨率，γrcm為常數，一般取1/2，δrpmax為滿足式(10)約束的偏離場景中心的最大距離。

同時，二次相位誤差須滿足如下約束：

(11)

式中，γqpe為常數，一般取1/4，δrpmaxQPE為滿足式(11)二次相位誤差約束的偏離場景中心的最大距離。

圖4(a)和圖4(b)分別給出了速度近似引入的剩余距離徙動和二次相位誤差隨目標地距變化曲線，仿真參數如表1所示。由圖4(a)可以看出，速度近似誤差引起的剩余距離單元徙動遠小于距離分辨率，因此忽略該誤差不會影響成像質量[6]。而由圖4(b)可以看出，在距離向范圍為400 m的成像場景中，大部分區域的二次相位誤差超過π/4。因此，在成像過程中，必須補償速度空變性引起的二次相位誤差。

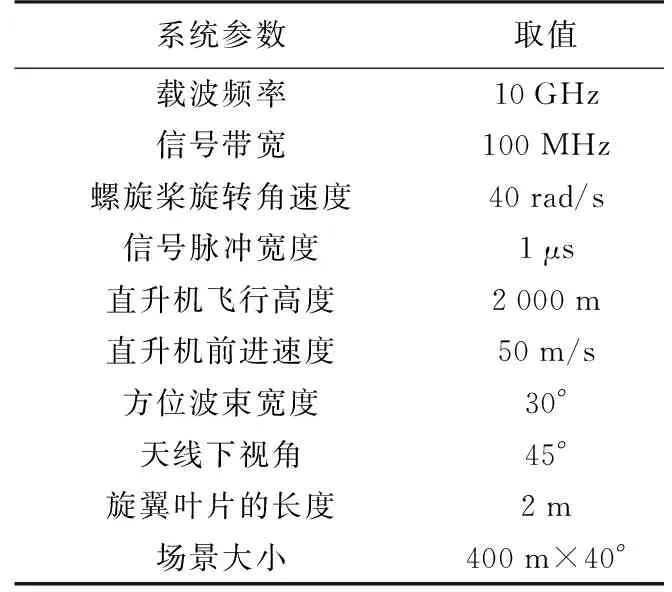
表1 直升機ROSAR系統仿真參數

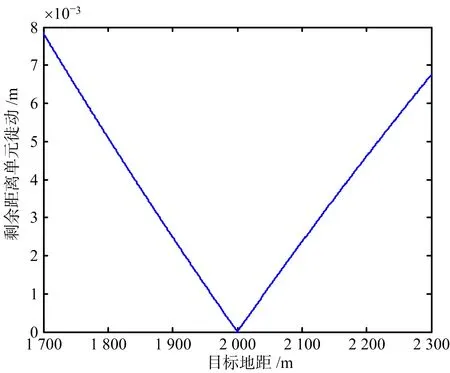
(a) 剩余距離單元徙動隨目標地距變化曲線

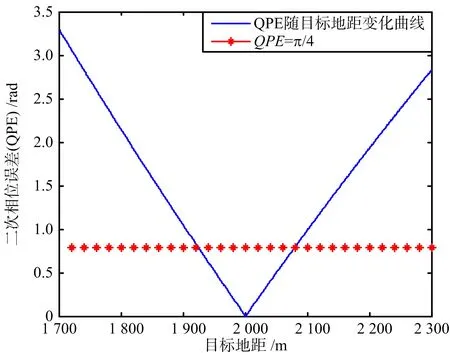
(b) 二次相位誤差隨目標地距變化曲線圖4 速度近似引入的誤差分析

3.2 改進的Chirp Scaling算法

雷達發射線性調頻信號，去載波后的點目標回波信號[6-7]可以表示為

ss(tr,ta)=

(12)

式中，tr表示快時間，c表示光速，λ表示波長，Kr表示調頻率，wr(·)和wa(·)分別表示距離窗和方位窗函數。沿快時間進行傅里葉變換，并代入式(3)的斜距表達式，信號的距離頻域表達式為

Ss(fr,ta)=

(13)

由第2節分析可知，直升機平臺運動引起的斜距誤差的二維空變性很小，可以直接用場景中心目標位置對應的誤差統一補償，其補償函數可寫為

(14)

對補償后的回波信號進行距離向逆傅里葉變換可得

ss1(tr,ta)=

(15)

對上述信號作方位向傅里葉變換至距離-多普勒域完成距離徙動校正，并利用駐定相位原理計算其傅里葉積分，可以得到信號的距離-多普勒域[8]表示式為

sS(tr,fa)=

exp(-j2πfatp)×

(16)

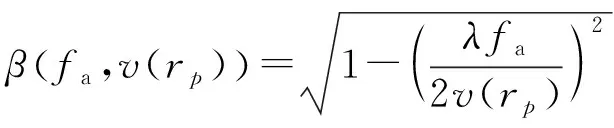
可以看出，距離單元徙動量不僅依賴于方位頻率，還與雷達相位中心等效速度有關。由3.1節分析可知，雷達相位中心等效速度隨斜距變化引起的距離單元徙動很小，因此，在距離徙動校正時可以忽略其空變性，直接用場景中心目標對應的速度來統一處理，距離-多普勒域的變標函數可寫為

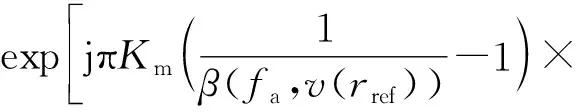
(17)

式中，rref為場景中心的地距，Rref為參考斜距，定義為雷達天線到場景中心目標的最短斜距。將式(16)和式(17)的乘積進行距離向傅里葉變換，并根據駐定相位原理計算其傅里葉積分，得到距離徙動校正后的二維頻率域[9]表達式為

SS(fr,fa)=σwr(fr)wa(fa)×

(18)

式中：第一個相位項是方位調制項；第二個相位項和第三個相位項是目標方位和距離位置的線性相位；第四個相位項是不隨目標距離變化的一致距離單元徙動項；第五個相位項是變標后的距離調制項，可以統一用參考斜距處近似補償；第六個相位項是變標處理引入的附加相位，它是距離和方位的函數，可以在方位處理時補償[10]。接著在二維頻域進行一致距離徙動校正、距離壓縮以及二次距離壓縮，完成距離向處理，再作距離向逆傅里葉變換，得到距離-多普勒信號為

sS(tr,fa)=

(19)

相應的方位壓縮函數可表示為

HAC(tr,fa)=

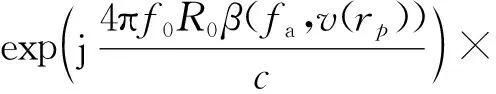
(20)

由3.1節分析可知，在方位壓縮時，必須補償等效速度v(rp)隨場景中目標斜距的變化，否則會導致目標散焦，相應的變化公式如式(7)所示。完成方位壓縮后，再進行方位逆傅里葉變換，得到最終壓縮后的目標信號為

(21)

4 仿真實驗及其分析

下面通過仿真實驗驗證所提方法的有效性，仿真參數如表1所示。場景布置如圖5所示，9個點目標按方位間隔為20°、距離間隔200 m放置。

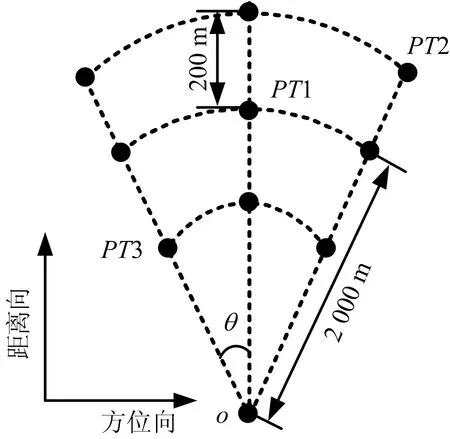
圖5 場景點目標分布示意圖

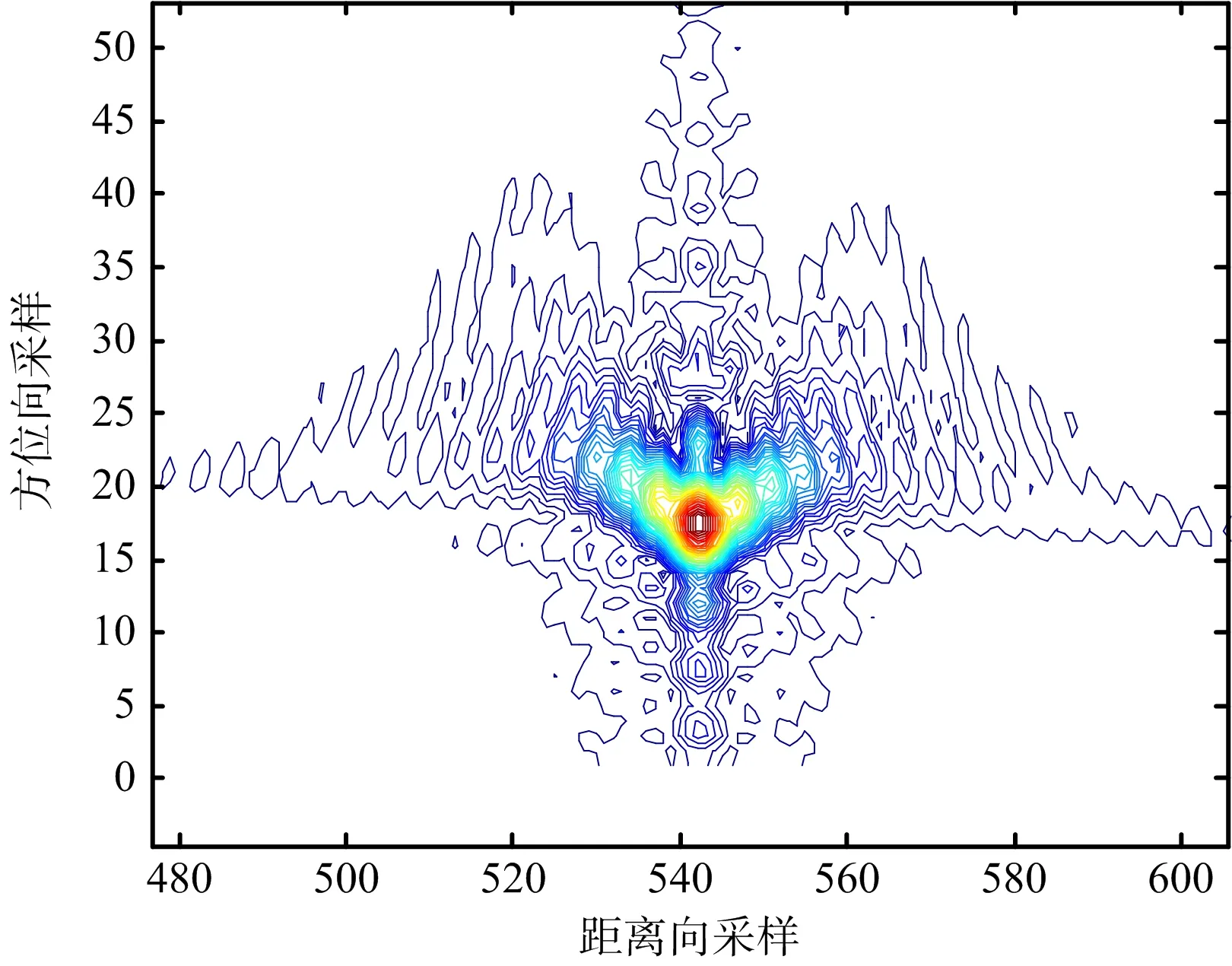
(a) 未補償直升機平臺運動的成像結果

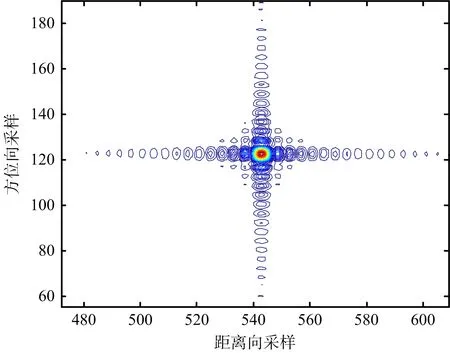
(b) 本文方法的成像結果圖6 PT1成像結果等高線圖

為了方便對比，成像時不作加窗處理。圖6～圖8給出了場景中心點目標PT1未補償直升機平臺運動的成像結果和采用所提方法的成像結果對比。其中，圖6是點目標PT1的等高線圖，圖7是距離向脈沖響應幅度圖，圖8是方位向脈沖響應幅度圖。可以看出，在未補償直升機平臺運動的情況下，點目標PT1成像結果出現拖尾和散焦，而本文方法同時考慮了直升機平臺的運動和特殊幾何構型帶來天線相位中心等效速度隨目標斜距變化的影響，得到了聚焦良好的SAR圖像，仿真結果和理論分析一致。類似地，圖9～圖11給出了場景邊緣點目標PT2成像結果對比。圖12是整個場景成像結果對比。表2依據分辨率、峰值旁瓣比和積分旁瓣比三個指標，給出了兩種方法成像質量評價結果對比。可以看出，本文提出的方法能夠得到聚焦良好的直升機載ROSAR成像結果。

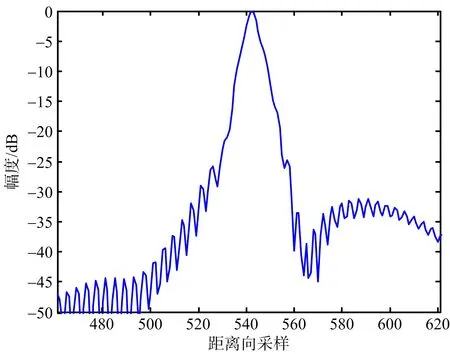
(a) 未補償直升機平臺運動的成像結果

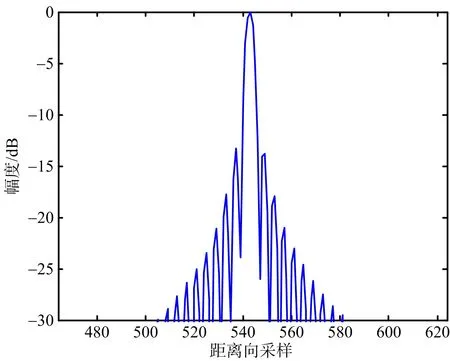
(b) 本文方法的成像結果圖7 PT1成像結果距離向剖面圖

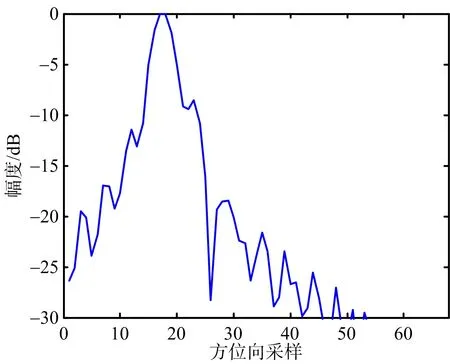
(a) 未補償直升機平臺運動的成像結果

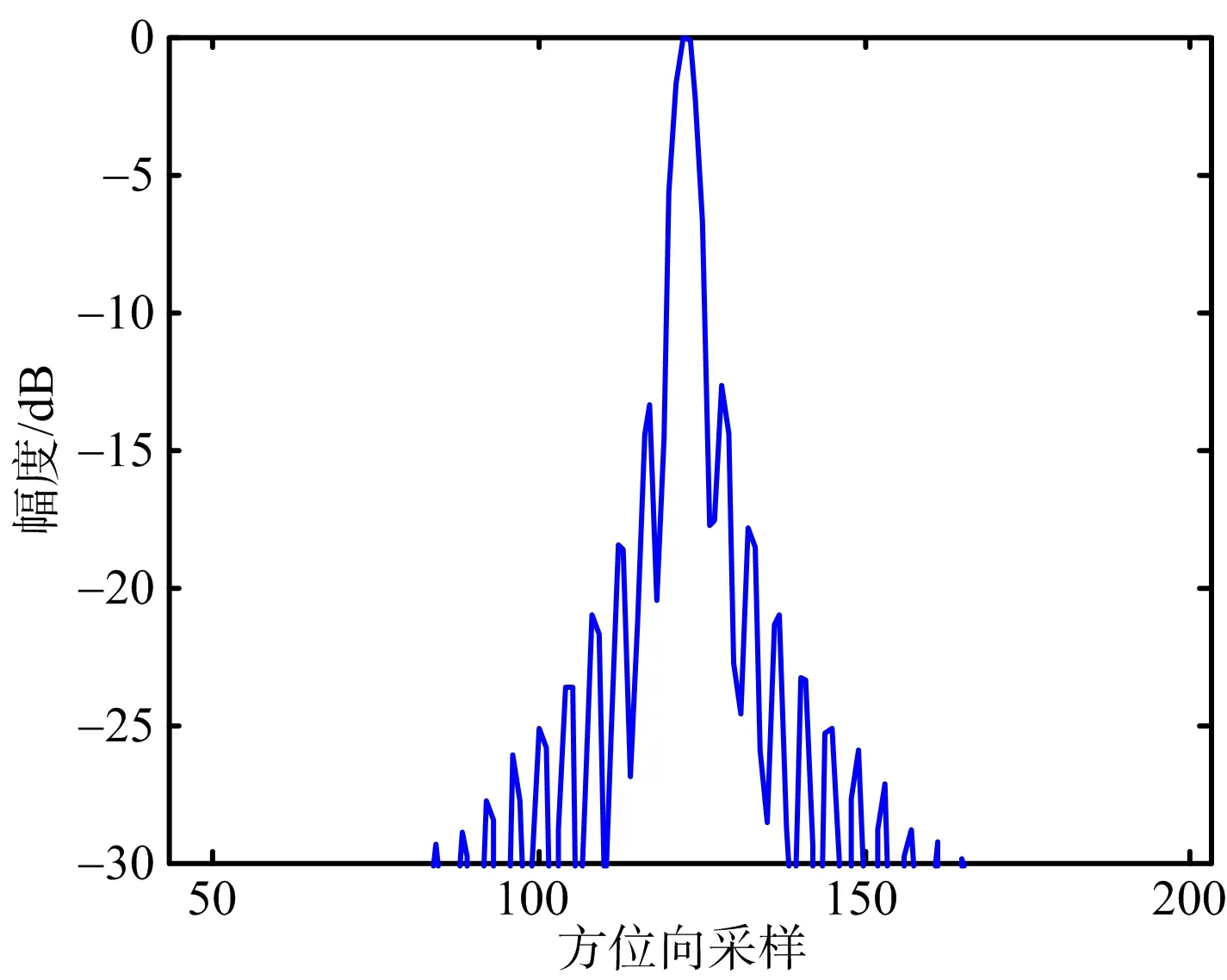
(b) 本文方法的成像結果圖8 PT1成像結果方位向剖面圖

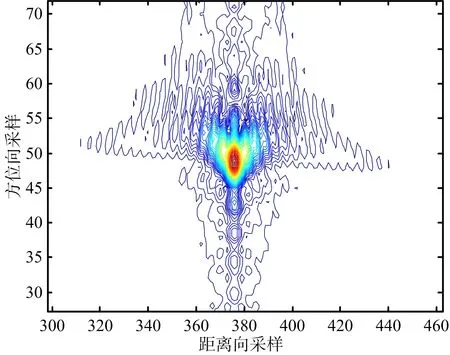
(a) 未補償直升機平臺運動的成像結果

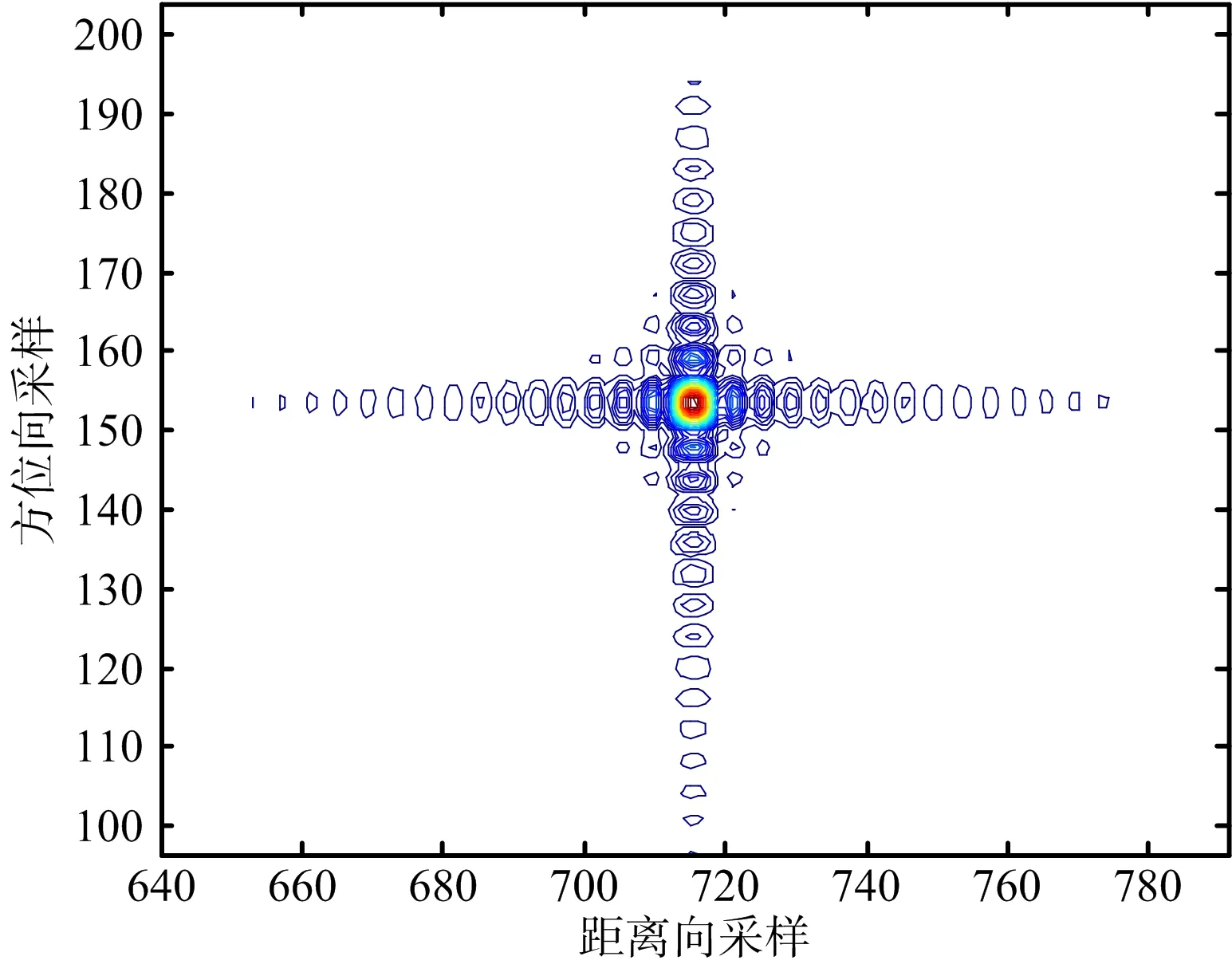
(b) 本文方法的成像結果圖9 PT2成像結果等高線圖

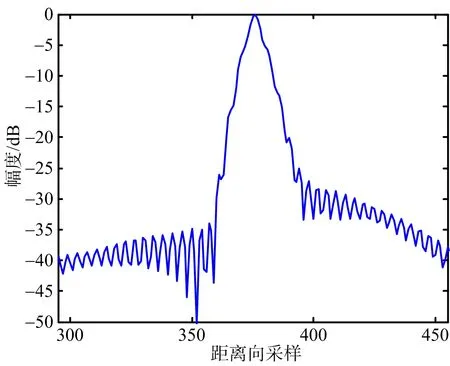
(a) 未補償直升機平臺運動的成像結果

(b) 本文方法的成像結果圖10 PT2成像結果距離向剖面圖

(a) 未補償直升機平臺運動的成像結果

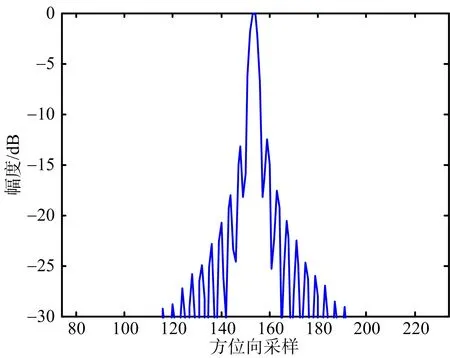
(b) 本文方法的成像結果圖11 PT2成像結果方位向剖面圖

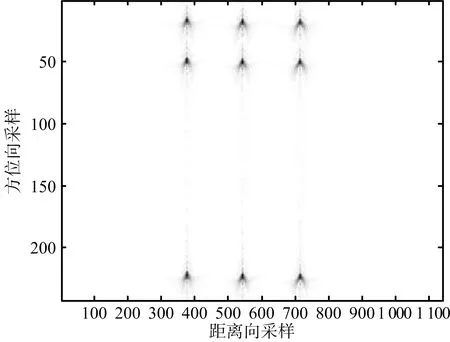
(a) 沒有直升機平臺運動補償的場景成像結果

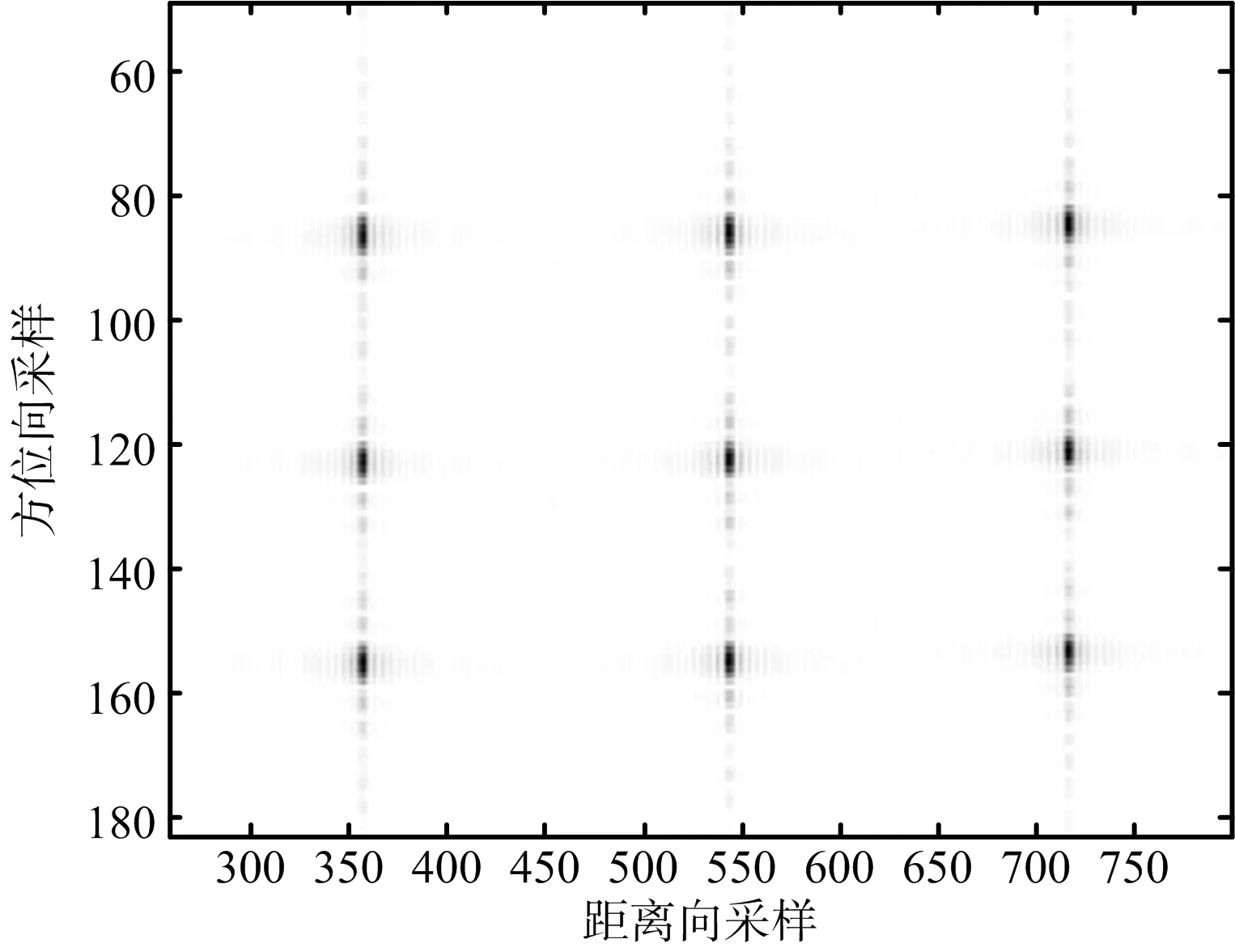
(b) 采用提出方法的場景成像結果圖12 場景成像結果對比

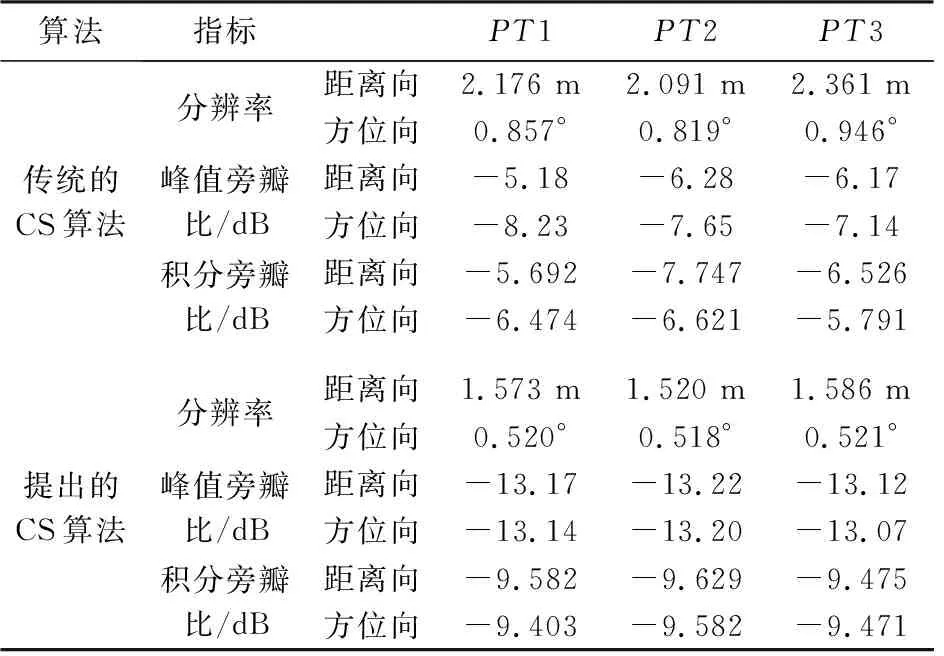
算法指標PT1PT2PT3傳統的CS算法分辨率峰值旁瓣比/dB積分旁瓣比/dB距離向2.176 m2.091 m2.361 m方位向0.857°0.819°0.946°距離向-5.18-6.28-6.17方位向-8.23-7.65-7.14距離向-5.692-7.747-6.526方位向-6.474-6.621-5.791提出的CS算法分辨率峰值旁瓣比/dB積分旁瓣比/dB距離向1.573 m1.520 m1.586 m方位向0.520°0.518°0.521°距離向-13.17-13.22-13.12方位向-13.14-13.20-13.07距離向-9.582-9.629-9.475方位向-9.403-9.582-9.471

5 結束語

本文提出一種適用于直升機平臺運動的成像算法。在分析直升機平臺運動引起的目標斜距誤差空變性的基礎上，結合運動補償思想給出了直升機平臺運動補償方法，并分析了雷達相位中心等效速度隨目標斜距變化對成像質量的影響。最后，通過仿真實驗驗證了理論分析的正確性和算法的有效性。