機載雙基雷達3D-STAP雜波抑制方法

， ， ，

(1.中國科學院電子學研究所， 北京 100190；2.微波成像技術國家重點實驗室， 北京 100190；3.中國科學院大學， 北京 100049)

0 引言

機載雙基地雷達[1]采用收發分置系統，通過將發射機和接收機分別放置在兩個獨立的平臺上，大大提高了其抗電子干擾、抗隱身技術、抗反輻射導彈、抗超低空突防(四抗)的能力，近幾年來受到了廣泛關注。但與單基雷達相比，機載雙基雷達下視工作將面臨強雜波問題。由于收發平臺的獨立運動，使雜波特性會隨著不同的雙基構型而變化，且存在嚴重的距離依賴性，給雜波抑制帶來很大困難。

空時自適應處理[2](STAP)是在時間和空間二維聯合域進行自適應處理的技術，通過在空時二維平面的雜波脊處自適應地形成凹口來抑制雜波，能獲得比一維空時級聯處理更好的性能。但是STAP需要較準確地得到目標距離單元的雜波協方差矩陣，而用于估計雜波協方差矩陣的訓練樣本需要滿足平穩且獨立同分布的條件(IID)。在單基正側視情況下，不同距離單元的雜波在空時二維平面上分布在同一條直線上，可以直接用STAP技術處理。但是機載雙基雷達系統下，雜波譜在空時二維平面上的分布會隨著距離的變化而變化，具有嚴重距離依賴性[3-4]，這會導致空時二維處理不能獲得足夠的獨立同分布樣本，使得雜波的協方差矩陣估計不準，嚴重降低了STAP的性能。

針對單基前視雷達雜波存在距離依賴性的問題，Corbell提出了一種利用陣列俯仰維信息的三維空時自適應處理(3D-STAP)技術。不同于傳統的減少樣本需求類方法[5]和雜波多普勒補償類方法[6-8]，3D-STAP方法的特點是把與距離有關的俯仰維信息[9-10]加入到雜波譜分布的描述中，使雜波譜分布由二維拓展至三維，從雜波描述的本質上消除了雜波的距離依賴性[11]。但是在雙基任意復雜結構下，3D-STAP方法是否依然適用還有待研究。本文首先驗證了存在距離依賴性的單基前視雜波在多普勒頻率-水平空間頻率-垂直空間頻率構成的三維空間中分布于同一曲面上，雜波分布特性不隨距離而改變，3D-STAP方法在此雜波分布曲面形成凹口，即可實現雜波抑制。然后在雙基任意幾何關系的前提下，發現由于雙基雷達的體制特點，使得同一距離單元處俯仰角會隨方位角發生變化，需要對3D-STAP算法作出相應改進。在引入俯仰角和方位角的依賴關系后，驗證了雙基的雜波分布特性在三維空間中不會隨距離而發生變化，即在任意距離單元，描述三維雜波分布的3個頻率之間都存在同一函數約束關系。因此，不同距離處的雜波在三維空間中分布于同一曲面，可以應用3D-STAP方法對雜波進行抑制。最后，通過仿真驗證了該方法在雙基構型下的有效性。

1 單基三維空時自適應處理介紹

圖1為機載單基雷達前視工作模式下的幾何關系圖，假設雷達平臺沿y軸方向運動，速度為v。天線陣采用前視陣列，位于xoz平面，P點為某一距離單元的一個雜波塊，其相對于天線相位中心的俯仰角為φ，方位角為θ，RS為斜距，α為視線方向與平臺運動方向的夾角，βs為視線方向和水平天線陣的空間錐角，βz為視線方向和垂直天線陣的空間錐角。

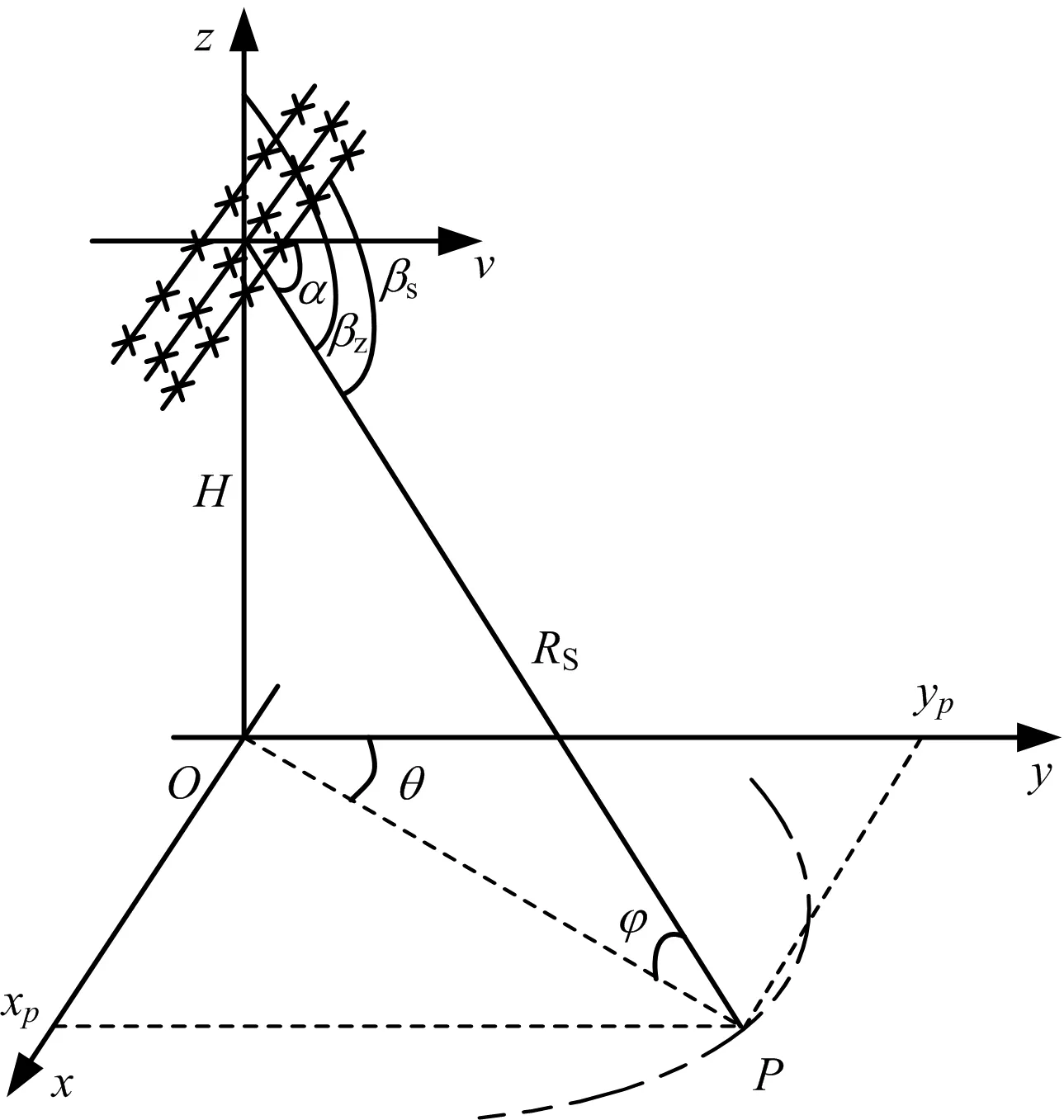
圖1 機載單基雷達幾何關系

當天線陣采取等效線陣時，為二維空時自適應處理，此時雜波中不包含俯仰維信息，只與多普勒頻率和空間頻率有關。對于地面靜止不動的散射體，其產生的雜波多普勒頻率由平臺的運動引起，為

(1)

式中，λ為發射信號波長，fr為脈沖重復頻率。

空間頻率，即回波的相位變化由天線陣元之間的間距所引起，二維STAP方法只考慮沿x方向的水平線陣。假設平臺靜止不動，以陣列中心作為參考相位中心，則位于xi處的一個陣元，其從一個地面靜止散射體接收到的信號相對于相位中心的相位差為

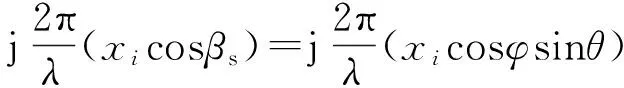
i=1,…,M

(2)

式中，M為水平天線陣列單元數。

于是空間頻率為

(3)

通常取天線陣元間距dx=λ/2。

將多普勒頻率和空間頻率分別歸一化，定義歸一化多普勒頻率為

fd=cosφcosθ

(4)

歸一化空間頻率為

fs=cosφsinθ

(5)

于是雜波的多普勒頻率與空間頻率滿足如下關系：

(6)

可以看到在二維情況下，雜波的歸一化多普勒頻率fd與歸一化空間頻率fs的關系會隨著俯仰角度φ變化，在平面上不同距離單元處的雜波分布表現為半徑不同的同心圓，如圖2所示。此時稱雜波具有距離依賴性，不同距離的雜波分布不同，尤其是近距時不同距離單元的雜波分布相差很大，給雜波抑制帶來困難。

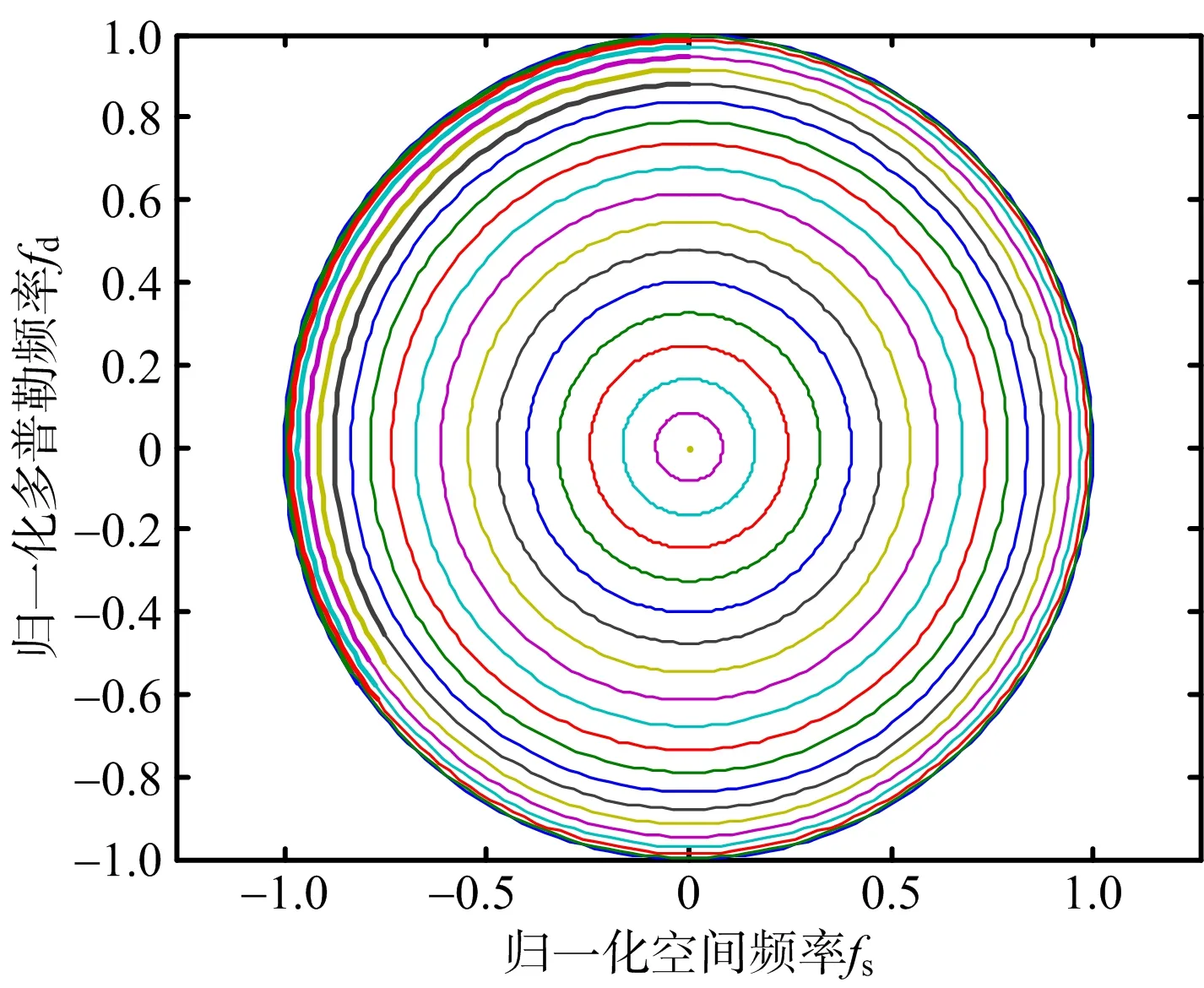
圖2 單基二維前視雜波分布

3D-STAP以二維面陣為基礎建立雜波模型。在對三維雜波分布的描述中，空間頻率被分為水平空間頻率和垂直空間頻率，二維雜波分布中距離依賴性由不同距離處的俯仰角度不同而引起，3D-STAP將引起距離依賴性的俯仰角φ加入到了雜波描述之中，變成第三維信息。利用加入的垂直空間頻率，從雜波描述的本質上消除了雜波的距離依賴性。

在加入垂直方向上的陣列單元后，對位于(xi,zi)處的一個陣元，其接收到的信號相對于天線陣相位中心的相位差為

i=1,…,M，j=1,…,N

(7)

式中，M為水平陣元數，N為垂直陣元數。

此時歸一化水平空間頻率仍為fs=cosφsinθ，垂直空間頻率fz為

(8)

歸一化后fz=-sinφ。此時，多普勒頻率fd與空間頻率fs，fz之間滿足如下關系：

cos2φ+sin2φ=1

(9)

由式(9)可見，3D-STAP的雜波模型中，多普勒頻率與水平空間頻率和垂直空間頻率之間滿足確定關系，三者的平方和等于1，即不同距離單元的雜波在三維空間中分布在半徑為1的球面上，如圖3所示。這使得三維空間中雜波分布與距離無關，3D-STAP可以在fd-fs-fz三維空間中形成三維自適應權值，通過在球面上形成凹口來實現對雜波的有效抑制，從而消除雜波距離依賴性的影響。

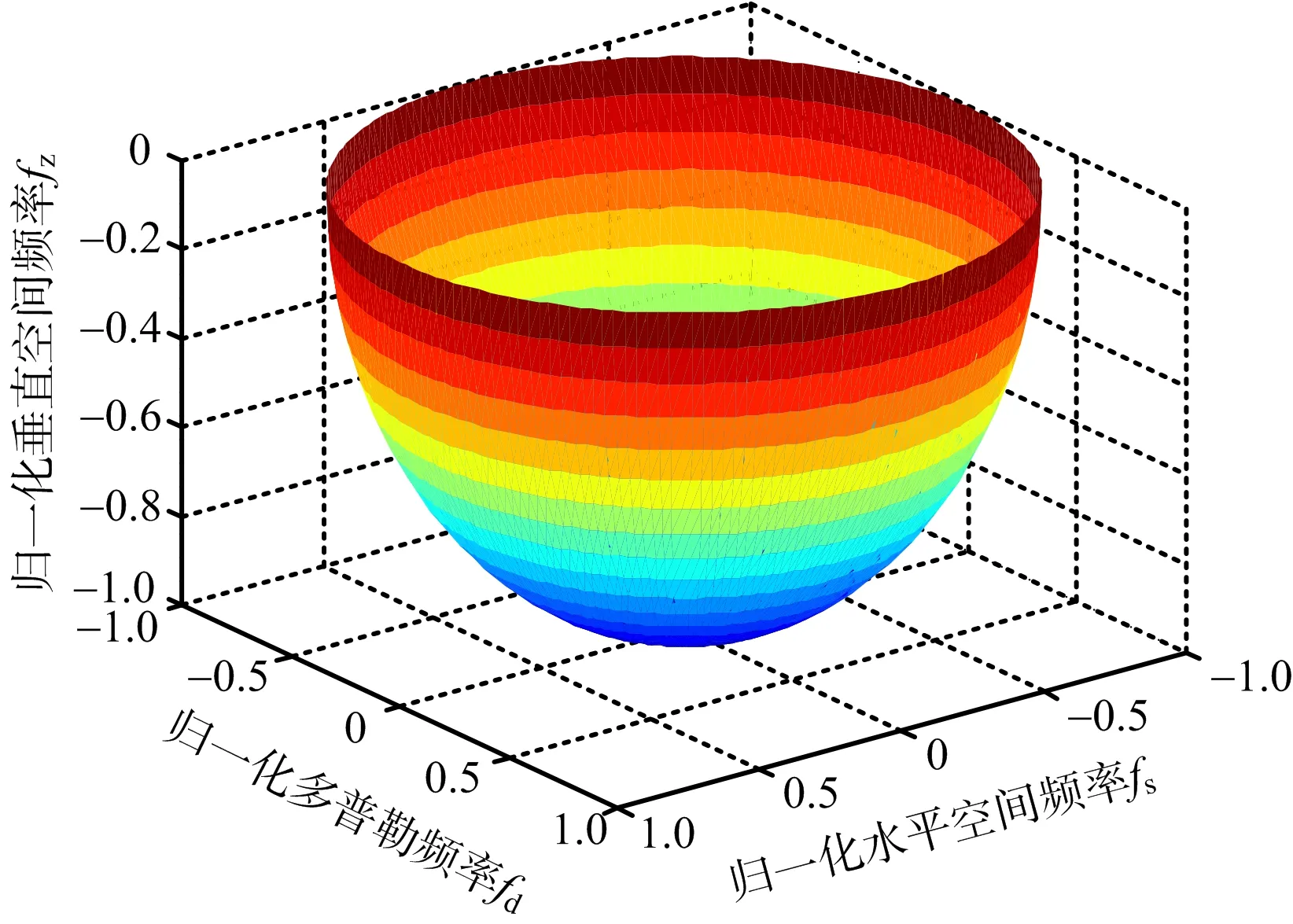
圖3 單基三維前視雜波分布

2 雙基三維空時自適應處理

2.1 雙基3D-STAP機理分析

與機載單基雷達雜波分布相比，機載雙基雷達由于接收機和發射機分置，彼此之間獨立運動，會產生多種可能的幾何場景，這使得雙基雜波分布非常復雜，雜波特性會隨著幾何場景的不同而發生變化。此時無論是正側視還是非正側視情況，雜波分布均存在嚴重的距離依賴性。

要想將3D-STAP方法應用在機載雙基情況，首先需要考慮雙基體制帶來的特殊問題。在單基情況下，等距離環均為以雷達為中心的圓環，一個距離單元處的俯仰角始終不變，但在雙基情況下，發射機和接收機的分離使得等距離環表現為不規則橢圓，這意味著在一個距離單元處的俯仰角不再是固定不變的，而會隨方位角的變化而變化。推導俯仰維信息時需要考慮其與方位向的依賴關系，接著再證明加入俯仰維信息之后，雙基雜波在三維空間中的分布不會隨距離而變化。

將接收機在地面的投影作為原點，雙基基線L在地面的投影作為y軸建立直角坐標系，任意幾何關系下的機載雙基雷達示意圖如圖4所示。

圖4 機載雙基地雷達幾何關系

圖中,HT和HR分別為發射機和接收機的高度，VT和VR為發射機和接收機的速度，接收機天線采用二維面陣，P點為某一距離單元的一個雜波塊，βT和βR分別為發射機和接收機的視線方向與水平天線陣方向的夾角，αT和αR分別為發射機和接收機的視線方向與載機運動方向的夾角,θAR為接收機運動方向與天線陣方向的夾角，前視模式時θAR=90°，θVT和θVR分別為發射機和接收機相對于y軸的運動方向，φT和φR分別為發射機和接收機的俯仰角度。

由此可寫出多普勒頻率fd、水平空間頻率fs和垂直空間頻率fz三者的表達式如下：

(10)

(11)

(12)

從圖4可以推出如下關系：

(13)

(14)

(15)

(16)

(17)

(18)

(19)

由式(12)和式(13)可得

(20)

即fz與RR存在函數關系，記作RR=F(fz)，代入式(15)，同理可得Rr=F(fz)。

考慮空間角之間的關系有cosβR=cos(θR-θVR-θAR)cosφR，代入式(11)，可得

(21)

由于θVR和θAR為常數，RR和Rr為fz的函數，所以可得fs為fz和θR的函數，即θR也為fs和fz的函數，記作θR=F(fs,fz)。

同樣由空間角關系fd可推導如下：

(22)

可見結果表達式中除去常數外，fd只與θFR，RR和Rr有關，而θFR，RR和Rr均為fs和fz的函數，所以可得fd=F(fs,fz)，即3個頻率之間存在特定的函數關系，表明不同距離單元雜波在三維空間中處于同一曲面，為抑制提供可能。當發射機和接收機均沿x軸運動，接收機采用前視模式時雜波的二維和三維分布如圖5所示。

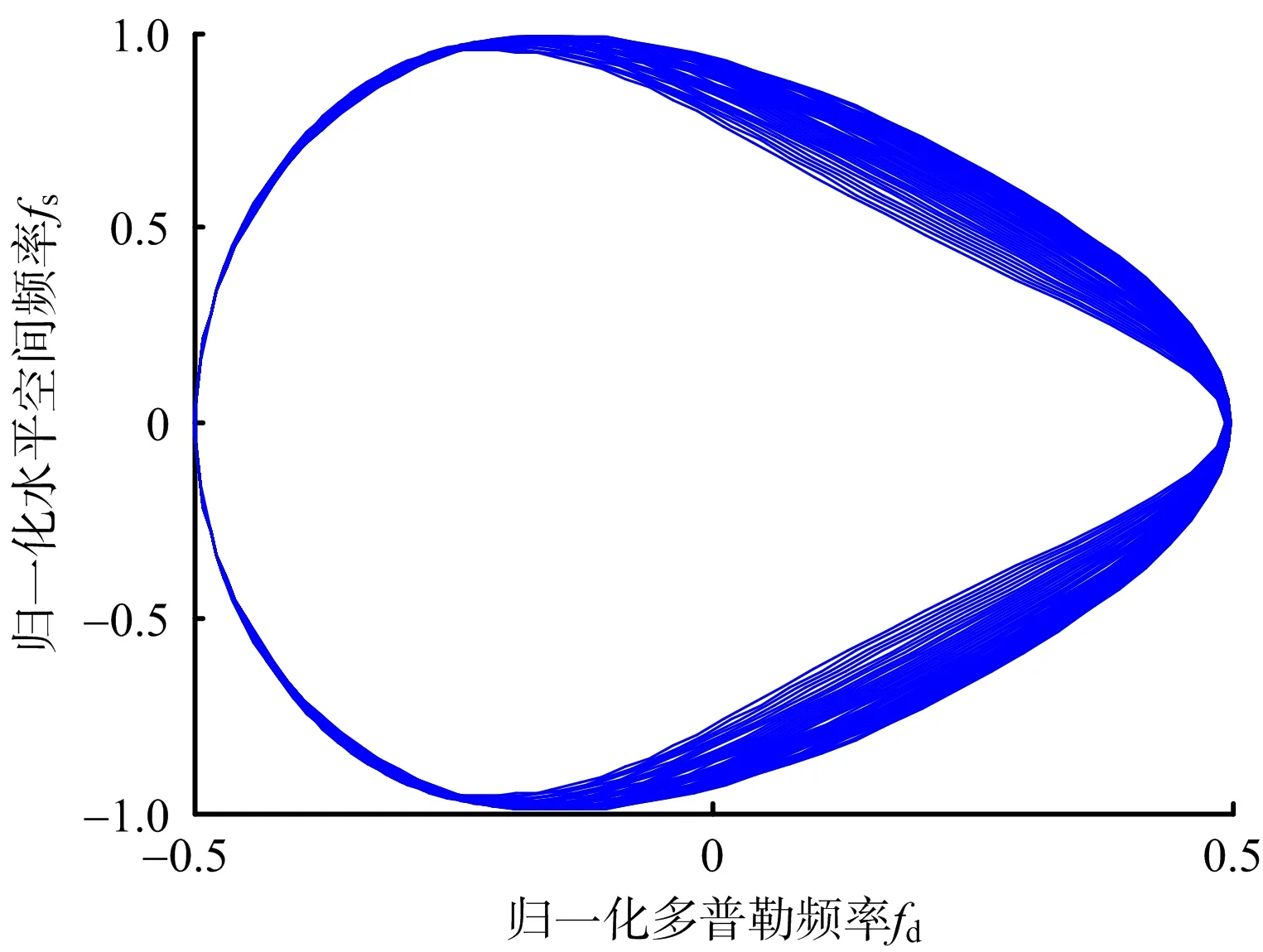
(a) 二維雜波分布

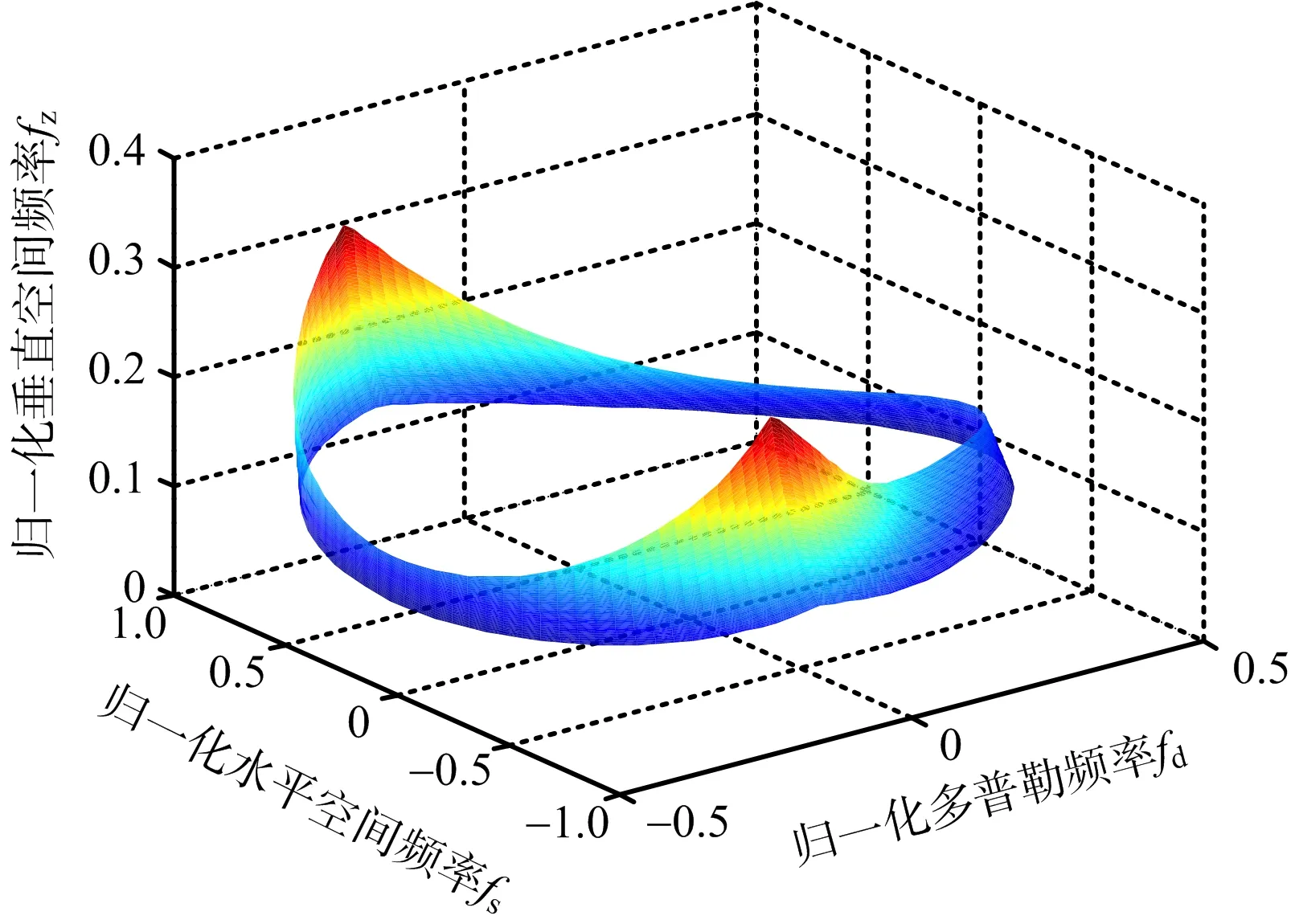
(b) 三維雜波分布圖5 機載雙基雜波分布對比

由圖5(a)可見，二維時不同距離處的雜波分布不能完全重合，具有距離依賴性，而圖5(b)中雜波雖然有距離依賴性，但在三維空間中所有的雜波譜線均分布在一個近似圓環的曲面上，可以在三維空間中對曲面進行抑制。其他幾何構型下的雜波分布情況與之類似。

2.2 雙基3D-STAP算法

3D-STAP算法的處理流程與二維基本一致，不同之處在于三維方法的空域是對M×N個陣元組成的面陣采樣，空時導向矢量中加入了垂直方向的導向矢量。當垂直方向的通道數等效為1時，可退化為二維STAP處理。假設時域對K個脈沖采樣，則三維空時采樣矢量X可表示為

(23)

式中，

Xk=[x11kx21k…xM1kx12kx22k…xM2k…

x1Nk…x2Nk…xMNk]T

(24)

式中，xmnk表示第m行n列的陣元在第k次脈沖接收到的數據，所以矢量X為MNK維。在一個相干處理間隔內不同距離單元的三維采樣數據的俯仰信息可以認為近似相同，所以雜波的三維空時協方差矩陣可以由如下統計方法計算：

RX=E[XXH]

(25)

協方差矩陣RX為MNK×MNK維，實際中RX一般由與待檢測距離門相鄰的若干距離門的數據估計得到，假設待檢測距離門的數據為X，與其相鄰的L個距離門的空時快拍數據則為X(l),l=1,2,…,L，因此協方差矩陣RX的估計式為

(26)

與二維空時處理相同，三維空時自適應處理的權矢量W同樣由以下約束得到：

(27)

其最優解為

(28)

式中，S為三維空時導向矢量。

S=SS(ωx,ωz)?ST(ωfd)

(29)

式中，“?”表示Kronecker積，SS(ωx,ωz)表示二維的空域導向矢量，ST(ωfd)表示時域導向矢量，而空域的導向矢量由水平和垂直維的導向矢量得到，即

SS(ωx,ωz)=SSX(ωx)?SSZ(ωz)

(30)

3個導向矢量分別為

SSX(fs)=[1 exp(j2πfs)…

exp[j2π(M-1)fs]]T

(31)

SSZ(fz)=[1 exp(j2πfz)…

exp[j2π(N-1)fz]]T

(32)

ST(fd)=[1 exp(j2πfd)…

exp[j2π(K-1)fd]]T

(33)

式中，多普勒頻率fd、水平空間頻率fs和垂直空間頻率fz三者的表達式見式(10)～式(12)。

3 仿真實驗

分別用2D-STAP和3D-STAP方法對機載雙基雷達典型構型下的雜波進行抑制，采用改善因子IF作為雜波抑制性能的評價指標。改善因子的定義為系統輸出信雜噪比與輸入信雜噪比的比值，用來反映自適應系統對數據信雜噪比的改善能力，可以有效表示自適應系統的性能。其表達式如下：

(34)

3.1 參數設置

實驗主要對仿真數據進行處理，實驗的參數設置如表1所示。其中二維場景中的垂直通道由4個陣元通過波束形成得到。

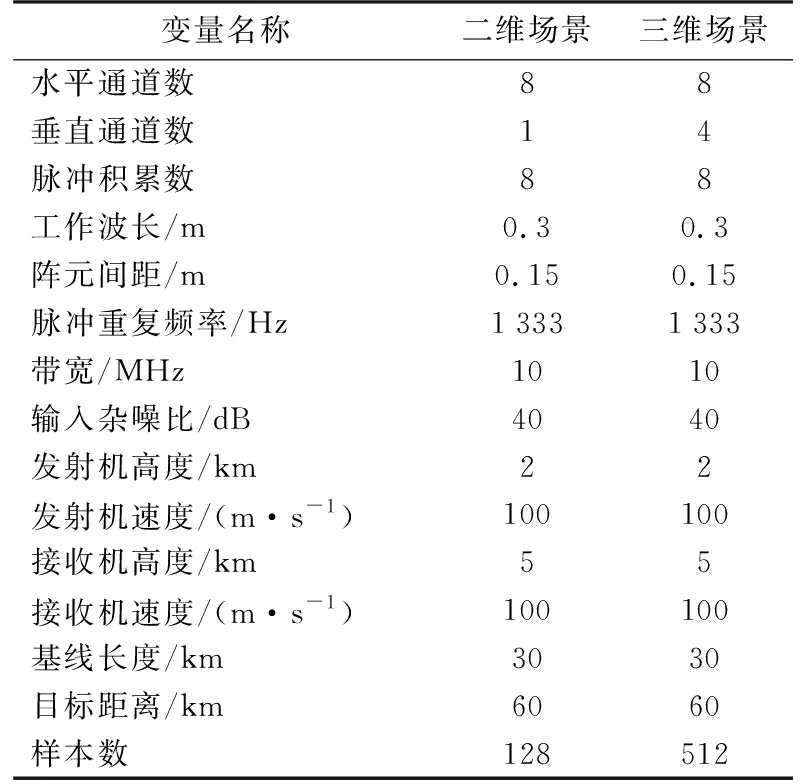
表1 仿真參數

3.2 仿真實驗1

當發射機運動角度θVT=90°，接收機運動角度θVR=0°，接收機天線為正側視時，目標距離處的雜波功率譜如圖6所示。截取接收機方位角余弦值為0.05處的歸一化改善因子進行對比，結果如圖7所示。

圖6 構型一雜波功率譜

圖7 構型一改善因子對比

對比圖7中的改善因子可以看出,3D-STAP的改善因子凹口相對更窄，在靠近凹口處3D-STAP要比2D-STAP高5 dB左右，說明三維方法在靠近主雜波區時的性能改善明顯。

3.3 仿真實驗2

圖8 構型二雜波功率譜

圖9 構型二改善因子對比

在另一種較為復雜的幾何關系下，發射機運動角度θVT=0°，接收機運動角度θVR=90°，接收機天線為前視時，雜波功率譜如圖8所示，接收機方位角余弦值為0.54處的歸一化改善因子對比結果如圖9所示。由圖中可以得到與之前相同的結果，3D-STAP在靠近主雜波區處的性能有所改善，證明了改進后的三維方法在雙基不同幾何關系下對雜波抑制的有效性。

在仿真過程中發現,雖然3D-STAP能夠取得更好的雜波抑制效果，但是3D-STAP最優處理需要估計MNK×MNK維的協方差矩陣，并對其作求逆運算，相應的計算復雜度為O(M3N3K3)，與2D-STAP的計算復雜度O(M3N3)相比，計算量大大增加，并且處理中需要的樣本數較大，實際中需要結合有效的降維方法，降低其運算量以實現實時處理。

4 結束語

針對機載雙基雷達雜波分布在傳統的二維模型下存在嚴重距離依賴性的問題，通過驗證雜波分布特性在多普勒頻率、水平空間頻率和垂直空間頻率構成的三維空間中不隨距離而發生變化，其三維分布具有共面特性，提出可以利用俯仰維角度信息，從雜波描述上消除距離對雜波分布的影響。并充分考慮了雙基特殊體制下，俯仰角和方位角的依賴關系，對傳統3D-STAP算法作出相應改進，從理論上證明了改進后的3D-STAP方法在雙基任意幾何關系下對雜波抑制的可行性。并通過仿真與2D-STAP的改善因子進行對比，說明了3D-STAP方法結合了多普勒-方位向-俯仰向信息，使得改善因子在凹口附近提高了5 dB左右，改善了對目標的檢測性能，特別是對接近主雜波區的低速目標的檢測能力。

本文從理論上分析了機載雙基雷達的特點及其雜波在三維空間中的分布特性，將3D-STAP算法擴展至雙基情況，為雙基雷達雜波抑制提供了一種更為有效的解決思路，推動了雙基雷達系統雜波抑制和動目標檢測技術的發展。