基于聲速梯度的聲納浮標工作深度選擇?

章堯卿 胡柱喜 劉 克

（1.海軍航空大學 煙臺 264001）（2.91049部隊 青島 266000）

1 引言

海洋環境對聲納作用距離的影響主要表現在聲速梯度、海區深度、海底底質和海況等方面。在等溫層或弱負梯度層環境下，聲波基本為直線傳播，聲波能量在空間分布比較均勻，此時聲納作用距離只取決于聲納系統本身和目標聲學特性［1］。但在非良好水文條件下的聲波不是直線傳播，聲波能量在空間也不是均勻分布的，這時聲納系統作用距離還與聲速梯度、聲納深度和目標深度有必然關系，其中，聲速梯度對作用距離影響最大［2］。下面主要針對不同的聲速梯度來分析聲納浮標的工作深度問題。

2 聲速梯度的影響因素

對于大多數海洋區域而言，聲速的垂直梯度約為水平梯度的1000倍。僅暖流和寒流交匯區域，水平梯度有時與垂直梯度相比擬。因此，在一級近似下，可以把海洋看作是一種平面分層介質，其聲速特性僅隨深度變化而變化，而在水平面內保持不變［3］。

聲納浮標搜潛系統包含溫度深度測量浮標，用來測量海區的溫度-深度剖面。溫深浮標的測溫探頭在入水后以一定速度下沉（約為1.5m∕s），下沉過程中實時將海水溫度發回監聽飛機［4］。溫深浮標并不是直接測量海水聲速，而是測量不同深度處海水介質的溫度，再通過相應的換算公式將溫度連同其它因素轉換為聲速。

聲波在海水中傳播的速度與海水溫度、鹽度及靜壓力有關。海水的溫度越高，鹽度和深度越大，聲速越高。鑒于影響聲速的因素復雜，難以由理論計算求得，為此經大量實測，建立了如下的經驗公式［5］：

c=1450+4.21T-0.037T2+1.14(S-35)+0.0175H

（1）式中：c為聲波傳播速度，單位m∕s；T為海水溫度，單位℃；S為海水鹽度，單位‰；H為水層深度，單位m。

通過分析上式可以看出，溫度增加1℃，聲速變化近似4m∕s；鹽度每增加1‰，聲速增加1.14m∕s；壓力增加1個大氣壓，聲速增加0.175m∕s。在影響聲速大小的溫度、鹽度和靜壓力（或深度）幾個因素中，以溫度影響最為顯著。在使用聲納浮標的有限范圍的海區內，其鹽度和壓力的影響通常是較小的，相對于溫度對聲速的影響可以忽略不計，通常在計算時將其設為常數［6］。

3 海洋聲速垂直剖面的類型

在海洋表面，由于受到海面的冷熱交換和風浪的攪拌作用，在海表以下一定深度內海水溫度基本不變，形成混合層；混合層的深度在不同的海域各不相同，對應到聲線剖面上，由于溫度不變，海水的聲速主要受壓力的影響，隨深度增大緩慢增大，形成一個聲速梯度為正梯度的聲學層，該層的最大深度稱為聲學層深度［7］。在混合層下，隨著深度的增加，海水溫度急劇降低，形成溫躍層，對應的聲線剖面上出現一個負梯度的聲速層。隨著海深的繼續增大，到一定深度，海水上下層的熱量交換基本達到平衡，溫度基本不變直至海底，形成深海等溫層。反映在聲線剖面上，受海水的靜壓力影響，聲速隨深度增大［8］。

在典型沿岸淺海及大陸架上，聲線剖面受到較多因素的影響，比深海有更大的變動性，但平均而言，仍然有比較明顯的季節特征，在冬季的典型聲線剖面是等溫層，而在夏季則為負躍層［9］。

圖1 垂直聲線剖面類型

根據理論分析，海洋中聲線剖面垂直分布類型共有如圖1所示的八種類型。但這八種類型只是理論上的抽象分類，從理論原則上進行分類指導，具有理論指導意義。實際的海洋環境中，聲線剖面可能更為復雜，所以在實際使用中要結合具體的海域水聲環境特點來確定具體的聲速類型。

圖中在中緯度的深海環境中可能出現的聲速垂直剖面類型為第III種、第VI種類型，在兩極海域會出現第I種類型的聲速垂直剖面，其它的類型基本不可能出現在深海環境中［10］。由于淺海環境的復雜多變，這八種聲速類型都有可能出現，只是聲速梯度與深海環境相比要小很多。判斷所處海域聲線剖面類型更為準確的方法是根據海區的聲線剖面歷史數據進行分析。

4 分層介質中的聲線軌跡

海洋中聲波的傳播在數學上可以用波動方程的解來描述，這個解是在特定問題的相應邊界條件和介質條件下得到的。波動方程是聲壓p對坐標x、y、z和時間t的偏微分方程，可以寫為

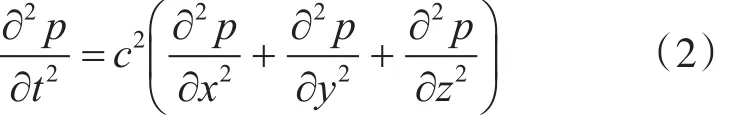
式中，c是具有聲速量綱的量，并可隨坐標變化。

有兩種理論方法解波動方程。一種是簡正波理論，另外一種解法是射線理論。射線聲學具有形象直觀的優點，它用聲線圖給出傳播的圖像。但是，在一個波長的距離內，射線的曲率半徑或聲壓振幅有較大的變化時不能給出完美的解［11］。但是，射線聲學本身有其明顯的優點，就是簡單、明了、物理意義清楚，因而在解決某些問題和分析某些現象時是必不可少的。對于高頻情況，射線理論有足夠的準確性［12］。

在確定海水中聲線軌跡的時候，我們最關心的是分層介質中的聲線軌跡。由于分層介質的聲線剖面，可以看作是很多層線性的聲速斷面的合成，所以我們首先來說明具有線性聲線剖面的情況。在這種情況下，聲速c與深度z的關系為

其中g為聲速梯度，A是一個常數，z代表深度。

聲線軌跡上兩個點的深度差Δz=z2-z1可以由式（3）求出：

應用斯涅爾（Snell）定律（見圖2）：

式中φi和φr分別表示聲線入射路徑和折射路徑與分界面的法線之間的夾角；θi和θr分別為入射聲線與折射聲線與分界面之間的夾角。ci和cr分別為入射聲線與折射聲線所在介質中的聲速。由式（4）可知，如果用c0表示聲線在水平時的聲速，那么任何深度上的聲速可以表示為

將式（4）和式（6）合并得到：

將上式積分，便得到：

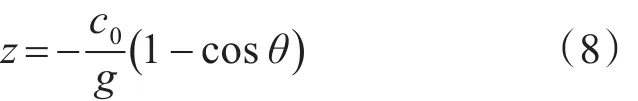
這是一個曲率半徑為-c0g的圓弧方程。

圖2 斯涅爾定律示意圖

如果聲線剖面不是線性的，那么我們可以用分層的方法進行處理，用折線去逼近任意形狀的剖面。在每一段折線所對應的那一層海水中，聲線軌跡都是圓弧，區別是圓弧的曲率不同，整條聲線就是由一段段具有不同曲率半徑的圓弧連結起來的。

當g＞0時，稱為正梯度，這時曲率半徑為負，聲線朝上彎曲；當g＜0時，稱為負梯度，這時曲率半徑為正，聲線朝下彎曲；當g=0時，曲率半徑為無窮，聲線軌跡為直線。

5 深度設定實例

根據射線聲學理論，由于聲速梯度的分布和聲納所處的深度不同，造成從聲納發出的所有聲線中只有一部分聲線將通過海水中的某一個局域范圍。當聲線足夠密時，把各聲線的聲強相加求平均，可作為這一局域范圍中心聲強的近似值。從直觀上來講，在聲線軌跡圖上聲線密度較大的地方，傳播到的聲能量較大，傳播損失較小，反之，聲線密度較小的地方，傳播到的聲能量較小，傳播損失較大［13］。通過聲納方程的分析可以知道，在其它條件不變的情況下，某一點的傳播損失越小，那么聲納就越容易發現該處的目標。所以通過聲線軌跡圖可以指導給出聲納浮標的最佳工作深度，下面就給出幾個實例。

圖3給出的是黃海某處2、4、11三個月份聲速的垂直分布圖，海深為70m。其中2月份的聲速呈現輕微的正梯度；4月份的聲線剖面屬于聲道型，但是由于聲速隨深度的變化并不明顯，基本上可以將其視為聲速均勻分布；11月份的聲線剖面為典型的負躍層情形。

圖3 黃海某處不同月份聲速垂直分布

下面就采用射線理論，通過仿真計算繪制出這三個月份的聲線圖，分別如圖4、5、6所示。三幅圖中（a）圖都是假設聲納浮標工作深度設定為15m，（b）圖都是假設聲納浮標工作深度設定為40m（由于海深只有70m，故沒有考察聲納浮標的另外一個工作深度150m）。

6 結語

通過實例仿真計算，分析可得出如下結論：

1）圖4的聲線剖面呈現輕微的正梯度，從聲線圖上可以看出，不論浮標位于15m還是40m，聲線都輕微的向海面彎曲，海面附近傳播損失較小，也就是說這兩個深度均比較適合于探測靠近海面的潛艇目標。再進一步比較兩個不同深度聲線軌跡的細微差別可以看出，如果潛艇目標位于30m以下的區域，浮標工作于40m的深度可以具有更大的探測距離。所以綜合起來就是，在輕微負梯度的情況下，應當將聲納浮標置于靠近潛艇目標可能深度的附近。

圖4 黃海某處2月份聲線剖面圖

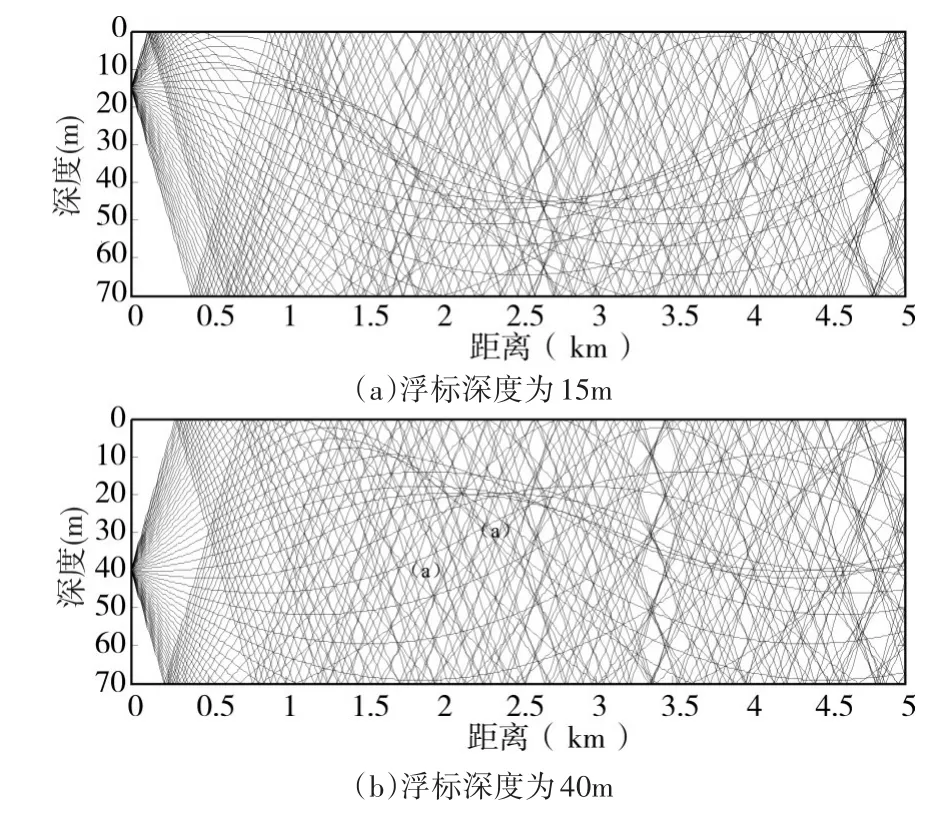
圖5 黃海某處4月份聲線剖面圖

圖6 黃海某處11月份聲線剖面圖

2）圖5的聲線剖面基本上為均勻分布，聲速從海面到海底變化不大，在傳播過程中，只有個別聲線出現了輕微的彎曲；浮標位于不同深度時，聲線圖也沒有太大的區別。所以，在接近于均勻層的海洋環境中，浮標的工作深度對探測距離基本上沒有影響。

3）圖6為典型的負躍層情形，在35m～50m左右的海深范圍內，海水具有強烈的負梯度，聲線在該范圍內也產生了明顯的彎曲。比較浮標不同的工作深度可以看出：如果潛艇目標位于躍變層以下，那么浮標在躍變層附經的工作深度上可以很容易地發現目標，而如果目標位于躍變層以上，浮標在該深度上卻很難發現目標，此時應該將浮標的工作深度也設定在躍變層以上。綜合起來，在負躍層的情況下，聲納浮標工作深度的設定要與潛艇目標的可能深度位于躍變層的同一側。即如果潛艇在50m深度以下時，浮標工作深度設定在40m更容易發現潛艇。

因此，在確定聲納浮標的工作深度時，其基本原則就是應當以實際水文條件的傳播損失為依據，根據潛艇目標可能的航行深度，尋找傳播損失最小的工作深度。