中空形行波超聲波電動機的研究

郎夢夢,曾勁松,張西平

(鄭州大學，鄭州 450001)

0 引 言

超聲波電動機是利用壓電陶瓷片的逆壓電效應和電機定子的超聲振動，借助電機定、轉子之間的摩擦耦合，從而使電機轉子運動的一種新型驅動器。超聲波電動機具有無線圈、結構簡單、設計靈活、動態響應快、質量力矩比大、高精度定位等優點[1-3]。隨著科學技術的進步，特別在空間探測、光學工程、精密儀器、汽車產業等方面，超聲波電動機的優勢逐漸凸顯[4-5]。

中空形行波超聲波電動機因中空結構的特殊性，可應用于需要中空結構的驅動平臺中，拓寬了其使用范疇[6]。中空形行波電動機可以被廣泛應用于快速執行機構、電磁兼容要求高的機構、光學和醫療器械相關的機構。現有的超聲波電動機以實心輸出軸為主，因此中空形超聲波電動機的設計極為迫切。

1 中空形電機運行機理

本文設計的超聲波電動機定子呈中空的圓環形，壓電陶瓷粘接在定子內表面，在壓電陶瓷片上施加交流電壓，通過壓電陶瓷的逆壓電效應在中空圓環上形成一個沿周向行進的面內彎曲行波。當行波在圓環上行進時，圓環外壁的質點會產生橢圓運動，從而在摩擦力的作用下推動轉子旋轉。

圓環的面內行波一般是由兩相面內彎曲振動疊加而成。要在圓環上激勵出理想的行波，必須先設法激發出圓環的2個同形、同頻、正交的面內彎振模態。

圖1 定子環模型的極坐標

圓環的2個面內彎振模態在空間上需滿足正交關系。圖1為了中空定子的極坐標簡圖。在極坐標中，定子圓環中性層的2個徑向振型函數可表示：

φ1(θ)=sin(nθ)

(1)

(2)

忽略干擾模態及結構阻尼的影響，當外界的2個振動激勵作用在圓環上時，將激發圓環產生同頻的n階面內彎振模態響應[7]：

U1(θ,t)=φ1(θ)q1(t)=K1sin(nθ)cos(αnt)

(3)

U2(θ,t)=φ2(θ)q2(t)=K2cos(nθ)cos(αnt+δ)

(4)

式中:K1,K2分別代表圓環的2個面內彎振模態的響應幅值；αn代表振動激勵的角速度，δ代表2個外界振動激勵之間的相位差。

根據線性疊加原理，定子的位移響應：

U(θ,t)=U1(θ,t)+U2(θ,t)=

(K1+K2sinδ)sin(nθ-αnt)+

2K2cos(nθ)cos(αnt)cosδ}

(5)

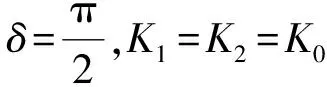
U(θ,t)=K0sin(nθ-αnt)

(6)

由振動理論可知,在定子自由狀態下,定子圓環沿圓周方向產生2階、3階以及高階振動模態。實際上由于共振頻率越高, 定子振動時內部發熱越多，所以一般優先選擇低階模態作為工作模態。振動模態示意圖如圖2所示，虛線表示變形前定子形狀，實線表示變形后的形狀。

圖2 振動模態示意圖

2 中空形電機結構設計

中空形超聲波電動機定子結構如圖3所示。根據圖3可知,此定子為中空的環形，為盡量有較大的中空空間,以及便于壓電陶瓷片的粘貼，設定定子內圈為正十六邊形。定子齒呈錐形，并呈周向分布在定子圓環上。齒與齒之間進行開槽設計，不僅可以放大周向位移，而且可以容納磨損時的磨屑。

圖3 定子結構圖

中空形超聲波電動機整體結構如圖4所示，超聲波電動機包括定子、轉子、中空底座、薄壁軸承、摩擦材料以及預壓力機構等主要構件。超聲波電動機作為一種依靠摩擦力傳遞動力的驅動器，要求定、轉子之間必須有預緊力作用，碟簧和卡簧的施加使得轉子受到均勻的軸向預壓力。定子外徑較小的一端嵌套入轉子的腔體中，環形的定子錐面與轉子相嵌，錐形的接觸界面使得轉子具有良好的自動定心作用，且可將轉子對定子的軸向預壓力轉化成周向預緊力，定子的圓周運動帶動轉子轉動，可以得到較大的驅動力矩。為了確保將定子振動的能量盡可能完全傳遞給轉子，提高能量利用率，轉子的外徑應與定子的外徑相等，因為在相同條件下，定子外徑質點的周向速度最大。支承的設計，應盡量減少對定子振動模態的影響，本文定子與中空底座通過螺紋連接，即在定子下底面的外圓周上開有細牙螺紋與底座連接，且定子與中空底座之間留出一定間隙。定子與轉子的結構便于加工，實用性強。

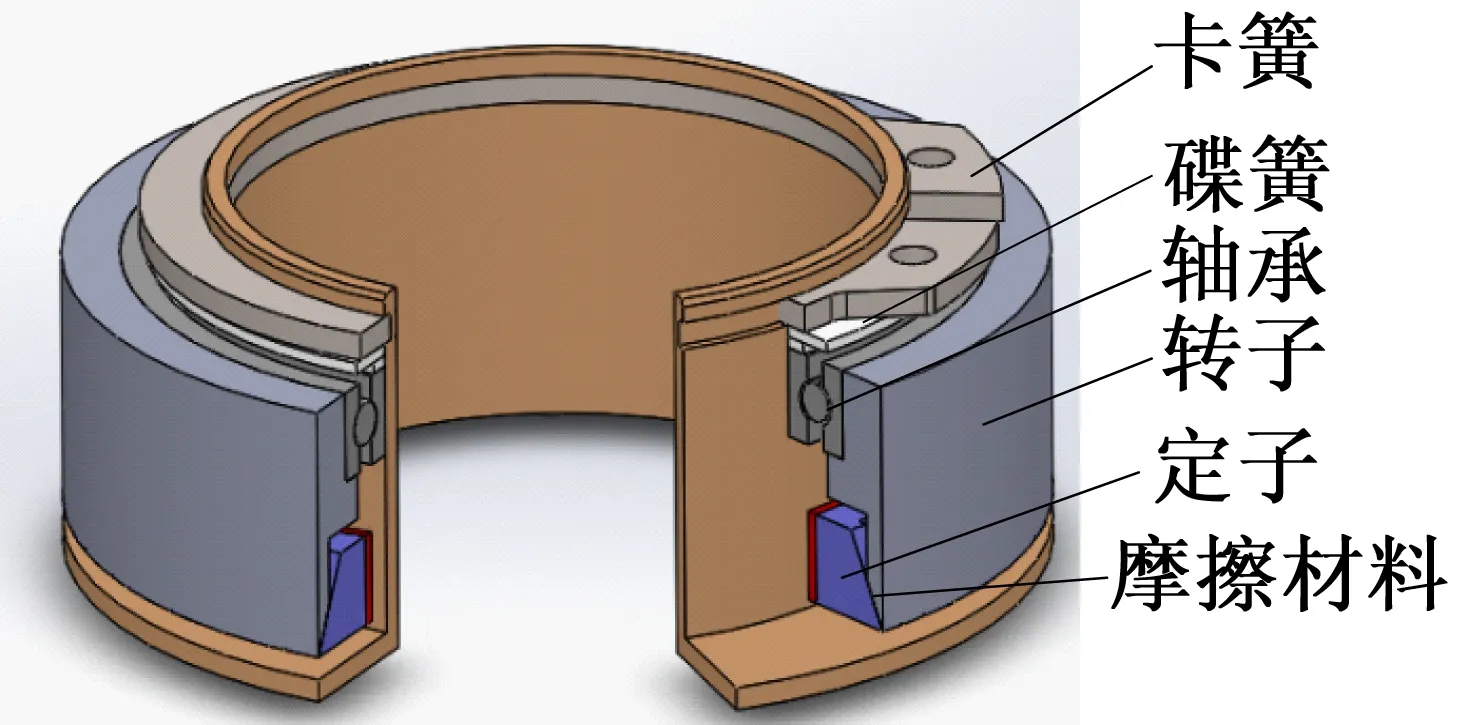
圖4 整體結構圖

3 定子模態分析

通過對中空形行波超聲波電動機進行動力學分析,能夠明確電機的機械特性[8]。模態分析可模擬超聲波電動機定子的實際振動，從而確定定子的固有振動頻率及振型。

運用ANSYS有限元分析軟件對定子及壓電陶瓷片組件進行實體建模，且定子和壓電陶瓷片的接觸采用粘接處理，并進行模態分析。本文定子的材料采用316L鋼，壓電陶瓷材料選用PZT-8。

為了滿足實際應用需求，設定環形定子下底面直徑為42 mm；為了便于轉子與定子的相嵌，錐形定子齒的斜率不宜過高，設定環形定子上底面直徑為38 mm，定子高度為4 mm。為使定子有較大的中心孔，即正十六邊形內切圓的直徑與定子下底圓的直徑比盡量接近1，設定正十六邊形的邊長為6.5 mm。考慮到加工精度，齒與齒之間的間隔寬度為1.4 mm，且齒根圓的半徑為18.5 mm,齒數為40。

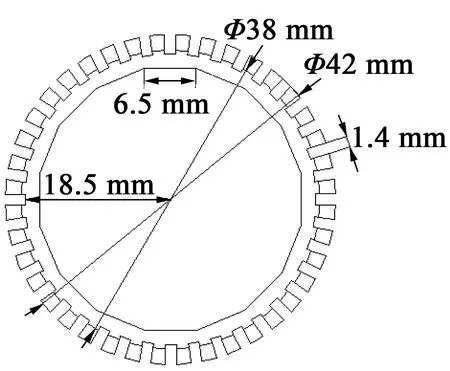
圖5 定子尺寸圖

對超聲波電動機在19～40 kHz頻率范圍進行10階模態分析，模態分析中，設置邊界條件為自由振動，忽略阻尼。分析結果如表1所示。

因高階面內振動的振動頻率相對較高，相應造成較大的振動消耗，所以本研究選用面內四階模態振型，即振動階數為1階與2階。由表1可知，面內四階振動模態頻率為21.542 kHz，與其相鄰的3階振動頻率相差5 126 Hz，相差較大，激勵時不會造成模態混疊，可以證明電機在工作時是穩定的，同時也證明了本文設計的中空式結構的電機定子的合理性。面內四階模態頻率圖如圖6、圖7所示。

表1 定子模態頻率

圖6 面內四階模態振型1

圖7 面內四階模態振型2

4 定子諧響應分析

中空形行波超聲波電動機的運轉性能與定子的振幅有很大關系，對定子進行諧響應分析，可模擬電機的實際工況，計算出定子在特定激勵電壓和頻率下的振幅。且諧響應分析可驗證模態分析所選擇的振動頻率是否為最佳工作頻率。

根據面內行波運行機理并結合實際要求設計中空超聲波電動機壓電陶瓷的粘接方式，圖8為定子施加電壓的俯視圖，16片壓電陶瓷緊貼在定子內十六邊形的孔內，壓電陶瓷的極化方向為從正號到負號，即從壓電陶瓷片的內側向外側極化。接觸定子基體一側的壓電陶瓷片接地，另一側的壓電陶瓷片電壓按照sin，cos，-sin，-cos的順序激勵出行波。

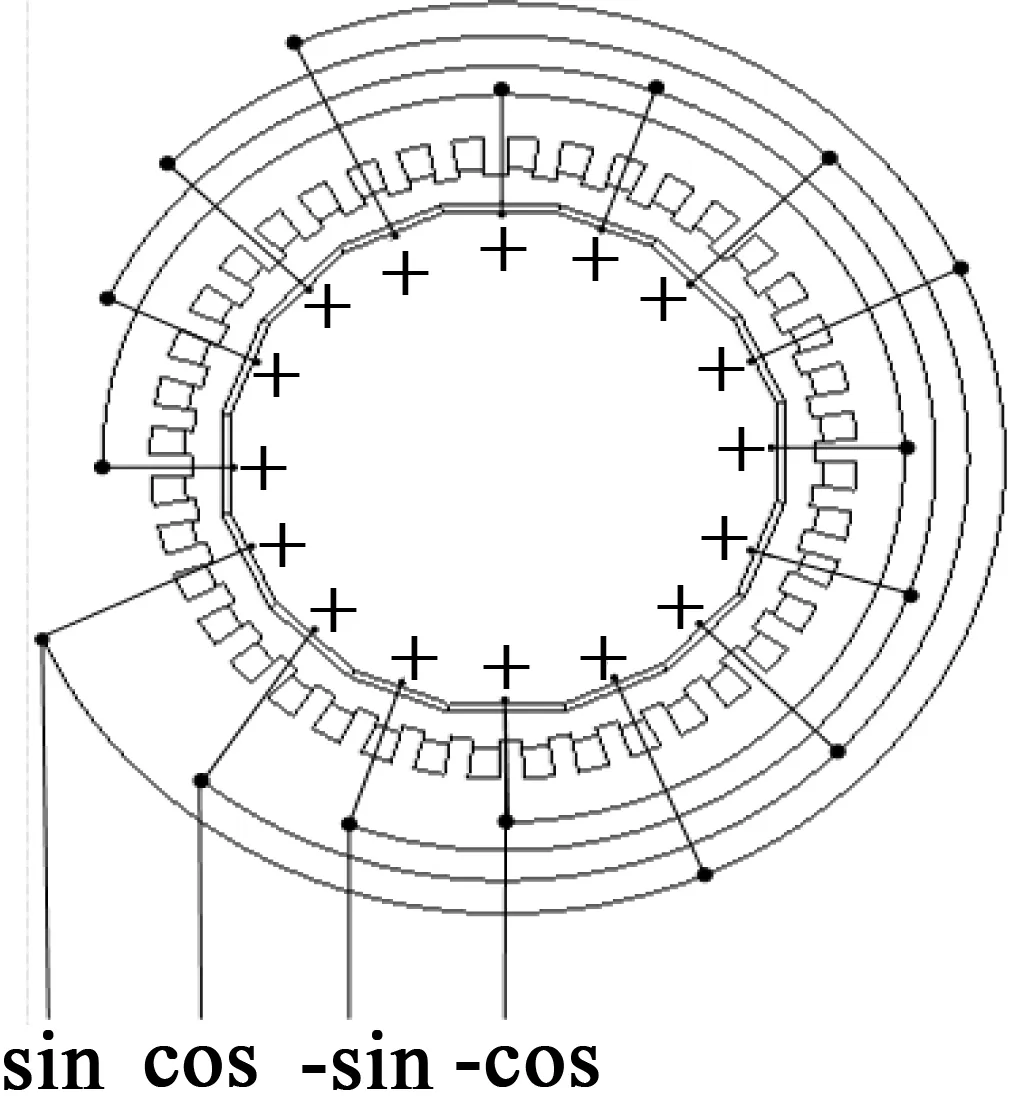
圖8 四相接線示意圖

依據工作模態頻率附近的范圍內進行諧響應分析，對此定子施加峰峰值為160V，頻率范圍為21.2～21.7 kHz的交變電壓，設定40個子步，這樣縮小了計算范圍，大大縮短計算時間。在柱坐標系中提取定子上與轉子相接觸的某一質點的徑向位移與周向位移，如圖9所示。由圖9可知，在所選頻率范圍內，質點在頻率為21.375 kHz時達到峰值，接近模態分析頻率。且徑向位移Sr為3.3 μm,周向位移Sc為2.95 μm，周向位移與徑向位移比為0.9，具有良好的輸出狀態，滿足預設要求。

圖9 質點位移圖

為提升電機的運轉性能，可通過提高電機定子表面質點周向位移和徑向位移來實現，一種行之有效的方法是在合適的模態基礎上增大激勵電壓。通過施加不同峰峰值的交變電壓，頻率為面內四階振動的共振頻率，研究質點位移隨電壓變化情況，如表2所示，定子質點的周向位移與徑向位移隨著電壓的升高呈線性分布，且都具有較大的位移比。

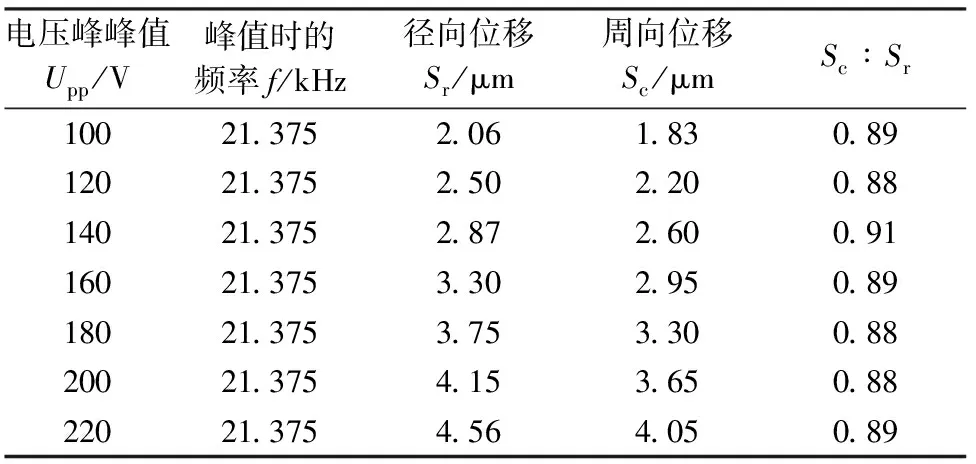
表2 質點位移變化

5 結 語

電機較為理想的工作狀況是電機轉子運轉平穩且電機定子與轉子無相對滑動。實現電機良好運轉，要選擇合適的振動模態，電機定子表面質點應有較大的周向位移和徑向位移，且周向位移和徑向位移之比盡量大。本文研究的是一種中空形行波超聲波電動機，定子的設計一改傳統的結構，定子齒呈錐形，設計新穎，內孔為正十六邊形，不僅便于壓電陶瓷片的粘貼，也有利于中心孔空間的較大利用。

依據實際的需求，并結合理論，進行合理的尺寸設計，選擇模態振型，通過對定子施加不同電壓值進行諧響應分析，證明電機輸出性能較好、隨時可調速度快，以此驗證結構設計的合理性。