陶瓷開裂故障行波型超聲波電動機建模與仿真分析
安國慶,楊少銳,安孟宇,劉慶瑞,閆彩紅,李洪儒
(1.陸軍工程大學,石家莊 050003;2.河北科技大學, 石家莊 050018)
0 引 言
行波型超聲波電動機作為一種新型微特電機,具備斷電自鎖、運行無噪聲、無電磁干擾、微距控制等特點,在航空航天、醫療設施與生物學、光學設備、工業機器人、軍事裝備等領域具有廣泛的用途[1]。壓電陶瓷是超聲波電動機的關鍵元件,當其受到相位差為π/2的兩相交變電壓激勵時,通過逆壓電效應,可在定子上形成行波,并通過定轉子之間的摩擦力使電機轉動[2]。 由于壓電材料的硬脆特性,在長時間高頻電壓的激勵下極易開裂。壓電陶瓷開裂后,將導致機械特性變軟,裂紋的惡化逐漸演變為陶瓷的完全斷裂失效, 大大降低了電機所在系統的可靠性。
隨著維修理論和相關技術的發展,以故障預測技術為核心的基于狀態的維修引起許多專家學者的重視[3]。 行波型超聲波電動機的壓電陶瓷有一個中間正向極化的π/4區域,在電機運行過程中沒有電壓信號,稱為孤極。定子上有行波經過時,孤極區域將會有振動產生,正壓電效應使孤極區域產生孤極電壓信號。電機運行過程中,通常可利用孤極信號反饋來監測定子的振動情況。因此,分析孤極電壓信號隨壓電陶瓷開裂程度的變化規律,可為退化狀態識別過程中的故障特征提取提供有益參考。建立具有壓電陶瓷開裂故障的行波型超聲波電動機定子模型,是準確提取電機壓電陶瓷退化特征的基礎。文獻[4]使用恢復系數(COR)開發了一種動力學模型來模擬定子和轉子之間的正常沖擊;文獻[5]利用有限體積法(FVM)的離散二維方程組建模,測出電機在直流和交流電壓作用下的定子響應;文獻[6]通過ANSYS定子建模得到了當定子接觸尖端的振幅明顯增大時,有助于提高電機驅動力和轉速的規律。文獻[7]設計了基于模糊邏輯的辨識建模方法,建立了超聲波電動機系統動態模糊模型。文獻[8]將有限元法應用于被裂縫削弱的二維壓電介質,然后用四倍標準壓縮函數來評估強度因子;文獻[9]利用等距擴展分析(XIGA)模擬了壓電材料在動態和靜態耦合下的二維斷裂力學問題;文獻[10]采用縮放邊界有限元法(SBFEM)分析了多孔壓電固體中的裂紋,在數值分析中考慮了裂紋空隙解決了邊界值問題。從近期文獻來看,關于行波型超聲波電動機定子壓電陶瓷開裂的仿真研究較少。
本文擬建立不同開裂程度的故障模型,并通過有限元分析,得到定子孤極電壓信號隨壓電陶瓷裂紋擴展的變化規律。并利用實測信號與仿真結果進行對比,以驗證壓電陶瓷開裂建模方法的正確性和合理性。
1 電機運行的數學描述
1.1 行波型超聲波電動機運行機理分析
對定子壓電陶瓷上的A,B區域分別施加交變電壓,交變電壓的頻率相同,幅值相等,相位差為π/2。根據壓電陶瓷的逆壓電效應,定子上將會產生2個幅值相等、空間與時間相位差為π/2的駐波,2個駐波經過疊加在定子環中產生沿定子圓周運動的行波。行波利用定子表面的水平運動來驅動轉子旋轉[11-13]。
壓電陶瓷層的圓環分為A區和B區,A和B之間的空間相移是波長的四分之一[14],如圖1所示。
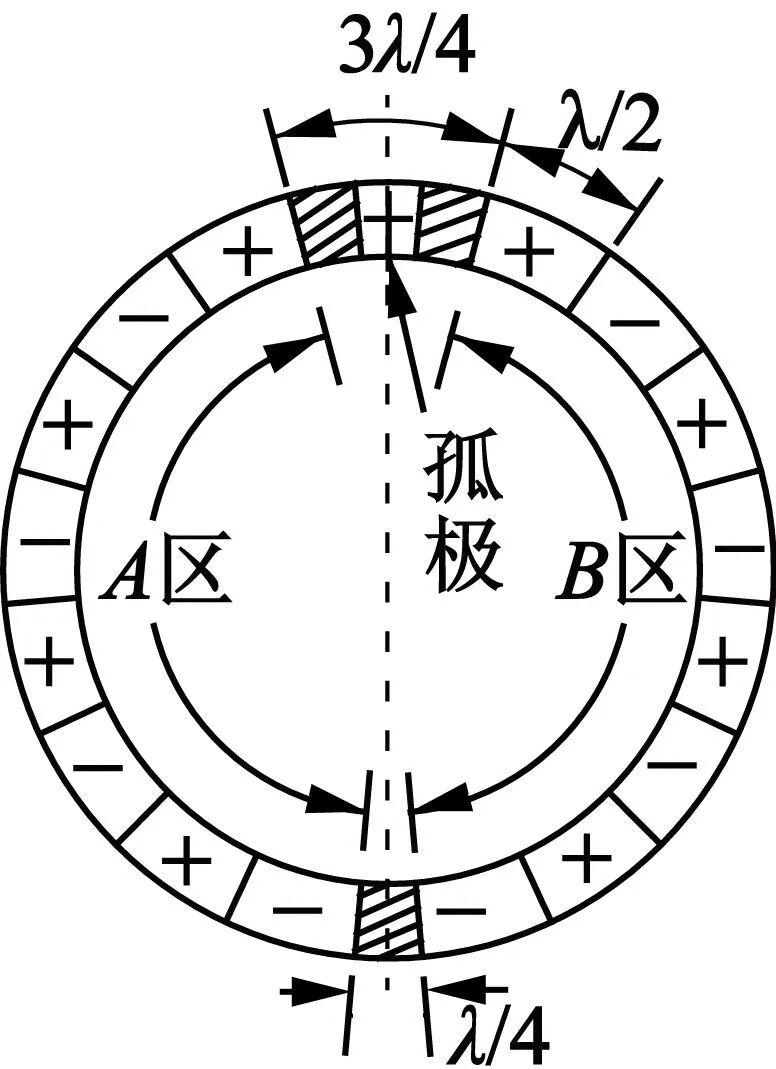
圖1 壓電陶瓷的極化分割
當兩相交變電壓同時施加在A區和B區上時,定子表面垂直方向的振動位移分別:
ωA(x,t)=ξAcos(kx)cos(ωt+θL)
(1)
ωB(x,t)=ξBcos[k(x-λ/4)]cos(ωt+θL+φ)=
ξBsin(kx)cos(ωt+θL+φ)
(2)
式中:ξA,ξB為振幅;λ為波長;k為彈性波的波數;θL為初始相位角;φ為相位差。
在定子圓周兩相駐波疊加后的定子位移響應:
ω(x,t)=ωA(x,t)+ωB(x,t)=
ξAcos(kx)cos(ωt+θL)+
ξBsin(kx)cos(ωt+θL+φ)
(3)
當壓電陶瓷環對稱極化時,令:ξA=ξB=ξ。
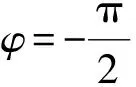
ω1(x,t)=ξcos(kx-θL-ωt)
(4)
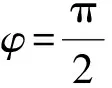
ω2(x,t)=ξcos(kx+θL+ωt)
(5)
因此,通過改變兩相激勵信號的相序可改變電機的旋轉方向。
1.2 壓電陶瓷開裂對孤極信號的影響
假設定子表面任意一點為P,當在定子中產生行波時,橫截面旋轉角度為γ,如圖2所示。
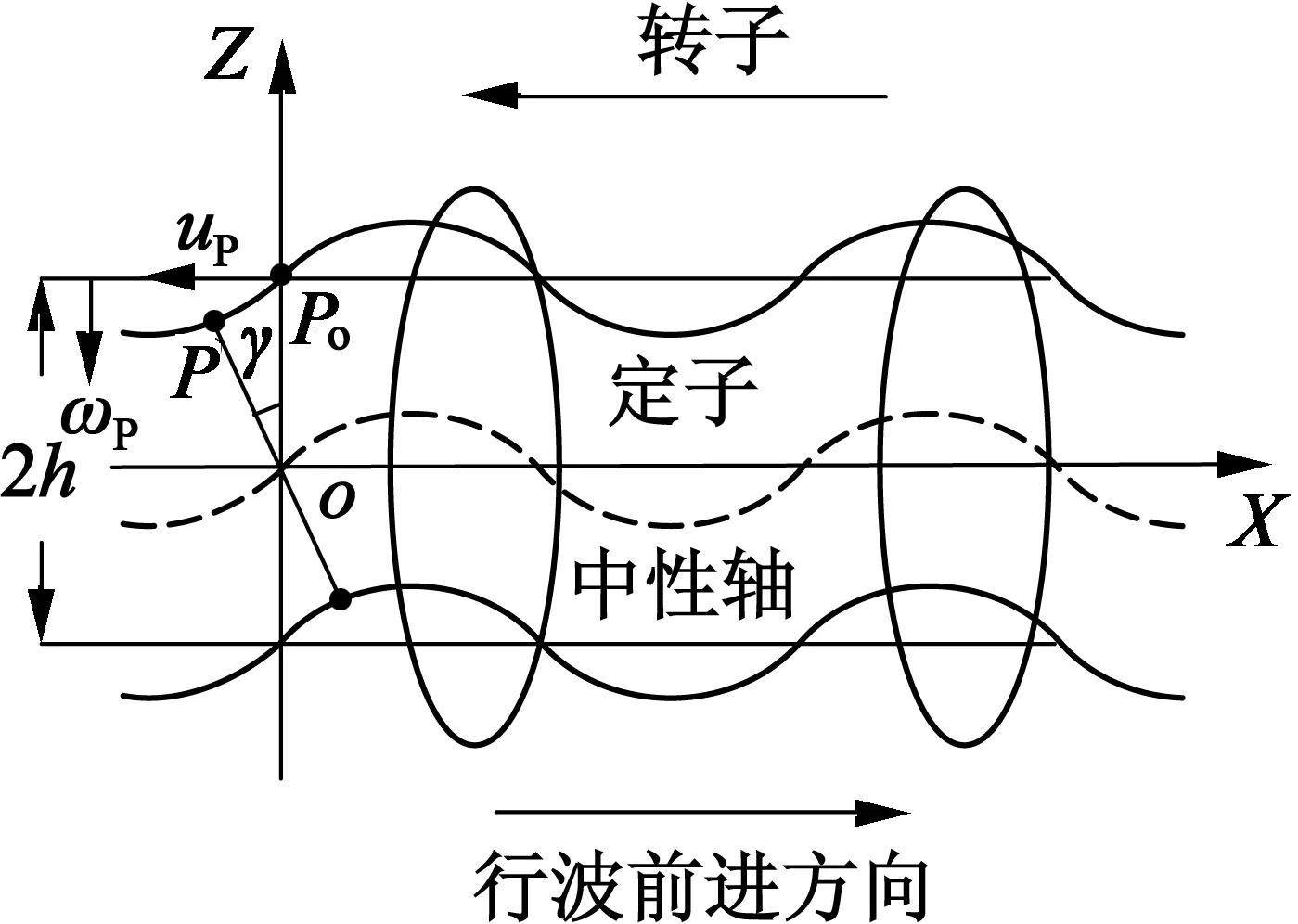
圖2 行波運動圖像
當P移至P0位置時,在Z方向和X方向的位移分別:
ωP(x,t)=ξcos(kx-ωt)-h(1-cosγ)
(6)
uP=-hsinγ
(7)
式中:ξ為Z方向對應的幅值;h為定子表面質點距行波中性層的距離。由于γ非常小,由P至P0在Z方向和X方向的位移可簡化:
ωP(x,t)=ξcos(kx-ωt)
(8)
uP=-hγ
(9)
(10)
將式(10)代入式(9)得P至P0點X方向的位移:
uP=-hγ=kξhsin(kx-ωt)
(11)
結合式(8)與式(11),可得定子表面任意一點P在Z方向和X方向的位移之間的關系:
(12)
可見,定子表面任意質點P的運動軌跡為橢圓。壓電陶瓷開裂后,裂紋處無壓電晶體的逆壓電效應,這將對兩相駐波合成的行波產生影響,導致其機械特性變軟。對于孤極區域的質點而言,陶瓷開裂后會影響整個壓電陶瓷的共振特性,導致Z方向和X方向的振動位移都減小。由式(8)可知,與壓電晶體表面垂直的Z方向的振動幅值ξ減小,因此孤極區域質點運動的橢圓軌跡Z幅值減小。由于壓電晶體正壓電效應中,垂直壓電陶瓷片的振動分量才會產生電信號,因此孤極區域的電信號將隨之減小。
2 行波型超聲波電動機定子的有限元分析
2.1 超聲波電動機定子有限元建模
(1) 定義單元類型及材料參數
超聲波電動機定子為三維實體結構,網格劃分采用六面體單元,壓電陶瓷的材料為PZT-4,定子彈性體的材料為黃銅。分別在預處理器中定義材料壓電陶瓷與金屬彈性體的密度、彈性模量、泊松比等參數,參數如表1所示。

表1 超聲波電動機相關材料參數
壓電陶瓷的介電矩陣:
壓電陶瓷的壓電矩陣:

壓電陶瓷的剛度矩陣:
(2) 定子建模
電機定子尺寸如表2所示。

表2 電機尺寸表
表2中,hm為定子金屬彈性體高度;ht代表定子齒高;hp代表壓電陶瓷厚度;r1代表定子內半徑;r2代表定子外半徑。電機定子橫截面如圖3所示。
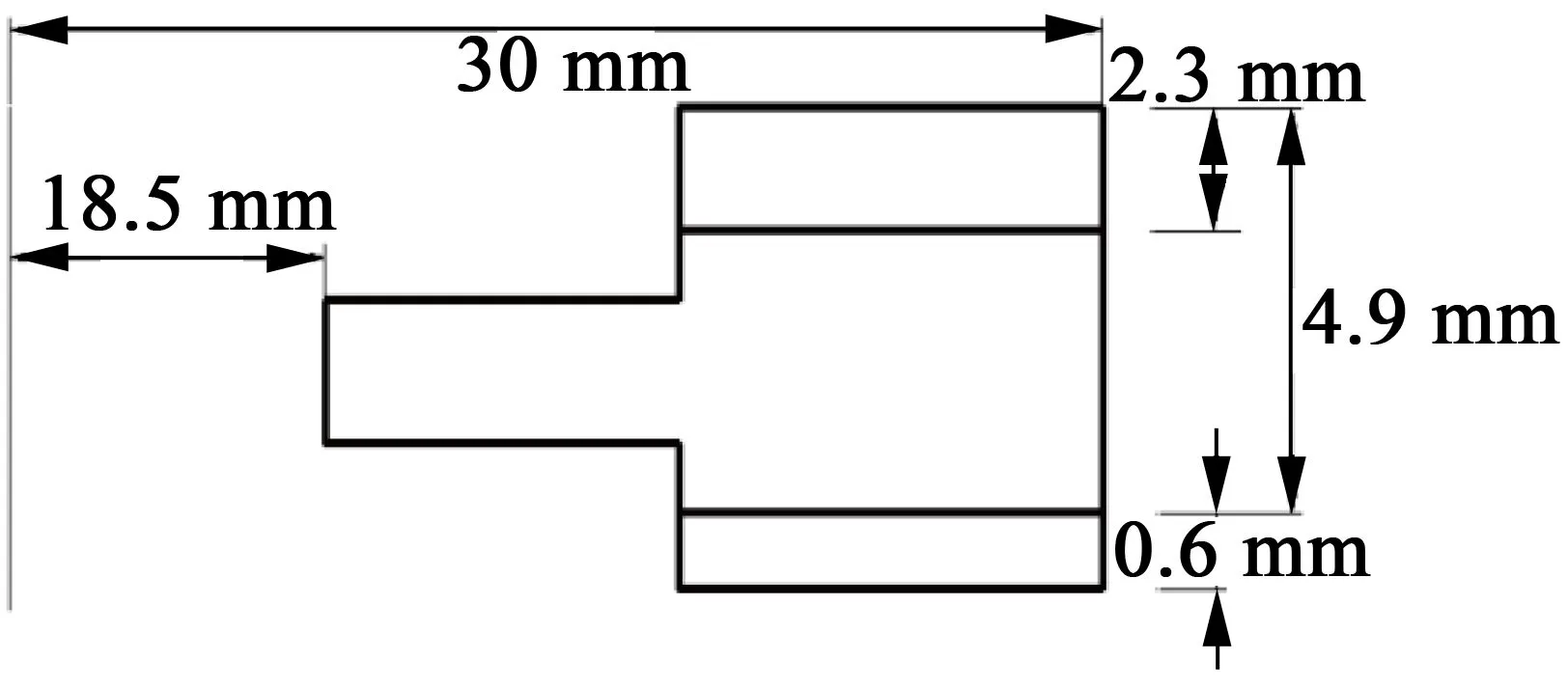
圖3 電機定子橫截面圖
電機共有72個齒,齒槽比為3∶4∶4,建立超聲波電動機定子的實體模型,如圖4所示。

圖4 超聲波電動機定子實體模型
(3) 有限元剖分
通過網格劃分定子的橫截面,對單體采用掃掠剖分,將齒按照2∶3∶4劃分為24個單元,基體上半部分按3∶4∶4劃分為48個單元,下半部分按1∶4∶2劃分為8個單元,壓電陶瓷片按1∶4∶4劃分為16個單元。超聲波電動機定子單體剖分模型如圖5所示,超聲波電動機定子的有限元分析模型如圖6所示。

圖5 單體的剖分模型

圖6 定子有限元模型2.2 定子模態分析
定子模態分析的頻率范圍在20~100kHz之間,擴展40階模態進行分析。定子模態分析結果(未全列出)如表3所示。

表3 定子模態結果
對于行波型超聲波電動機,過高的模態階數會使壓電陶瓷內部與定子的機械損耗增多,會降低定子的振動幅度。通過考慮兩相對稱原則以及增加定子可激發區域的利用率,超聲波電動機應進行奇數模態的分析。綜合以上原因,選擇模態B09作為超聲波電動機的工作模態,其共振頻率為34 395Hz,B09模態時壓電陶瓷的對應彎曲振型圖如圖7所示。

圖7 B09模態彎曲振型圖
2.3 諧響應分析
正弦電勢載荷施加在定子的壓電陶瓷電極上面,施加在正向極化區域和反向極化區域上的電勢載荷的相位差為π/2,壓電陶瓷的另一面的電壓設置為0。施加的載荷可表示:
式中:Φ表示節點處電壓值;hp表示壓電陶瓷片的厚度大小;f表示激勵電壓頻率大小;U0表示激勵電壓幅值大小;z=0代表壓電陶瓷上表面;z=-hp代表壓電陶瓷下表面。B09模態下定子的振動頻率為34 395Hz,輸入電壓幅值為100V,選擇在工作模態頻率附近的32 000~35 000Hz范圍內進行諧響應分析,諧響應分析結果如圖8所示。由圖8可知,定子振動幅值在34 510Hz處取得最大值。

圖8 正常電機諧響應分析
2.4 孤極質點瞬態分析
采用Full法, 取孤極區域某一質點進行瞬態分析。諧波激勵電壓的有效值為100V,激勵電壓頻率由諧響應分析獲得,激勵電壓頻率為34 510Hz,周期T=2.9×10-5s, 孤極區域某一質點在0.001s內瞬態分析結果X,Z方向的位移響應曲線分別如圖9所示。
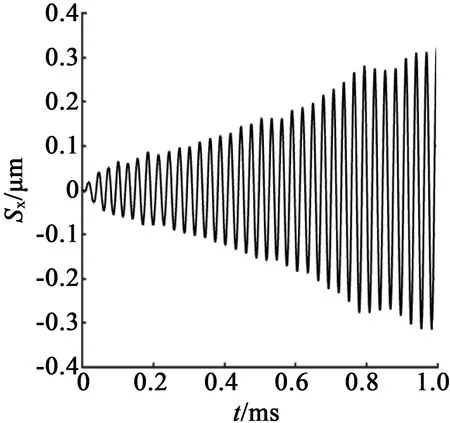
(a) X方向位移

(b) Z方向位移
為了更加明確分析結果,繪制出質點X,Z方向隨時間變化的位移運動軌跡,如圖10所示。

圖10 無故障電機質點運動軌跡
結果表明,定子表面質點在X方向和Z方向上均做諧波振動,兩者合成一個橢圓運動軌跡。仿真結果與理論分析吻合,證明無故障電機定子建模方法是合理可行的。
3 壓電陶瓷開裂故障仿真分析
在壓電陶瓷區域內,存在固定數目的小單元。通過刪減小單元不同數量的方式來模擬壓電陶瓷不同的開裂缺損程度。分別去掉1,2,4小塊單元模擬陶瓷片輕度,中度,重度開裂情況。輕度開裂的裂紋大小為0.33mm×1.875mm×0.6mm, 中度開裂的裂紋大小為0.33mm×3.75mm×0.6mm,重度開裂的裂紋大小為0.33mm×7.5mm×0.6mm,對應故障的定子模型如圖11所示。
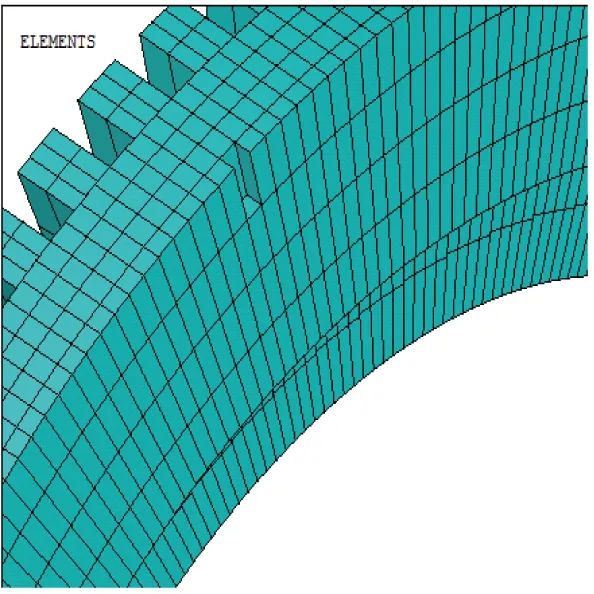
(a) 輕度開裂
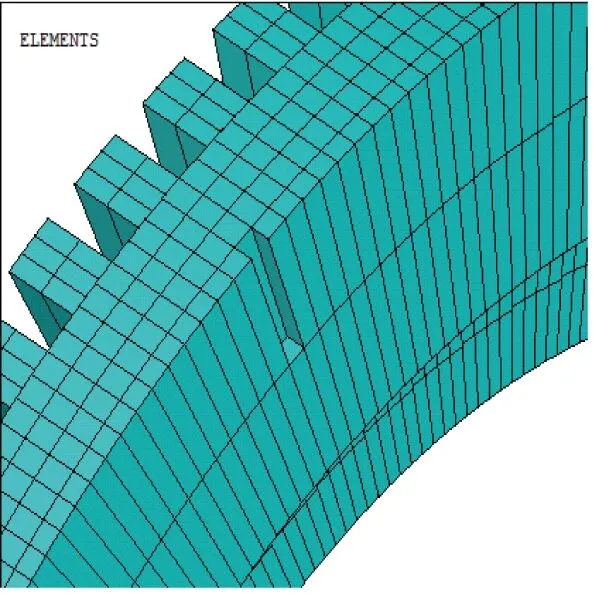
(b) 中度開裂
(c) 重度開裂
電機施加諧振頻率34 510Hz,對故障程度依次增加的電機模型進行瞬態響應分析。取電機孤極區域上同一質點進行瞬態響應分析,得到該質點的運動軌跡,如圖12所示。
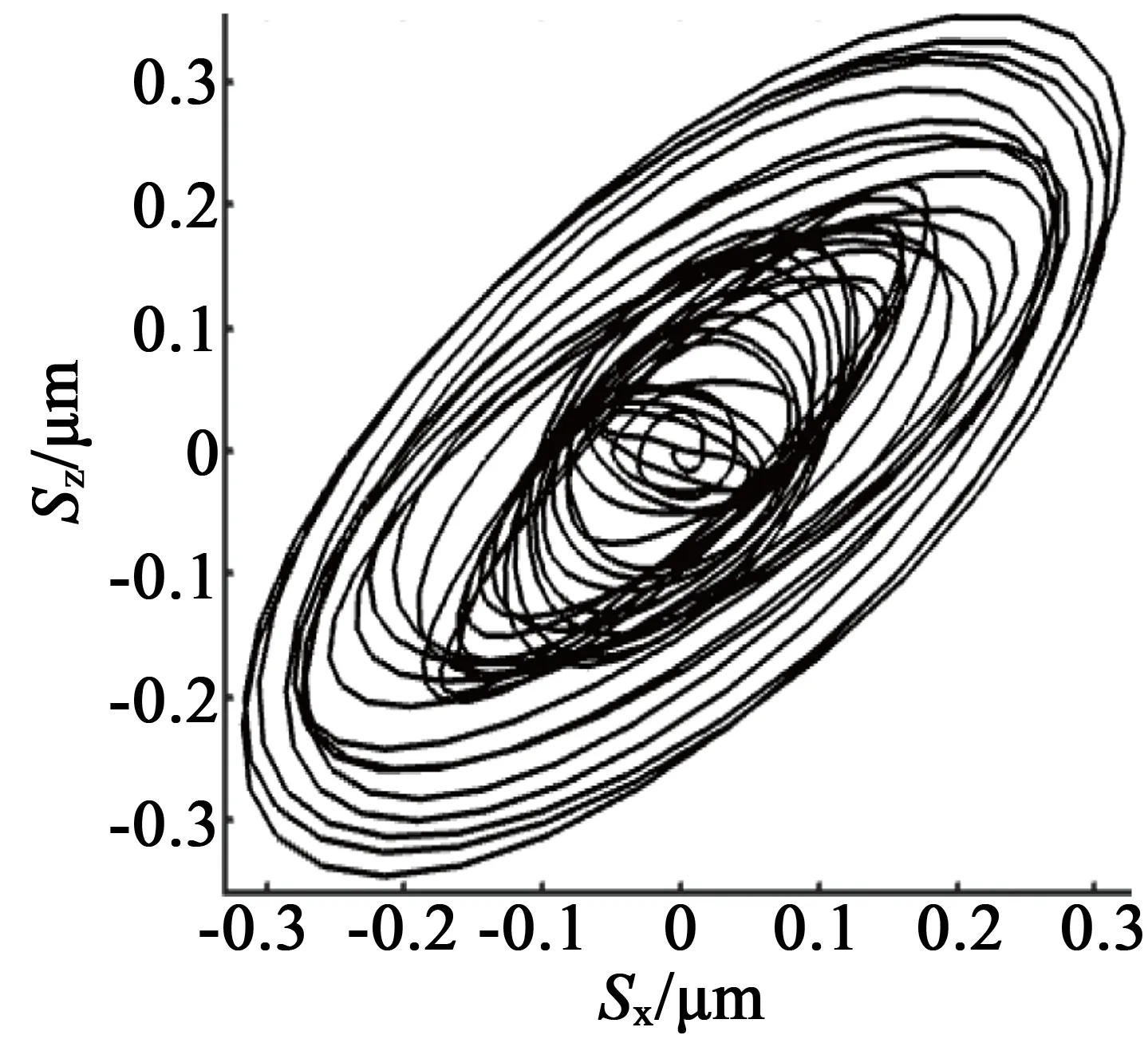
(a) 無故障

(b) 輕度開裂
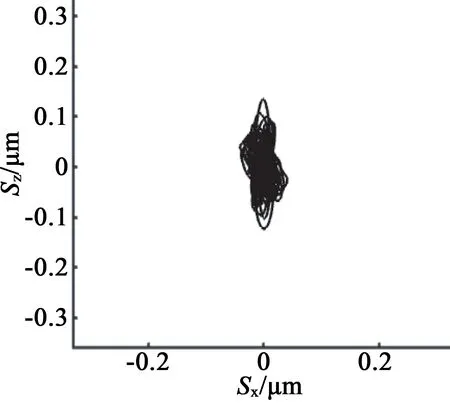
(c) 中度開裂
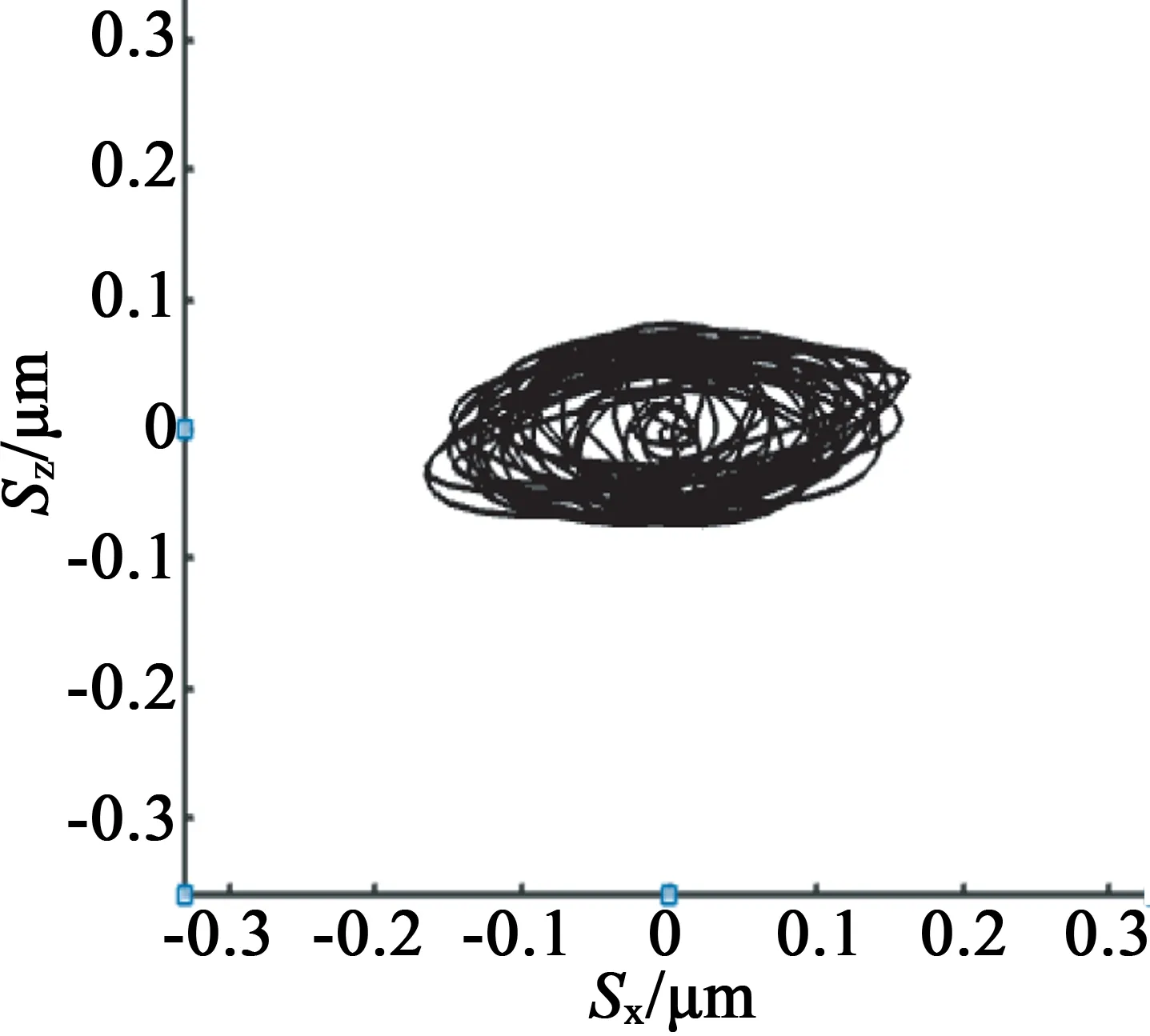
(d) 重度開裂
圖12統計的質點Z方向幅值變化如表4所示。

表4 超聲波電動機振動軌跡Z方向幅值
可見,超聲波電動機壓電陶瓷出現開裂時,3個電機模型相同質點的橢圓軌跡都發生了不同的變化,隨著開裂程度的增加,Z方向振動幅度呈減小趨勢。
該質點壓電效應產生的電壓信號時域變化如圖13所示。
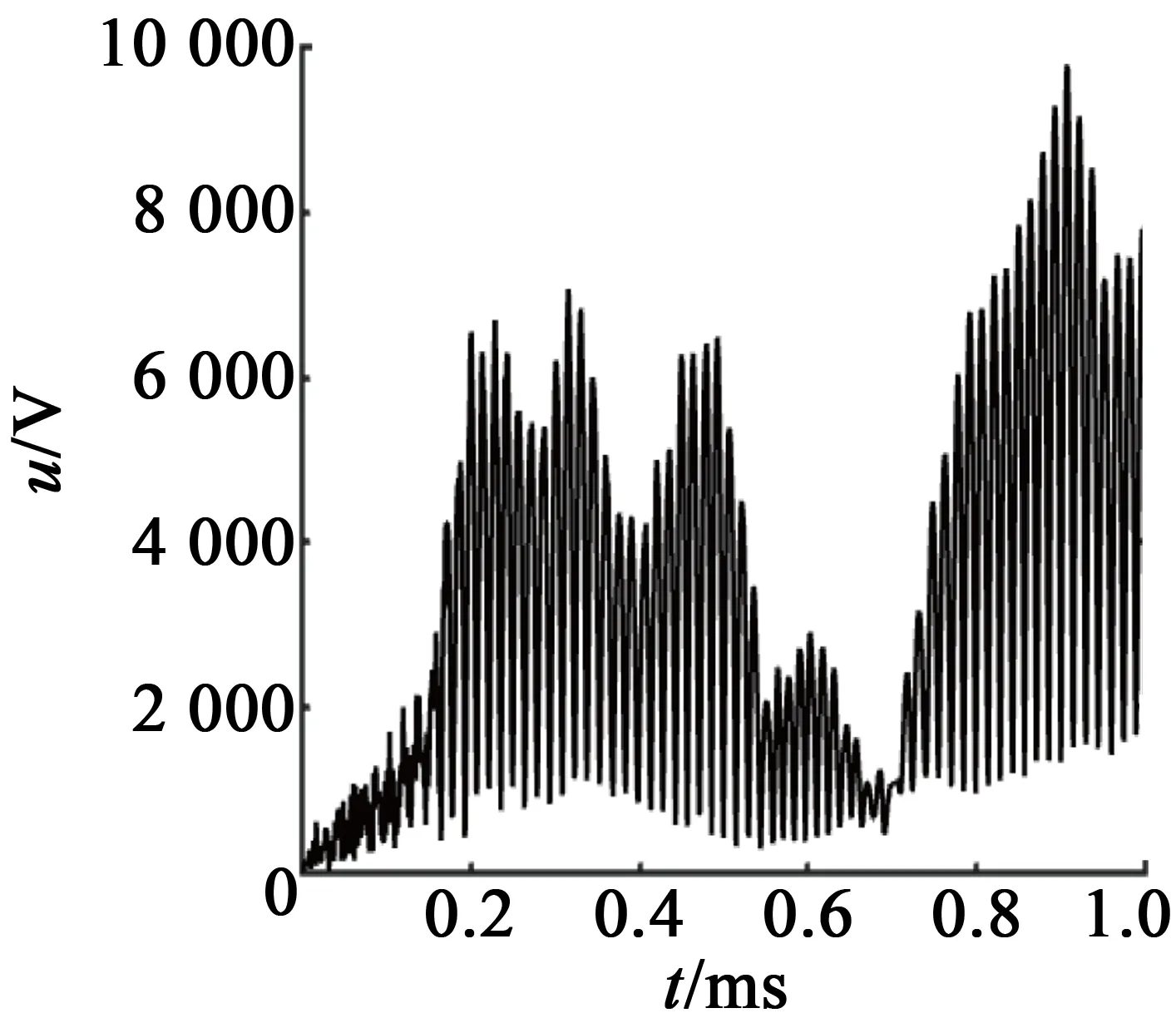
(a) 無故障

(b) 輕度開裂

(c) 中度開裂
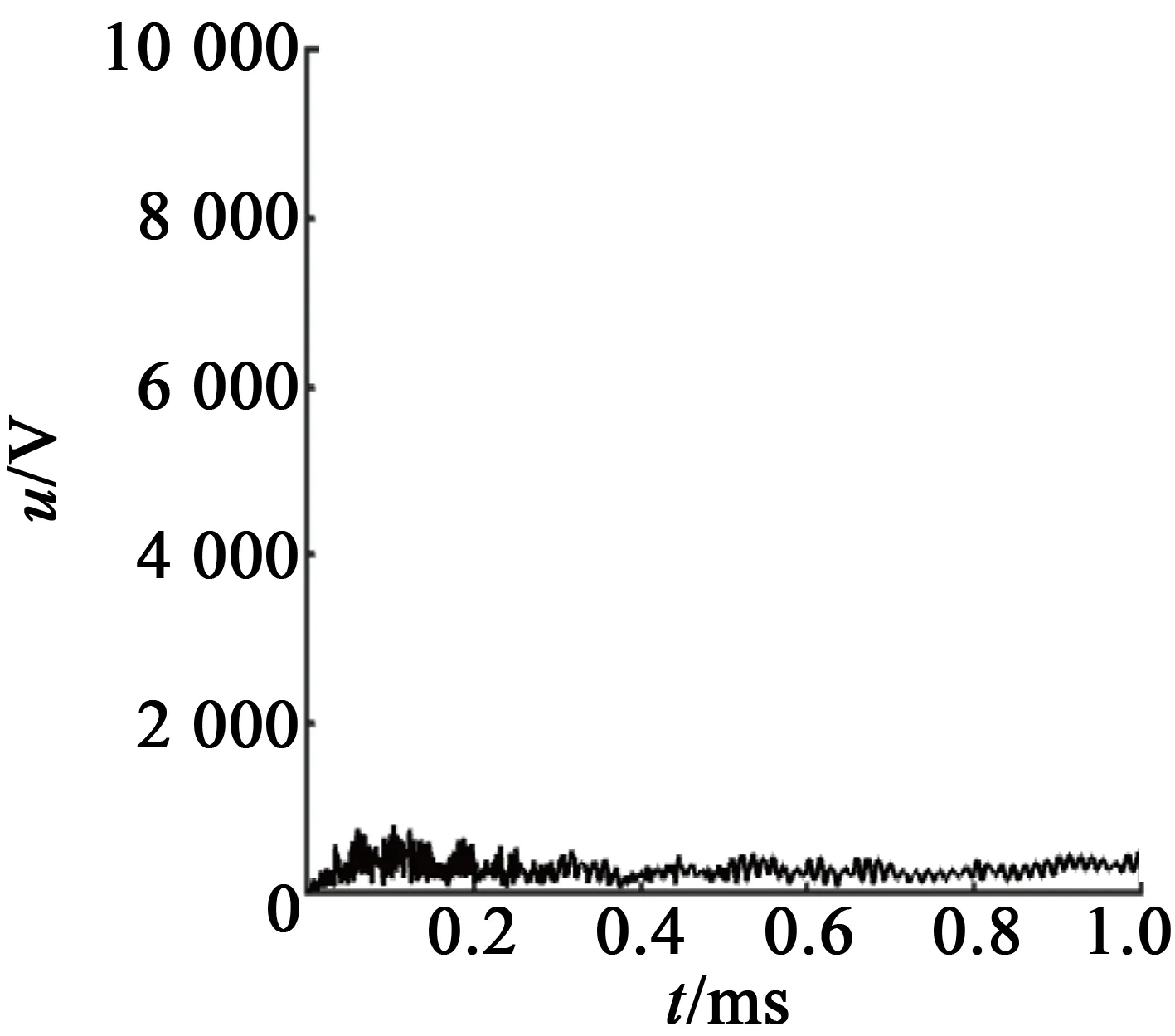
(d) 重度開裂
以上電壓信號的頻譜分析結果如圖14所示。
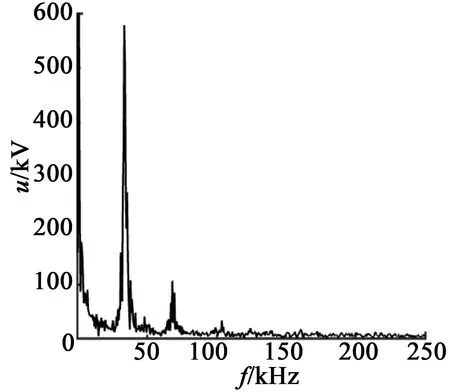
(a) 無故障

(b) 輕度開裂

(c) 中度開裂

(d) 重度開裂
各故障頻譜序列中電機驅動頻率下孤極區域質點電信號大小的統計結果如表5所示。

表5 超聲波電動機特定頻率下電信號變化
統計結果表明,在驅動頻率下孤極區域質點電信號,隨壓電陶瓷開裂程度的加大呈下降趨勢。
4 壓電陶瓷開裂故障實測信號分析
選取型號為GTUSM-60的行波型超聲波電動機進行孤極電壓實測信號分析。3個定子樣本分別是正常,輕度開裂,重度擊穿,具體情況如圖15所示。

(a) 無故障

(b) 輕度開裂

(c) 重度擊穿
分別加載頻率為40.65 kHz的驅動信號,在電機空載的狀態下,利用Handyscope HS4高速數據采集卡進行孤極電壓信號采集,采樣頻率為500 kHz。孤極電壓時域波形如圖16所示。
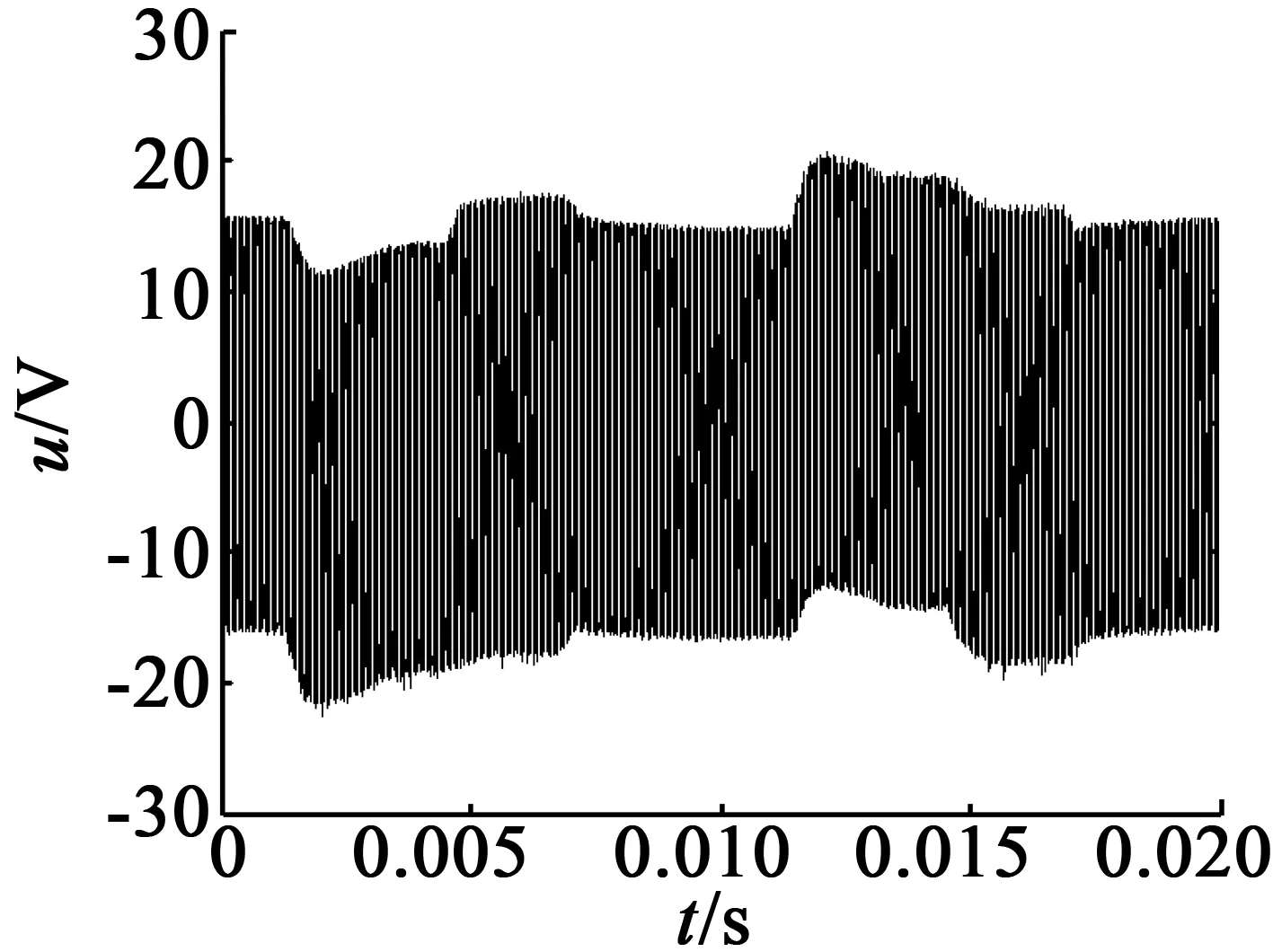
(a) 無故障
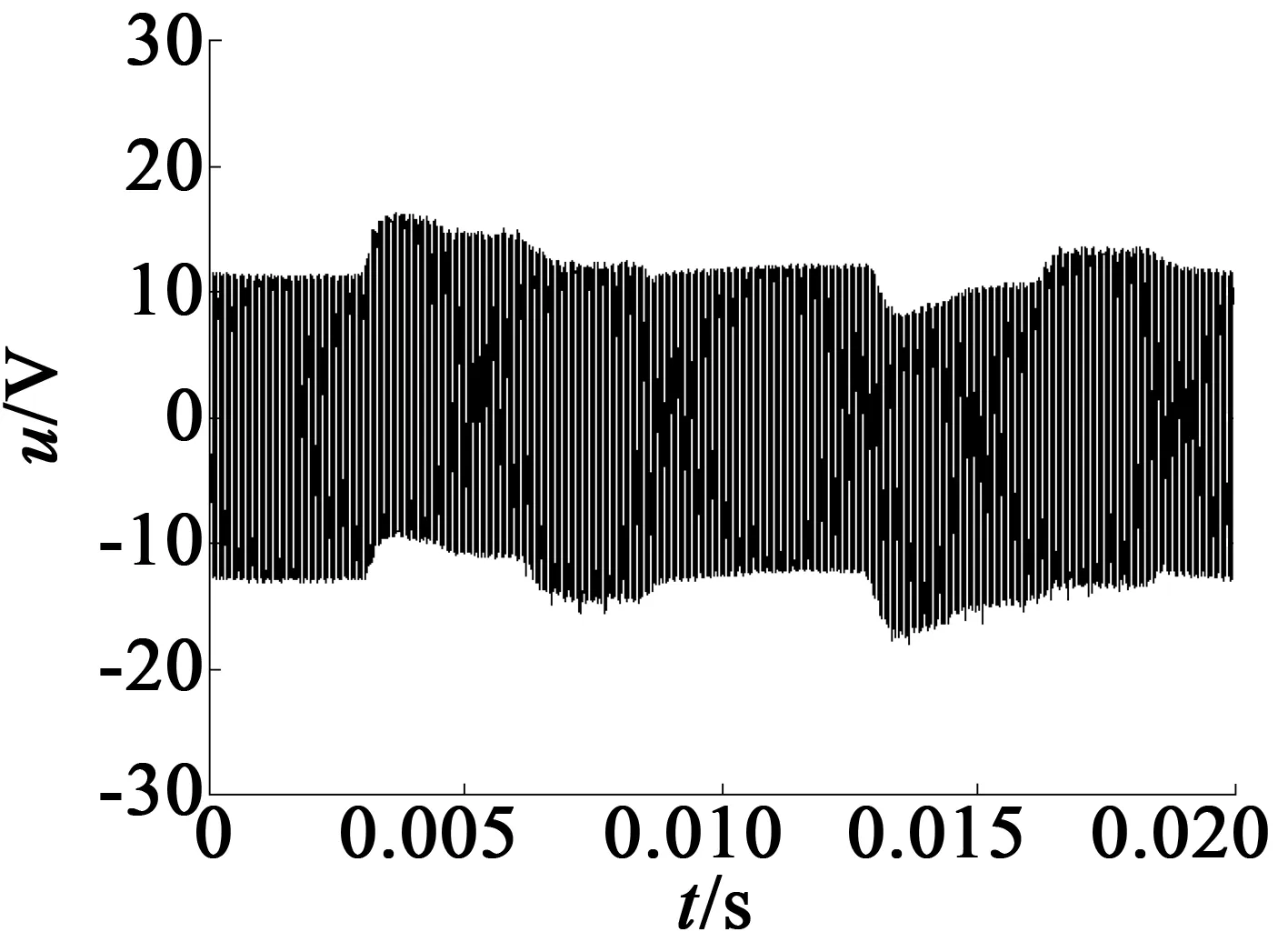
(b) 輕度開裂
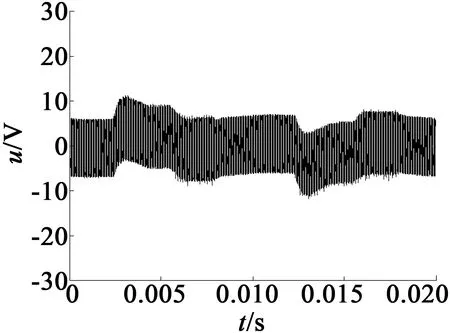
(c) 重度擊穿
實測孤極電壓信號的頻譜分析結果如圖17所示。

(a) 無故障
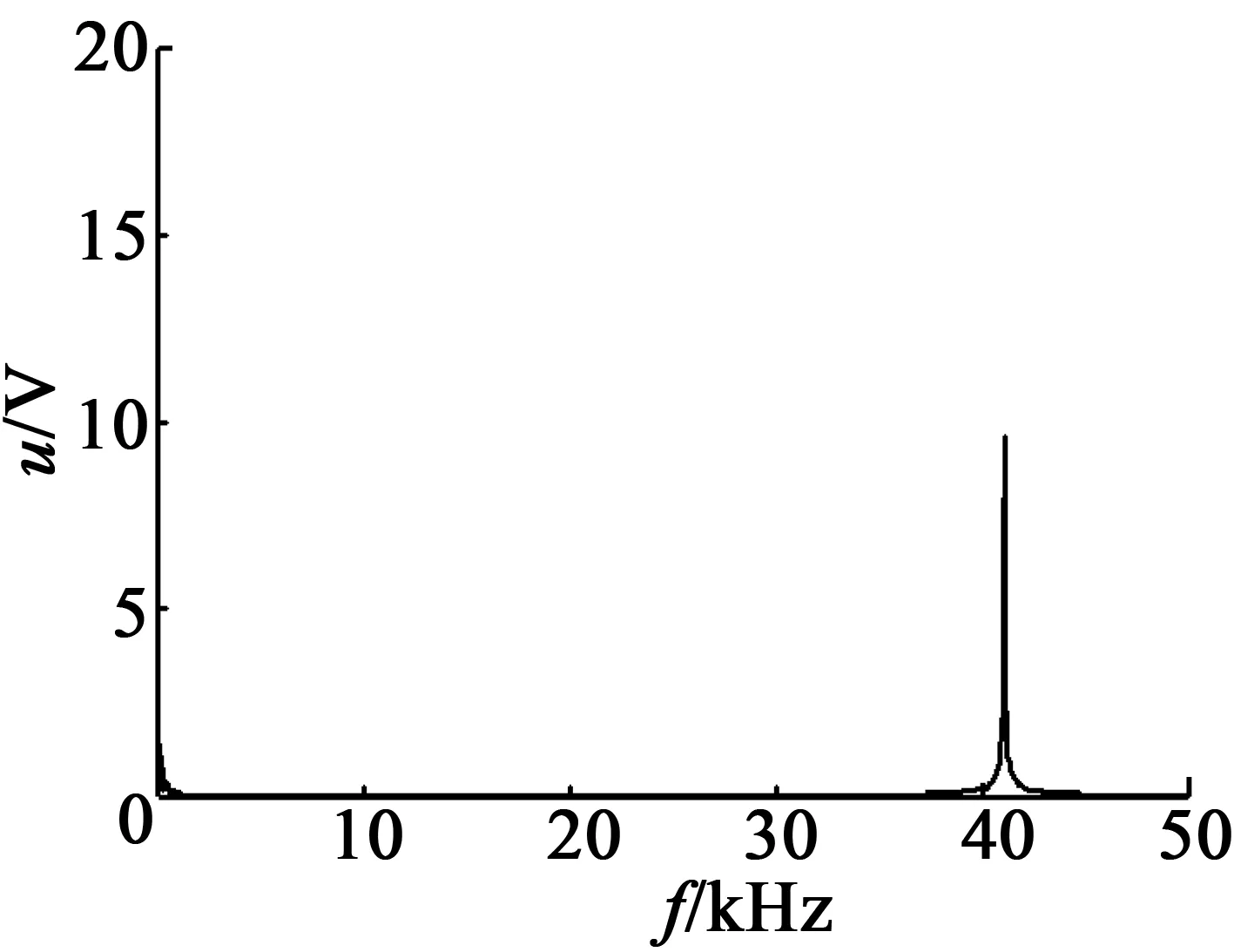
(b) 輕度開裂

(c) 重度擊穿
實測孤極電壓信號的分析結果如表6所示。由表6可以看出,隨著壓電陶瓷開裂程度的增加,孤極電壓信號也呈減小趨勢。

表6 實測孤極電壓信號變化
5 結 語
對建立的行波型超聲波電動機定子限元模型進行了動力學分析,其9階模態的瞬態響應仿真結果表明,電機定子質點的運動軌跡為橢圓,符合理論分析,驗證了建模方法的可行性。
通過徑向刪減剖分單元的方法模擬壓電陶瓷的不同開裂程度。電機瞬態響應仿真結果表明,當裂紋擴展時,電機定子質點橢圓運動軌跡Z軸方向幅值將逐漸減小。符合理論分析,模擬壓電陶瓷開裂的建模方法可行。
對行波型超聲波電動機模型上的孤極電壓仿真信號進行頻譜分析。仿真結果表明,隨著開裂程度的增加,孤極電壓幅值和諧振頻率分量幅值都呈下降趨勢。型號為GTUSM-60電機在壓電陶瓷不同開裂程度下,孤極電壓實測信號的變化趨勢與仿真結果吻合,驗證了本文建模仿真方法的合理性。

