打破思維定勢 激發創新思維

朱紅芳

蘇州市吳江區北厙中學 江蘇蘇州 215200

古語云“文無定法，思無定式”，數學傳統的教學方法過多地強調了老師講的程式，學生按部就班解題，這對于初學者來說不失為一種入門法，但無形中也給學生劃定了一個框架，束縛了學生的思路，學生碰到“變式題”，只能望題興嘆，陷入思維定式的陷阱。要改變這種狀況，老師必須強化輔導環節，根據學生實際思維水平設計教學內容，重點放在如何開拓思路上，多給學生留下思維的空間，培養良好的思維品質，營造思維的綠洲。

一、培養思維的探索性

蘇霍姆林斯基說過：“在人們的心靈深處，都有一種根深蒂固的需要，這就是希望感到自己是一種發現者、研究者。”數學基礎比較好的學生，老師可以根據教學內容巧設疑難，加以適當的啟發后讓學生觀察、思考、分析、對比，養成探索的習慣，提高探索的興趣。

我在教因式分解的拆項、添項法時，先布置這樣一道題“分解因式：1、x2-y2-z2-2yz；2、x3-2+2x2-x；3、x3-2x2+3”其中第“3”題學生無法可想，我引導學生在公式法中想辦法，（a +b）2展開式為什么是三項，（a+b）(a-b)的積為什么是二項，讓學生領會并項與逆向的拆項。于是就有學生提出將其中的一項拆為兩項，再找分組的可能性，將“-2x2”項拆為-3x2+x2或者-4x2+2x2等等，啟發他們對拆法提出要求。并問：有規律嗎？“x3”這項能拆嗎？“+3”這項能拆嗎？讓他們找出拆法；接著我指出缺項系數是0，把這項0拆就成了添項，讓學生思考：這里能否用添項的辦法？添上3x-3x是否使它具有分組條件？添上4x-4x行否？添項時要注意什么？最后，學生能根據多項式x4+4的特征，采用添項法分解因式。

二、培養思維的靈活性

義務教育數學大綱指出，初中數學中辯證唯物主義教育的一個因素是“數學內容中普遍存在的運動變化、相互聯系、相互轉化等觀點”，要求培養學生的觀察能力，類比分析、綜合串聯的能力。作為教師，也應培養學生用運動變化、尋找聯系、相互轉化的觀點來思考問題，這就是培養思維的靈活性，做法是觀察、聯想、轉化，從內在聯系得到求解的方法。

例如，蘇科版教材七年級下冊“期末復習全等三角形”時，我設計了如下的例題：如圖1，已知點C是線段BE上的一點，△ABC，

△CDE都是等邊三角形，求證

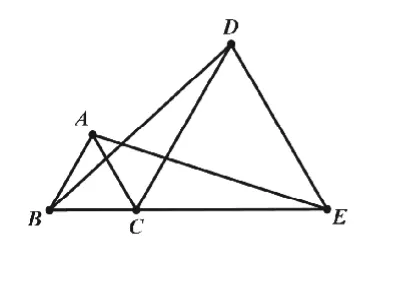
圖1

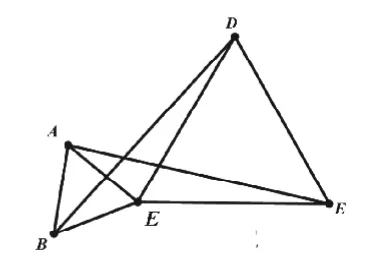
圖2

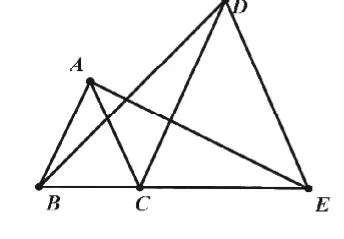
圖3

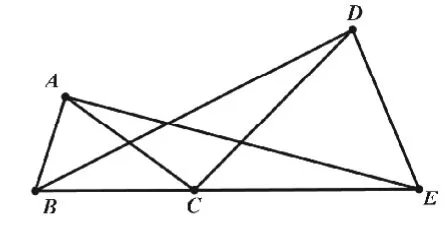
圖4

【變式1】如圖2，將△CDE繞點C按順時針方向旋轉角后，以上結論是否成立？為什么？

【變式2】將等邊三角形改為等腰三角形，結論成立嗎？學生展開了以下討論：

（1）結論不成立。以BC、CE為底的等腰三角形（如圖3）

（2）結論成立。以BC、CE為底的等腰三角形（如圖4）

這樣設計問題具有變通性，它有助于學生抓住問題的本質，從中尋找他們之間的內在聯系，探索出一般規律，從而提高學生的思維品質。它有助于激發學生探索問題的興奮點，讓學生在解開放性問題的過程中對問題從不同角度進行探索，從不同層面進行分析，克服思維定勢，避免思維僵化，從而有助于全面深刻地認識問題，靈活多樣地處理問題，它能較好地培養學生思維的靈活性。

三、培養思維的周密性

思維具有周密性，才能全面地看問題，才能既綜觀全局，又不忽略重要的細節。初中學生開始從幼稚向成熟過渡，他們的思維情感在發生變化，經驗閱歷又不足，對所學知識的全面理解也不夠，于是在研究較復雜的問題時，常難于深入全面地分析問題，不能透過現象抓本質。為改變這種情況，應先讓學生探索問題，然后把學生的思維活動展開，針對學生分析上存在的缺陷進行引導，讓學生去抓住事物本質規律去作出周密的思考。

在具體教學中，連續地構造知識系統，使新獲得的知識和技能納入學生原有的知識系統，以保持思維的周密性。學“圓”這部分知識時，學生感到知識點多、很零亂，教師給予適當點撥。圓是三角形、四邊形與它的知識的有機結合，是初中幾何達到了最精彩的部分，例如三角形與圓的結合：圓內接三角形的外心就是外接圓的圓心；圓外切三角形的內心就是內切圓的圓心；圓內接正三角形的邊長與外接圓的半徑之比為根號3比1。又如四邊形與圓的結合：圓內接四邊形的對角互補，圓內接梯形一定是等腰梯形，圓內接平行四邊形一定是矩形；圓的外切四邊形的兩組對邊的和相等。通過這樣的點撥，使前后知識融為一體，使知識系統化，溫故而知新，培養了學生思維的周密性。

四、培養思維的創造性

當前初中數學教學進行素質教育的一個重要方面就是培養學生的創造思維能力。初中學生研究問題習慣于按照常規思考，受定向思維約束，對有些關系隱含、曲折的問題常會感到無計可施。教師在帶領學生對問題進行探索時，應引導學生擺脫原有知識范圍的羈絆和定向思維的制約，利用題中隱含的條件，把頭腦中已有的知識信息重新組合，發現新問題，標新立異，另辟捷徑。

在例題教學上，要適當運用變式，講究逐步設置障礙，不斷增加創造性因素，達到舉一反三的目的。例如，如圖5，△ABC各邊長都大于2，分別以A、B、C為圓心，以1為半徑畫圓，求陰影部分的面積。

分析：我們可以讓學生把三個陰影部分剪下來，重新拼圖，從而就可以得到一個半徑為1的半圓，故陰影部分的面積為

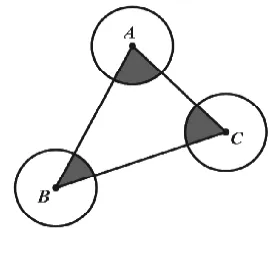
圖5

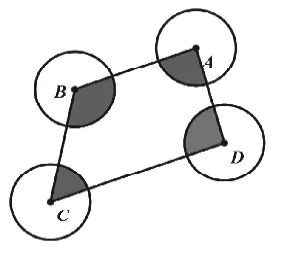
圖6

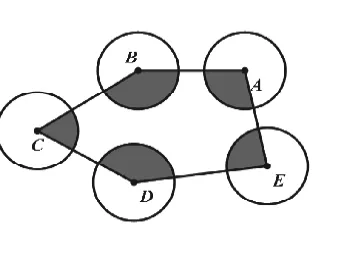
圖7

對于這道題，如果我們就此結束的話，并不能引起學生的共鳴。我們可以對這個問題進一步探索：

【變式一】如圖6，把題目中的△ABC換成四邊形ABCD，其他條件不變，求陰影部分的面積。

分析：重新拼圖，從而就可以分別得到一個半徑為1的圓，故陰影部分的面積為。

【變式二】如圖7，把題目中的△ABC換成五邊形ABCDE，其他條件不變，求陰影部分的面積。

分析：重新拼圖，從而就可以分別得到一個半徑為1的圓和一個半圓，故陰影部分的面積為。

【變式三】把題目中的△ABC換成n邊形，其他條件不變，求陰影部分的面積為。

分析：經過前面兩個變式題的理解，我們可以掌握一般性的規律，將陰影部分剪下來，重新拼圖可以得到幾個圓，用的圓，然后再乘以 ，則陰影部分

【評注】本題是從具體的情況入手，如此下去，猜想第n次的結果，這樣讓學生感受從特殊到一般的轉換，或感受從平面到空間的轉換，讓學生去感知知識的再現過程，這樣有利于培養學生的綜合解決問題的能力，充分挖掘學生的潛力，培養學生猜想、歸納能力，更有利于培養學生綜合能力，使學生的綜合素質有較大的提高。這樣的變式，遵循了循序漸進的原則，使學生一步一個臺階，體會到成功的喜悅，極大地激發了學生的積極性、創造性。

綜上所述，要打破學生一貫的思維定式，開創異彩紛呈的數學教學新局面，必須鼓勵學生求新、求異、求變，樹立他們的創新意識，學會一題多思，一題多解，多角度的思維方式，拓寬學生思路，營造思維的綠洲。