高層建筑施工模擬豎向壓縮變形基本原理分析

白 潔 雷 克 葛 杰 孫學鋒 鮑 旺

中國建筑第八工程局有限公司 上海 200122

高層建筑是逐層施工完成的，其豎向剛度和豎向荷載（如自重和施工荷載）也是逐層形成的。這種情況與結構剛度一次形成、豎向荷載一次施加的計算方法存在較大差異[1-2]。因此，JGJ 3—2010《高層建筑混凝土結構技術規程》中第5.1.9條明確規定：高層建筑結構在進行重力荷載作用效應分析時，柱、墻、斜撐等構件的軸向變形宜采用適當的計算模型考慮施工狀態的影響；復雜高層建筑及房屋高度大于150 m的其他高層建筑結構，應考慮施工狀態的影響[3]。

考慮施工狀態與一次性加載計算得到的結構內力、位移均不同。以豎向壓縮變形為例，即使不考慮混凝土的收縮徐變等與時間相關的因素，一次性加載及考慮施工狀態得到的各樓層的豎向位移曲線的典型形狀也有明顯不同（圖1）[4]。由圖1可知，一次性加載的豎向壓縮變形從結構底部到頂部逐漸增大，最大值在結構頂部；而考慮施工狀態的豎向壓縮變形從結構底部到頂部先增大再減小，最大值在結構中部，二者存在顯著差異。上述2種計算方法得到的結構豎向壓縮變形的不同導致了以下2項分析結果的差異：核心筒與外框架豎向壓縮變形差、豎向構件壓縮變形預調值。

核心筒與外框架豎向壓縮變形差直接影響樓面水平度及伸臂桁架的內力；豎向構件壓縮變形預調值直接決定了竣工后結構的標高是否符合設計要求。因此，對高層建筑進行施工過程模擬分析很有必要。

圖1 豎向壓縮變形曲線

目前針對考慮施工狀態與一次性建模2種計算方法的對比研究主要有2類。第1類研究直接利用有限元分析軟件，對2種計算方法得到的分析結果進行對比，然而并未分析產生上述差異的根本原因[5-6]；第2類研究基于非線性有限元基本原理，通過對有限元方程中剛度矩陣、荷載列陣、位移列陣及邊界條件的非線性變換推導出考慮施工狀態與一次性建模2種計算方法的差異[7-9]。然而基于非線性有限元的推導過程對力學功底要求較高，一般的技術人員較難理解，在工程實際應用中接受度不高，難以推廣。

本文從高層建筑豎向壓縮變形的角度入手，研究考慮施工狀態與一次性建模2種計算方法產生差異的基本原理。將高層建筑簡化為一單桿，采用材料力學基本原理推導其在自重作用下考慮施工狀態與否的豎向壓縮變形函數，從而得到一次性加載及考慮施工狀態的豎向壓縮變形曲線。簡單而直觀地反映了一次性加載及考慮施工狀態的豎向壓縮變形的基本原理。

1 考慮施工狀態的壓縮變形函數

本節以圖2所示的單桿為例，對考慮施工狀態的壓縮變形函數進行推導。該單桿長度為l，截面積為A，重度為r，彈性模量為E，第i個微段的自重為Gi。

圖2 考慮施工狀態單桿計算簡圖

假設結構在第n施工步的完工面標高為x，由于施工時各樓層標高均會找平，故第n施工步的完工面標高x與設計標高一致。設在第n＋1施工步，x標高以上新完工結構自重為Gi＋1，則第n＋1施工步，x標高處新產生豎向位移為：

因此，結構施工到頂后，x標高處合計產生的豎向位移為：

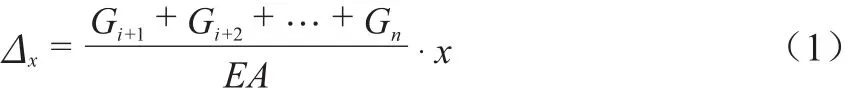
由公式（1）可知，考慮施工狀態時，結構完工后高度x處產生的豎向壓縮變形值等于高度x以上結構自重對高度為x的部分產生的壓縮變形，即：

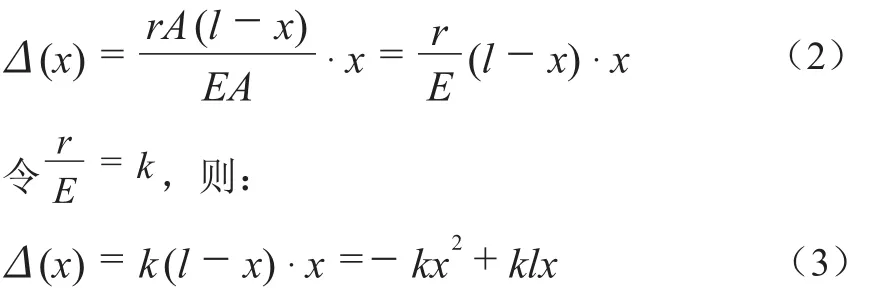
由公式（3）可知，僅計入自重時，考慮施工狀態的壓縮變形函數為二次函數（圖3），壓縮變形最大值位于桿件高度l/2處，桿件底部及桿件頂部的壓縮變形值為0。

圖3 考慮施工狀態的單桿壓縮變形曲線

2 一次性加載的壓縮變形函數

本節以圖4所示的單桿為例，對一次性加載的壓縮變形函數進行推導。該單桿長度為l，截面積為A，重度為r。

圖4 一次性加載單桿計算簡圖

在距離桿底x高處取出長度為dx的微段，略去該微段自重對變形的影響，則該微段的變形為：

對0到x高度范圍的微段變形進行積分，得到一次性加載后高度x處產生的豎向壓縮變形[10]，即：

由公式（6）可知，僅計入自重時，一次性加載的壓縮變形函數為二次函數（圖5），壓縮變形最大值位于桿件高度l處，桿件底部壓縮變形值為0。

圖5 一次性加載的單桿壓縮變形曲線

3 算例

一高度為202 m的框架核心筒結構，共55層，利用有限元分析軟件MIDAS GEN建立結構模型（圖6）。

該塔樓采用核心筒與外框架同步上升的施工方法。在MIDAS模型中，將每3層定義為一個施工步，不考慮混凝土的收縮徐變特性，經施工模擬分析與一次性加載分析，得到核心筒與外框架柱的壓縮變形曲線，位移提取點的平面位置分別位于核心筒與框架柱的4個角點處（圖7）。

核心筒豎向變形取其4個角點豎向變形的平均值，將一次性加載、施工過程模擬的計算結果進行統計（圖8）。

框架柱豎向變形取其4個角點豎向變形的平均值，將一次性加載、施工過程模擬的計算結果進行統計（圖9）。

圖6 結構模型

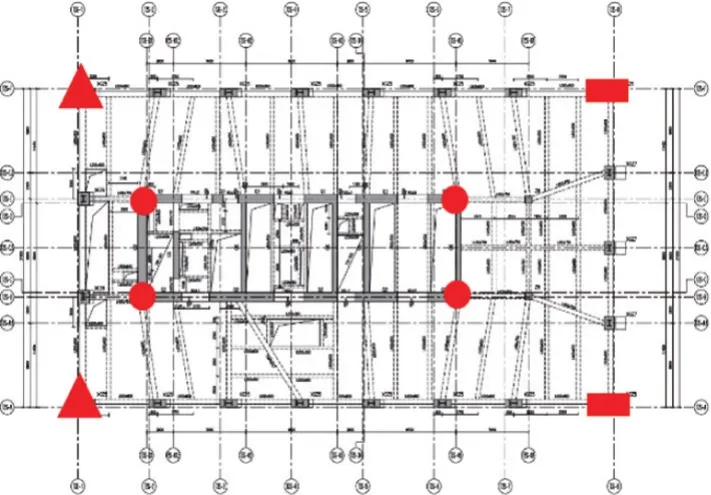
圖7 位移提取點示意

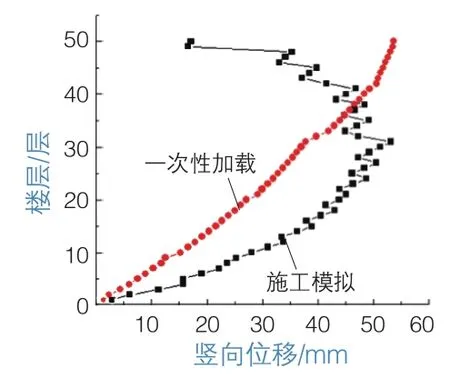
圖8 核心筒豎向變形計算結果

圖9 框架柱豎向變形計算結果

由上述分析結果可知，考慮施工狀態時，核心筒與外框架的豎向壓縮變形曲線大致呈二次函數曲線的形狀，最大值在結構中上部；在一次性加載的情況下，核心筒與外框架的豎向壓縮變形曲線最大值位于結構頂部。上述豎向壓縮變形曲線的整體趨勢與本文推導的公式（3）、公式（6）相符。由于實際結構豎向剛度分布不均，以及受混凝土收縮、徐變等時間相關因素的影響，故實際結構的豎向壓縮變形曲線不嚴格遵循二次函數，在考慮施工狀態的情況下，豎向壓縮變形最大值不位于結構中部，而是位于結構中上部。

4 結語

本文利用材料力學的基本原理，通過將高層建筑簡化為一單桿，推導了高層建筑一次性加載及考慮施工狀態的豎向壓縮變形函數，得到如下結論：

1）考慮施工狀態的高層建筑豎向壓縮變形函數為公式（3）。由公式（3）可知，考慮施工狀態時，結構豎向壓縮變形曲線為二次函數曲線，結構底部與頂部壓縮變形最小，中部壓縮變形最大。

2）一次性加載的高層建筑豎向壓縮變形函數為公式（6）。由公式（6）可知，一次性加載時，結構豎向壓縮變形曲線也為二次函數曲線，結構底部壓縮變形最小，結構頂部壓縮變形最大。

3）利用通用有限元軟件MIDAS GEN，對一實際工程項目進行考慮施工狀態及一次性加載下的豎向壓縮變形分析。分析結果表明，實際工程項目的豎向壓縮變形曲線與本文推導得到的簡化函數曲線基本一致。但由于實際結構存在豎向剛度分布不均，以及受混凝土收縮、徐變等時間相關因素的影響，故其豎向壓縮變形曲線不嚴格遵循二次函數。

本文從根本上揭示了高層建筑一次性加載及考慮施工狀態的豎向壓縮變形的力學原理，簡化了以往采用非線性有限元方法的推導過程，更加便于普通工程技術人員理解、掌握，有利于高層建筑施工過程模擬的推廣應用。

此外，本文推導得到的簡化計算公式可作為高層建筑豎向壓縮變形的手算工具，用來檢驗軟件計算結果的合理性。