自適應多層復形遺傳算法在鈦合金動態本構模型參數識別中的應用

盛 鷹， 曾祥國， 陳國平， 劉筱玲， 文 軍

(1.西南科技大學 土木工程與建筑學院， 四川 綿陽 621000； 2.四川大學 建筑與環境學院， 四川 成都 610065)

0 引 言

鈦合金因具有密度小、比強度高、耐高低溫、耐腐蝕等綜合性能，而被廣泛運用于航空航天、生物醫療等領域[1-2].與其他金屬材料不同的是，鈦合金材料對應變率和溫度非常敏度，在高應變率、高溫環境下表現出與中應變率、常溫環境下截然不同的力學性能[3].為準確描述鈦合金材料與不同應變率、不同溫度相關的力學行為，學者們提出了多種本構模型，如Johnson-Cook模型、Khan-Huang-Liang模型、Chaboche模型等[4-6].其中，Johnson-Cook模型是一種常用的經驗型本構模型，其形式簡單，各參數具有清晰、明確的宏觀物理含義，參數個數較少，能較好地模擬多種常用工程材料的動態本構行為，能廣泛用于工程結構或重要構件在動態載荷作用下的動力學模擬分析.此外，針對鈦合金在高應變率下表現出的熱粘塑性，學者們驗證了Johnson-Cook模型能很好地擬合鈦合金在低應變率和中應變率下的動態拉壓行為，但卻不能方便地描述其在高應變率下的應力—應變關系[7-8].為使Johnson-Cook模型能廣泛適用于描述鈦合金在不同應變率、不同溫度下的應力—應變關系，本研究在Johnson-Cook模型基本形式不變的情況下，重新定義了溫度項的物理意義和表達形式，得到了修正的廣義Johnson-Cook模型，可很好地解決了這一問題.但廣義Johnson-Cook模型中含有6個需要通過大量實驗數據來擬合確定的待定參數.為降低參數識別的計算工作量，提高參數識別的效率和精度，本研究在遺傳算法[9]和復形法[10]的基礎上，提出了一種自適應多層復形遺傳算法，其能顯著提高參數識別的效率和精度，并以Ti-6Al-4V鈦合金為算例，描述了其在不同應變率、溫度下的單軸流變應力—塑性應變曲線，數值模擬結果和已有的試驗數據吻合良好.

1 鈦合金Johnson-Cook動態本構模型

1.1 經典Johnson-Cook模型

經典Johnson-Cook模型是一種常用的經驗型本構模型，其流變應力—塑性應變關系表達式為，

(1)

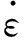
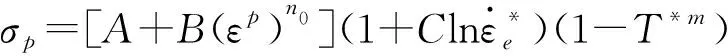
(2)

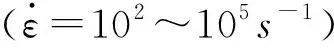
1.2 Johnson-Cook模型溫度項修正

(3)

式中，β為功熱轉換系數，ρ和Cp為材料密度和比熱容，k為常系數.

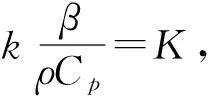
Tt+1=Tt+(ΔT)t+1

(4)

因此，在經典Johnson-Cook模型的基礎上，將溫度項T修正為材料的瞬時實際溫度，即考慮T為與時間t相關的量，則只需用式(4)的Tt+1代替式(1)的T，即可得到修正的廣義Johnson-Cook模型，

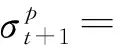
(5)

需要說明的是，在低應變率和中應變率下，多數金屬材料的內部溫度來不及升高就已經擴散，此時K≈0,修正廣義Johnson-Cook模型就退化為了經典Johnson-Cook模型.因此，經典Johnson-Cook模型其實是該修正廣義Johnson-Cook模型的一種特殊情況.

2 自適應多層復形遺傳算法

2.1 多參數識別數學模型

本構參數識別的目的是尋找一組材料參數，使計算值與試驗值之間的綜合誤差最小，如式(6)所示，

(6)

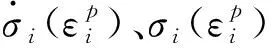
對此，本研究將采用自適應多層復形遺傳算法進行本構參數識別，使目標函數(6)取到最小值.

2.2 自適應多層復形遺傳算法

自適應多層復形遺傳算法的基本步驟包括：形成初始復形，檢驗收斂條件，找到最壞點，調優搜索尋求改進點.如此反復進行，使復形逐漸縮小，逼近最優點，然后在最優點附近用遺傳算法作局域精確搜索.其具體實現步驟如下：

1)采用隨機試驗法投點，形成初始復形.

首先對可能的范圍作上、下界估計，以確定試驗域和采用隨機試驗法投點.此處可能的初始投點范圍不必包含各參數的最優解.

為了能有效控制隨機數精度，采用random(num)函數產生1到num之間的隨機整數，再取倒數則得到了0到1之間的隨機數ζ.于是，各頂點的變量列陣可表達為，

(7)

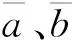
改進技巧包括：其一，首先產生一組隨機數存放于數據文件中備用，為避免產生偽隨機數，要通過比較和篩選確保產生的隨機數不出現重復；其二，若產生的某個初始點不滿足約束條件，則順次讀入下一個隨機數構成新的初始點再進行判斷，直到所有頂點全部可用為止.

2)對復形各頂點的目標函數值進行排序，檢驗收斂條件.

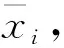
處理技巧為：第一層復形均以迭代次數作為停機準則，各個復形分別迭代5到10次則停止.但第二層復形則以式(8)作為終止迭代依據.若成立則終止迭代，反之進入“調優搜索"步進行再次迭代.

(8)

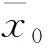
(9)

通過這種改進，一方面有效減少了結構分析次數，另一方面也找到了停止迭代的合理判據，確保終止迭代后的最好點接近全局最優點.當第一層復形迭代完成后，則初始化第二層復形.這里有一個改進技巧：傳統的多層復形法僅從各復形中取出最好與次好點組成第二層復形，但如果各復形頂點較多，則選點個數不僅僅局限于最好與次好點.適當增加選點個數可有效減少優化分析次數，而不會對精度造成影響.

3)調優搜索階段.

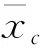
(10)

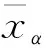
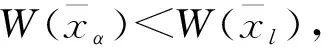
(11)

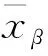
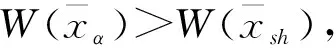
(12)

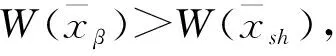
完成調優搜索過程后，則返回第3)步再次對新復形各頂點對應的目標函數排序和檢驗收斂條件.直到滿足收斂條件(8)時，復形迭代終止.

其中，第3)步的調優搜索子程序流程圖如圖1所示.第1)～3)步程序設計流程圖如圖2所示.

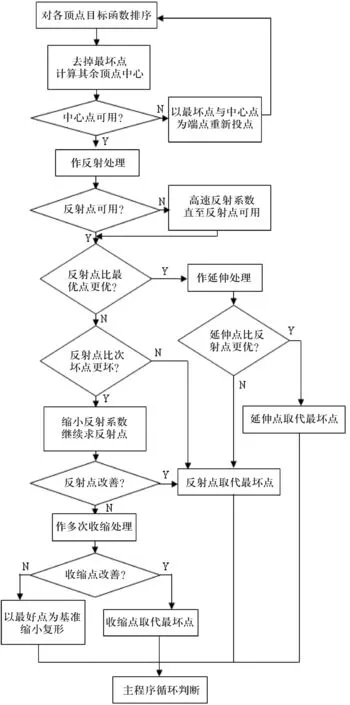
圖1 第3)步調優搜索子程序流程圖

4)在最優點附近用遺傳算法作局域精確搜索.

(13)

式中，γi為變量xi附近的搜索鄰域.

然后對各變量在調整后的范圍內，運用遺傳算法[14]進行更精密的智能進化搜索，通過選擇、交叉和變異運算，可獲得精度更高的最優解.

第4)步遺傳算法局域精確搜索的子程序流程圖如圖3所示.

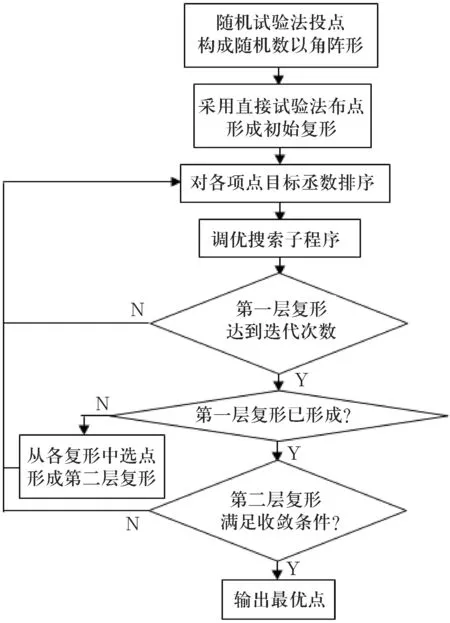
圖2第1)～3)步程序流程圖

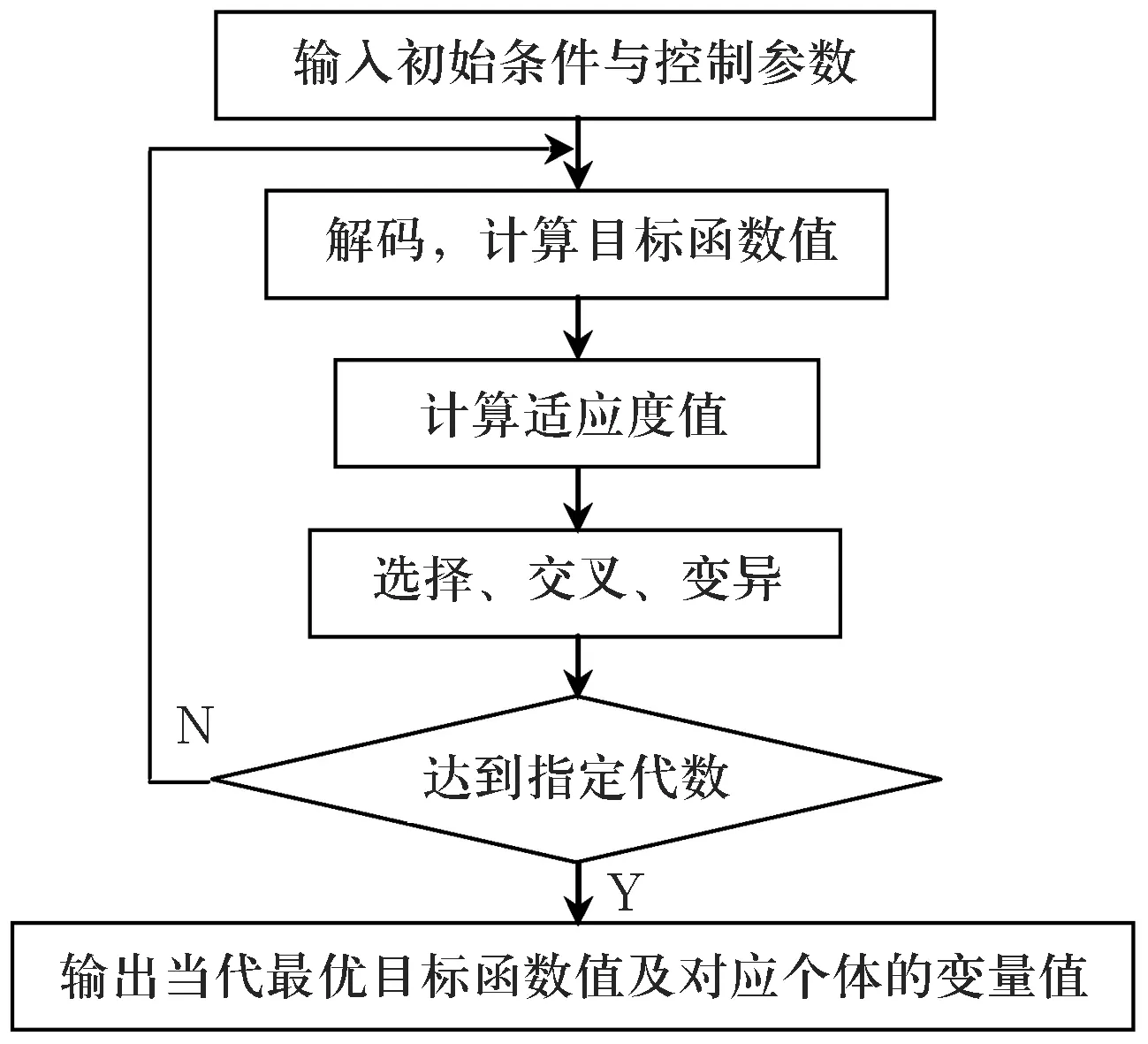
圖3 第4)步遺傳算法搜索子程序流程圖

3 算例分析

本研究以Ti-6Al-4V鈦合金(熔點溫度Tm=1 933 K，彈性模量E=107 800 MPa)為例，采用準靜態試驗和動態加載試驗獲得的多種應變率、溫度下的流變應力—塑性應變試驗數據[7]，對本研究建立的修正的廣義Johnson-Cook模型及待定參數的識別方法進行驗證.

修正的廣義Johnson-Cook模型中Ti-6Al-4V鈦合金的各材料常數如表1所示.

表1 修正的廣義Johnson-Cook模型中Ti-6Al-4V材料常數

將表1所得的各參數值代入式(5)的本構模型中即可得到不同應變率、不同溫度下鈦合金的流變應力—塑性應變關系.在不同低應變率、不同溫度下， Ti-6Al-4V鈦合金的流變應力—塑性應變的試驗數據和計算結果比較如圖4所示；在不同高應變率、不同溫度下，Ti-6Al-4V鈦合金的流變應力—塑性應變的試驗數據和計算結果比較如圖5所示.

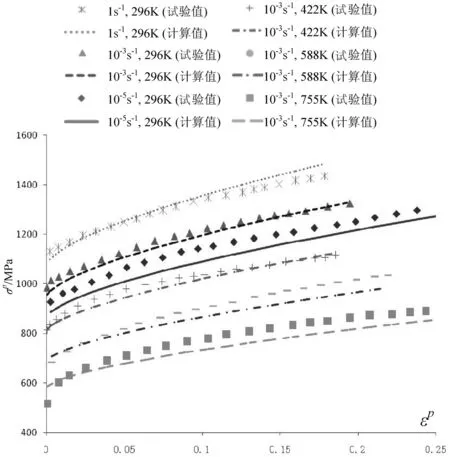
圖4不同低應變率、不同溫度下Ti-6al-4V的應力—應變曲線的試驗和計算比較

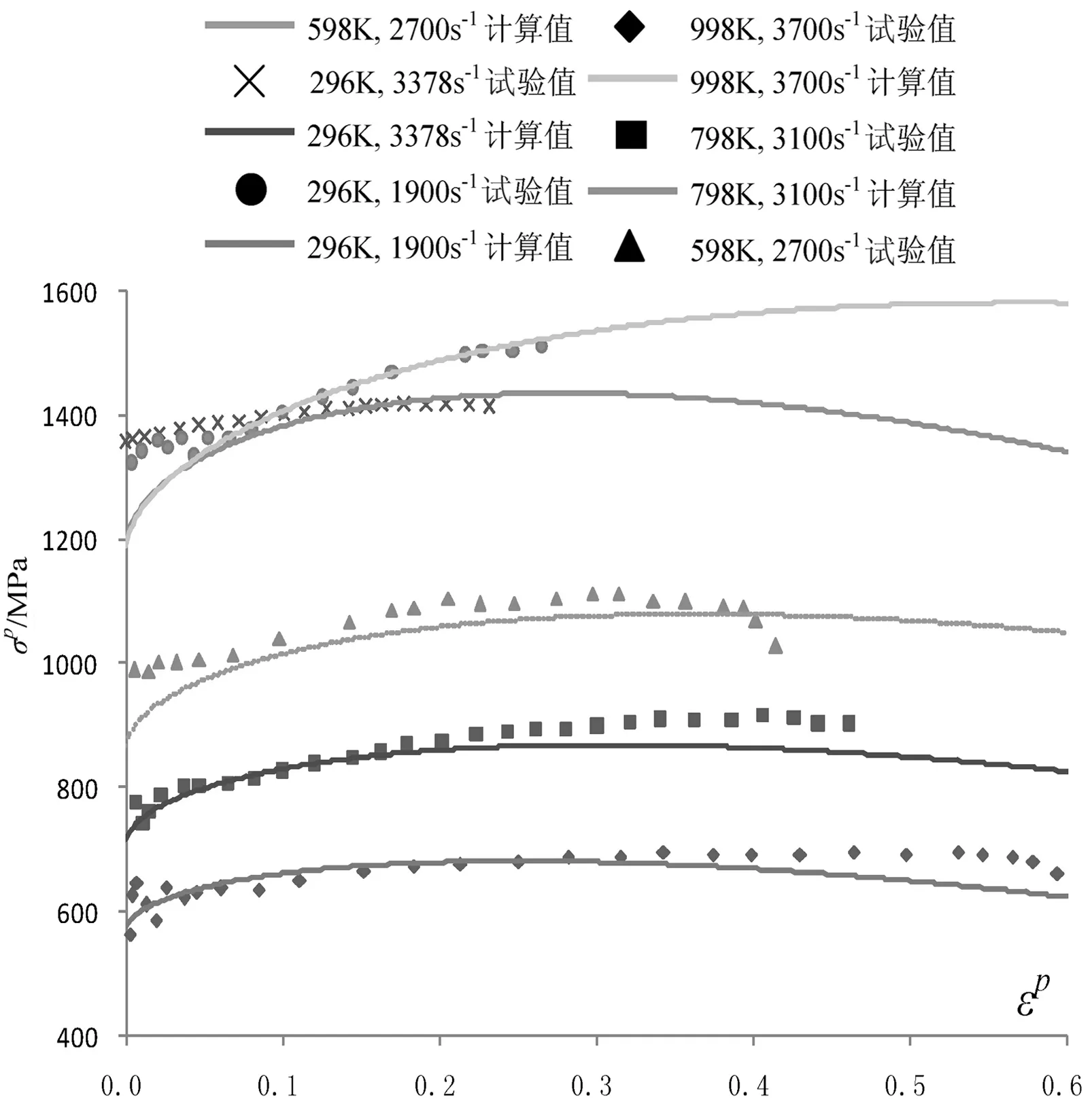
圖5 不同高應變率、不同溫度下Ti-6al-4V的應力—應變曲線的試驗和計算比較

由圖4和圖5可知，計算結果與試驗數據吻合良好.此驗證了本文提出的修正廣義Johnson-Cook模型與自適應多層復形遺傳算法的可靠性.

需說明的是，表1中擬合得到的6個Ti-6Al-4V材料常數是運用圖5中5組不同的高應變率、不同溫度下的試驗數據獲得的，再將求出的待定參數代入修正廣義Johnson-Cook模型中，進而可獲得6組不同低應變率、不同溫度下的擬合曲線.由圖4可知，這些擬合曲線與不同低應變率、不同溫度下的試驗值吻合仍較好.此表明該修正廣義Johnson-Cook模型對Ti-6Al-4V材料的本構關系具有較好的預測性.

4 結 論

鈦合金是應變率敏感材料，在中應變率及以下的加載條件下，在相同的溫度下，應變率越高，給定應變下的流變應力也越高.在高應變率下，鈦合金表現出熱粘塑性，由于加載速度很快，鈦合金內部溫度迅速升高且來不及擴散，將降低應變、應變率的強化作用，使流變應力呈下降趨勢.本研究提出的修正的廣義Johnson-Cook模型能較好地擬合鈦合金在不同應變率(低應變率、中應變率、高應變率)、不同溫度(常溫、高溫)下的本構關系.本研究提出的自適應多層復形遺傳算法有效克服了復形法、遺傳算法存在的無法同時滿足精度、可靠性和計算時間3方面的要求，且方法無需預先估計各待定參數最優解所在的取值范圍，顯著提高了對最優解的全局搜索能力，能快速、精確、可靠地實現優化問題的求解.此外，本研究提出的確定材料本構關系材料常數的自適應多層復形遺傳算法對其他工程材料高精度本構關系的建立具有重要參考價值.