多模態化工過程動態多點故障監測方法

胡瑾秋， 羅 靜， 郭 放

(中國石油大學(北京) 油氣資源與工程國家重點實驗室 機械與儲運工程學院， 北京 102249)

實際生產中，多模態化工過程除了可能存在非高斯特性以外，還會受到環境和操作干擾，產生噪聲。當生產過程處于不同生產模態時，正常的過程數據的均值、方差和相關關系等特征變量會出現較大的波動。目前，在多模態化工過程監測領域應用最多的是多元統計過程故障監測技術[1]。多元統計方法不需要根據過程機理建立復雜模型，并且可以降低數據維度。近年來，國內外學者也開展了相應的研究，主要分為以下兩類：基于主元分析方法的技術和基于獨立成分分析方法的技術。大多針對多模態化工過程的特點采取主元分析與其他方法相結合的手段對過程進行監控。盧春紅等[2]采用主元分析結合核函數的方法處理高斯數據的非線性問題，從概率角度刻畫數據集的多個局部分量特征，在提取的核主元分量內獲得測試樣本的后驗概率，結合貝葉斯推理進行故障檢測。Zhang等[3]采用遞歸核主元分析法應用于連續退火工藝的動態過程監測，能夠有效地監測出過程故障。部分學者用主元分析結合聚類算法和奇異值識別算法來解決過程的多模態問題[4-8]。基于獨立成分分析方法的技術，主要處理過程的非高斯問題，也與其他方法結合處理多模態過程中的其他問題。趙小強等[9]采用獨立成分分析(Independent component analysis, ICA)結合核函數解決非高斯數據的非線性問題，進行化工過程的故障檢測。還有一些將ICA[10]結合聚類算法、奇異值算法和其他方法解決過程的多模態問題[11-15]。

然而，雖然已有的多元統計監測方法解決了多模態化工過程的非高斯性，但是這些方法均采用靜態控制限對統計量進行監測，魯棒性差，會因噪聲產生誤報。因此，針對上述問題，筆者提出多模態化工過程動態多點故障監測方法。基于粒子群優化的ICA算法和自回歸(Autoregressive, AR)模型構造不同平穩過程的非高斯監測模型，計算平穩過程的單點監測統計量和多點異常統計量。基于粒子群優化的ICA算法構造過渡過程的非高斯監測模型。平穩過程和過渡過程均采用動態控制限實施監控。案例分析中，分別將傳統的統計量控制限求解方法3σ法與動態多點監測方法應用到丙烯計量罐裝置進行對比。

1 動態多點故障監測方法基本理論

1.1 AR模型

為了解決多模態化工過程監測數據的非高斯性和高維度，引入粒子群優化的ICA算法來計算不同過程模態的非高斯統計量，基于非高斯統計量建立平穩過程AR監測模型。AR模型要求時間序列{Xt}趨勢平穩、均值為0。AR模型是p階自回歸模型，記為AR(p)，其中p是模型的階數，N是時間窗寬，如公式(1)所示。

Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p+εt

(1)

式中：φ1,φ2,…,φp是AR(p)的自回歸系數，εt是均值為0、方差為σ2的獨立同分布高斯隨機白噪聲。AR模型的階數p與窗口N滿足約束條件：

0≤p≤0.1N

(2)

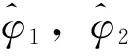
(3)

(4)

(5)

1.2 單點監測統計量

參考網絡流量異常定義準則，用觀測值與AR模型預測值的殘差來定義化工過程異常，而過程的最終監測統計量則采用單點監測統計量和多點異常統計量。

(1)殘差e

定義零均值化后的觀測值序列為{…,x(t+1),x(t+2),x(t+3),…}，由AR模型擬合所得的預測值序列為{…,y(t+1),y(t+2),y(t+3),…}，那么，殘差序列{…,e(t+1),e(t+2),e(t+3),…}按照下式計算：

e(t+i)=x(t+i)-y(t+i)

(6)

(2)單點監測統計量W

(7)

其中，ξ2=(e2(t+1)+e2(t+2)+…+e2(t+N+1))/(N+1)。通過單點監測統計量W(t+N+1)判斷預測值y(t+N+1)是否正常，當W(t+N+1)>U(t+N+1)時，y(t+N+1)是異常的，否則，y(t+N+1)是正常的。U(t+N+1)代表單點監測統計量W(t+N+1)在t+N+1時刻的控制限，數值由下式計算：

U(t+N+1)=μ+k×σ

(8)

其中，μ和σ分別是正常歷史觀測值對應的殘差正序列的均值和標準差，k取值為2或3，初值為2。若前一時刻的預測值y(t+N)被判斷為正常狀態，則令當前時刻k=2。當y(t+N)指示異常時，為了減少過程干擾產生的誤判，此時令k=3，即適當降低檢測點的監測標準。

1.3 多點異常統計量

多模態化工過程由于其自身的復雜特性和員工的頻繁操作，即使處于正常狀態，過程檢測點數值也有可能具有短暫的較大波動。化工過程異常時，不會只有某個孤立的檢測點異常，勢必會引發鏈式效應。因此，為了確保有效報警率，有必要設置多點異常統計量λ，根據多個連續檢測點的異常情況來判定是否需要報警。定義λ為當前檢測點距離前一個異常檢測點的時間間隔a和一定時間內異常發生次數的函數。在一定時間內，過程發生異常的次數越多，λ值越大，過程異常程度越大。記λt為檢測點在單點時刻t的異常統計量，初值為0。在初次檢測到異常發生時，根據單點監測統計量超出控制限的部分計算λt和λ，如式(9)和式(10)所示：

λt=W(t+N+1)-U(t+N+1),

W(t+N+1)>U(t+N+1)

(9)

(10)

當多點異常統計量λ超過其控制限Uλ，說明在當前時間窗口中有多個連續的檢測點發生異常，報告異常發生。λ的控制限Uλ為發生異常的點數n與k=3時的單點監測統計量控制限的積，計算如下式：

Uλ=n×(μ+3σ)

(11)

為避免誤報警，需進一步計算多點異常統計量λ來判斷異常。增大k值，減小λt，放緩多點異常統計量λ的增長。如果有2個以上連續相鄰的點的單點異常統計量λt超過閾值，會造成多點異常統計量λ以2倍指數的形式呈現爆炸式增長，并迅速越過報警限。如果沒有連續異常點出現，單點監測統計量W(t+N+1)必須遠遠超出閾值，λ才會越過控制限。若單點異常統計量λt不大，且相鄰的點沒有檢測到異常，則多點異常統計量λ會隨著時間的推移逐漸遞減為0。

2 動態多點故障監測方法

針對目前多元統計監測方法中所采用的統計量靜態控制限、魯棒性差、易因噪聲產生誤報的問題，提出多模態化工過程動態多點故障監測方法。基于自回歸(Autoregressive, AR)模型和粒子群優化的ICA算法，構造平穩模態的單點監測統計量和多點異常統計量，建立起平穩模態的非高斯監測模型。基于粒子群優化的ICA算法構造過渡模態的非高斯監測模型，平穩模態監測模型和過渡模態監測模型均采用動態監控策略，實現在線故障監測。以Hotelling’s T2統計量為例展示動態多點故障監測方法的具體步驟，平方預測誤差(Squared Prediction Error, SPE)統計量同樣適用于該方法。

2.1 離線建模

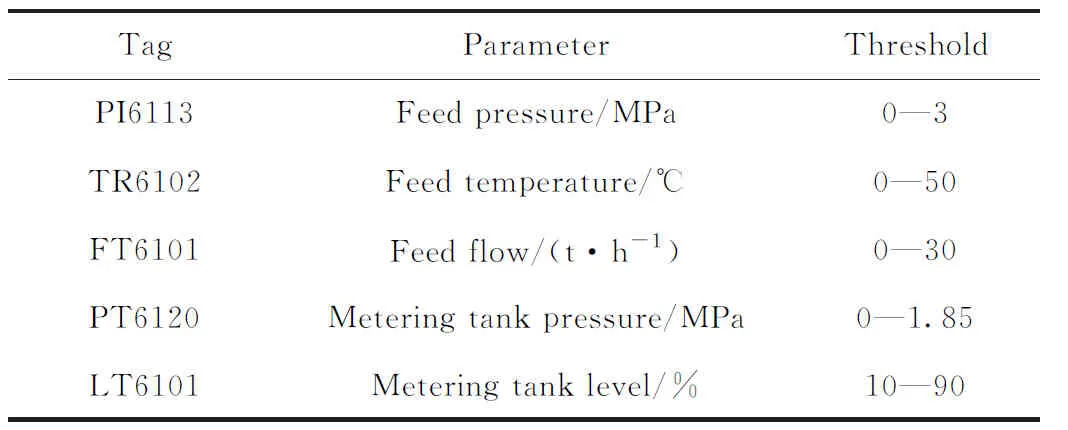
步驟1：挑選模型訓練數據。對多模態化工過程變量的正常歷史數據做Lilliefors test正態性檢驗，由檢驗標準挑出n個非高斯變量，如表1所示。取這n個非高斯變量的M個時刻的正常歷史數據作為訓練樣本X∈Rn×M；

表1 正態分布檢驗標準Table 1 Normal inspection standards

步驟2：模態劃分。用模糊C均值(Fuzzy C-means, FCM)算法將訓練樣本x離線劃分為c個不同的平穩模態和c-1個過渡過程；

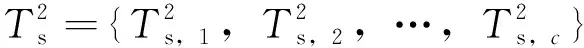
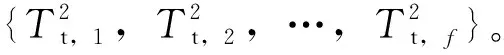
(12)

(13)

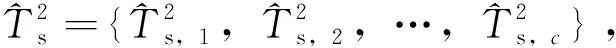
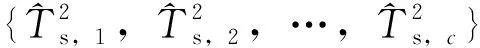
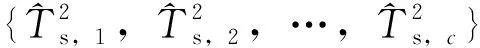
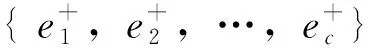
2.2 在線監測

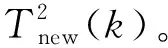
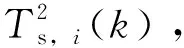
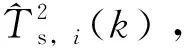
Us,i(k)=μei+d1×σei

(14)

步驟5：判斷單點監測統計量Wi(k)超限與否。若Wi(k)>Us,i(k)，d1=3，則繼續步驟8；否則，d1=2，λi(k)=0，k=k+1，返回步驟1。

步驟6：根據式(9)和(10)計算當前時刻的多點異常統計量λi(k)，并剔除當前觀測值。

步驟7：根據式(11)計算當前時刻多點異常統計量控制限Uλ,i(k)。

步驟8：判斷多點異常統計量λi(k)超限與否。若λi(k)>Uλ,i(k)，則報告異常發生，ni=ni+1；否則，k=k+1，返回步驟1。

步驟9：根據式(15)計算當前時刻過渡過程統計量控制限Ut(k)

Ut(k)=μt(k)+d2×σt(k)

(15)

2.3 方法流程圖

圖1為動態多點故障監測方法步驟圖。

3 案例分析

丙烯投料計量控制系統的作用是準確計量投入聚合釜中的丙烯量，為聚合反應控制提供前提，如圖2所示。平時丙烯經氣動三通球閥直接回丙烯中間罐循環，由可編程控制器控制氣動三通球閥進行投放料。丙烯投料計量控制系統的監控變量如表2所示。

每5 s采集1組數據，每種狀態下各采集537組數據。過程運行狀態描述：(1)正常狀態下，前1020 s，進料壓力PI6113控制在1.7 MPa以內，進料流量FT6101控制在0.01 t/h，其他變量保持穩定，過程處于平穩狀態。在第1025 s到1760 s，調小進料流量FT6101，使其他變量發生變化，過程處于過渡狀態。在1765 s以后，進料流量FT6101控制在(10.65±0.35) t/h，過程再次處于平穩狀態。(2)故障狀態下，前1270 s與正常狀態同樣的操作條件，第1275 s至第1430 s，進料閥門開度過大，進料流量FT6101大幅升高，經調節進料閥門開度，在第1495 s過程恢復正常狀態。

圖1 動態多點故障監測方法步驟Fig.1 Dynamic multi-point fault monitoring method steps

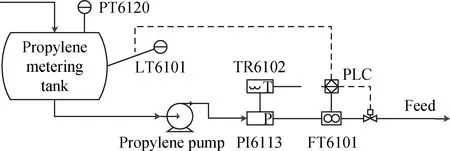
圖2 丙烯投料計量控制點流程圖Fig.2 Propylene feed metering control point flow chart

3.1 動態多點故障監測方法

挑選正常狀態下所有監測變量的537組數據作為監測模型的訓練樣本X∈R5×537，537組故障數據作為測試樣本Test∈R5×537。用FCM算法將訓練數據劃分為2個平穩模態和1個過渡過程(如圖3所示)，并針對不同模態的訓練數據分別建立各個模態下的動態多點故障監測非高斯模型。

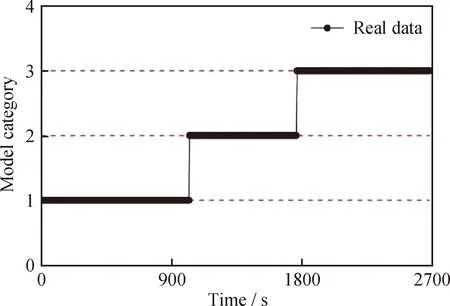
圖3 模態劃分結果Fig.3 Result of mode division

采用事先建立的故障監測模型來監測測試樣本數據，并繪制監測曲線，如圖4、圖5和圖6所示。圖4(a)為平穩模態1的Hotelling’s T2單點監測統計量監測曲線。可以看出，曲線在第765 s至第880 s間有較大波動，在個別點控制限有所提高，但在第840 s和第860 s仍有數據超過控制限，這兩點是連續異常點，初步判斷此時系統異常。圖4(b)為平穩模態1的Hotelling’s T2多點異常統計量監測曲線，只有在第840 s和第860 s，多點異常統計量有數值，但均未超過控制限。故平穩模態1的Hotelling’s T2監測結果為全過程處于正常狀態。圖4(c)是平穩模態1的SPE單點監測統計量監測曲線，可以看出，曲線隨著時刻增長隨機波動，整體上無明顯趨勢。控制限數值幾乎固定在2.7，只有在第740 s、第870 s和第970 s控制限數值稍有提高，但無數據點超過控制限，系統全過程處于正常狀態。

圖4 平穩模態1的監測結果Fig.4 Monitoring results of the stationary mode 1(a) Hotelling’s T2 single point monitoring statistic; (b) Hotelling’s T2 multiple points anomaly statistic; (c) SPE single point monitoring statistic

圖5(a)為過渡過程的Hotelling’s T2統計量監測曲線。可以看出，前1270 s曲線隨著時刻增長有下滑趨勢，在第1275 s發生階躍式增長，并越過動態控制限，系統出現異常，在第1465 s發生突降，回落至動態控制限以下，此后的過渡階段曲線趨于平穩。圖5(b)為過渡過程的SPE統計量監測曲線。可以看出，前1270 s曲線隨著時刻增長有小幅隨機波動，在第1275 s越過動態控制限，系統出現異常，在第1465 s發生突降，回落至動態控制限以下，此后的過渡階段曲線在動態控制限以下維持小幅波動。

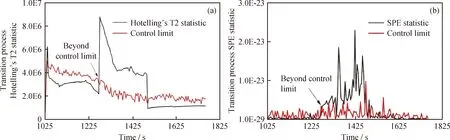
圖5 過渡模態監測結果Fig.5 Transition mode monitoring results(a) Hotelling’s T2 statistic; (b) The SPE statistic

圖6(a)為平穩模態2的Hotelling’s T2單點監測統計量監測曲線。可以看出，曲線在第1865 s至第2530 s間雖有波動，但整體趨勢較平穩。在第2535 s，統計量數值略微增長，此后維持小幅隨機波動。在第2435 s和第2655 s，曲線存在突然增長點，控制限也相應提高。除了這兩點，整個平穩模態2，控制限幾乎保持平穩，而Hotelling’s T2單點監測統計量沒有超過控制限，系統處于正常狀態。圖6(b)為平穩模態2的SPE單點監測統計量監測曲線。可以看出，曲線隨著時刻增長上下大幅波動，沒有明顯趨勢。在第2565 s至第2595 s間有個別點波動較大，控制限也相應提高。過程的所有數據點均未超過控制限，說明系統維持在正常狀態。另外，平穩模態2無連續異常點出現，故多點異常統計量始終為0。

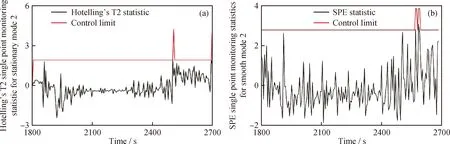
圖6 平穩模態2的監測結果Fig.6 Monitoring results of the stationary mode 2(a) Hotelling’s T2 single point monitoring statistic; (b) SPE single points monitoring statistic

3.2 基于非高斯模型的3σ法

為了驗證本文所提方法的有效性，與3σ法的監測結果對比。根據3σ法，統計量控制限為統計量均值與其3倍標準差的和。應用3σ法監測Hotelling’s T2統計量和SPE統計量，監測結果如圖7所示。

3.3 結果分析

將動態多點故障監測方法與傳統的基于非高斯模型的3σ法的誤報率和漏報率統計于表3。

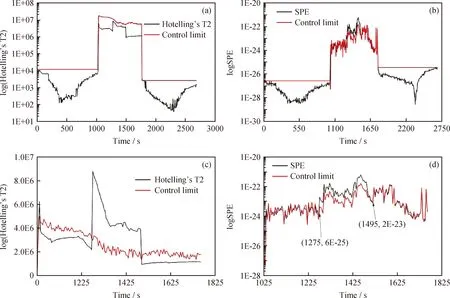
圖7 3σ法監測結果Fig.7 Monitoring results of 3σ(a) Hotelling’s T2 index of the whole process; (b) SPE index of the whole process; (c) Hotelling’s T2 index of transition process; (d) SPE index of transition process

MethodT2SPEFalse alarm rate/%False negative rate/%False alarm rate/%False negative rate/%Dynamic multi-point fault monitoring method0.190.191.120.743σmethod0.930.197.450.74

結果表明，2種方法的漏報率相同，但相比較基于非高斯模型的3σ法，動態多點故障監測方法的T2統計量和SPE統計量的誤報率分別降低了0.74百分點和6.33百分點。

4 結 論

(1) 針對傳統方法所采用的靜態控制限因不能排除噪聲的干擾而產生誤報警的問題，提出多模態化工過程動態多點故障監測方法。用粒子群優化的ICA算法計算不同過程模態的非高斯統計量，平穩過程基于自回歸模型構造非高斯統計量的單點監測統計量和多點異常統計量，采用動態控制限監測，過渡過程直接采用動態控制限對非高斯統計量進行監測。

(2) 案例分析中，將動態多點監測方法應用到丙烯計量罐裝置，離線劃分過程模態，計算不同過程模態的非高斯統計量，構造平穩過程的單點監測統計量和多點異常統計量，分別采用動態控制限進行平穩模態和過渡模態的監測。

(3) 結果表明，兩種方法的漏報率相同，但相比較基于非高斯模型的3σ法，動態多點故障監測方法的T2統計量和SPE統計量的誤報率分別降低了0.74百分點和6.33百分點。因此，新方法能夠提高多模態化工過程故障監測的準確率。

符號說明：

a———時間間隔,s；

c——模態種類；

d1、d2——系數；

e——殘差；

f——樣本批次；

M——時刻，s；

m——過渡過程異常數據個數；

N——時間窗寬度，s；

n——平穩模態異常數據個數；

p——模型階數；

t——時間，s；

U——監測統計量控制限；

W——單點監測統計量；

X——時間序列矩陣；

xt——訓練樣本；

Y——模型預測序列；

y——預測樣本；

εt——白噪聲；

φi——模型系數；

σ——標準差；

λ——多點異常統計量；

μ——均值。