敏感負荷對含新能源配網規劃的影響

趙 芳, 杜兆斌

(華南理工大學電力學院，廣東 廣州 510640)

0 引言

大規模風電、太陽能等可再生能源發電功率波動會造成電壓、頻率波動和電能質量問題[1]，其高比例入網會造成一定程度的電壓波動，增加網絡的不確定性。相同功率因數時，光伏電源的滲透率越高，引起的節點電壓波動幅值也越大，同時若注入的無功功率超過局部無功負荷的需求，也會引起潮流反向[2]。如今異步電機在發電場應用仍比較普遍，運行中會消耗電網中的無功功率，在無功容量不足的情況下，會降低整個配電系統的電壓值[3-4]。

另一方面，計算機、可調速電機、直流電機驅動、交流接觸器、可編程邏輯等設備大量投入使用，其運行狀態極易受到電壓變化的影響，往往幾個周波的電壓暫降或供電中斷都會導致設備運行異常，嚴重時導致設備故障，造成大量的損失[5-7]。考慮到電壓敏感型負荷的比重在逐漸增加，配網規劃現須更加重視其供電可靠性。這些都對電網的運行和規劃提出了新的要求。從長遠來看，現有的網架規劃方案將可能滿足不了未來負荷發展的需求。

目前，國內外針對負荷的電壓敏感性以及含分布式能源發電的配電網規劃都各有不少研究。文獻[8]對可調速驅動裝置的電壓敏感度進行了分析，并繪制了不同電壓暫降類型、電容大小的電壓耐受曲線，但未考慮敏感負荷在不確定區域的損失概率。文獻[9]用電壓耐受曲線和負荷敏感度隨機模型表征負荷對電壓凹陷的敏感特性，提出了敏感負荷電壓凹陷敏感度的隨機估計方法。文獻[10]以電壓暫降嚴重性指標為依據，提出一種基于最大熵原理的負荷電壓暫降敏感度評估方法，該方法對樣本數依賴性小，無需主觀假設，但文獻[9—10]均未考慮電壓凹陷的起始點和相角跳變等因素對負荷電壓凹陷的敏感度的影響。文獻[11—12]考慮了大量分布式電源接入，其出力的波動、間歇和隨機特性對配電網風險評估造成的影響，建立了基于配電網運行風險指標的配電網評估模型。文獻[13—15]分析了分布式電源容量對配電網的影響，以維護、投資費用最低為目標函數，建立了配電網規劃多目標模型，但是規劃中缺少對配電網風險因素的考慮。文獻[16]提出了綜合考慮配電網規劃與系統運行的優化模型，將負荷丟失成本作為評價配電網可靠性的指標，但該指標不可量化計算，評價精度有待提高。由此可見，現有配電網規劃都未考慮負荷的電壓敏感特性對配網規劃的影響，規劃模型對負荷的描述可進一步發展。

本文以變頻調速電機型負荷為代表分析電壓敏感型負荷對配電網規劃的影響。首先在仿真軟件MATLAB/SIMULINK上建模，研究變頻調速電機對電壓凹陷的耐受能力，并通過電壓敏感度曲線和負荷敏感度隨機模型確定其在電壓耐受曲線不確定區域的負荷損失概率。然后分析了配網中大量敏感負荷對安全性和經濟性的影響，論述了將敏感負荷損失引入配電網規劃模型中的必要性，最終對配電網的網架規劃模型做出了改進和案例展示。

1 敏感負荷的電壓敏感特性

應用MATLAB/SIMULINK建模對典型用電設備(如變頻調速類設備)的電壓耐受能力進行分析，得到其電壓耐受能力。為后續電壓凹陷造成負荷損失的分析和評估提供數據支持。

1.1 變頻調速電機的電壓敏感性仿真

變頻器廣泛應用于電機調速，與控制系統及異步電動機一起構成變頻電機的主要組成部分，變頻方式多采用交-直-交變換，即先把工頻交流電源通過整流器轉換成直流電源，然后通過控制系統和逆變器把直流電源轉換成頻率、電壓均可調節的交流電源[17]。電壓凹陷可能影響變頻調速器的正常運行，導致電機異常，對生產過程造成損失。建立變頻電機的MATLAB/SIMULINK仿真模型，交流調速控制方式采用直接轉矩控制方式，該系統的控制部分由PI調節器、兩相/三相坐標變換、PWM脈沖發生器等環節組成。采用的電動機為MATLAB自帶模型，仿真參數為：Rs=0.214 7 Ω，Rr=0.220 5 Ω，Ls=Lr=0.009 91H，Lm=0.064 19 H，J=0.102 kg·m2，np=2，UN=400 V，fN=50 Hz。仿真模型如圖1所示。

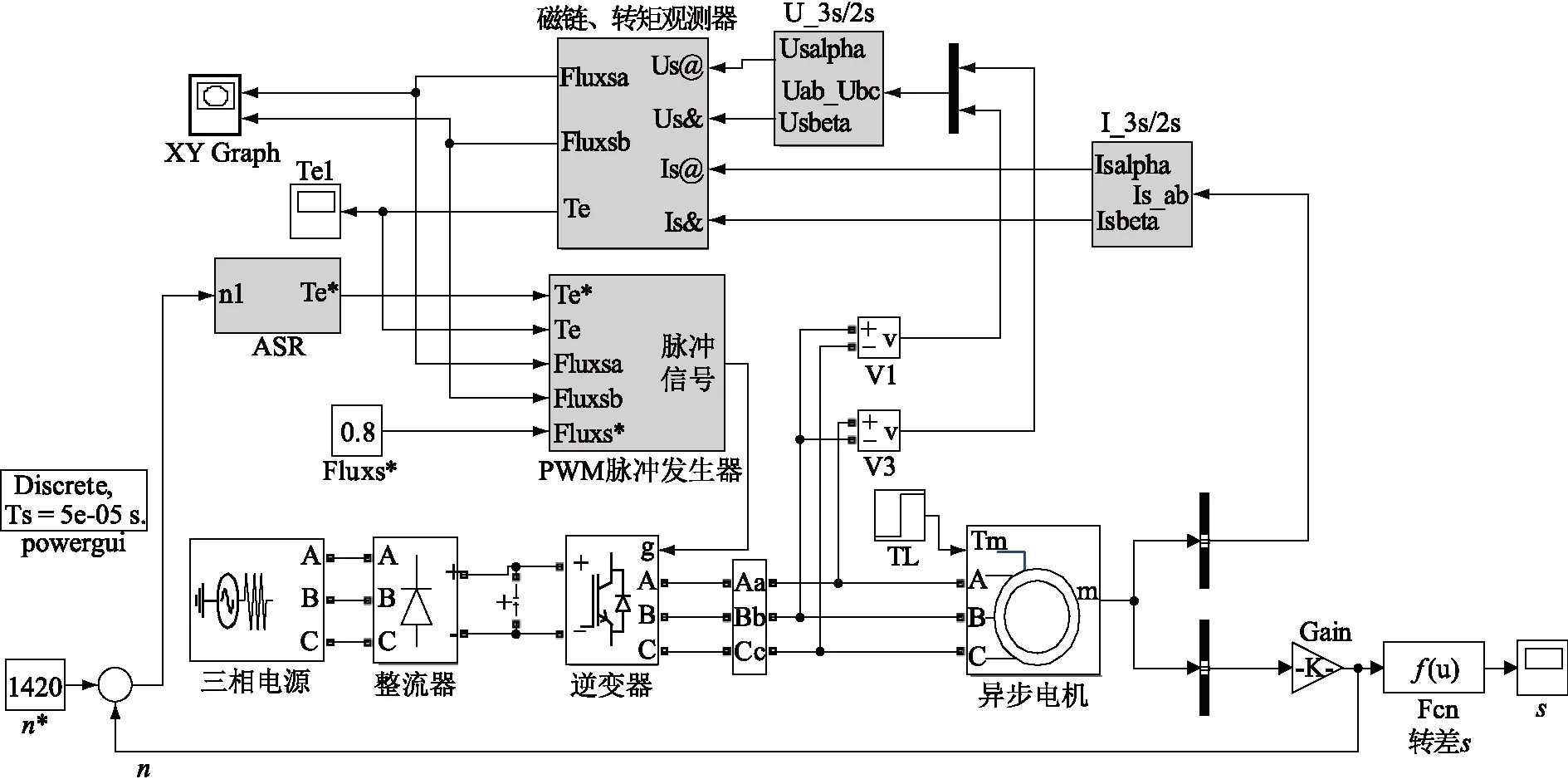
圖1 變頻電機的仿真模型Fig.1 Simulation model of frequency converter

影響變頻器的電壓暫降敏感度的主要因素有負載轉矩、電機轉速和電壓暫降類型。根據圖1的仿真模型對直接轉矩控制的三相異步電動機進行仿真研究，得到變頻電機的轉差波形，如圖2所示。仿真定轉速為1420 r/min時的空載啟動，啟動后0.1 s時加額定負載TL=100 N·m，在0.2 s時設置三相電壓暫降幅值分別為0.6 p.u.，0.7 p.u.，0.8 p.u.和0.9 p.u.，仿真時長為0.4 s。

若要求轉速不得低于1400 r/min，即轉差s不得大于0.066，該變頻電機的電壓暫降幅值和對應的臨界凹陷時間如表1所示。

1.2 部分代表性設備的電壓耐受能力

各類負荷在電網事故中對電能質量的敏感程度各有不同，通過現場調研和文獻查閱，得到幾種典型敏感負荷的電壓耐受能力:

(1) 計算機。當系統電壓降至60%，持續時間達到240 ms時，其正常運行會受到影響，導致數據丟失、重啟、關機等。

(2) 精密機械工具。電壓低于90%且持續時間超過2～3個周期，就會停止工作。

(3) 直流電機。當電壓降低到88%時，直流驅動能力將開始減弱，直流驅動的生產線將會減速，導致出現不合格產品；當電壓低于80%時，直流電機就會被跳閘，生產線會停止運轉。

(4) 變頻調速器。系統電壓低于70%并持續超過120 ms，電機自動切除。

2 電壓波動引起的敏感負荷損失

試驗表明，敏感負荷如可編程邏輯控制器(PLC)、計算機(PC)、交流調速器(ASD)的電壓耐受曲線(VTC)一般呈矩形[13]。不同的負荷類型對電壓凹陷的敏感度也有所差異，同種負荷也會受到環境溫度、安裝位置、運行時間和保養頻度等因素影響，因此負荷的電壓耐受曲線存在著不確定區域。當敏感負荷遭受該區域范圍內的電壓暫降時，負荷能否繼續正常工作并不能完全確定，而是存在一個概率。本文以這個概率作為敏感度的指標,結合電壓暫降平均水平，可評估敏感負荷受擾的經濟損失。

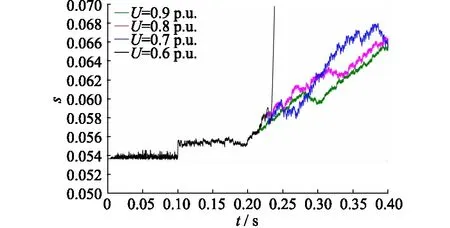
圖2 變頻電機轉差變化曲線Fig.2 Slip curve of variable frequency motor

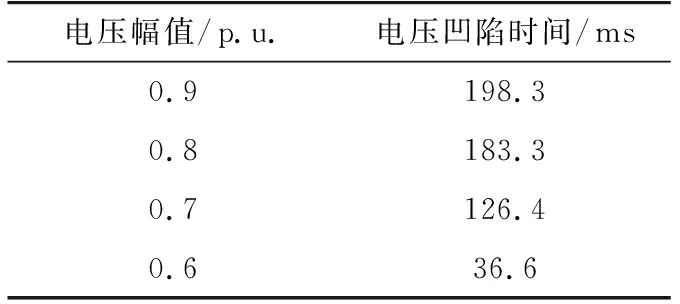
電壓幅值/p.u.電壓凹陷時間/ms0.9198.30.8183.30.7126.40.636.6

圖3中，T為電壓凹陷的持續時間；U為電壓幅值；Umin和Umax分別為實際負荷VTC的電壓幅值最小值和最大值；Tmin和Tmax分別為實際負荷VTC持續時間的最小值和最大值。曲線1的外部區域(U>Umax且TTmax為故障運行區；曲線1、2之間為不確定區域。

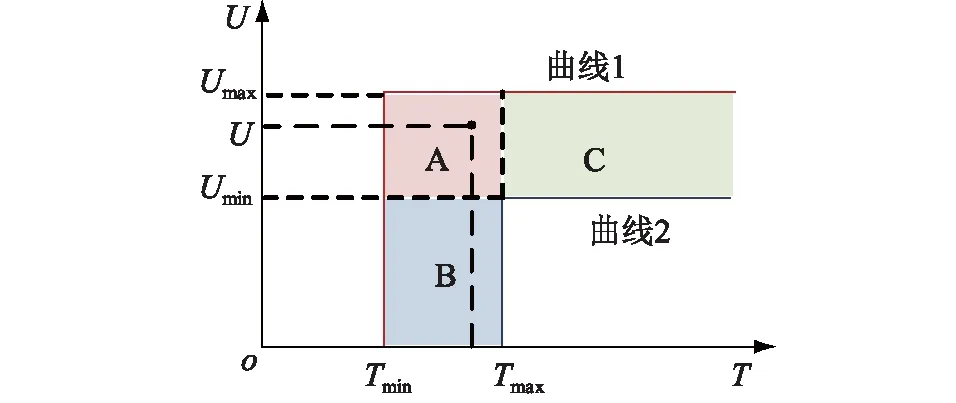
圖3 負荷電壓耐受曲線Fig.3 Load voltage tolerance curve

實際運行中負荷母線的U和T是隨機變量，用正態分布概率密度函數表征U和T的隨機性。假設B區和C區內隨機變量T和U的概率密度分別為fx(T)和fx(U)，則A區內隨機變量T和U的聯合概率密度函數及VCT 曲線的標準概率模型如下[9,18]：

fx,y(T,U)=fx(T)fy(U)

(1)

(2)

(3)

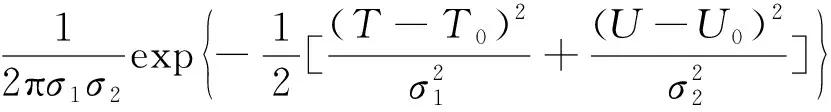
(4)

式中:σ1,σ2分別為負荷VTC在不確定區域的分布密度；T0,U0分別為VTC中T和U概率最大處的持續時間和電壓幅值。在不確定區域內，VTC 的頂點均在A區，如果已獲得母線實際電壓幅值和持續時間，則根據不同負荷的 VTC 的變化范圍可確定T0,U0，σ1,σ2，將其代入式(1—4)即可得到不確定性區域內負荷VTC的隨機估計模型。對fx,y(T,U)求定積分可求出負荷在電壓耐受曲線不確定區域范圍內的故障概率。

以變頻調速類負載為例，Umax，Umin，Tmax，Tmin在VTC中的數值分別為1 p.u.，0.7 p.u.，120 ms，0 ms。代入VCT 曲線的標準概率模型中，得到VTC在A區的概率分布，見圖4。

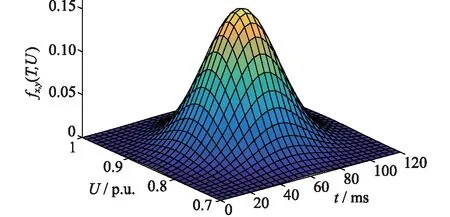
圖4 變頻調速器的VTC在A區的概率分布Fig.4 Occurrence probabilities of voltage tolerance characteristics of frequency converter in region A

對fx,y(T,U)求定積分，得到變頻調速器類負載在VTC不確定區域范圍內的故障概率如表2—4所示。

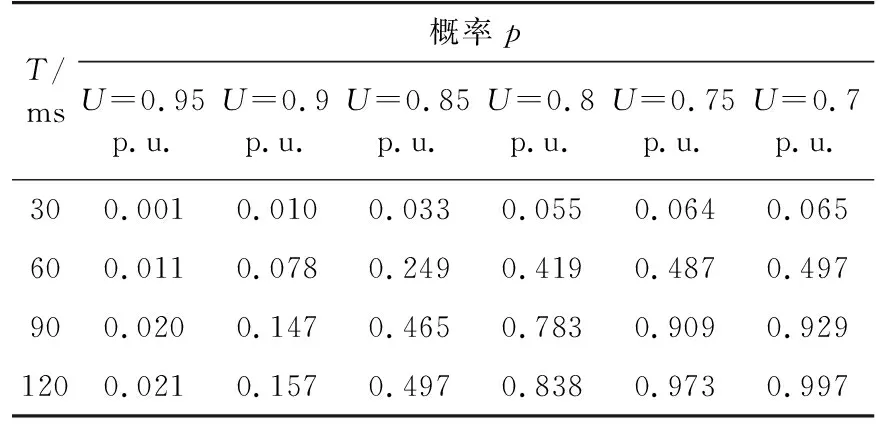
表2 變頻調速器的VTC在A區的損失概率Tab.2 Loss probability of frequency converter in region A

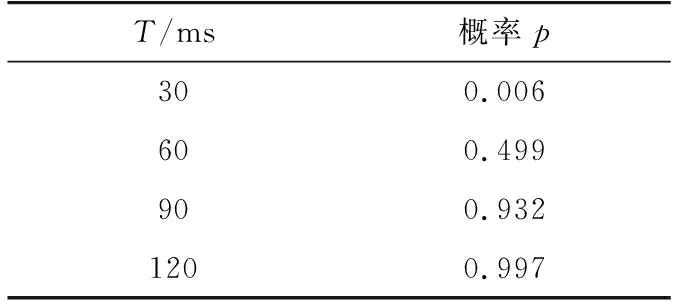
表3 變頻調速器的VTC在B區的概率分布Tab.3 Loss probability of frequency converter in region B

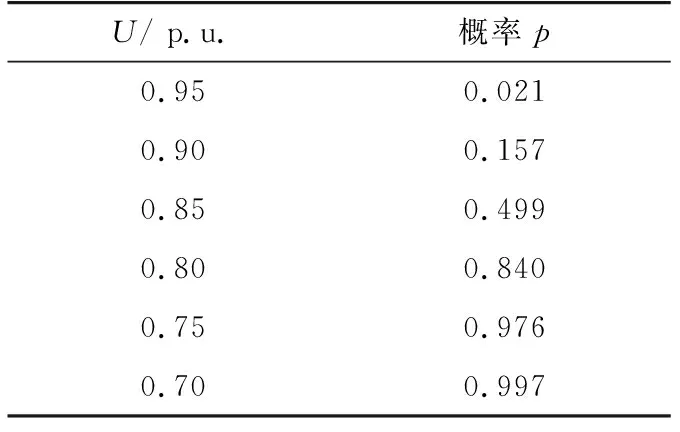
表4 變頻調速器的VTC在C區的概率分布Tab.4 Loss probability of frequency converter in region C

由表2—4可以看出，假若電壓降幅和電壓凹陷持續時間同時接近極限值時，敏感設備故障的概率極大。同樣，假若兩個變量同時接近安全值，那么故障概率將會非常小，而只有一個變量接近安全值的情況下也存在一定幾率發生故障。

3 考慮負荷損失的配網規劃模型

3.1 敏感負荷對配網的影響

電壓凹陷發生時，敏感負荷單個設備或元件的故障可能使整個生產線的產品報廢，給用戶帶來極大的經濟損失[19-20]。除此之外，大量敏感負荷還會對配網的以下幾個方面產生影響。

(1) 負荷預測。敏感負荷的產生負荷損失以及負荷恢復期間，會增大超短期負荷預測值與實際負荷值的偏差，使得用戶用能需求評估不準確。

(2) 無功規劃。對含大規模分布式電源接入的電網來說，電源接入位置和容量會影響到母線電壓水平[21]，因此敏感負荷對電壓質量的高要求會影響到無功電源的建設。

(3) 電力平衡。大量敏感負荷的突然損失及負荷恢復會造成瞬間的電力不平衡。

(4) 投資估算。負荷損失可能導致嚴重的經濟損失。此外，在響應用戶電能質量要求時，也影響到調壓穩壓設備的配置，從而導致投資成本的增加。

從以上分析可以看出，敏感負荷的電壓耐受度對電網的影響主要體現在安全性和經濟性方面，因此在未來進行網架規劃時，需要考慮敏感負荷對電壓的特殊要求。故在風險規劃的基礎上，追加考慮敏感負荷損失造成的經濟代價，對現有的網架規劃模型進行擴展和改進。

3.2 配電網規劃的數學模型

配網規劃時，在經濟性、穩定性的基礎上考慮運行風險、不同天氣狀態對網絡的影響等因素。風險因素包括切負荷和電壓越限兩個方面[3,18]，本文在此基礎上增加了電壓波動導致的負荷損失因素。根據正常和惡劣天氣條件下的線路設備故障率，采用系統切負荷期望值對切負荷量進行計算，電壓越限懲罰函數作為電壓越限評價指標。敏感負荷的損失概率和損失量的計算方法為：考慮不同天氣對發電系統輸出功率的影響，建立分布式發電系統的概率模型[22]，得出新能源在連續時間段內的輸出功率概率。依次計算潮流，得到穩態電壓分布和電壓幅值波動的影響，進而得到電壓波動曲線。在得到敏感負荷的VTC頂點后，將其代入到聯合分布密度函數(1)中，通過確定函數的積分結果，計算出電壓凹陷影響下的負荷損失概率。根據電壓波動曲線，確定各類敏感負荷的負荷損失概率，得出敏感負荷損失量及其導致的經濟損失。

3.2.1 目標函數

文中配電網風險規劃模型以待選路徑及回數作為決策變量，在保證合理風險水平的前提下，綜合考慮在規定年限內的經濟投資收益最大值。傳統風險規劃模型未考慮敏感負荷損失量，其目標函數表達式為[3]：

maxF=FPV-FL-FEC-FV

(5)

目標函數中的各分量表達式如下：

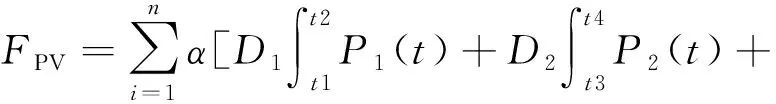
(6)

(7)

(8)

(9)

式中：F表示配電網規劃收益目標函數，求取其最大值；FPV表示配網規劃時的分布式電源總投入在一定時期內的收益；FEC表示故障線路設備引起的系統切負荷成本；FV表示電壓越限懲罰成本；FL表示配電網新增線路的投資成本；α表示平均電價；Di，Pi分別代表在不同天氣情況下的時間和發電特性曲線；CDG表示分布式發電設備建設成本；n表示分布式發電設備計劃發電年限；FL表示規劃線路造價成本；r表示貼現率；m表示規劃期限內線路設計壽命；nl表示增加線路數量；Li表示第i條線路長度；Cli表示第i條線路單位長度價格；Pk為第k種預想故障發生的概率；Ck為因第k種預想故障發生而丟失負荷量；E為所有的預想事故集；β表示單位負荷損失量的平均成本。

考慮敏感負荷損失因素，對風險規劃模型進行改進，建立目標函數：

maxF=FPV-FL-FEC-FV-Fl

(10)

Fl的表達式為：

(11)

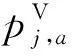
3.2.2 約束條件

(1) 功率平衡約束：

∑pij=PGi-PDi

(12)

(2) 線路潮流約束：

(13)

(3) 線路回路數目上下限約束及整數約束：

(14)

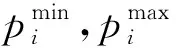
3.2.3 風險規劃流程圖

考慮天氣因素對配電網運行風險和新能源出力的影響，經過本節所述改進風險規劃評估指標進行評估，得到合理的規劃方案，改進的計算流程如圖5所示。

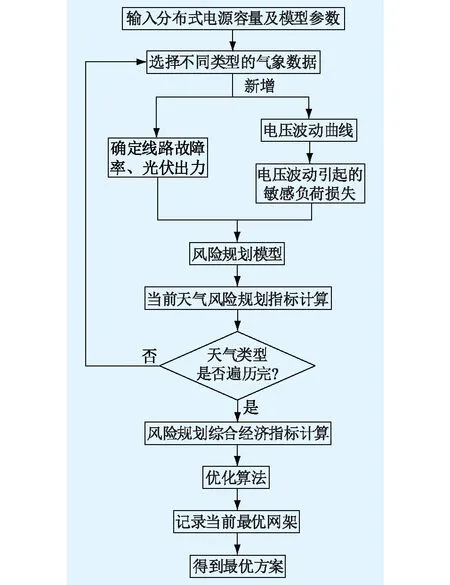
圖5 規劃流程Fig.5 Planning flow chart

4 算例

本節以配電網6節點系統為例，驗證提出的考慮敏感負荷損失配電網風險規劃方法的可行性和有效性。配網長期運行時，配網產生的電壓暫降時間都足夠長[23]，故主要考慮敏感負荷在C區的損失概率。6節點系統作為一個配電網小型測試系統，節點3為平衡節點，其余皆為PQ節點，其中節點1接有發電機，節點6上安裝了光伏裝置。具體數據見表5和表6，其中，光伏裝置投資費用11.5 元/W。

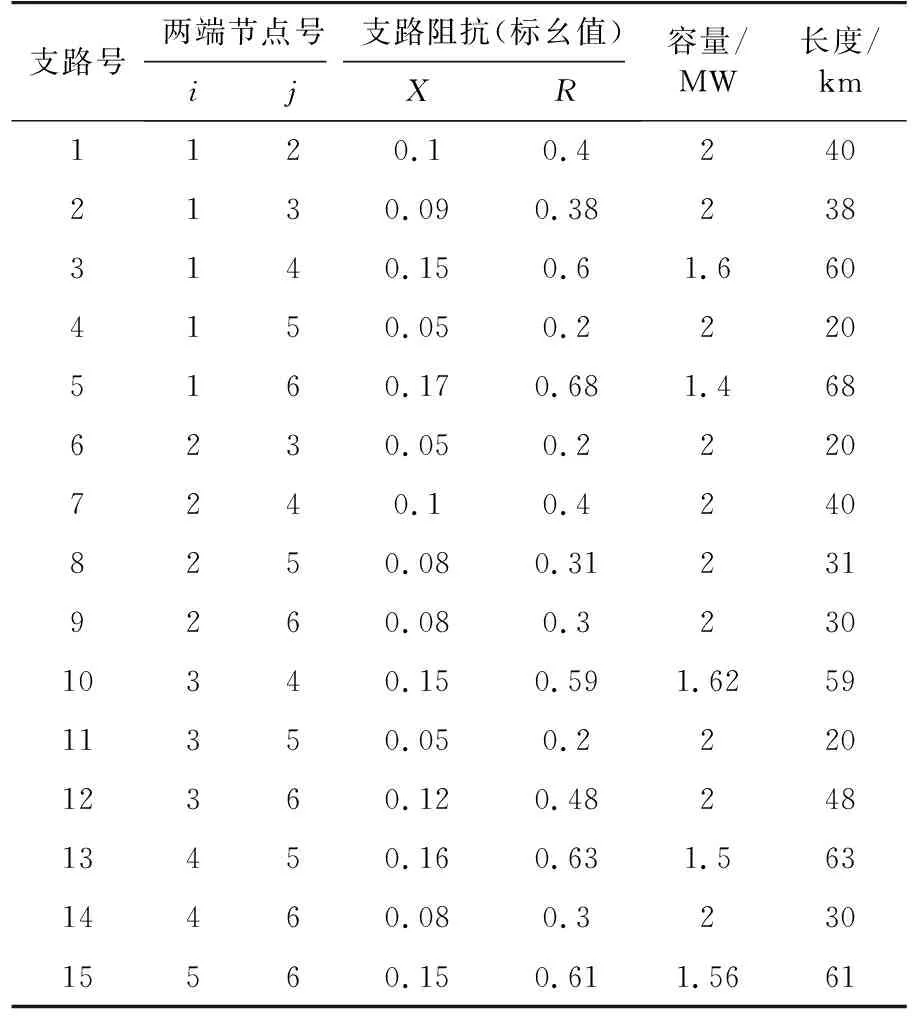
表5 支路數據Tab.5 Branch data

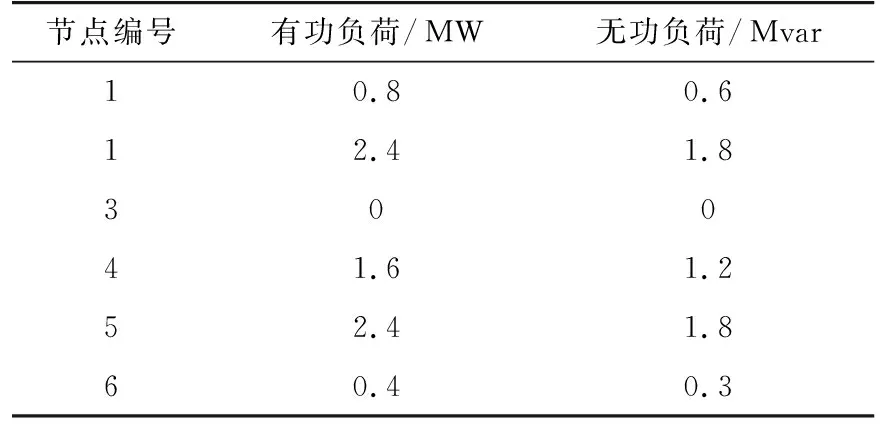
表6 節點數據Tab.6 Bus data

每度電發電收益1.15 元，規劃年限為20 a，為了分析方便，算例假設節點1,2,4,5,6存在敏感負荷，且容量均為各節點總負荷的50%，并選用我國南方某區域呈較接近正態分布的光伏出力數據，光伏滲透率約30%。

圖6中，6節點之間的15條可增線路走廊，其中實線表示現有網架，為4條單回線路。在現有網架的基礎上，每條線路走廊最多可擴建2回線路。采用粒子群算法對規劃模型進行求解，將粒子位置用支路回數的數組來表示，粒子速度用各走廊線路回數變化值矢量表示。經過500次迭代，得到不考慮敏感負荷損失時的最優網架規劃結果見圖7(a)，考慮敏感負荷損失的最優網架規劃結構見圖7(b)。

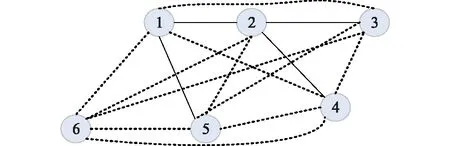
圖6 6節點網絡拓撲Fig.6 6 nodes network topology

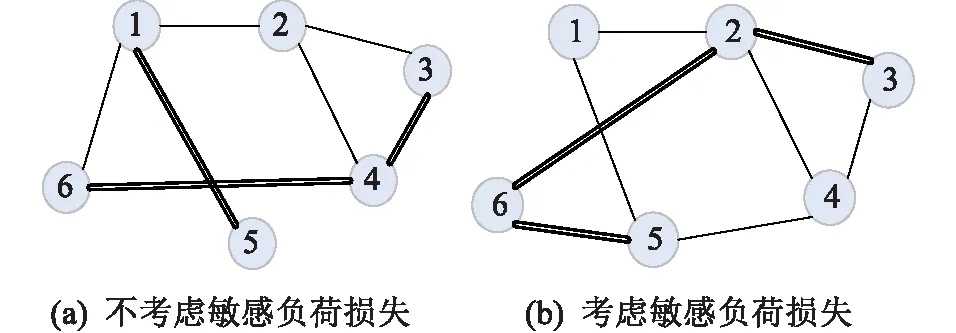
圖7 網架規劃結構Fig.7 Grid line planning topology

當考慮敏感負荷損失因素時，網架規劃方案與用不考慮敏感負荷損失得出的方案相比，雖然網損和線路投資總費用有所增加，但降低了配網失負荷的風險，并且在將敏感負荷損失量轉化為相應經濟損失后，綜合投資費用從3 605.1萬元下降至3151.0萬元，提高了配網規劃的經濟性。因此在進行網架規劃時，考慮電壓暫降導致的敏感負荷損失量是合理且必要的。

5 結語

可再生能源發電受天氣和季節的影響比較大，抗干擾能力較差，大量新能源接入電網，對電網電壓產生大幅擾動。針對變頻器接入型負荷的適應性，本文總結了多種主要敏感設備的電壓耐受特性，建立了變頻調速電機的仿真模型，并計算了變頻調速器在VTC不確定區域內受電壓波動影響的負荷損失概率。在原有風險規劃的基礎上，提出了考慮電壓波動下敏感負荷損失的配電網規劃模型，提高了規劃方案的合理性。以6節點系統電網為例，利用粒子群算法對考慮敏感負荷損失的風險規劃模型進行求解。與不考慮敏感負荷損失時的規劃方案相比，降低了敏感負荷損失的風險，提高了配網規劃方案的經濟性。