溝槽式高填黃土明洞洞頂垂直土壓力統一計算方法
李 盛,劉亞朋,何 川,王 煥,王起才,馬 莉
(1.蘭州交通大學 道橋工程災害防治技術國家地方聯合工程實驗室,甘肅 蘭州 730070;2.西南交通大學 交通隧道工程教育部重點實驗室,四川 成都 610031;3.中鐵十四局集團有限公司,山東 濟南 250014;4.蘭州工業學院 土木工程學院,甘肅 蘭州 730050)
我國黃土高原地區溝多坡陡、地形起伏破碎、土地資源緊缺且分布不連續。為了緩解城市用地緊張、滿足鐵路建設中較高的線性要求,填溝造地,整合土地資源。這將不可避免對溝槽式鐵路明洞進行高回填。然而,目前國內外尚沒有適合于溝槽式明洞土壓力的統一計算理論。合理計算作用于溝槽式明洞洞頂土壓力,一方面,可以優化新建鐵路明洞結構,使設計更加合理;另一方面,一定程度上減少竣工后可能出現的病害,增加鐵路運營中的安全性。
高填方土壓力最早由Marston提出,并以散體極限平衡條件推導得到高填方涵洞(管)Marston土壓力公式[1];隨后,Handy[2]用摩爾應力圓求解出側向土壓力系數;Kellogg等[3-5]將該理論應用到地下構筑物垂直土壓力的推導計算中;顧安全、王曉謀[6-9]根據模型試驗,提出是否采取減載措施的土壓力計算公式;鄭俊杰、楊錫武[10-13]分別將填土視為線彈性體與非線性情況推導出線彈性與非線性土壓力計算理論和方法;以上研究主要針對高填方涵洞(管),對于高填方明洞結構,文獻[14]提出了考慮邊坡坡角的高填黃土明洞土壓力的計算方法,但邊坡較平坦的情況并不適用。本文在文獻[14]的基礎上,考慮填土沉降滑裂面,推導適用于大、小坡角情況下的溝槽式高填黃土明洞洞頂土壓力統一計算方法。以某鐵路溝槽式高填明洞工程為例,將數值模擬結果與計算公式結果進行對比驗證,并探討小坡角情況下填料性質、溝槽與明洞寬度比等因素對高填黃土明洞土壓力變化規律的影響。
1 垂直土壓力理論
目前,溝槽式高填黃土明洞洞頂土壓力計算公式適用于兩側邊坡較陡的情況,即土體在自重和上覆荷載作用下,外側土柱會沿著邊坡向下滑動,外土柱的一部分壓力通過土體剪切作用轉移至邊坡及內土柱上。明洞頂受到的垂直土壓力由填土自重壓力和內土柱所受的附加壓力2部分構成。
假定明洞洞頂受均布荷載,可得到明洞洞頂受到的垂直土壓力σ為[14]
(1)
式中:γ為填土的重度;H為總填土高度;h為明洞凸出地面的高度;F為內土柱所受的附加荷載;D為明洞寬度。
附加荷載F是由內外土柱間沉降差引起的。根據朗肯土壓力理論及力的平衡原理,深度y處內外土柱剪切力τ2可由外土柱受到的土壓力q推得
τ2=αq+β
(2)
其中,
α=katanφ
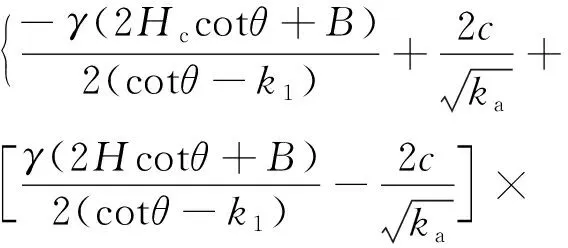
式中:ka為填土側壓力系數;c為填土黏聚力;φ為填土的內摩擦角;θ為邊坡坡角;B為溝槽寬度;b為坡腳到明洞側面的距離,δ為邊坡與填土之間的摩擦角;Hc為等沉面高度。
對式(2)進行積分即可得到附加荷載F為
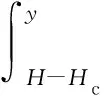
(3)
聯立求解式(1)和式(3)可得明洞洞頂土壓力為
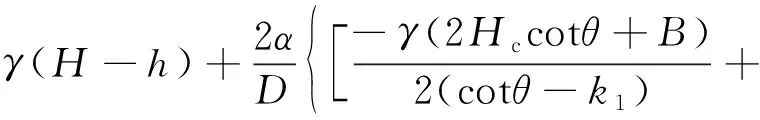
(4)
然而,當邊坡坡角θ較小時,土體在自重和上覆荷載作用下,土中會產生滑裂面,外側土柱將會沿著滑裂面向下滑動,因此,式(4)僅適用于溝槽邊坡坡角較大的情況。
2 統一的垂直土壓力計算方法
2.1 小坡角溝槽明洞洞頂土壓力計算方法
為了得到同時滿足大、小坡角的溝槽式高填明洞洞頂垂直土壓力計算公式,依據文獻[14—15],基于巖土力學原理,建立小坡角溝槽高填黃土明洞土壓力計算模型,如圖1所示。圖中:τ1為滑裂面上的剪切力。
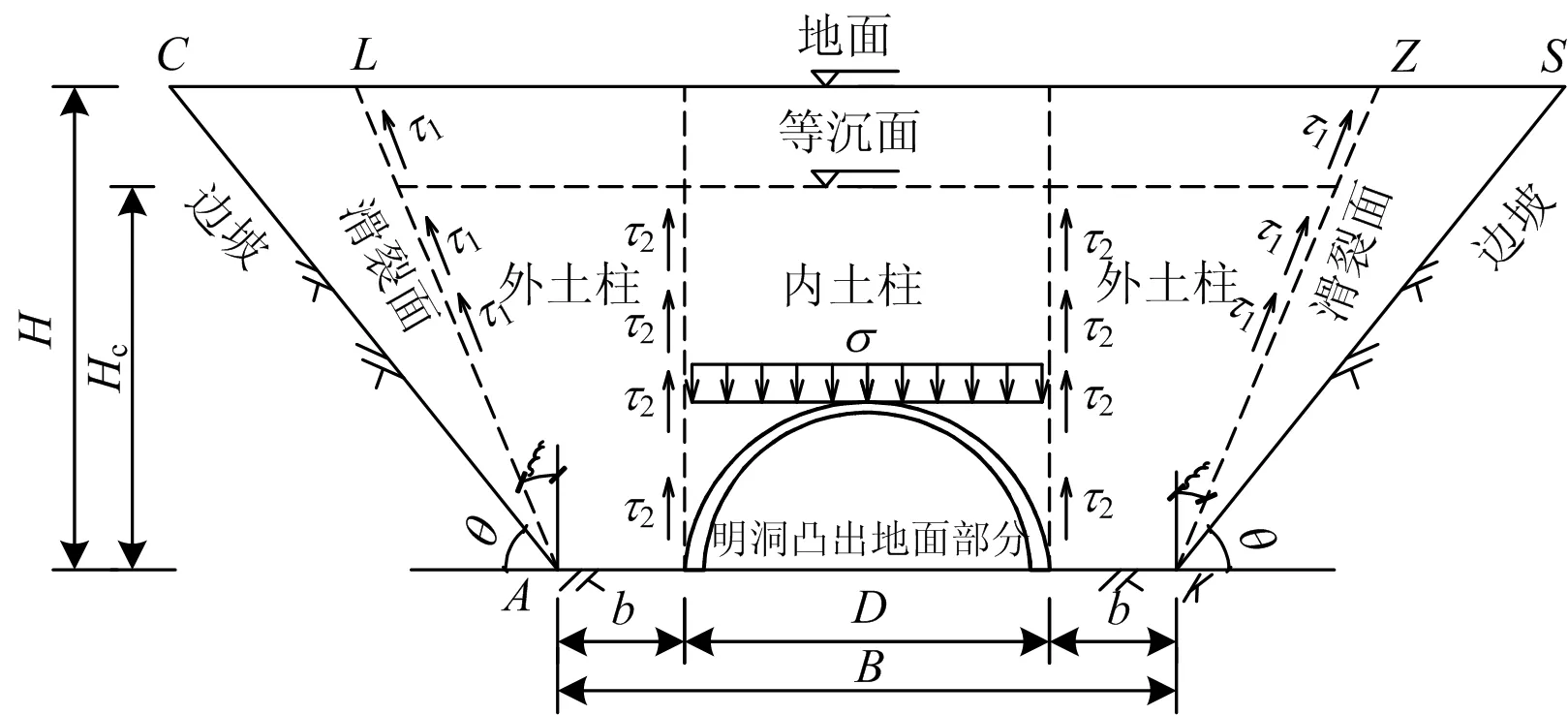
圖1 明洞洞頂土壓力理論分析模型
當邊坡坡角θ較小(θ≤90°-ξ,ξ為臨界傾斜角)時,土體在自重和上覆荷載作用下,土中會產生滑裂面AL和KZ。計算明洞周圍土壓力時,僅需要考慮滑裂面內側土體對明洞的作用力。在計算外土柱所受土壓力q時,剪切力不再由兩側邊坡直接作用,而是由與滑裂面相接觸的土體ALC和KZS提供支撐剪切作用。
已有研究表明[15],ξ=f(δ,φ,ω),其中ω為填土面與水平面的夾角。當δ=φ時,ξ=45°-φ/2+ω/2-arcsin(sinω/sinφ)/2。由于填土面水平,ω=0,則ξ=45°-φ/2。
以文獻[14]中的推導過程為基礎,可得到外土柱所受的土壓力為
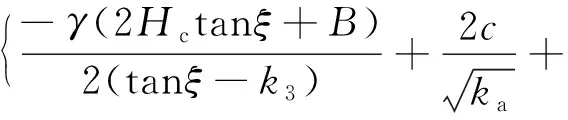
(5)
其中,
聯立式(1)、式(2)和式(5),可得小邊坡坡角下的明洞洞頂垂直土壓力為
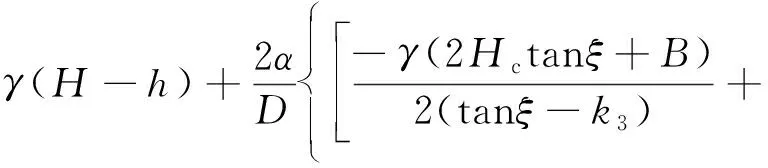
(6)
2.2 統一計算方法
通過引入系數m,t1和t2,對式(4)和式(6)整理,得到明洞洞頂垂直土壓力統一計算公式為
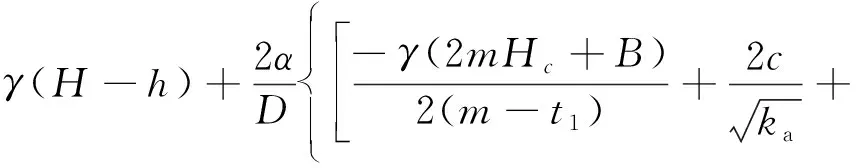
(7)
當θ>90°-ξ時,式(7)中m=cotθ,t1=k1,t2=k2;當θ≤90°-ξ時,式(7)中m=tanξ,t1=k3,t2=k4。
3 統一計算方法驗證
以某鐵路溝槽式高填明洞為例,采用統一計算公式(7)計算明洞洞頂垂直土壓力,并采用有限元軟件對其進行模擬分析,驗證本文計算方法的正確性。
模型網格劃分以平面四邊形為主,三角形為輔。模型兩側定義水平方向的邊界約束,底部定義水平和豎直方向的約束。通過定義時間步的方法模擬分層填筑過程,計算每個時間步的應力場、位移場。明洞、邊坡采用理想彈性材料模型;黃土、明洞地基采用莫爾—庫侖理想彈塑性模型。邊坡及明洞結構與填土的接觸關系采用庫侖摩擦定律實現,即τcrit=μp,其中τcrit為極限剪應力,μ為摩擦系數,p為法向接觸應力。以小邊坡坡角θ=40°為例進行說明,各材料計算參數見表1,計算模型如圖2所示。
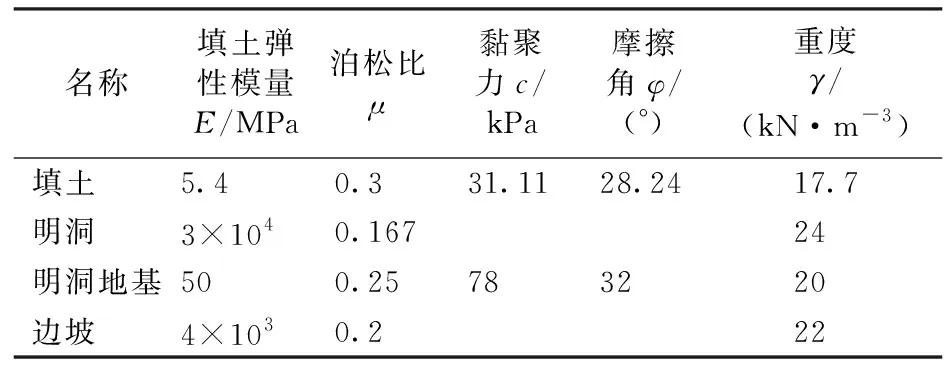
表1 計算參數
不同小坡角情況下,明洞寬度范圍內洞頂土壓力分布有限元計算結果如圖3所示。
由圖3可知,邊坡坡角θ=10°,20°,30°和40°時,明洞頂土壓力大致呈“拋物線”分布,且隨著邊坡坡角的增加而減小。以θ=40°為例,采用荷載等效方法,將明洞洞頂土壓力數值模擬計算結果等效為均布荷載,得到等效計算圖如圖4所示。

圖2 1/2計算模型網格劃分
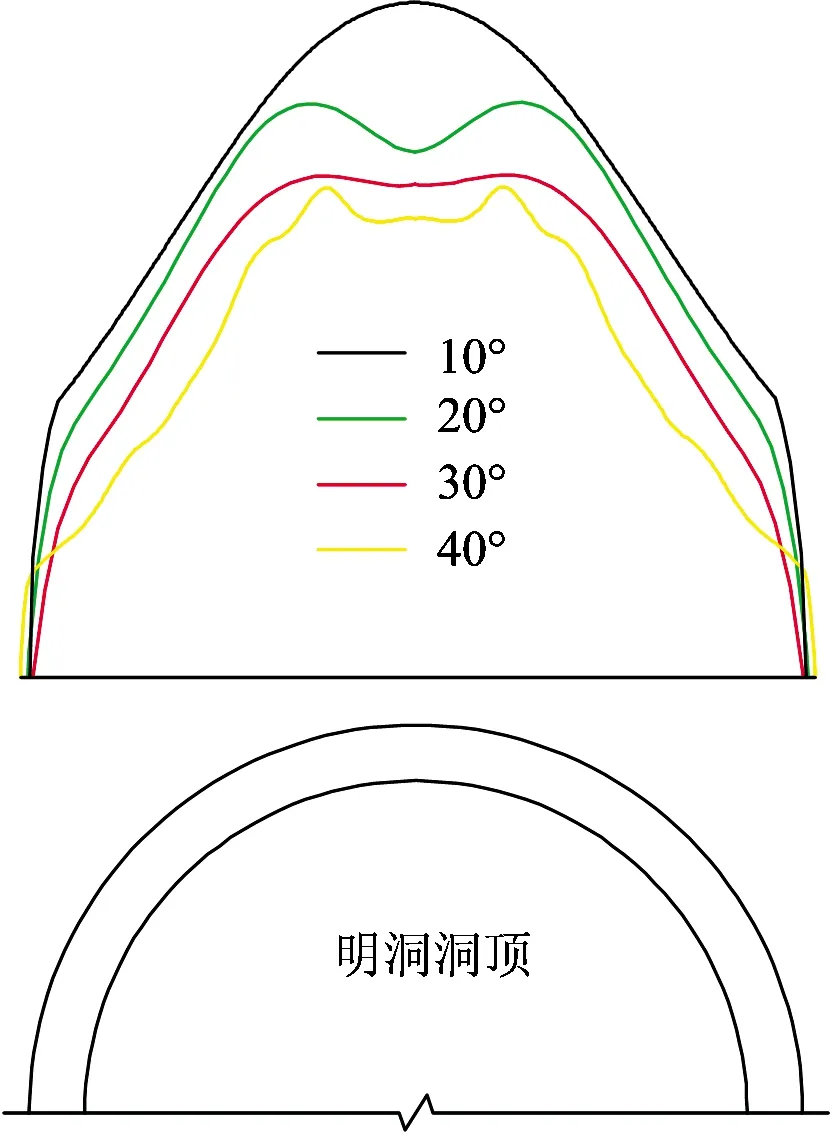
圖3 明洞洞頂土壓力分布有限元計算結果
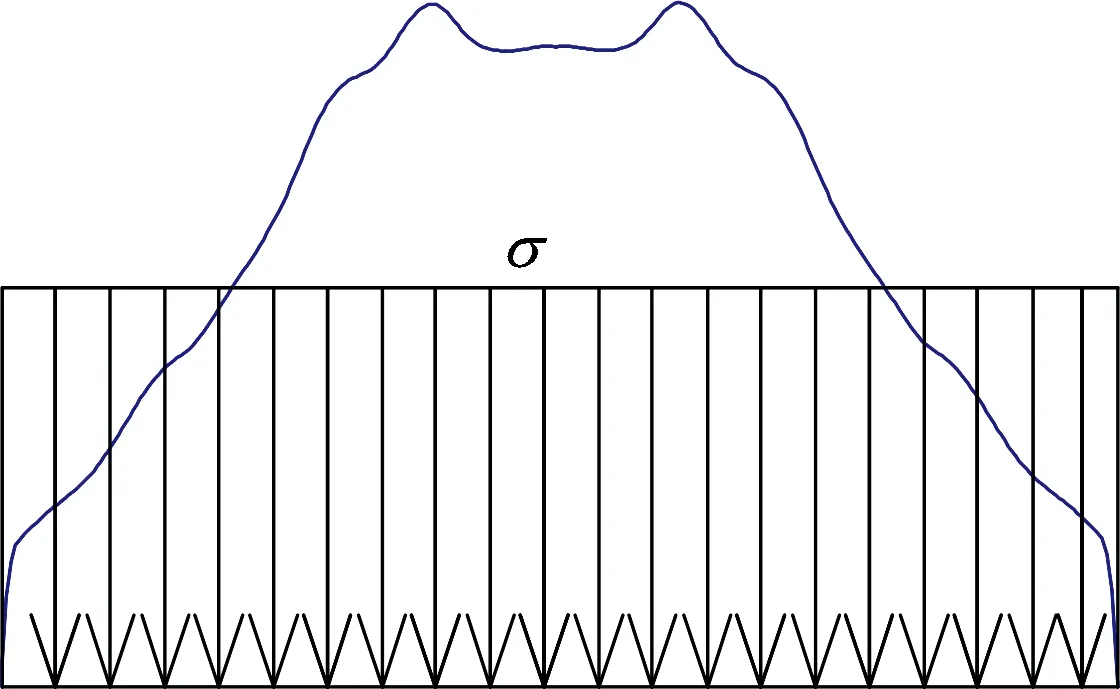
圖4 土壓力等效計算圖(θ=40°)
圖5給出了數值計算等效荷載值、文獻[14]計算值和本文統一公式(7)計算值的比較結果。
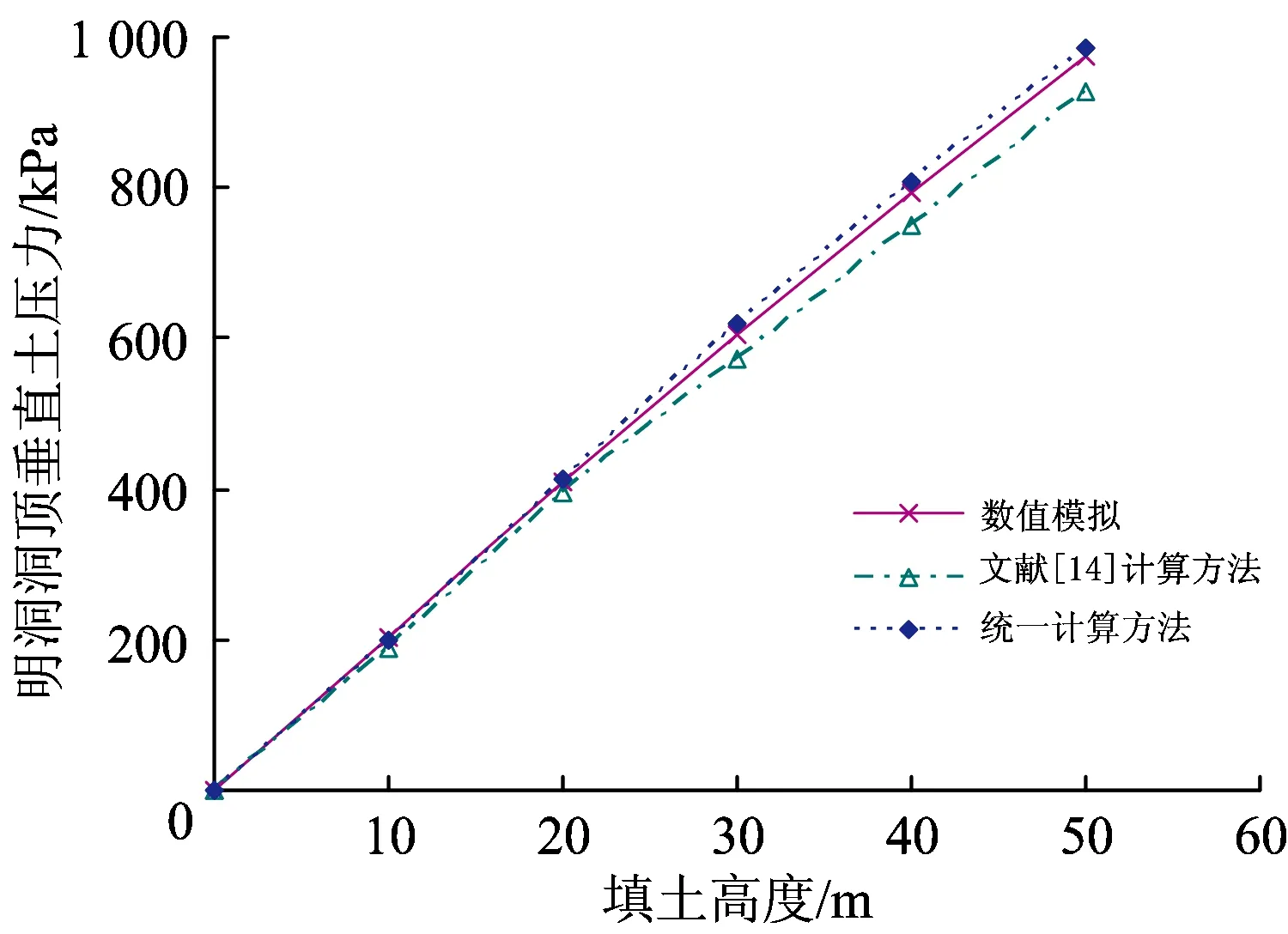
圖5 明洞洞頂垂直土壓力隨填土高度的變化規律
由圖5可知,統一計算方法所得到的明洞洞頂垂直土壓力變化規律與文獻[14]計算方法、數值模擬得出的規律完全一致,即明洞洞頂土壓力隨著填土高度的增加而增加;在計算結果上,統一計算方法得出的土壓力比文獻[14]計算方法得出的結果大,且與有限元計算的結果更為接近,因此,驗證了統一計算方法的合理性。本文計算結果與有限元數值模擬結果最大相對誤差為2.63%,而文獻[14]計算結果與數值模擬結果的最大相對誤差7.64%。這是由于文獻[14]計算方法計算小坡角溝槽明洞洞頂土壓力時,未考慮滑裂面的影響,突出了邊坡的作用,使得土壓力的計算結果偏小。實際上,溝槽邊坡坡度較小時,邊坡影響較小,填土沉降過程中,會產生新的滑裂面,明洞周圍土壓力計算僅需考慮滑裂面內側土體對明洞的作用力,統一計算方法綜合考慮了大小邊坡坡角的情況,因此,該計算結果更為接近數值模擬結果。
4 影響因素分析
為了明確影響小坡角溝槽高填黃土明洞洞頂土壓力的參數敏感性,本文采用明洞洞頂土壓力分析填料性質(填料內摩擦角φ,黏聚力c,填土模量E)、溝槽與明洞寬度比B/D等參數的影響程度。
基本參數取值:明洞洞頂填土高度H=5,10,…,50 m,邊坡坡角θ=20°,填料內摩擦角φ=28°,黏聚力c=30 kPa,壓縮模量E=5 400 kPa,B/D=1.1,h/D=1.17。
4.1 填料性質的影響
1)內摩擦角
分別取填料內摩擦角φ=10°,20°,30°和40°進行計算,得到的明洞洞頂土壓力如圖6所示。由圖6可以看出,當填土高度一定,10°≤φ≤20°和30°≤φ≤40°時,土壓力隨內摩擦角的增加變化不大,平均變化率不到1.4%;當20°<φ<30°時,隨著填土高度的增大,兩者土壓力相差率逐漸增大,由填土高5 m時的相近變為填土高50 m時的相差7.8%。這就說明,小坡角溝槽明洞土壓力在填土較低時,可以忽略內摩擦角的影響;但在填土較高、內摩擦角在20°~30°之間變化時,明洞洞頂土壓力相差較大。
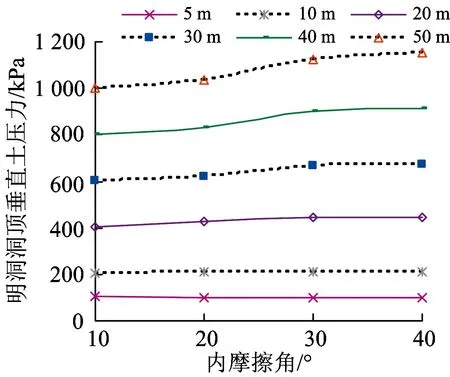
圖6 不同填土高度時明洞洞頂土壓力隨內摩擦角變化曲線
2)黏聚力
分別取黏聚力c=30,40,60和80 kPa進行計算,得到的明洞洞頂土壓力見表2。由表2可知,填土高度一定時,黏聚力增大或減小對土壓力影響很小,平均變化不到1.4%,土壓力基本不變;這就說明,溝槽坡度較小時,粘聚力變化對高填土壓力的影響可以忽略。
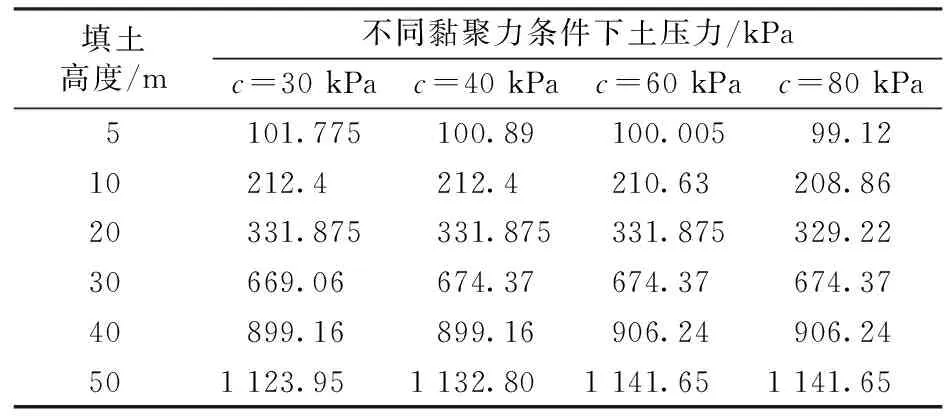
表2 不同黏聚力時明洞洞頂土壓力
3)填土模量
分別取填土模量E=5,10,20和50 MPa進行計算,得到的明洞洞頂土壓力隨填土高度的變化曲線如圖7所示。由圖7可知,當填土高度較低(H≤10 m),填土高度一定時,隨著填土模量的增加,明洞洞頂土壓力變化不大,平均變化率僅為2.4%;但是,當填土高度10 圖7 不同填土模量時明洞洞頂土壓力隨填土高度變化曲線 分別取溝槽與明洞寬度比B/D=1,1.5,2.0和2.5進行計算,得到的明洞洞頂土壓力見表3。從表3中可以看出,填土高度一定時,B/D的變化對土壓力影響很小,平均變化率不到1.6%,明洞洞頂土壓力基本不變。由此表明,溝槽坡度較小時,溝槽與明洞寬度比對明洞洞頂土壓力的影響可以忽略不計。 表3 不同槽寬比時明洞洞頂土壓力 (1)綜合考慮小坡角情況下的土體滑裂面與大坡角情況下的邊坡作用,提出了溝槽式高填黃土明洞洞頂垂直土壓力統一計算公式。該公式計算結果與有限元計算結果最大相對誤差為2.63%,文獻[14]計算方法與數值模擬結果的最大相對誤差為7.64%,驗證了本文計算方法的正確性,可為大、小邊坡坡角溝槽式明洞設計提供參考。 (2)小坡角溝槽情況下,隨著填土高度的增加,邊坡對洞頂土壓力的作用相對弱化,明洞洞頂垂直土壓力由滑裂面內側土體提供,大致呈“拋物線”分布,且隨著邊坡坡角的增加而減小。隨著填土模量增大,土體壓縮相對變形量減小,明洞洞頂土壓力隨之變小。相比而言,填土內摩擦角、黏聚力以及溝槽與明洞寬度比對明洞洞頂垂直土壓力的影響不明顯。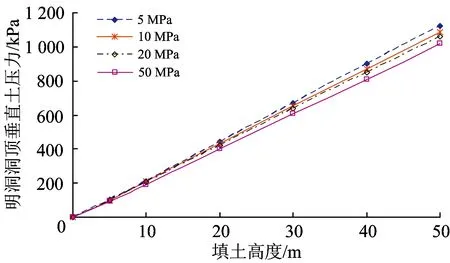
4.2 溝槽與明洞寬度比B/D的影響
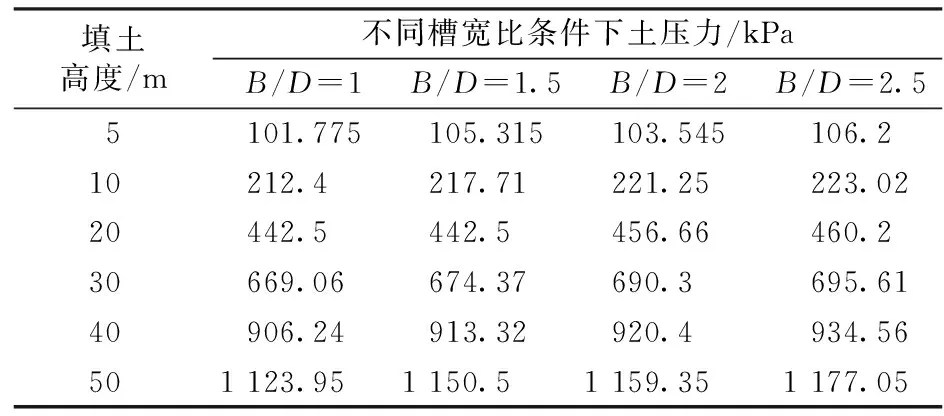
5 結 論

