微型電動貨車車架分析
周輝,趙海軍,程廣偉 ,宋偉志 ,姚永玉
(1.洛陽理工學院機械工程學院,河南洛陽 471023;2.天津職業技術師范大學汽車與交通學院,天津 300222)
0 引言
當今能源危機、大氣污染嚴重,特別是城市區域,交通擁堵、人員密集,各地相繼推出限行政策,傳統微型貨運車輛在城區的使用受到了諸多限制,對城區物流影響較大。微型電動貨車對于緩解城市交通污染,提高城市物流運輸效率,有非常現實的意義。而車架作為主要承載部件,需承受扭轉、彎曲、振動沖擊等復雜載荷,其足夠的強度、剛度及動態特性對于保證整車使用性能及安全性十分重要[1-2]。文中以在某傳統微型貨車基礎上改裝的電動貨車為基礎,對改裝后的車架進行受力分析及有限元仿真,初步驗證了車架的強度和剛度,進行了模態和諧響應分析,可為車架改進提供依據,以保證車輛的可靠性。
1 車架有限元模型建立
建立改裝后的微型電動貨車車架三維模型,如圖1所示。
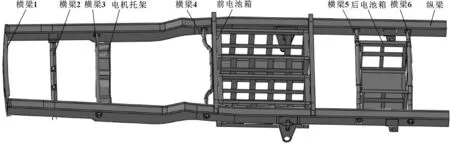
圖1 車架三維模型
該車架為邊梁式車架,由2根縱梁和6根橫梁構成,縱橫梁之間采用焊接。車架材料為B510L鋼,縱梁為箱形截面,前橫梁為槽形截面,其余橫梁為圓形截面。其中縱梁厚度為3.5 mm,第一橫梁厚度為2.5 mm,其余橫梁厚度為4 mm。改裝車架去掉了原車底盤發動機部分及發動機懸置部分,增加電動機托架和電動機及其控制部分。在車架中部和后部用角鐵(Q345)焊接電池箱,前電池箱通過2根厚度為4 mm的槽鋼(Q345)固定在車架兩縱梁上,后電池箱焊接在原固定燃油箱的橫梁上。
在前處理軟件中,將車架三維模型導入ABAQUS進行分析。因為車架各部件厚度遠小于其整體結構尺寸,應用殼單元類型進行分析具有較高的準確度,所以車架結構采用殼單元模擬[3]。車架各部件連接時,采用焊接和螺栓連接及鉚接,在建立有限元模型時不考慮具體連接性能,均采取剛性綁定約束。前懸架為麥弗遜懸架,用彈簧單元簡化;后懸架為鋼板彈簧懸架,采用剛性梁單元和彈性單元模擬。定義車架材料及各部件壁厚,材料屬性如表1所示。網格劃分以S4R四邊形單元為主,S3三角形單元為輔,整個模型含24 832個節點、25 078個單元,其中四邊形單元24 832個。有限元模型如圖2所示。

表1 材料屬性
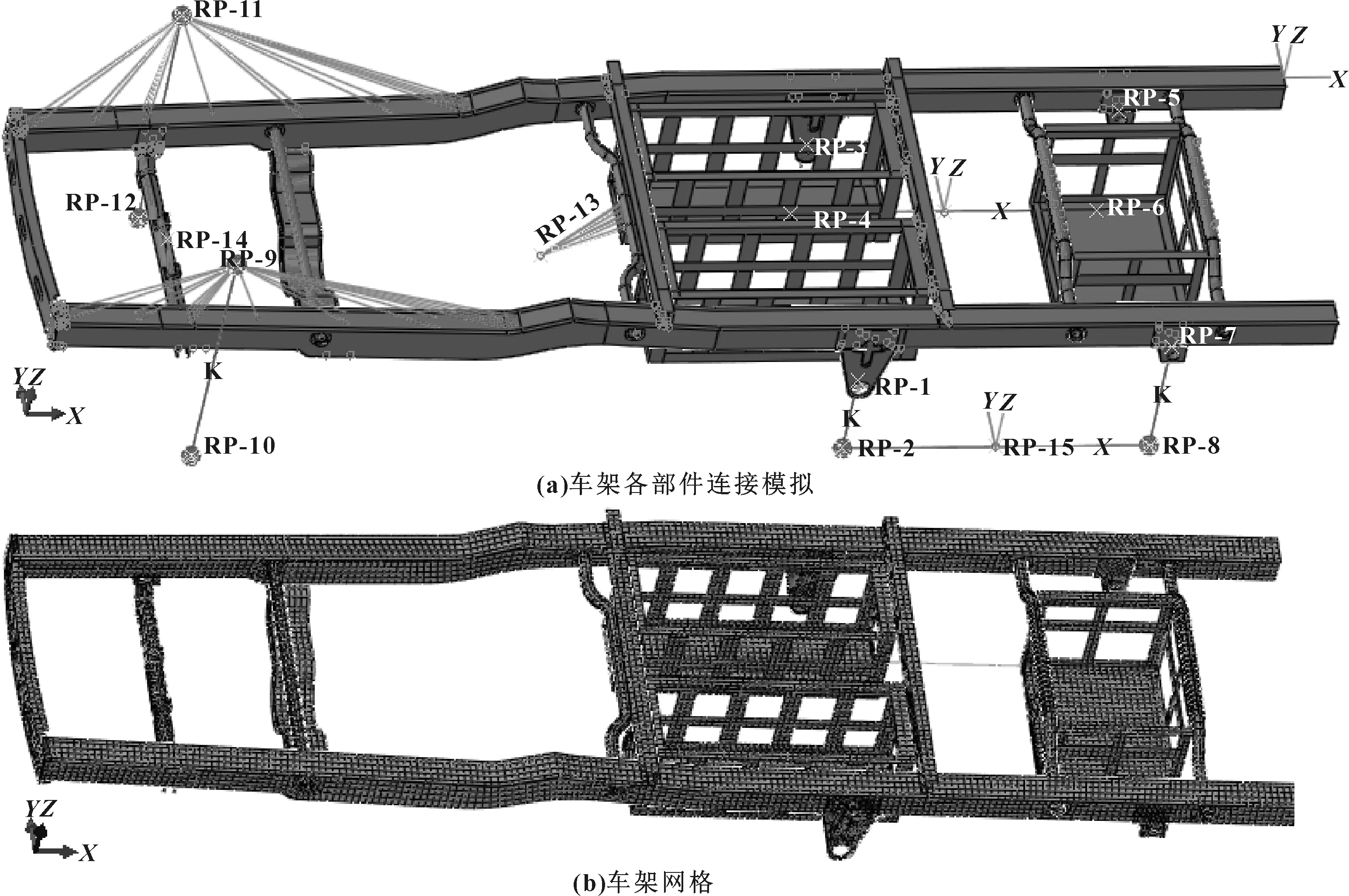
圖2 車架有限元模型
2 車架靜力學分析
2.1 靜力學分析基礎
文中所研究為線性靜力學,不考慮慣性和阻尼,其基本有限元方程[4]為:
KU=F
(1)
式中:K為模型剛度矩陣;U為節點位移陣列;F為模型受外界力矩陣。
(1)強度計算基礎
車架靜強度校核根據第四強度理論,采用Von Mises等效應力來進行[4]。
Von Mises等效應力公式為:
(2)
強度合格條件為:
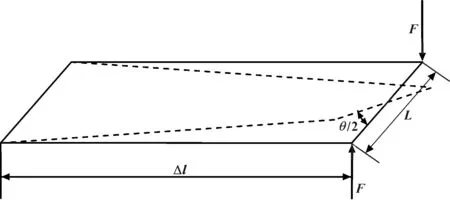
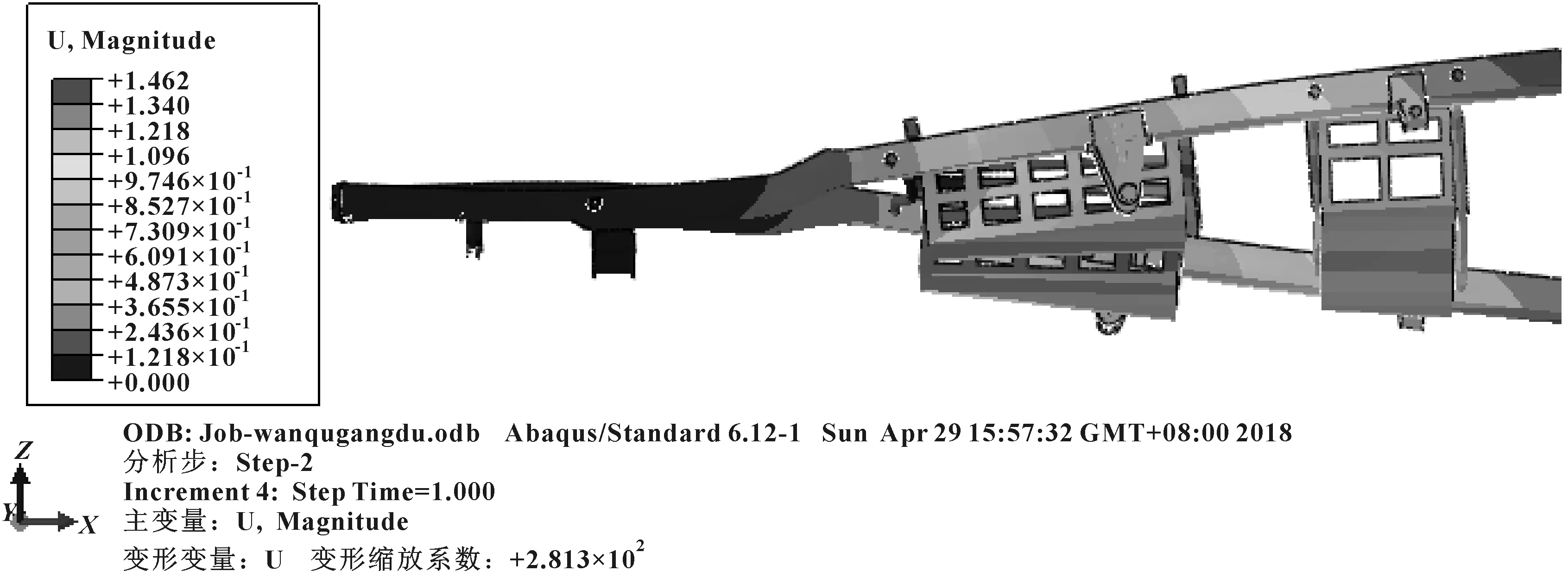
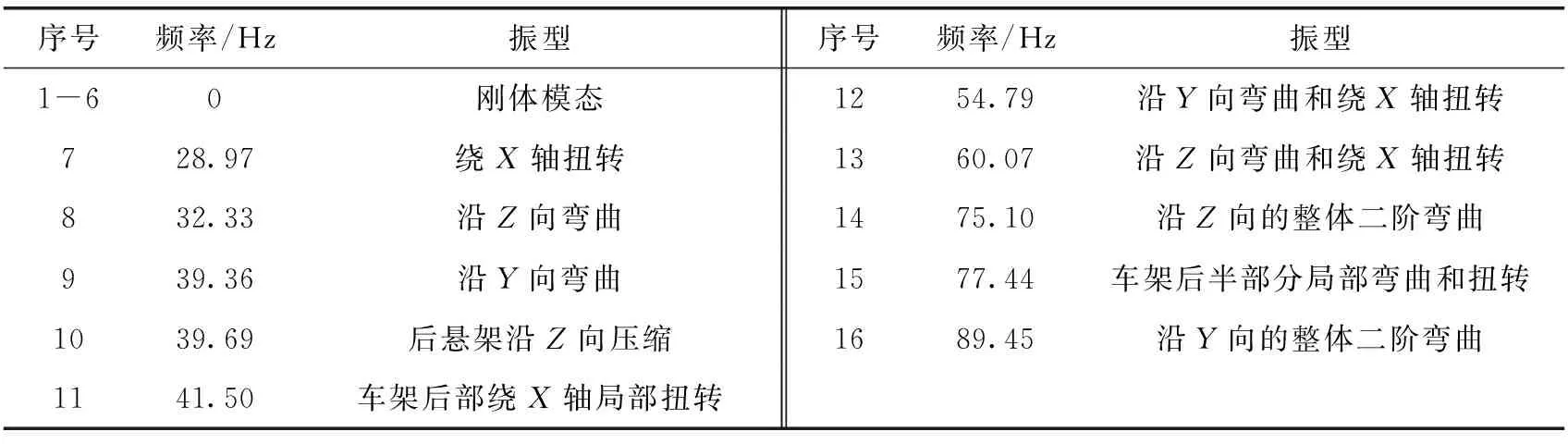
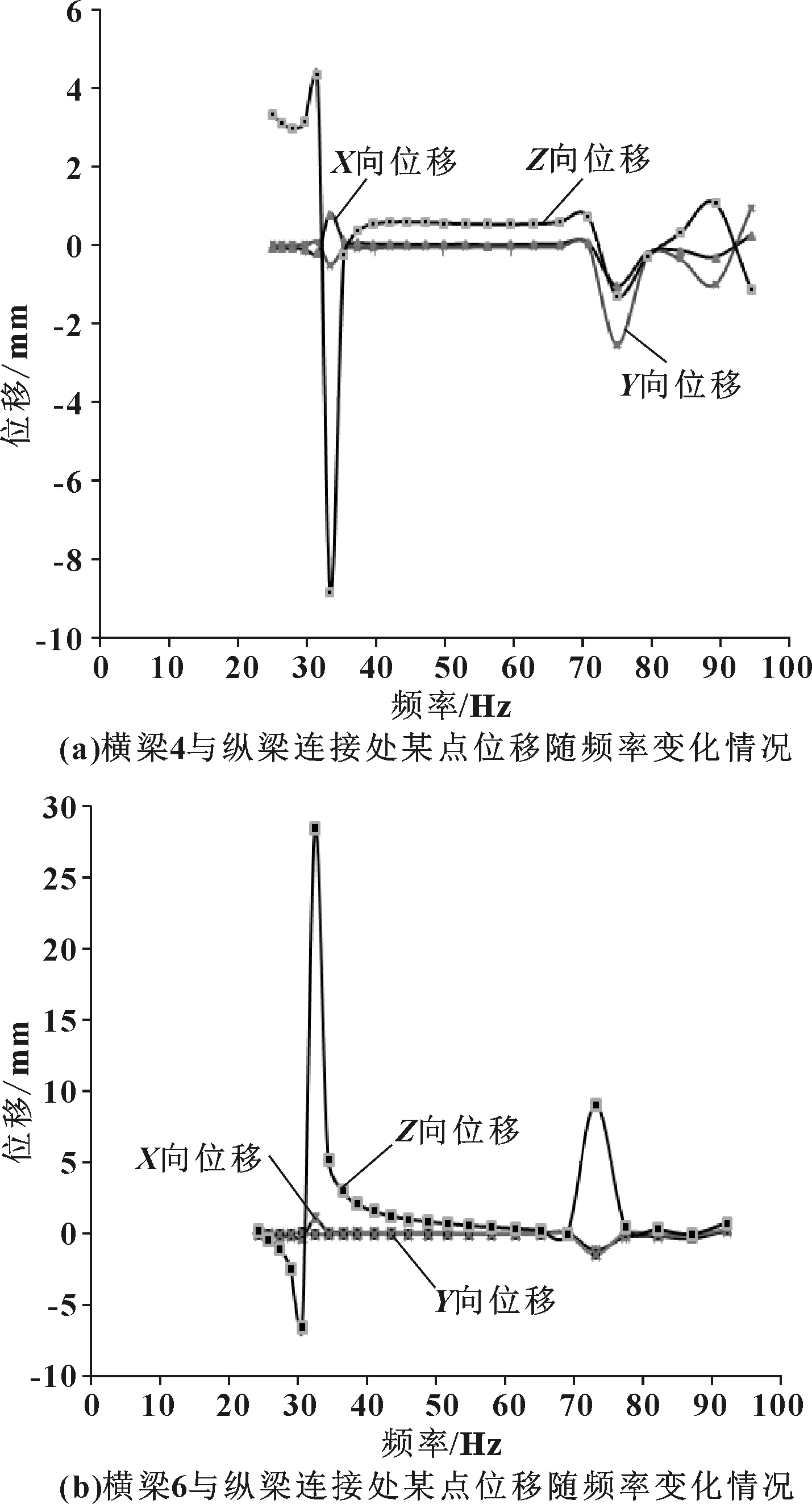
σr (3) 式中:σr為Von Mises應力;σs為材料屈服極限;n為安全系數。 (2)剛度計算基礎 ①彎曲剛度 計算車架彎曲剛度時,將其簡化為簡支梁形式,如圖3所示,在車架中部施加豎直向下的集中載荷,得出車架變形量dzmax。車架彎曲剛度根據式(4)求解[1]: (4) 式中:K′為彎曲剛度;Δl為兩支撐點之間距離;F為豎直方向集中載荷;dzmax為撓度。 圖3 車架彎曲剛度計算簡圖 ②扭轉剛度 計算扭轉剛度時,將車架簡化為4根梁構成的矩形,約束前方兩端點的豎直平動自由度,后方兩端點施加方向相反大小相等的集中載荷,得出車架變形量。車架扭轉剛度根據式(5)求解: (5) M=FL (6) (7) 式中:CT為扭轉剛度;L為左右受力點之間距離;F為豎直方向集中載荷;d為撓度;θ為扭轉角。 車架扭轉剛度計算簡圖如圖4所示。 圖4 車架扭轉剛度計算簡圖 車架載荷包括自重和承載各總成重力。承載各總成主要包括電動機及其控制系統、動力電池總成、變速器總成、車廂、駕駛室、貨物、乘員等。各載荷重力及有限元分析時處理方式如表2所示。 表2 車架靜態載荷及處理方式 車輛在定型試驗中必須要模擬典型工況以確定車輛的行駛可靠性,通常包含彎曲、扭轉、緊急制動和轉彎4種工況。其中彎曲和扭轉工況反映了車架的結構強度,文中主要分析這兩種工況。其邊界條件定義如表3所示。 表3 扭轉、彎曲工況邊界條件 (1)彎曲工況 彎曲工況以車輛滿載情況進行分析,考慮車輛行駛狀態,進行校核時要乘以動載系數。相關資料表明,動載系數一般取2~2.5,文中取2.5[5]。 彎曲工況車架應力情況如圖5所示,變形情況如圖6所示。從圖中可得,最大變形出現在電機托架處為1.403 mm;應力最大值出現在電機托架彎曲點,達到83.82 MPa,乘以動載系數后為209.55 MPa小于許用應力,滿足強度要求。除此之外,車架整體受力均勻,且等效應力大多在20 MPa以下,針對電機托架應力集中處,可在背部焊接加強肋。 圖5 彎曲工況車架應力圖 圖6 彎曲工況車架變形云圖 (2)扭轉工況 扭轉工況以車輛滿載情況進行分析,受力及前輪邊界條件和彎曲工況相同,左右后輪分別施加±20 mm位移約束。電動貨車主要在市區道路工作,在扭轉工況下車速一般較低,動載系數一般取1.3[7]。經計算,車架滿載扭轉工況下的變形情況如圖7所示,左后懸架位移最大,達到30.71 mm,左右車架縱梁變形量差值7.68 mm。車架所受應力情況如圖8所示,最大應力出現在后懸架前支座處,應力達到222.4 MPa,是因為在建立有限元模型時,將懸架與支座直接進行了剛性耦合造成了應力集中。實際鋼板彈簧與支座之間連接允許相對滑動,可避免應力集中問題。除此之外,焊接前電池箱的槽鋼和縱梁連接處,以及焊接后電池箱的第5、第6橫梁處受力相對較大,應力值在 75~130 MPa之間。考慮動載系數后應力值在97.5~169 MPa之間,小于許用應力。 圖7 扭轉工況車架變形圖 圖8 扭轉工況車架應力圖 (1)彎曲剛度 約束前懸架螺旋彈簧與車架連接處XYZ的平動自由度,約束后懸架兩支座中間與后輪軸線對應處支座的YZ兩個方向平動自由度,釋放X方向自由度。如圖3所示,將車架簡化為簡支梁,在約束的前后兩支座中間左右縱梁上分別施加500 N的作用力。彎曲變形情況如圖9所示,dzmax為0.48 mm,Δl為2 487.2 mm,根據公式4計算得到彎曲剛度K′為3.3×105N·m2。某電動車車架彎曲剛度[5]為99 307 N·m2,與之相比文中所研究改裝后的電動貨車剛度值更為合理。 圖9 彎曲剛度車架變形圖 (2)扭轉剛度 計算扭轉剛度時,約束前懸架螺旋彈簧與車架連接處XYZ的平動自由度,在左右縱梁后懸架兩支座中間與后輪軸線對應處支座上施加方向相反的500 N作用力。車架扭轉變形情況如圖10所示,受力點相對位移為2.92 mm,兩受力點之間距離為976 mm。根據式(5)—(7)計算得,車架所受轉矩M為488 N·m,扭轉角為0.002 99 rad,扭轉剛度為163 210.7 N·m/rad。 圖10 扭轉剛度車架變形圖 為保證電動貨車承載的可靠性,其車架不僅要有足夠的靜態強度和剛度,還需要有良好的動態性能。汽車在行駛過程中不僅要承受路面經車輪傳遞的隨機振動[6],還要承受由電動機及變速器等工作時產生的周期性受迫振動。若車架某階固有頻率與其所受激振頻率接近時,可能會發生共振,產生劇烈振動而造成車架過早損壞。因此,通過模態分析得到車架各階固有頻率為設計提供參考,避開外部激振頻率,可以有效避免該問題發生。 完全按照車架的實際工況約束邊界條件來進行模態分析,對于多自由度復雜系統來說是比較困難的[7]。從理論上講,任意邊界條件約束下的動態特性可以由自由邊界條件下模態參數經計算得到[8]。因此,文中計算了自由邊界條件下的車架模態,采用的方法為Lanczos法,結果如表3所示。 表3 車架前16階去除前6階固有頻率及振型 汽車在行駛過程中承受路面經車輪傳遞的隨機振動頻率一般為20 Hz左右[6]。電動機運轉時對車架的激勵作用一般很小,不予考慮[7]。車架前16階振型頻率在28.9~90 Hz左右,低階模態與路面所產生的隨機激振頻率較接近,有可能產生共振。 計算車架在簡諧激勵下的穩態響應,求出其關鍵節點的位移和應力變化情況,以驗證車架改裝的合理性,并為后續改進提供參考。諧響應分析時車架所受載荷和靜態分析時相同,簡諧激勵通過前輪和后輪的Z向簡諧位移約束實現。前后輪采用相同頻率和振幅的簡諧激勵,后輪激勵的相位角比前輪推遲π/6。電動貨車主要在市區行駛,路面情況較好,激勵的幅值取為20 mm。考慮車架前16階模態(去除前6階)頻率范圍,取激勵頻率范圍為25~95 Hz,間隔為2.5 Hz,共29個激振頻率。 由于電池重力較大,前后電池箱固定位置的諧振情況是需要關注的。在前后電池箱固定位置的縱橫梁連接處選擇相應節點來進行分析,其位移隨激勵頻率的變化情況如圖11所示。由圖11(a)可知,橫梁4與縱梁連接處節點位移在X向位移最大值為1 mm,Y向位移最大值為2.5 mm,且對應頻率均在75 Hz附近,該頻率大約對應車架14階模態頻率。Z向位移在低頻階段均較大,最大值出現在33 Hz附近,位移為8.8 mm,對應車架8階模態頻率。由圖11(b)可知,橫梁6與縱梁連接處節點位移在X向位移最大值為1.2 mm,Y向位移最大值為1.5 mm,對應頻率也均在75 Hz附近。Z向位移在33 Hz下最大達到28.5 mm,75 Hz下達到9 mm。由此可知,所關注的縱橫梁連接處,在33 Hz和75 Hz時諧振幅度較大。 圖11 位移隨激勵頻率變化情況圖 在傳統微型貨車基礎上建立了改裝的電動貨車車架有限元模型,充分考慮了車架結構特點,合理處理了各部件之間的相互作用關系。計算了電動貨車車架強度和剛度等靜態性能,計算了車架自由模態并進行了諧響應分析。綜合得出如下結論: (1)按照靜力學分析理論,車架彎扭強度均滿足許用應力要求,彎扭剛度適中。但第5、第6橫梁所受應力較大,可適當增加兩橫梁厚度。 (2)車架低階自由模態頻率與路面激勵頻率較接近,路面經車輪產生的激勵可能會造成車架劇烈的振動。針對該情況,可適當調整電池箱固定位置。 (3)電池箱安裝位置的縱橫梁連接點在33 Hz和75 Hz的激振頻率下可能會發生共振。應對車架結構進行優化以避免共振發生。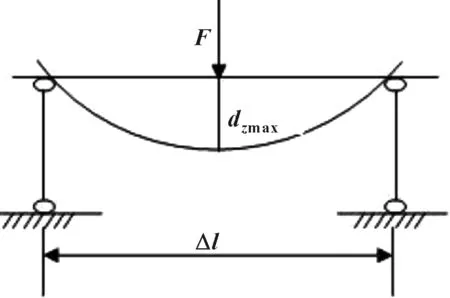
2.2 車架靜態載荷
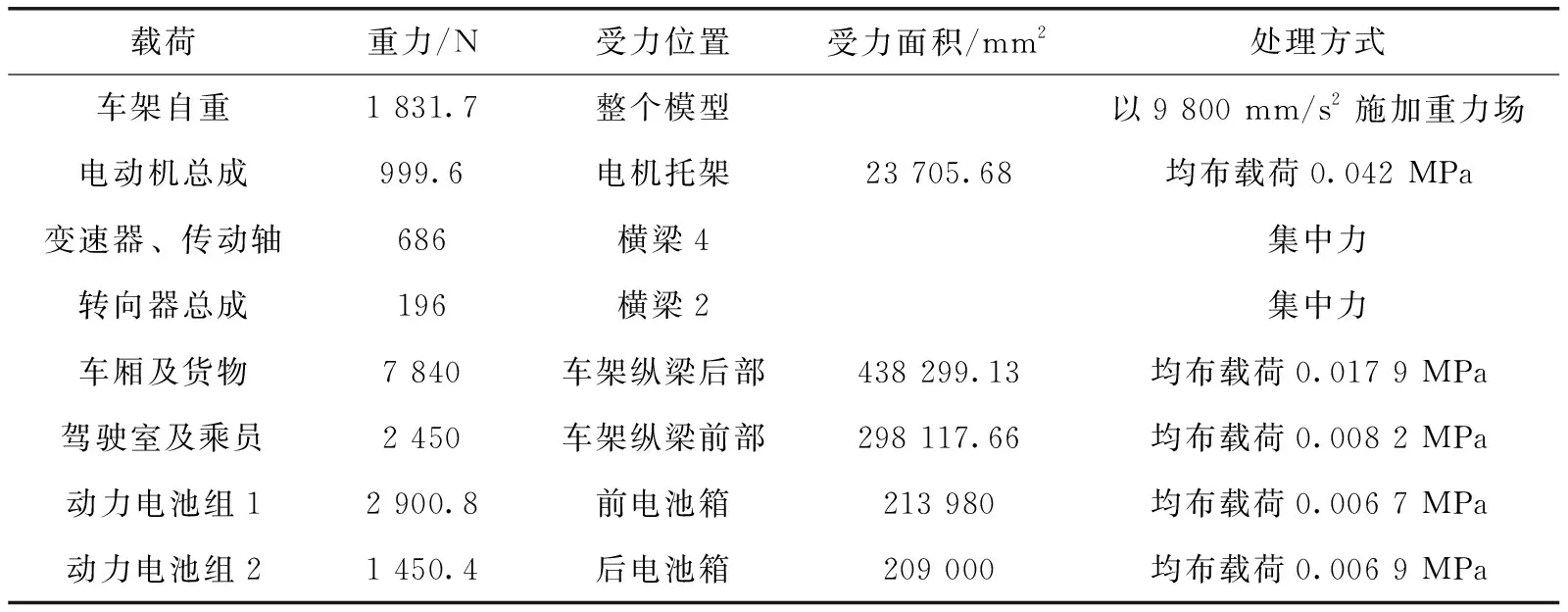
2.3 車架強度分析


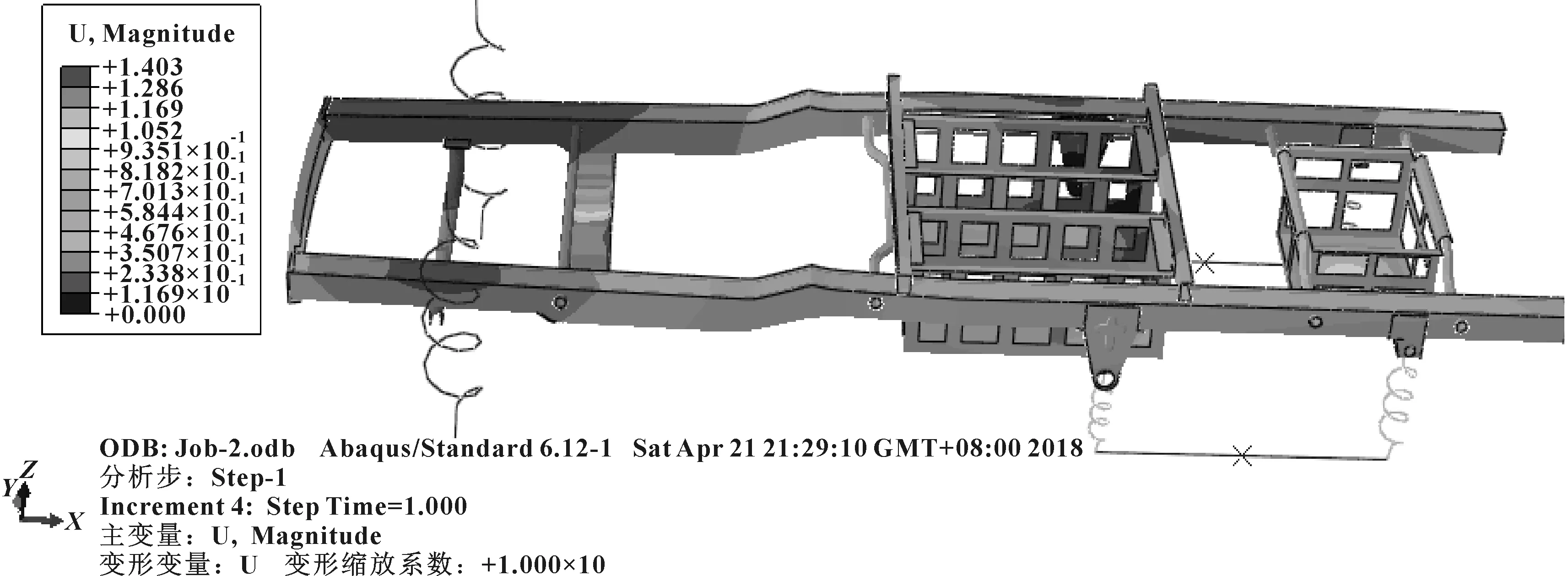
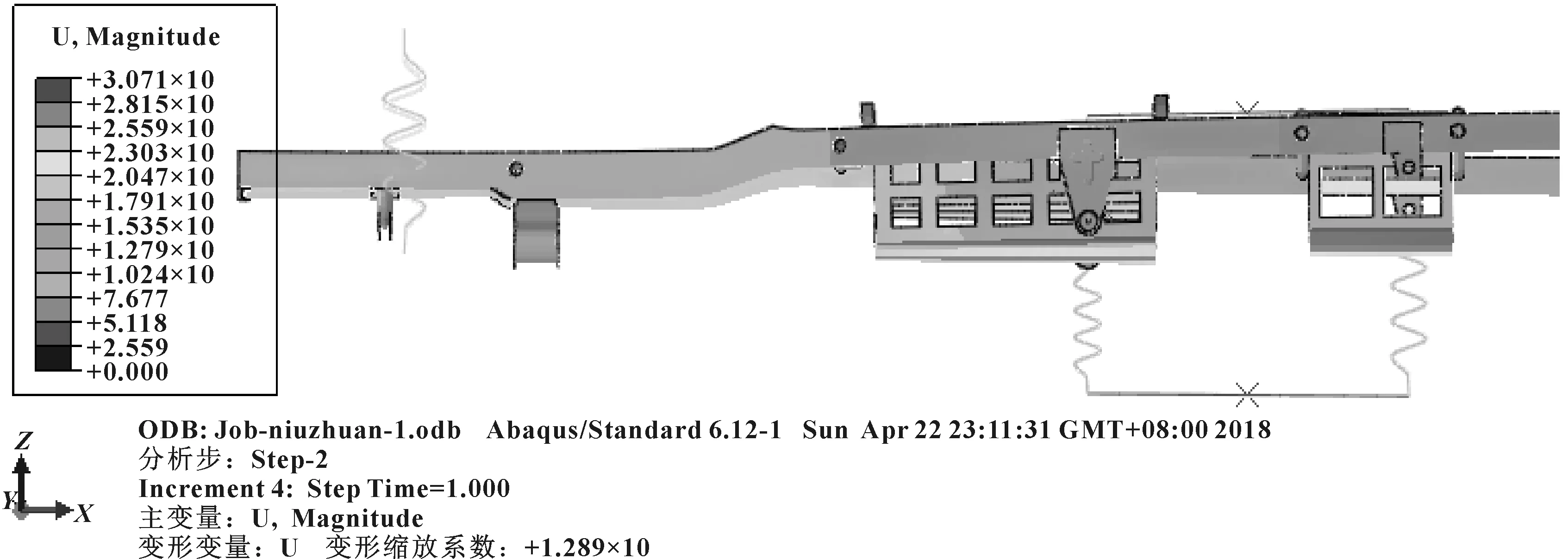

2.4 車架剛度分析
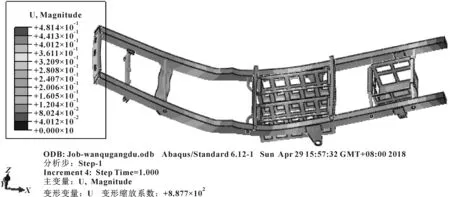
3 車架動態特性分析
3.1 車架模態分析
3.2 車架諧響應分析
4 結論

