基于MCMC的OFDM系統脈沖噪聲檢測與抑制方法

李冬霞, 劉國慶, 劉海濤

(中國民航大學智能信號與圖像處理天津市重點實驗室, 天津 300300)

0 引 言

正交頻分復用(orthogonal frequency division multiplexing,OFDM)是一種多載波數字調制技術,它以適合多徑信道傳輸、頻譜效率高、調制解調實現方便等優點,廣泛應用于無線通信系統和電力線通信系統[1-3]中。但是在實際應用中,會不同程度受到外界脈沖噪聲的影響,如汽車點火系統、大電流開關、高壓電力線或其他人為噪聲會嚴重影響接收信號的判決,給信號的有效傳輸和處理帶來極大的挑戰,造成系統性能下降[3-4]。因此，如何消除脈沖噪聲的影響成為OFDM系統應用的關鍵技術之一。

目前，在消除OFDM系統脈沖噪聲干擾的研究中所使用的方法主要分為參數法和非參數法。參數法主要是通過對接收信號進行限幅、消隱以及聯合限幅與消隱等非線性處理[4-5]消除脈沖噪聲的影響。脈沖限幅方法是通過設置限幅門限,對幅值大于該門限的接收信號取門限值,小于該門限的接收信號保留原幅值。脈沖消隱方法是設定峰值門限,將大于該峰值門限的接收信號作置零處理。仿真結果表明[4],脈沖限幅方法略優于消隱方法。以上參數法可有效抑制脈沖噪聲,提高系統性能,但是存在最優限幅門限設置困難以及產生子載波間干擾兩個主要問題。為確定最優限幅門限,文獻[6]提出基于最小誤比特率的自適應限幅門限設置方法,文獻[7]通過在時域和頻域計算接收信號幅值,選擇合適的門限值估計脈沖噪聲的起始位置,進而恢復信號,但是文獻[6-7]所采用方法需要知道噪聲的先驗知識,當噪聲模型和功率系數估計存在偏差時,無法得到最優門限,會導致系統整體性能惡化。為了解決由消隱產生的子載波間干擾問題,文獻[8]提出了一種迭代干擾消除方法,但該方法收斂速度較慢。非參數法主要是將時域脈沖噪聲信號建模為稀疏向量,利用稀疏重構技術構造出脈沖噪聲信號,直接將其從接收信號中分離。文獻[9]利用壓縮感知方法,從空子載波中估計出脈沖噪聲信號;文獻[10]提出了多模式壓縮感知方法,根據當前脈沖噪聲數量,自適應地改變用于重構脈沖噪聲的空子載波數量,有效降低脈沖噪聲的影響。但是文獻[9-10]所提壓縮感知方法需要滿足以下約束條件:在一個OFDM符號內的脈沖信號數量不能超過傅里葉變換點數和空子載波數目的最低門限值,由于脈沖噪聲信號本身具有隨機性,上述約束條件限制了該方法的使用。文獻[11]基于稀疏貝葉斯學習方法,根據決策回歸檢測,重構脈沖噪聲信號進而消除,但是在重構脈沖噪聲信號時需要知曉脈沖噪聲與高斯噪聲的狀態信息,并且計算復雜度較高,在實際系統中難以應用。

針對脈沖噪聲影響OFDM系統鏈路可靠性的問題,本文提出基于馬爾可夫蒙特卡羅(Markov chain Monte Carlo,MCMC)的turbo迭代均衡檢測方法。首先給出了OFDM系統發射機與接收機模型,在此基礎上根據MCMC方法原理,理論分析給出信道沖激響應、噪聲方差和頻域發送信號的條件分布,最后通過隨機樣本抽取和turbo迭代獲得未知量的參數估計,實現接收信號的解調。論文構建OFDM仿真系統,仿真給出了信道沖激響應和噪聲方差的估計曲線以及在加性高斯白噪聲(additive white Gaussian noise,AWGN)信道和多徑信道下系統的比特差錯性能曲線,證明OFDM系統存在脈沖噪聲時,本文方法比傳統信道估計方法精度更高,而且可以在未知脈沖噪聲先驗知識的情況下,比一般限幅處理方法獲得更有效的系統可靠性,在達到相同系統可靠性的條件下,比壓縮感知方法的傳輸效率更高。

1 系統模型

1.1 發射機模型

圖1給出了OFDM系統的發射機模型。系統發送相互獨立的二進制比特序列c,經過編碼速率為R的信道編碼器,得到編碼比特序列b,再經交織器后得到交織比特序列d,將d進行調制后得到頻域發送信號X,而后經離散傅里葉逆變換(inverse discrete Fourier transform, IDFT)到N路正交子載波上,得到時域發送信號x,最后添加循環前綴(cyclic prefix,CP),經D/A轉換器轉換為模擬信號發送到信道中。

圖1 OFDM系統發射機模型Fig.1 Transmitter model of OFDM system

1.2 接收機模型

圖2給出了OFDM系統接收機模型。接收模擬信號經過A/D轉換器轉換為數字信號,再去除CP,得到單個時域OFDM信號[10],表示為

y=x?h+v

(1)

式中,y=[y0,…,yN-1]T表示時域接收信號矢量,N表示子載波的數量;x=[x0,…,xN-1]T表示時域發送信號矢量;?表示卷積運算符號;h=[h0,…,hL-1]T表示信道沖激響應矢量;L表示多徑信道長度;v=[v0,…,vN-1]T表示時域干擾信號矢量,包括脈沖噪聲和高斯白噪聲。

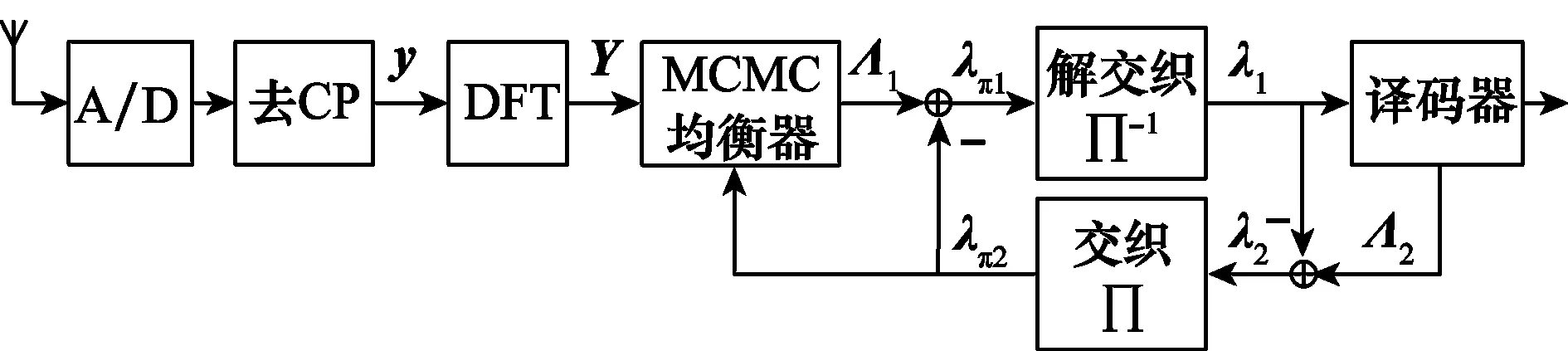
圖2 OFDM系統接收機模型Fig.2 Receiver model of OFDM system

vn服從伯努利高斯二項分布[12],表示為

(2)

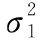
(3)

對式(1)進行N點DFT變換,得到頻域接收信號矢量Y,表示為

Y=HX+V

(4)

式中,H表示N×N信道頻率響應矩陣,其對角線元素表示為

(5)

X=[X0,X1,…,XN-1]T表示頻域發送信號矢量;V=[V0,V1,…,VN-1]T表示時域干擾信號矢量的傅里葉變換。式(4)進一步表示為

Y=DWLh+V

(6)

矩陣D是由X構成的對角陣,WL表示N×L點傅里葉變換矩陣為

(7)

圖2中頻域接收信號矢量Y送入到MCMC均衡器,并結合交織比特序列d的先驗對數似然比(log-likelihood ratio,LLR)信息λπ2(當無先驗信息時,λπ2=0)進行信道參數估計和頻域發送信號的檢測,計算關于交織比特序列d的后驗LLR信息Λ1。進一步通過式(8)給出由MCMC均衡器輸出交織比特序列d的LLR外信息λπ1,表示為

λπ1=Λ1-λπ2

(8)

式中，λπ1經過解交織器后得到編碼比特序列b的先驗LLR信息λ1。λ1一方面輸入到譯碼器計算編碼比特序列b的后驗LLR信息Λ2,另一方面與后驗LLR信息Λ2比較后,得到編碼比特序列b的LLR外信息λ2,表示為

λ2=Λ2-λ1

(9)

λ2經過交織器后得到先驗信息λπ2,輸入到MCMC均衡器中參與下一次迭代均衡,具體實現原理見本文第2.4節。

2 迭代均衡檢測原理

本節首先分析干擾信號模型,然后給出未知量的先驗分布,以及在頻域接收信號Y已知情況下的條件分布,最后介紹turbo結構中LLR信息的計算方法。

2.1 干擾信號頻域分析

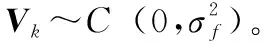
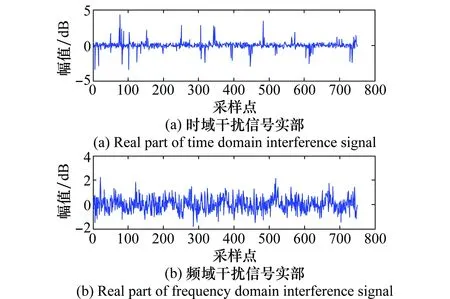
圖3 干擾信號時頻對比圖Fig.3 Time-frequency comparison of interference signal

2.2 先驗分布

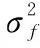
(1)信道沖激響應矢量服從復高斯分布,表示為

p(h)～CN(h0,Σ0)

(10)

式中,h0表示均值矢量;Σ0=εIL表示協方差矩陣,ε可選取任意一個比較大的值,IL表示L維單位矩陣。

～χ-2(2α,β)

(11)

或者可以表示為

(12)

式中,α表示逆卡方分布的自由度;β表示累積概率;Γ(·)表示Gamma函數。

(3)第k個子載波對應頻域發送信號為aj的先驗概率表示為

ρk,jP(Xk=aj)

(13)

式中,aj∈A,A表示MPSK的星座集合。ρk,j可以通過譯碼器端反饋的先驗LLR信息λπ2計算得到(具體計算方法見第2.4節)。在未知頻域發送信號矢量先驗信息的情況下,ρk,j=1/|A|。

2.3 條件分布

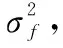
(14)

其中

(15)

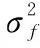
(16)

其中

(17)

(18)

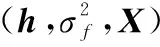
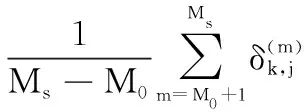
(19)

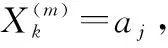
信道沖激響應和頻域干擾信號方差的估計值可以根據MCMC均衡器抽樣樣本均值計算得到,表示為

(20)

(21)

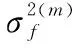
(22)

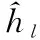
2.4 turbo迭代譯碼

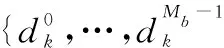
(23)

即可以根據MCMC均衡器得到的頻域發送信號的后驗概率進行計算。由貝葉斯準則,式(23)可分解為兩部分,即

(24)

(25)

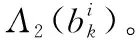
根據式(24)第二項,交織比特為“0”或“1”的概率可以通過式(26)計算得到。

(26)

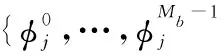
(27)

該先驗概率送入MCMC均衡器中根據式(14)、式(16)、式(18)進行下一次信道沖激響應、干擾噪聲方差和頻域發送信號的抽樣,經過幾次迭代后,譯碼器輸出結果會越來越準確。

3 數據仿真結果

3.1 仿真參數設置

為驗證本文基于MCMC的turbo迭代均衡檢測方法的有效性,設計OFDM仿真系統,仿真參數設置如下:信道編碼采用碼率為1/2的[7,5]卷積編碼,調制方式采用BPSK,子載波數量為256,循環前綴的長度為44,多徑信道長度為4,譯碼方式為軟判決維特比譯碼,信干比設置為-7 dB,脈沖噪聲發生的概率ρe=0.1。在MCMC均衡器中,進行未知量初始化時,參量初始值設為:(α,β)=(1,0.1),h0=0,ε=1 000。抽樣次數Ms=100,預燒期M0=50。

MCMC方法屬于盲檢測算法,在信號的盲估計過程中容易出現相位模糊問題[16]。為此,本文在MCMC均衡器進行抽樣之前,利用導頻對信道沖激響應矢量進行初始估計[17],然后采用迫零檢測,獲得初始頻域發送信號。在MCMC均衡器抽樣過程中,由于抽樣樣本隨機產生,會出現均衡器無法達到收斂狀態,因此,根據初始信道估計,確定信道沖激響應|hl|,l=0,1,…,L-1最大時對應的信道下標lmax,當MCMC均衡器進行M0次抽樣后,如果信道沖激響應抽樣樣本對應的最大信道下標lsample=lmax,則繼續抽樣,否則重新進行抽樣。

3.2 仿真結果

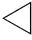
仿真曲線觀測表明:①在AWGN信道下本文方法可以提高系統的性能;②隨著迭代次數的增加,系統性能改善越明顯,與無脈沖干擾情況下有近2 dB的差距;③本文方法的性能明顯優于脈沖限幅方法;④空子載波數64時,本文方法的性能明顯優于壓縮感知方法,空子載波數128時,本文方法與壓縮感知方法性能趨于一致。

圖5和圖6分別給出了在多徑信道下,SNR為9 dB,MCMC均衡器收斂后得到的信道沖激響應矢量和頻域干擾信號方差抽樣曲線,其中橫坐標表示抽樣次數,縱坐標表示參數值。圖5中實線表示MCMC均衡器抽樣得到的信道沖激響應矢量實部的抽樣值,虛線表示虛部的抽樣值,點線表示理想情況下的實部值,點橫線表示理想情況下的虛部值。圖6中實線表示頻域干擾信號方差的抽樣值,虛線表示理想情況下的值。仿真曲線觀測表明:①在抽樣次數較少時,信道沖激響應和干擾噪聲方差的抽樣值存在較大波動;②隨著MCMC均衡器逐漸達到收斂狀態,抽樣值非常接近于真值。

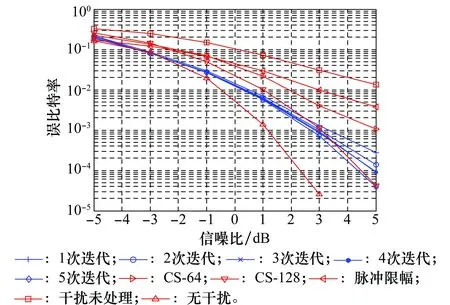
圖4 比特差錯性能曲線(AWGN信道)Fig.4 BER performance (AWGN channel)

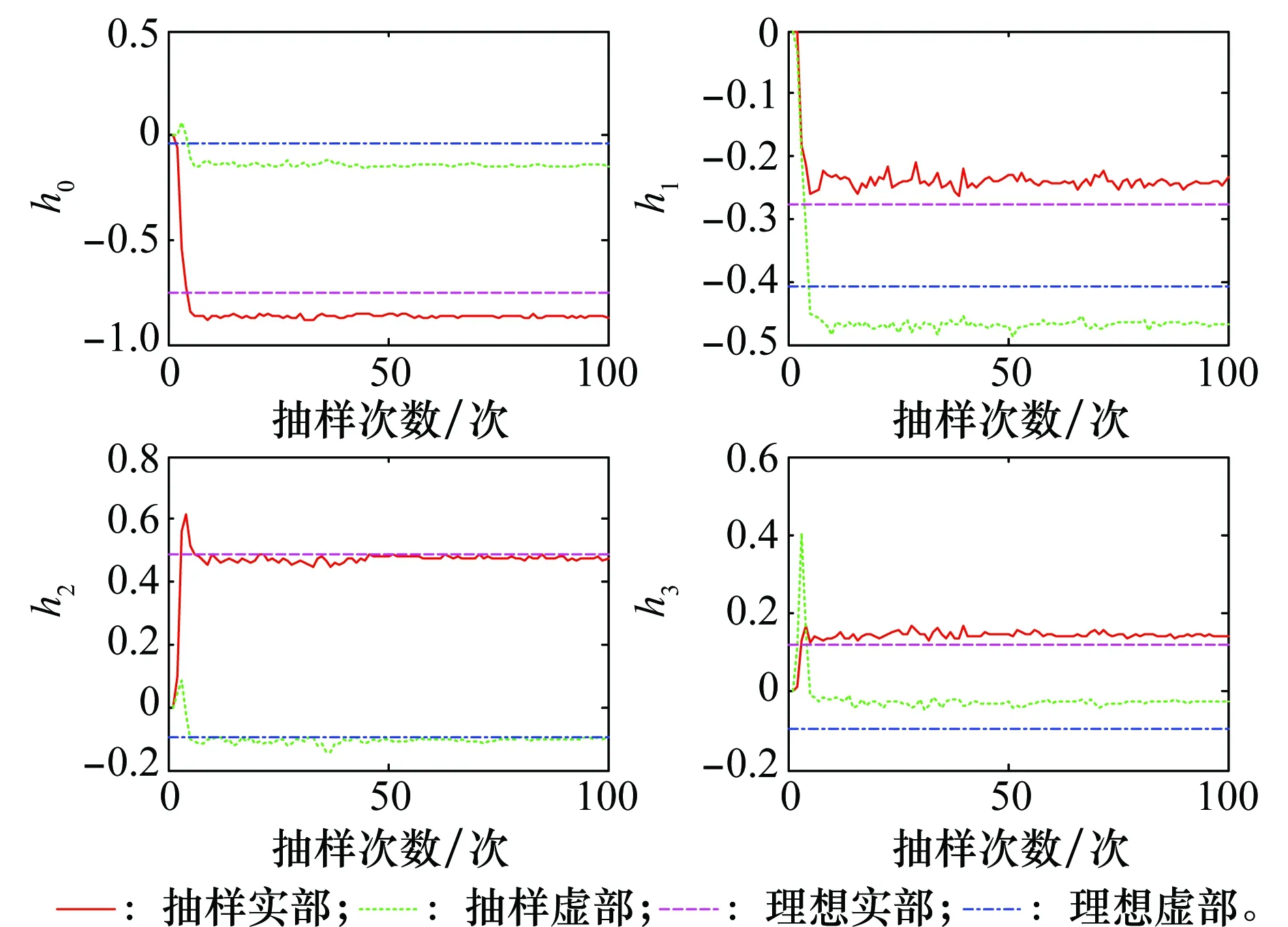
圖5 信道沖激響應抽樣曲線(多徑信道,SNR=9 dB)Fig.5 Samples of channel impulse response (multipathchannel, SNR=9 dB)

圖7顯示給出了在多徑信道下,SNR為-3～12 dB,信干比為-7 dB,根據式(22)計算得到的信道沖激響應的MSE曲線。圖中標注“□”的紅色曲線表示在相同條件下采用最小二乘(least squares, LS)方法估計得到的信道沖激響應的MSE曲線,標注“+”“○”“×”“●”“◇”的藍色曲線分別表示本文方法經過turbo迭代1～5次后得到的MSE曲線。仿真曲線觀測表明:①本文方法比傳統的LS信道估計方法精度更高;②隨著迭代次數的增加信道估計更為精確。

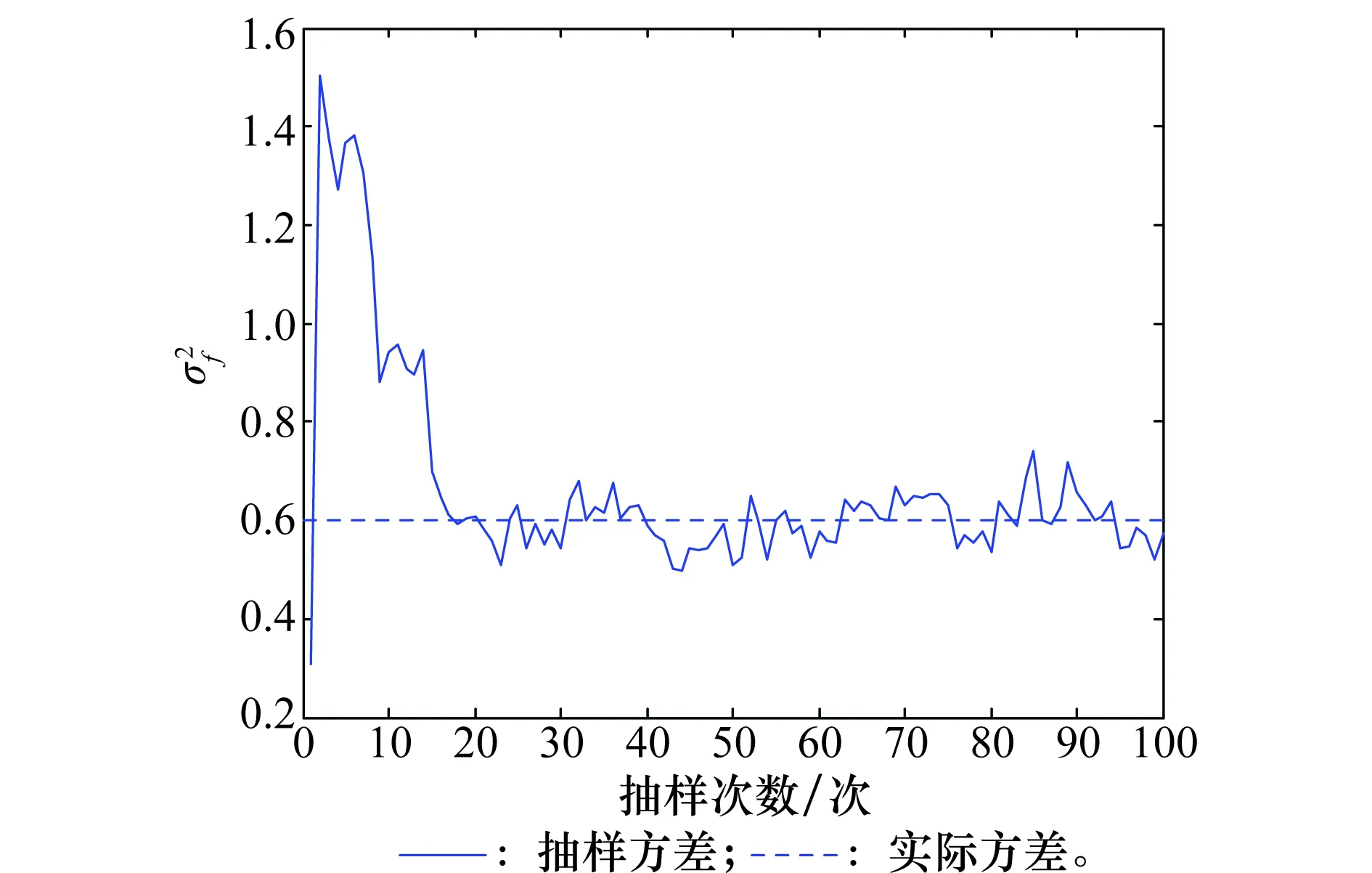
圖6 頻域干擾信號方差抽樣曲線(多徑信道,SNR=9 dB)Fig.6 Variance samples of frequency domain interference signal(multipath channel, SNR=9 dB)

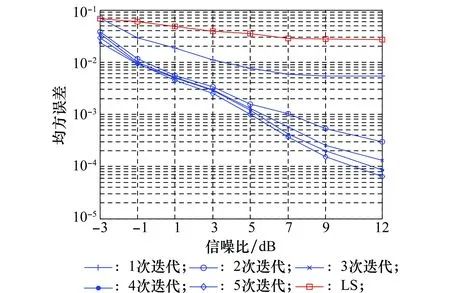
圖7 信道沖激響應的均方誤差曲線(多徑信道)Fig.7 Mean square error of channel impulse response(multipath channel)

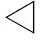
仿真曲線觀測表明:①在多徑信道下本文方法可以提高系統的可靠性;②隨著迭代次數的增加,系統可靠性改善越明顯,當誤比特率降到10-4以下時,與無脈沖干擾情況下有近3 dB的差距;③本文方法的性能明顯優于脈沖限幅方法;④空子載波數64時,本文方法的性能明顯優于壓縮感知方法,空子載波數128時,本文方法與壓縮感知方法性能相差不大。

圖8 比特差錯性能曲線(多徑信道)Fig.8 BER performance (multipath channel)

4 結 論

針對OFDM系統中存在脈沖噪聲,從而影響系統鏈路可靠性的問題,提出基于MCMC的 turbo迭代均衡檢測方法。研究結論如下:①基于MCMC的turbo迭代均衡檢測方法可以利用已知接收信號與未知量的相互聯系,在噪聲先驗信息未知的情況下,得到信道沖激響應和干擾信號方差的估計值,同時實現信號檢測;②通過比較信道估計的MSE曲線,該方法中比傳統LS信道估計方法精度更高;③與一般限幅方法相比,本文方法可以更加有效地提高系統可靠性,在達到相同系統可靠性的條件下,比壓縮感知方法的傳輸效率更高。