某機床伺服電機懸置剛度區間型穩健優化方法研究
王 營,吳進軍,錢 蒙,張利強
(機械科學研究總院集團有限公司 中機生產力促進中心,北京 100044)
0 引言
目前,傳統的確定性優化方法(即假定變量的優化值可以被無偏差的實現)已經廣泛應用于伺服電機和動力總成懸置的剛度、位置等參數的優化[1,2]。但是,在懸置的制造、安裝和使用過程中,剛度及位置的實際值與其優化值必然存在一定程度的偏差(稱之為不確定性),從而造成懸置系統的固有頻率和解耦率等性能指標也與預期的優化值不同。因此,在懸置參數優化階段準確預測懸置系統固有頻率和解耦率的變化特征有重要的理論和工程實際意義。
研究不確定性問題主要有三種方法:概率方法、模糊方法和區間方法[3]。概率方法需要獲取不確定參數的概率密度函數等統計信息,模糊方法也需要知道模糊參數的隸屬度函數,它們的獲取,一般需要通過大量試驗或經驗,成本較高,精度卻不高。區間方法是最近幾十年才出現的數學上的一個新興分支,其優勢是只需要不確定參數的上、下界限,因此更容易被應用。
Sirafi和Chang[4]研究了懸置剛度的波動對某懸置系統解耦率的影響。Qatu[5]分析了懸置剛度的變化對懸置系統固有頻率的影響。Jiang等[6]把結構載荷、彈性模量或泊松比當作區間參數,提出了一種區間規劃方法。吳杰等[7]把懸置剛度看作隨機參數和區間參數,對懸置系統進行了優化研究,結果表明二者一致性較好。
文中采用區間數表征設計變量的不確定性,給出區間型穩健優化方法對某機床伺服電機懸置剛度進行穩健優化,其中考慮了剛度設計值的偏差對系統性能指標的影響,并對優化結果進行穩健性分析,驗證穩健優化方法的有效性。
1 穩健性優化和分析原理
圖1是確定性優化和穩健優化的原理圖[7]。確定性優化的解通常位于約束條件的邊界,當由于誤差而發生波動時,優化方案的實際值可能進入不可行域而使優化失效。因此,確定性優化方法雖然獲得了優化方案,卻不能確保方案的穩健性。
穩健優化方法不僅要優化目標函數,還要降低目標函數和約束條件對設計變量的靈敏度。優化方案的穩健性可以用約束條件的滿足程度和目標函數對設計變量的靈敏度大小來衡量。
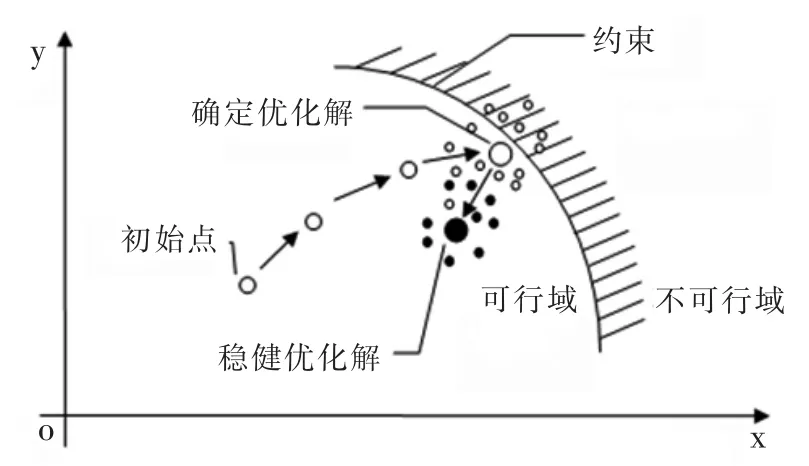
圖1 確定性優化和穩健優化的原理Fig.1 Principle of deterministic optimization and robust optimization
若設計變量為正態分布隨機變量,則優化方案的穩健性可以用目標函數及約束條件的σ水平(σ為標準差)來衡量。每個σ水平對應的正態分布曲線下的面積,正是目標函數值或約束條件值落在其中的概率 (或稱為可靠度)[8]。表1中給出了不同σ水平對應的概率(或可靠度)及每百萬產品的次品個數(DPM)。
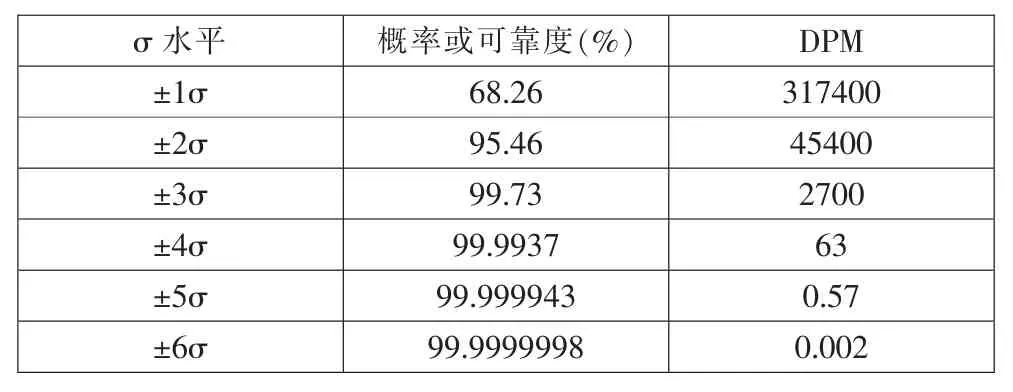
表1 不同水平對應的概率和每百萬產品的次品個數Tab.1 Relation between level and probability or DPM
2 懸置系統的區間型穩健優化模型
受到伺服電機布置空間的限制,不對懸置的安裝位置和安裝角度進行優化,故只優化懸置剛度。因此,確定性優化模型可表示為:

其中,fi—第i個自由度方向的固有頻率;di—對應于頻率fi的解耦率;wi—權重;fiL和fiU分別為fi的下、上界限,diL為 di的下界;kj—第 j個剛度設計變量,kjL和 kjU分別為kj的下、上界;l為設計變量個數。
考慮到懸置剛度的實際值與優化值之間的偏差,為使懸置系統頻率和解耦率的優化值更加穩健,在優化時,應考慮到剛度名義值的波動對優化結果產生的影響。因此,區間型穩健優化模型不但要提高懸置系統的解耦率,當懸置剛度在其名義值附近波動時,還要保證解耦率和固有頻率等系統性能的變化區間半徑最小,即穩健性最好。
因此,懸置系統區間型穩健優化模型為:

其中,kj—懸置剛度名義值;kjL和kjU分別為下界和上界;kjI=[kj-δ,kj+δ]—懸置剛度值在其名義值附近的波動區間;δ—波動幅度;fiI=fi(k1I,k2I,…klI)和 diI=di(k1I,k2I,…klI)分別是懸置剛度值在其名義值附件波動時,懸置系統各階固有頻率和解耦率的變化區間;mid(diI)和 rad(diI)分別為各解耦率變化區間的中點值和半徑[9],α、β為比例系數,wi、vi為權重。
式(2)的約束條件中含有區間數之間的序關系(即大小關系)問題,文獻[6]給出了區間數序關系的一種量化方法,即區間可靠度,其表達式為:
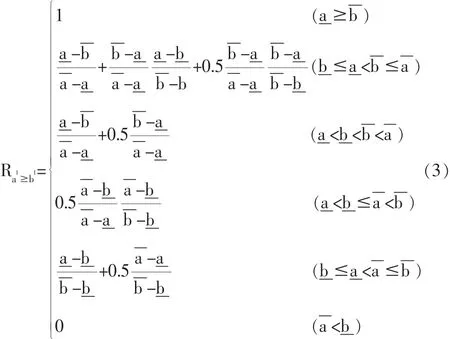
由式(3)中的區間可靠度定義,可以將穩健性優化的區間型約束條件轉換為可靠度約束條件。例如,區間型約束條件為fiL≤fiI≤fiU,寫成可靠度約束條件為且和分別為滿足約束條件i的左、右區間可靠度。因此,式(2)可以轉化為式(4)所示的穩健性優化模型:
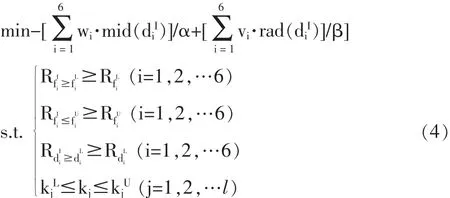
3 解耦率及頻率的變化區間
穩健優化模型中需要計算解耦率及頻率的變化區間,當懸置剛度在其名義值附近波動時,通過靈敏度分析可知,懸置系統的固有頻率和各方向解耦率均為各懸置剛度值的單調函數。因此,可以采用組合方法求得固有頻率和解耦率的精確區間值[9]。
當區間變量取端點值時,f(k1I,k2I,…knI)的所有可能取值為:
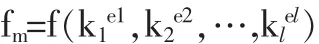
其中,ej=L,U,j=1,2,…,l,m=1,2,…2l。
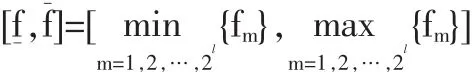
4 算例
圖2為某機床伺服電機懸置系統(SMMS),電機坐標系G0-XYZ的原點G0位于電機質心,X軸與電機軸同向,Z軸垂直曲軸向上,Y軸由右手法則確定。將懸置簡化成沿其三個彈性主軸方向具有剛度和阻尼的元件[1],橡膠懸置阻尼很小,可忽略阻尼。以懸置的3個彈性主軸方向建立懸置局部坐標系(LCS)oi-uiviwi,懸置的三個彈性主軸分別用 ui,vi和 wi表示(i=1,2,…,n,n 為懸置個數)。
6個固有頻率的約束范圍分別為5~30Hz,要求Z軸和Roll方向的解耦率高于90%,其它方向的解耦率高于80%。假設kj可以在其初值kj附近變化±30%。
4個懸置的初始剛度值及優化剛度值見表2。
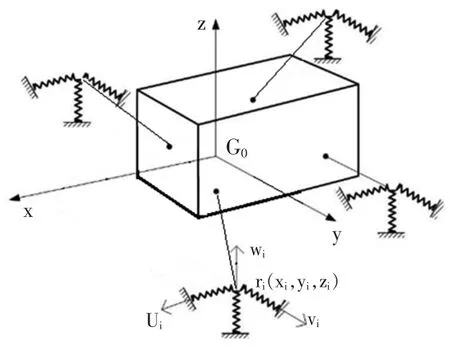
圖2 電機懸置系統示意圖Fig.2 Simplified model of the SMMS
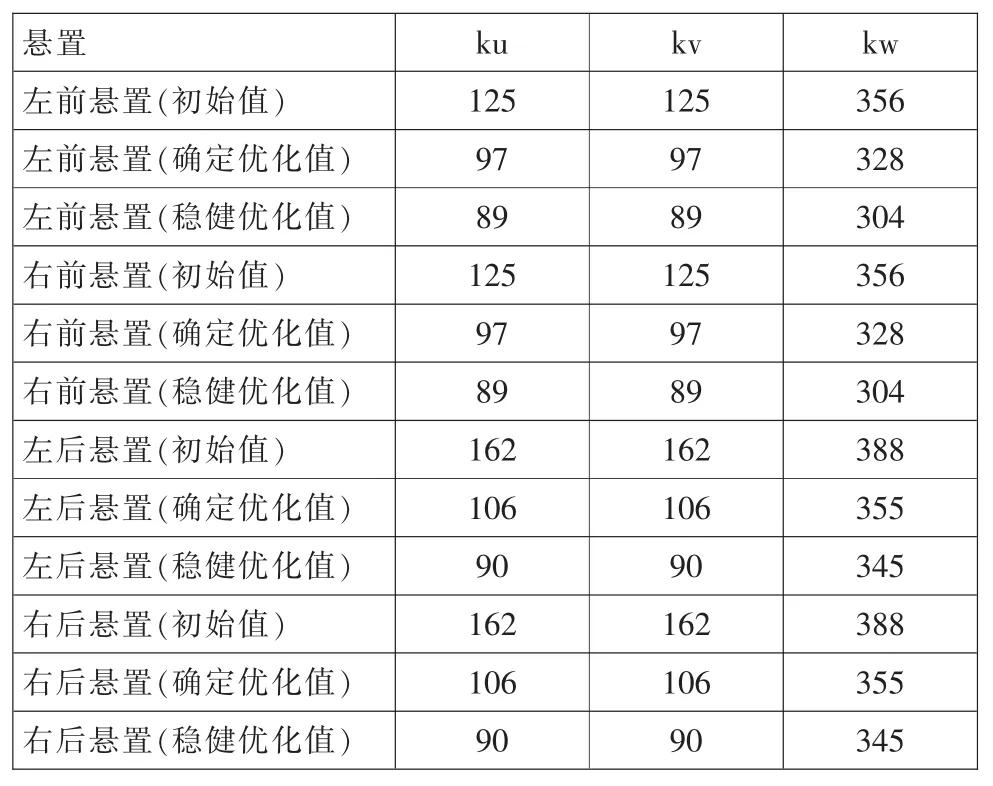
表2 懸置初始及優化靜剛度(N/mm)Tab.2 Original and optimized static stiffness of the mounts(N/mm)
表3給出了懸置系統初始方案在各方向的頻率和解耦率,解耦率的計算方法詳見文獻[1]。由表3可知,除Y方向以外,該懸置系統的解耦率普遍較低,意味著各方向的耦合振動較嚴重。

表3 懸置系統固有頻率和解耦率的初始值Tab.3 Origin frequency and decoupling ratio of the SMMS
假設式(4)中所有頻率約束條件的左、右區間可靠度均要求為1.0。優化結束后,表4給出了當確定性優化和區間優化所得到剛度優化值波動時,解耦率的變化區間。一般地,懸置剛度值的波動δ幅度約為10%~15%,文中對波動幅度為10%和15%兩種情況進行討論。
從表4可知,區間優化和確定性優化均可提高懸置系統的解耦率。由于在穩健優化模型中考慮了解耦率的穩健性要求以及設定頻率約束條件的區間可靠度為1.0,所以導致解耦率稍有降低。由表4可以看出,波動幅度δ增大時,解耦率的區間半徑增大,即不確定性增大。
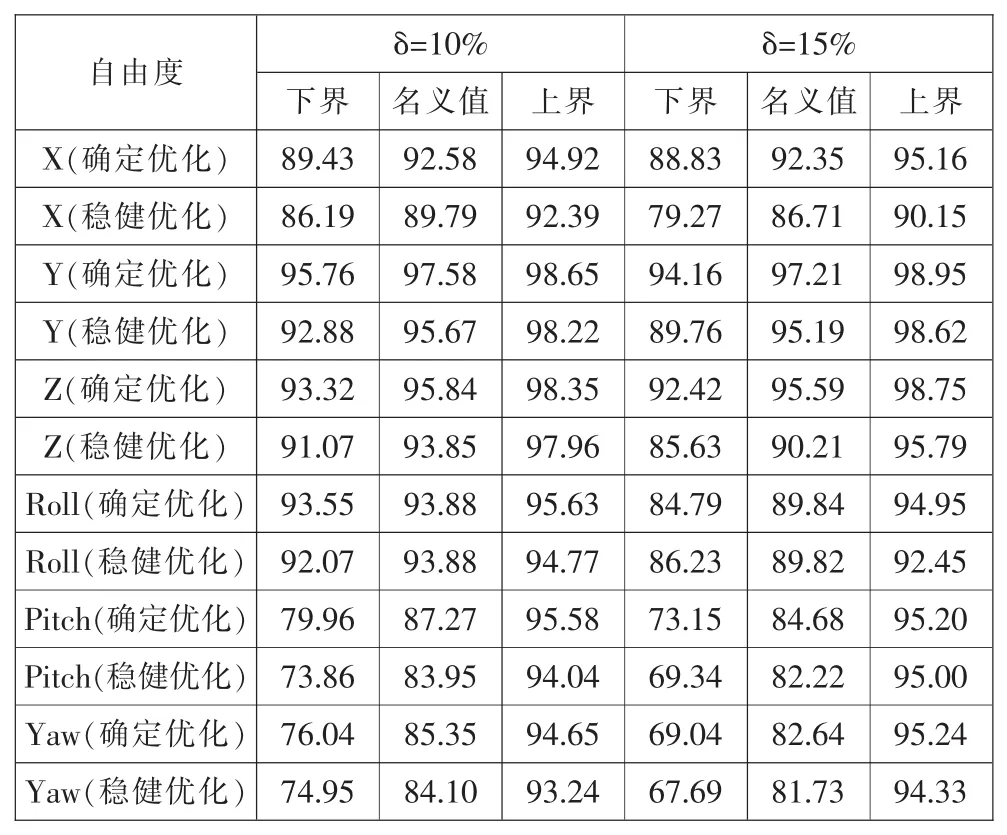
表4 優化后懸置系統解耦率的變化范圍(%)Tab.4 Intervals of the optimized decoupling ratios(%)
表5給出了當確定性優化和區間優化所得到剛度優化值波動時,頻率的變化范圍,以及在確定性優化和穩健優化的剛度名義值處各約束條件的左、右區間可靠度。可以看出,波動幅度δ增大時,頻率的區間半徑增大,即不確定性增大。將懸置剛度值看作正態分布的隨機變量,對優化結果進行σ水平分析,可以看出,頻率約束的左右區間可靠度越大,σ水平越高,穩健性越好,反之越低。

表5 優化后懸置系統頻率變化范圍及頻率約束的左右區間可靠度和水平Tab.5 Intervals of the optimized decoupling ratios and the interval reliability degrees and levels of the optimized SMMS
當穩健優化得到的剛度優化值有所波動時,各約束條件左、右區間可靠度較確定性優化有較明顯增大,表明頻率約束的穩健性有較大幅度的提高,在Z和Roll方向尤為明顯,相應地,σ水平也有明顯提高。這表明,文中給出的表征頻率穩健性的度量指標是合理的,穩健優化結果是有效的。
5 結束語
提出的區間型穩健優化方法不僅能有效提高懸置系統各方向的解耦率,與確定性優化方法相比,穩健優化方法還可以較大幅度地提高頻率和解耦率的穩健性。
穩健優化方法在優化過程中考慮到設計變量的波動對優化結果的影響,在不易獲得或很難精確獲得不確定參數的統計特性或模糊信息的情況下,采用該方法可以有效提升懸置系統性能的穩健性。

