基于加權拉格朗日二次插值的直線電機誤差補償方法

王 征，袁清珂 ，蕭 顯，肖 聰

（廣東工業大學 機電工程學院，廣東 廣州 510006）

0 引言

近年來，隨著高速切削、精密加工等先進技術的發展，精密制造加工行業開始推行高精度、快速響應的定位裝置[1]。直線電機作為一種典型的單軸傳動定位機構，具有結構簡單，無接觸運行，噪聲低，速度和精確度高等優點[2，3]。直線電機通常是在PMAC條件下，采用帶物理反饋的閉環控制方式進行加工定位，雖然目前的控制技術已經較為成熟，但是在實際的應用中，并不能完全消除非控制層面的影響。文獻[4]在低速運動條件下，研究了滑臺摩擦力對直線電機定位精度的影響，改進了補償控制器，降低了跟蹤誤差；文獻[5]提出了帶前饋的PID混合控制方法，并進行了振動誤差的補償實驗，為后續的研究提供了一定的技術支持；文獻[6，7]從直線電機驅動工作臺出發，分別對電機發熱和摩擦熱進行了特性分析，為熱量對機臺精度影響的研究提供一定的指導意義，但并未涉及如何消除該特性誤差方面；文獻[8]提出了采用誤差補償表進行補償，但本質是采用離散的補償模型，不能保證工作行程內的點位都具有可靠的定位精度。

本文從影響直線電機定位精度的因素出發，對電機控制方法進行分析和改進，并提出加權拉格朗日二次插值的補償方法，經過實驗分析證明了該方法的可行性，能夠補償外界物理因素造成的定位誤差。

1 直線電機定位精度影響因素分析

直線電機通常采用帶反饋的閉環控制方式，可以通過反饋裝置對動子的位置進行精確調整，但是在實際使用中可能存在光柵尺的裝配誤差、設備老化、機臺振動和高溫形變等影響因素，在諸多因素的綜合作用下會累積較大的隨機誤差。

激光干涉儀是能夠測量線性定位精度的設備，可精確到0.1μm，并且可以通過外部傳感器近似補償環境溫度、材料表面溫度、濕度和振動造成的誤差。圖1為激光干涉儀測量電機定位精度的對比曲線，其中直線電機有效測量行程為0mm～500mm，測量間隔為10mm，單點停頓時間為 5s，環境溫度為 24°C。

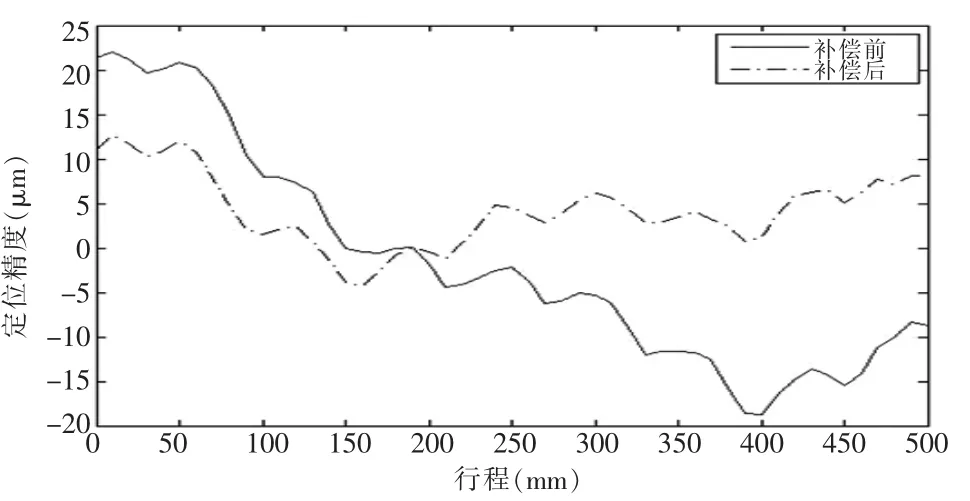
圖1 補償前后定位精度對比圖Fig.1 Comparison of positioning accuracy before and after compensation

由圖1可以看出，未開啟激光干涉儀補償功能時，所檢測的定位精度在±22μm以內，開啟補償后，定位精度在±13μm以內。該數據表明在直線導軌摩擦生熱、電機自身產熱、機臺振動等因素的綜合影響下，產生了較大的定位誤差，精密加工設備通常要求定位精度在±6μm之內，因此目前的情況不能滿足實際需求。

2 前饋-PID混合控制方法

針對多因素綜合影響問題，選擇采用前饋和PID混合控制的方法，根據干擾的作用量進行補償。被控變量所產生誤差是由干擾引起的，而干擾是諸多影響因素的綜合作用結果，若每個主要因素都設置一個前饋通道，將會大大增加使用和維護的成本，因此本文提出將干擾進行綜合和參數化處理，設置單個通道進行控制。

圖2為前饋-PID混合控制的系統框圖，該系統主要由基于插值法的前饋控制器、PID控制器、D/A和A/D轉換器、驅動器、直線電機以及光柵尺等組成。

圖2 前饋-PID混合控制的系統框圖Fig.2 Feed-forward PID hybrid control system block diagram

當工控機輸出移動指令時，將計算所得的理論位置坐標輸出給前饋控制器，前饋控制器通過內部運算輸出該點的補償控制信號，進行定位精度的“粗調”，用以補償外界物理干擾；另一方面，信號通過PID控制器處理，伺服驅動器發出脈沖信號控制直線電機的動作，同時通過光柵尺的反饋作用補償機械誤差。

3 加權拉格朗日二次插值數學模型

拉格朗日二次插值方法即在被插函數曲線上任取相鄰三個點作為插值節點，以這三個點作一條二次曲線來近似地表示原曲線。

加權拉格朗日插值多項式可以表示為[9]：

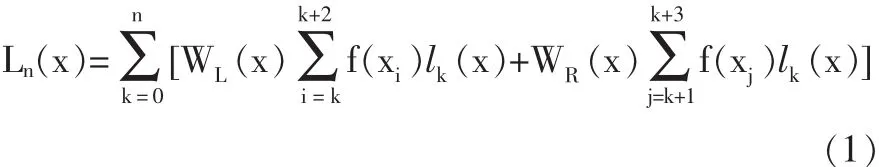
其中 lk（x）為拉格朗日插值基函數，WL（x），WR（x）為加權因子：

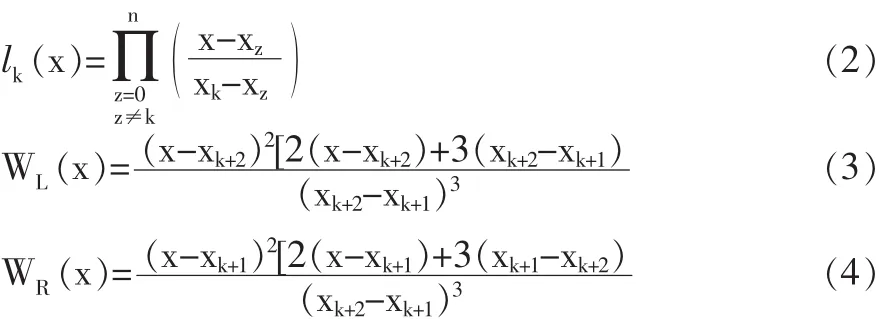
在任意相鄰兩節點間作插值，考慮到插值點左右兩側的插值節點不同，曲線的趨勢也不同，所以分別以左右兩側的插值節點作兩條不同的曲線，然后通過加權的方法將兩條曲線融合成一條插值曲線，從而獲取更加精準的定位信息。

例如在 x1，x2之間插入一點 xi， 則選取 x0，x1，x2和 x1，x2，x3分別構造一條插值曲線：

4 誤差補償余項分析

設函數 y=f（x）在區間[a，b]上有定義，并且存在 n+1個插值節點 xi（i=0，1，2…，n）。假設 f（x）在[a，b]上存在 n+1階導數，使用n階插值多項式pn對函數f（x）進行插值，則對于任一個 x∈[a，b]有：

其中：

選取均勻分布的插值節點，對任意的M>0均有maxx∈（a，b）｜f（n+1）（x）｜≤M，進而可得：

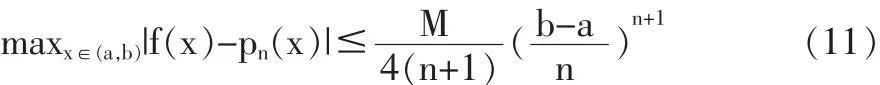
選取 n=2，即在 xi-1，xi，xi+1三點之間進行二次插值，插值點為 x∈（xi，xi+1），則插值函數為：

此處設定直線電機的行程為540mm，為了降低系統的復雜程度，提高方法的通用性，以10mm為采樣間距，在全量程采集55個定位點坐標作為補償樣本，設xi+1/2為xi，xi+1的中點，可以得出：

其中Ri+1/2為誤差補償余項，

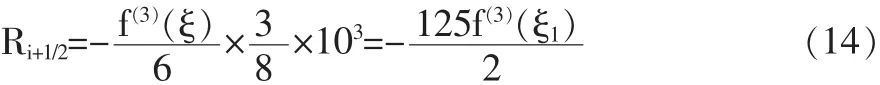
在插值過程中，考慮到轉折點的情況，因此需要對余項進行分析，定義在xi+1/2左右兩側的余項：

插值點xi的插值多項式為：

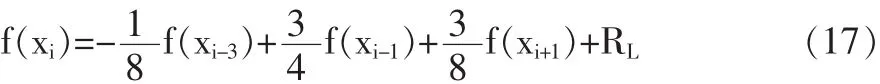
式中：

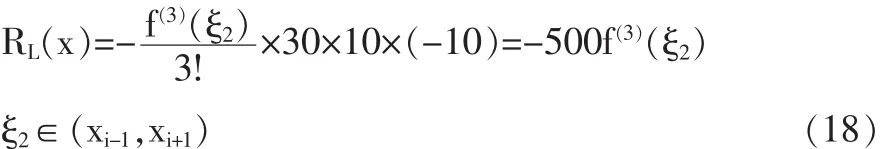
考慮到直線電機運動測試中，采樣點個數足夠多，且任意相鄰兩點之間的變化不大，因此通過對比（14）（18）式可以得到：

綜上所述，在直線電機工作行程內的加權拉格朗日二次插值補償公式為：

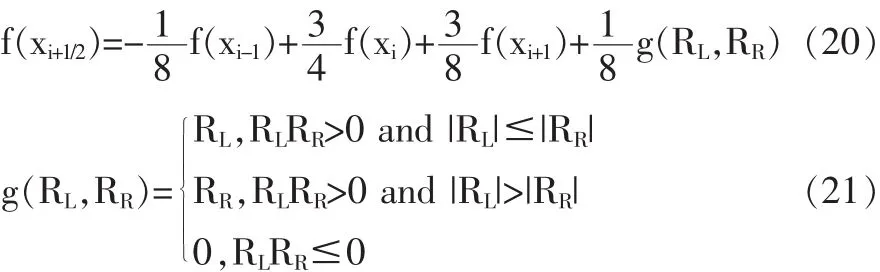
在數據點出現轉折和波動的情況時，g（RL，RR）可以確定誤差補償的方向[10]，若RL，RR異號，證明在插值子區間內存在轉折點的情況，若RL，RR同號，選取較小的值作為誤差補償參數，從而更加可靠地對直線電機的定位誤差進行補償，并且該方法具有自適應性。

5 實驗分析

誤差補償實驗平臺如圖3所示。實驗平臺主要包括減振大理石基座，直線電機模組，傳送平臺，運動控制卡及控制電路，工控機，激光干涉儀及其補償傳感器等。

設置直線電機的實驗行程為540mm，動子運動速度為100mm/s，環境溫度為24℃，在此條件下設計三組實驗記錄位置坐標和定位精度等數據，獲取補償效果評價圖像。

圖3 誤差補償實驗平臺Fig.3 Error compensation experiment platform

在直線電機未開啟補償功能時，需要先獲取若干參考點處的定位精度。本次實驗選擇了55個點位作為補償的樣本信息。將該樣本信息接入補償模塊后開啟使能，使用激光干涉儀測量該55個節點位置的定位精度，由圖4（a）可以看出補償后所有插值節點的定位誤差均在±1μm以內，具有很好的精確度。

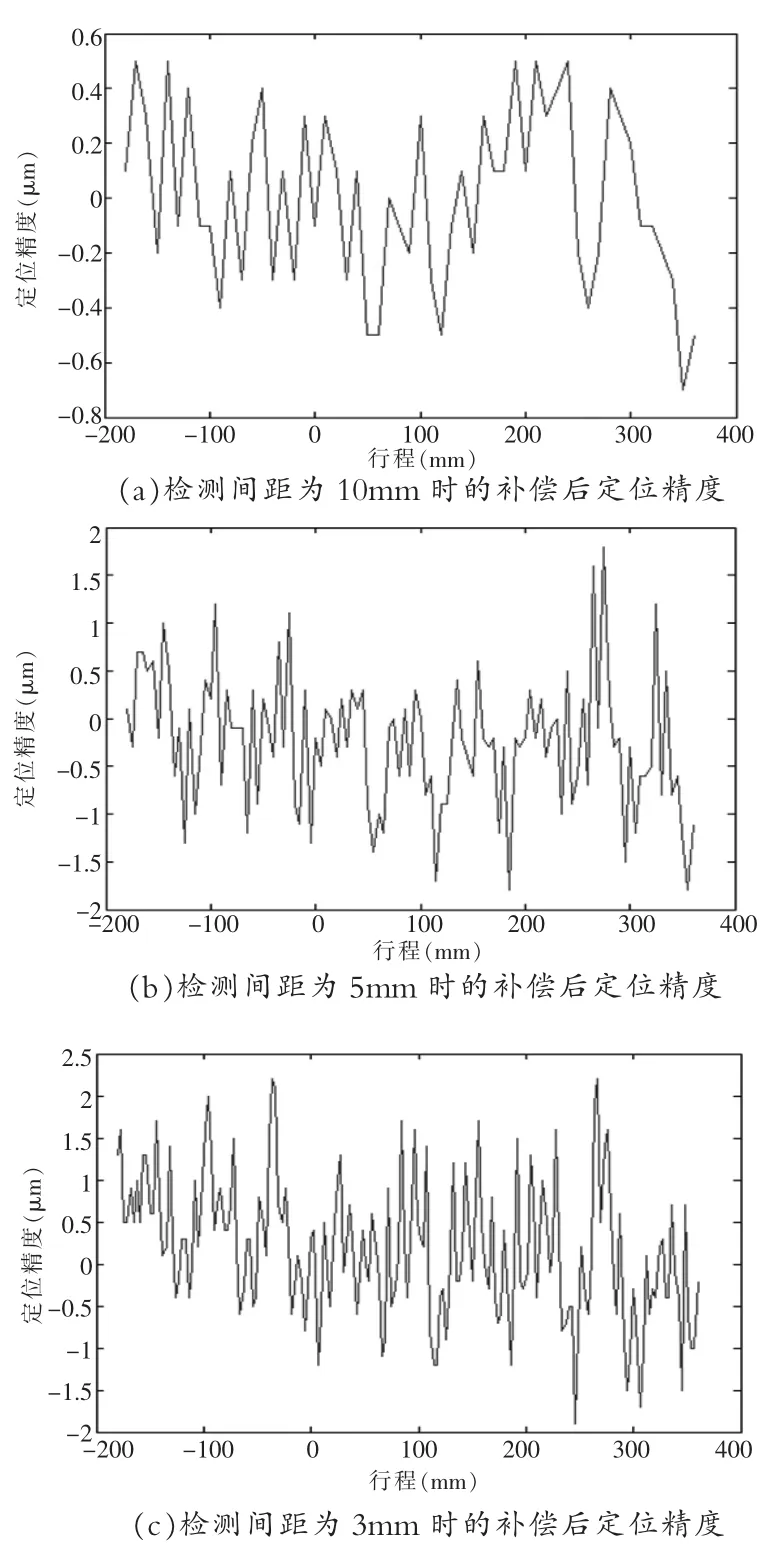
圖4 補償后定位精度圖Fig.4 Positioning accuracy after compensation

為了檢驗全程補償效果，將檢測點細化，圖4（b）是間距為5mm時檢測109個定位點的定位精度曲線，由圖像可以看出通過該方法所補償的全部點位基本穩定在±2μm范圍內，圖4（c）是間距為3mm時檢測181個點位的定位精度曲線，在此條件下規避了所有的對點補償和插值補償點位，由圖像可以看出整體定位精度穩定在±2μm范圍內，由于系統的隨機誤差產生了個別異常波動的情況，但是波動的峰值仍然在±2.5μm范圍內。因此通過該補償方法能夠消除絕大多數的定位誤差，對于隨機誤差的影響效果也可以控制在理想范圍之內。

6 結論

在目前的研究水平基礎上，本文基于插值法對直線電機定位誤差的補償方法進行研究，提出了采用加權拉格朗日二次插值的方法提高誤差補償的精確度和可靠性，通過實驗驗證，證明了該方法的可行性。在此前提下，從影響直線電機定位精度的主要因素出發進行分析，改進了前饋控制器的控制方式，使控制器輸出的信息能夠有效補償電機因外部環境導致的定位誤差，配合反饋實現更精確的定位。