基于CODHD聚類劃分的多擴展目標跟蹤算法

苗 露，李鴻艷，馮新喜

空軍工程大學 信息與導航學院，西安 710077

1 引言

多目標跟蹤是利用傳感器量測對目標數目和狀態進行估計的過程，主要受到雜波、漏檢和虛警的影響[1]。傳統目標跟蹤所利用的是點目標模型，假設在每一觀測時刻每個目標至多產生一個量測。隨著傳感器分辨率的提高，這種假設不再適用，探測單個目標時會得到多個量測值，即可以得到更多的目標運動和形態信息[2]，這種目標跟蹤稱之為擴展目標跟蹤。

Mahler根據隨機有限集（RFS）理論[3]，推導出概率假設密度（Probability Hypothesis Density，PHD）濾波器的遞推方程，避免了傳統目標跟蹤所利用的復雜數據關聯過程，但存在集值積分無法求解的難題。隨后，Mahler利用RFS的一階統計矩對多目標的后驗概率密度進行近似替代，提出了一階統計矩近似的PHD濾波器，并于2009年將PHD濾波器用于擴展目標跟蹤，即ET-PHD（Extended Target PHD）濾波器。假定目標運動模型滿足線性高斯條件下，文獻[4]給出了高斯混合PHD（Gaussian Mixture PHD，GM-PHD）濾波器的實現，文獻[5]給出了擴展目標高斯混合PHD（ET-GM-PHD）濾波器的實現。文獻[6]利用核密度估計方法對經過剪枝、合并后的PHD密度分布函數進行狀態估計，將峰值點作為狀態估計值，使目標估計結果更加精確。針對目標漏檢時致使有用信息丟失和目標相近造成濾波性能下降，文獻[7]對PHD濾波器的預測、更新方程加以修正，有效改善了目標跟蹤性能。

根據Mahler的推導[8]，無論是ET-PHD濾波器、GMET-PHD濾波器還是GM-ET-CPHD濾波器，提高濾波器性能就需要對量測集進行快速準確的劃分，這在理論上是需要考慮所有可能的劃分。而實際中隨著目標數和雜波量測增多，量測劃分數將急劇增加，將引起計算災難，這對擴展目標跟蹤系統而言，實時性的要求難以滿足[9]。關于量測集劃分問題已經提出了多種解決辦法，Granstrom等[5]提出了距離劃分、距離輔助劃分，Li等[10]提出了K-means聚類劃分，以上方法均是利用距離進行劃分，在量測密度差別較大時效果不佳。Zhang等[11]提出了基于快速模糊自適應共振理論（Adaptive Resonance Theory，ART）的劃分方法，能進行穩定快速的量測集劃分，但在多雜波環境下對多個擴展目標進行跟蹤，算法易出現“飽和”問題而產生額外錯誤劃分。文獻[12]提出CODHD算法，該算法基于凝聚性層次劃分，對簇合并計算過程和聚類有效性指標進行優化，得到最優聚類結果。本文基于該方法進行量測集劃分，先通過自適應橢球門限進行量測預處理使無效雜波有效去除，再利用CODHD得到最優聚類結果，利用FCM運算得到量測劃分子集。

2 ET-GM-PHD濾波器

Mahler在ET-PHD濾波框架下將擴展目標用空間分布模型來描述，假設擴展目標滿足線性高斯運動模型，傳感器觀測滿足線性模型，目標存活概率和檢測概率相互獨立，多擴展目標的預測強度函數就可以通過高斯混合的形式來表示[13]。

假設在k時刻，擴展目標的狀態集表示為Xk=，量測集表示為和分別表示k時刻的第i個擴展目標的狀態和量測，Nx,k和Nz,k分別表示k時刻的擴展目標數和量測數。根據RFS理論，目標的狀態方程為：

其中，i=1,2,…,Nx,k，Fk表示狀態轉移矩陣，表示協方差為的零均值高斯白噪聲。

目標的量測方程為：

其中，Hk表示觀測矩陣，表示協方差為的零均值高斯白噪聲。

在k時刻，預測PHD的GM可表示為：

量測更新PHD強度可通過預測PHD強度和偽似然函數相乘得到，即：

其中，量測偽似然函數為：

式中，λk=βFA,kVs為雜波量測個數的期望，ck(zk)=1/VS為觀測空間中雜波的空間分布，p∠Zk為對Zk的P劃分，W為某一劃分中的各非空集合，ωP和dw分別為P和W的權重。

在每一觀測時刻，每個擴展目標會產生多個量測，而傳感器得到的量測由真實目標量測以及雜波量測構成。假設在k時刻，傳感器獲得量測表示為Zk=則對其進行劃分的所有可能結果為：

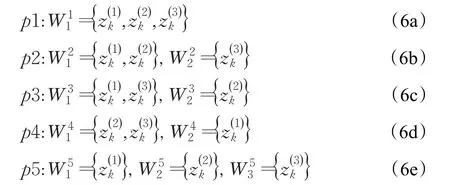
3 量測集劃分

3.1 自適應橢球門限處理

雜波量測離散、均勻分布在觀測空間，若雜波和真實目標量測一同進行劃分，將產生額外錯誤劃分，最終影響濾波效果。在量測集劃分前，可采用橢球門限[14]方法進行量測預處理，在不影響濾波精度的前提下，有效濾除無效雜波來改善跟蹤性能。

假設在k時刻，對預測步進行計算后，第i個觀測和第j個高斯分量的殘差向量表示為：

ε(ji)的協方差矩陣表示為：

通過橢球門限判別對量測進行預處理，滿足：

3.2 基于CODHD算法的量測集劃分

利用聚類實現擴展目標量測集劃分是有效途徑，CODHD算法基于凝聚型層次聚類，在簇合并過程中對生成的不同劃分進行聚類質量評估得到最優聚類結果。該算法對簇合并過程和聚類評估指標加以優化，使計算復雜度降低并提高聚類有效性。

對去除雜波后的量測集劃分過程如下：對量測進行區間掃描生成合理劃分；層次式生成不同量測劃分，計算各劃分中的量測局部密度并將密度最大點作為聚類中心點，得到該中心點和更高密度量測之間的最小距離；將每次得到的聚類質量構造為質量曲線并提取極大值點；通過剪枝[15]原理得到最優聚類結果并進行FCM運算，得到量測劃分子集。

聚類質量評估指標Q定義為：

量測局部密度Ni計算過程如下：

（1）將量測標準差作為鄰域半徑：

（2）在鄰域半徑所構成區域內計算局部密度：

δi表示最小距離，；對于密度最高點有：。Q表示聚類中心量測密度與最小距離乘積之和的均值，若i為聚類中心，則Ni和（或）δi取較大值的可能性就越大，衡量指標Niδi也就有較大值。

凝聚型層次聚類算法在起始階段將每個數據看做單獨子簇，根據簇合并準則將子簇不斷進行合并，最后使所有數據成為一個集合。假設k時刻量測集為Z={z1,z2,…,zn} ∈Rd×n，其中 d 為量測維度，n為量測個數。簇合并過程如下：

（1）初始化 S=S0。

（2）將量測進行屬性值大小排序，生成序列Ai，在有限區間內掃描，尋找量測x的第i維相似量測y。

（3）每過程 S 增大 Δ(Δ={Δ1,Δ2,…,Δd})，并在上一掃描區間基礎上進行擴張，繼續掃描尋找相似量測進行合并：

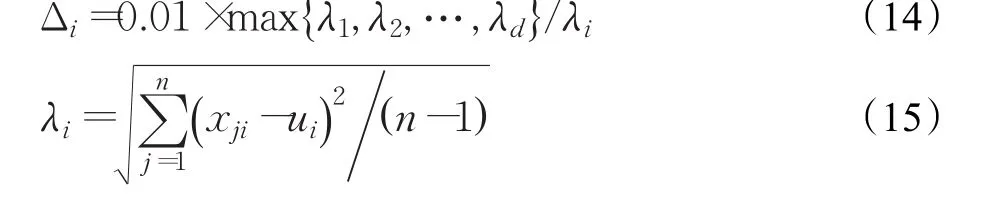
（4）S增大到所有量測劃分到一個集合。

圖1表示在不同劃分數下得到的聚類質量并構造為質量曲線。

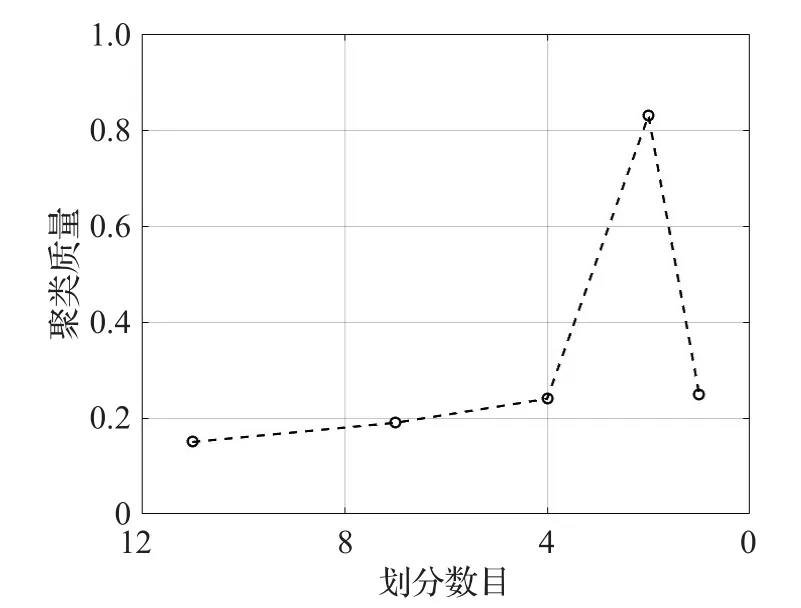
圖1 不同劃分數目下的聚類質量

FCM通過隸屬度決定量測劃分，是傳統硬劃分K-means的改進，對劃分歸屬模糊問題能進行較好處理。將剪枝得到的聚類結果進行FCM操作，可有效改善劃分效果，其實現過程如下：

（1）提取質量曲線極值點，進行剪枝操作得到聚類數l和聚類中心集V0=(v1,v2,…,vl)，進行相關參數設置：權重指數 m(m=2)，終止閾值 ε(ε=0.01)，迭代記步器t=0。

（2）計算、更新劃分矩陣Ut：

（3）更新聚類中心Vt+1：

量測集劃分的典型方法和改進方法有距離閾值法、K-means聚類方法、ART方法等。距離閾值法為保證劃分中能包含正確的劃分子集，需要選取較大的閾值范圍，這造成較多錯誤劃分并使目標狀態估計誤差增大。K-means算法由于K值難以選取且隨機選擇初始聚類中心，致使聚類結果不穩定，在量測密度差異較大時難以進行有效劃分。ART算法對輸入警戒參數β比較敏感，在多擴展目標的多雜波環境下，易造成算法“飽和”問題使權向量無法自適應調整權重以適應訓練模式，產生額外錯誤劃分，使跟蹤效果下降。

基于CODHD聚類劃分算法的量測集劃分在層次簇合并過程中對生成的不同劃分進行聚類評估，得到最優聚類結果后進行FCM運算得到量測劃分子集。由于簇合并過程中簇生成個數只與量測分布結構有關，使其可識別量測密度差異；采用標準差作為鄰域半徑計算量測局部密度，能夠反映量測集的量測真實分布情況[16]；避免對量測數據直接進行反復聚類，自適應生成最佳聚類數和聚類中心后執行FCM運算，有效加快收斂速度。考慮真實擴展目標跟蹤場景，在雜波環境下目標個數未知并隨時間而不斷發生變化，并存在目標緊鄰、分裂、量測生成數未知等情形，這都影響到多目標跟蹤性能。所提方法根據量測分布情況自適應得到最優聚類結果，因此適合于在雜波和目標量測未知情形下進行快速準確地擴展目標量測集劃分，確保目標跟蹤的實時性。

3.3 擴展目標跟蹤算法流程

基于CODHD算法對量測集劃分的擴展目標跟蹤算法流程歸結如下：

（1）已知k-1時刻的目標強度函數Dk-1(x )，預測得到k時刻的目標強度函數

（2）將新生目標和存活目標的高斯分量作為k時刻的狀態預測，進行殘差和橢球門限值的計算，對量測集Zk進行門限處理后只保留門限內的有效量測

（3）參數初始化：k=n,Un={z1,z2,…,zn},S=S0，Qn=Q(Un)，將量測根據第i維屬性排序生成Ai。

（4）從k=n運行至k=1：

②通過簇合并生成新劃分，計算Nx和δx，求得有效性指標Qk；

③生成聚類質量曲線。

（5）提取曲線極值點得到量測劃分，并利用剪枝原理獲得最優聚類數和聚類中心。

（6）進行FCM運算獲得若干量測劃分子集，并將其對目標強度函數進行更新。

4 仿真結果及分析

為證明本文方法的有效性和可行性，假定在二維平面，傳感器對四個擴展目標進行跟蹤，觀測區域為[-500,500]m×[-500,500]m，采樣周期T=1 s，觀測時長為40 s。目標運動和觀測方程均滿足線性高斯模型，各擴展目標的初始狀態以及出生、消失時間見表1。

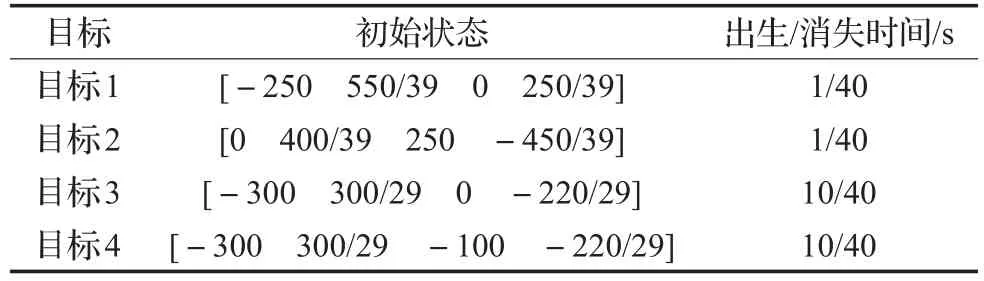
表1 目標初始狀態和運動軌跡

在不考慮目標衍生的條件下，PHD濾波器的新生過程表示為強度是γk的泊松有限集。即：

擴展目標的存活概率Ps,k=0.99，檢測概率PD,k=0.95。每一觀測時刻，擴展目標的量測生成分別服從均值為10、15、20、30的泊松分布，雜波生成量測服從均值為30的泊松分布，并在觀測空間內服從均勻分布。高斯項修剪門限Tp=10-4，最大高斯個數Jmax=200，融合門限U=4，橢球門限參數Pg=0.95。

進行200次蒙特卡洛仿真，將本文方法和距離劃分法、ART劃分法用于ET-GM-PHD濾波器進行比較。采用最優子模式分配（OSPA）距離[17]（參數設置p=2,c=80）對各算法性能做出評估：

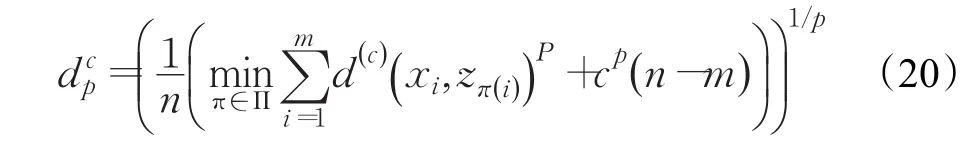
圖2給出了擴展目標在雜波環境下的運動軌跡，圖3和圖4是不同算法得到的目標數估計和OSPA距離對比圖。

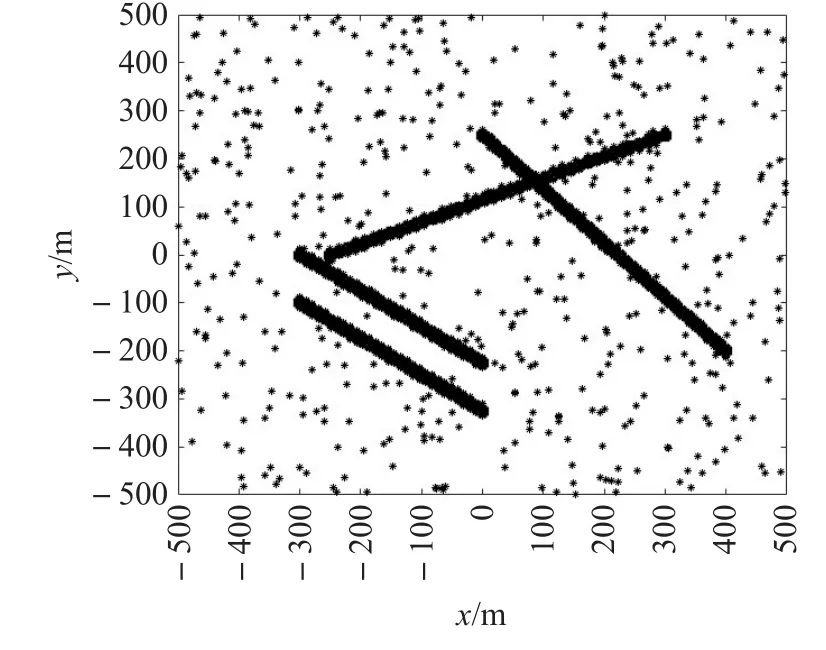
圖2 雜波環境下的目標運動軌跡

由圖3和圖4可知本文方法有更加準確的目標數估計結果以及更小的OSPA距離。這是由于通過橢球門限進行量測預處理使雜波干擾降低，利用量測分布得到最優聚類結果繼續進行FCM運算從而保證聚類劃分準確度，而距離劃分和ART劃分在多雜波環境下進行多擴展目標跟蹤均產生了較多錯誤劃分，致使跟蹤效果下降。

圖3 目標數目估計比較

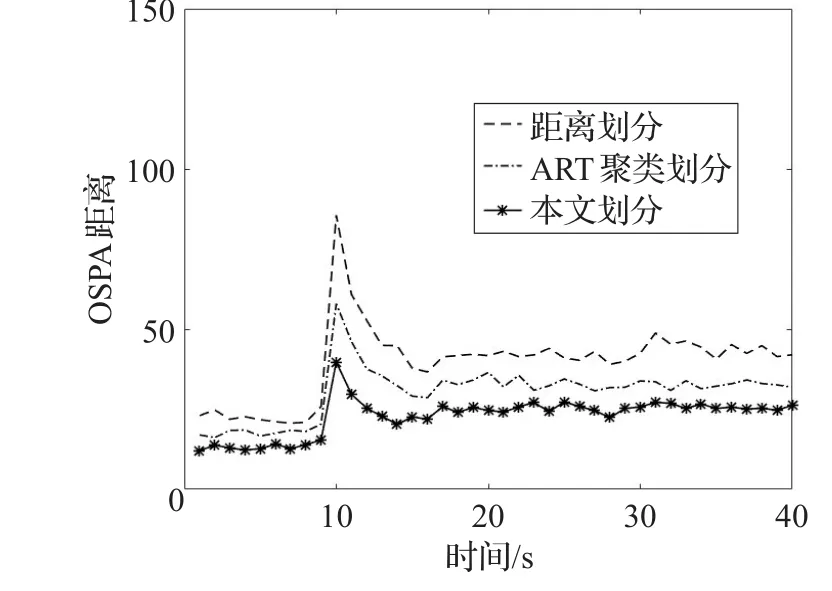
圖4 OSPA距離比較

由圖5可知，本文劃分方法具有較高的運行效率，這是因為在預處理階段將雜波進行了有效濾除使后續劃分算法的計算復雜度降低，利用CODHD輸出最優聚類結果避免了對量測數據直接進行反復聚類并使FCM收斂速度加快。

圖5 劃分時間比較

5 結束語

針對雜波環境下，概率假設密度濾波器對擴展目標跟蹤存在量測集劃分難且效率低的問題，提出基于CODHD聚類算法進行劃分的方法。先利用橢球門限將量測集中的無效雜波量測進行去除，再通過CODHD聚類劃分得到最優聚類結果，進行FCM運算得到量測劃分子集。結果表明所提方法可以對量測集進行快速準確的劃分，保證在雜波環境下對多擴展目標的實時跟蹤。