五種類型不定積分問題的求解

唐夢鑫，朱 華

（攀枝花學院，四川 攀枝花 617000）

1 引言

微積分學的創立極大地推動了數學的發展.過去很多用初等數學無法解決的問題,運用微積分,問題往往迎刃而解,顯示出微積分學的非凡威力.不定積分在微積分中占有至關重要的地位,而不定積分的計算對于大多數初學者來說是一個難點,筆者結合自身所學和實際所遇到的問題,將不定積分求解問題歸為五種類型,并舉例加以說明.

2 基本定義及性質

2.1 若在某個區間I上,函數F（X）和f(x)滿足以下關系

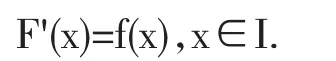
則稱F(x)是f(x)在這個區間I上的一個原函數.

2.2 函數f(x)的原函數全體稱為這個函數的不定積分,記作

3 五種類型的不定積分

3.1 簡單函數不定積分

直接用積分公式或者運算性質求解不定積分,或者將被積函數經過恒等變形 (三角變形,代數變形),代換(三角代換,整體代換,倒代換)后再利用積分公式或者運算性質求解.

例1計算

解

3.2 有理函數不定積分

由代數學基本定理可知:每個次數≥1的有理系數多項式都能唯一的分解成不可約的有理系數多項式的乘積.在求復雜的有理函數不定積分時,可將復雜的不定積分分解成簡單的不定積分后再求解.

例2計算

解根據代數基本定理可將x2+3x-10分解成(x-2)(x+5)的形式.

解得:A=B=1.

3.3 無理函數不定積分

例3計算

解令,則有

由于

因此上述無理根式的不定積分也就轉化為以下三種類型之一:

當分別令 u=ktant，u=ksect，u=ksint后, 它們都轉化為三角有理式的不定積分.

例4

解被積函數的存在域為-∞＜x＜+∞,因此,令x=atant,并限制.從而

代入得

3.4 三角函數不定積分

對于三角函數不定積分的求解,最通用的方法就是萬能公式法,但由于萬能公式過于復雜,所以除非萬不得已一般不采用萬能公式.最常用的方法就是將其通過誘導公式恒等變形,再利用換元法,積分法進行求解.

例5計算

解

3.5 超越函數的不定積分

所謂的超越函數就是指:將三角函數,反三角函數,對數函數,指數函數等初等函數中的一個或多個函數混合成一個函數.在解超越函數不定積分時最基本的方法就是分部積分法,將一個超越函數不定積分分解成多個不定積分分別求解,再利用不定積分的線性性質求和.

例6計算

解

4 總結

觀察對比以上五種類型的不定積分,我們可以發現它們都有共同點:無論是何種類型的不定積分,做何種變換,其目的都是將繁瑣的不定積分等價轉化成最簡單的不定積分,再套用公式求解.