線切割平面線圈Halbach永磁直線電動機電磁分析

張宗慶，馬樹元，宋寧冉

(北京理工大學，北京 100081)

0 引 言

大行程、高精度是定位平臺追求的目標,而磁懸浮直線電動機是滿足這一要求的途徑之一。直線電動機磁懸浮力與水平推力由氣隙磁場決定，而定子線圈平面精度直接影響氣隙磁場形態與大小。因此，定子線圈平面精度是影響直線電動機驅動穩定性的重要因素之一[1]。

直線電動機是磁懸浮運動平臺直線運動的電磁驅動裝置，永磁同步直線電動機可以看作是永磁同步旋轉電機沿徑向剖開，直線電動機的縱向、法向和橫向與旋轉電動機周向、徑向和軸向一一對應。基于David L.Trumper對永磁直線電動機框架結構和原理的分析[2]，Won-Jong Kim建立的基于Halbach永磁陣列的直線電動機數學解析模型成為許多學者進行直線電動機電磁分析的理論基礎[3]。周贛等在對Halbach陣列磁場解析計算和諧波分析的基礎上[4]，對Halbach型直線電動機執行器的特點進行分析，并提出其電磁力方程[5]。宋玉晶則在考慮端部效應的基礎上建立無鐵心式永磁同步直線電動機推力模型[6]。支凡等通過建立永磁直線電動機推力諧波解析模型，并將低推力波直線電動機設計準則應用于直線電動機優化設計中，降了低推力波動[7]，王斐然等則提出最優初級長度從而抑制了永磁直線電動機的推力波動[8]。潘開林等分析了永磁直線電動機磁阻力產生的原因，并提出相應的抑制永磁直線電動機磁阻力削弱的措施[9-10]。

對于直線電動機，目前學者研究側重點在于Halbach 磁體結構，對線圈研究較少，文獻[2-11]中很多定子繞組均采用環型線圈表面纏繞結構。Han-Sam Cho根據線圈陣列與永磁陣列相互作用的平面驅動原理，提出了一種多組一維線圈陣列和一個二維永磁陣列所組成的動線圈式平面電機[11]。此后，不少學者對平面電機有了較為深入的研究，諸如文獻[13-15]。平面電機所用線圈類型有圓形線圈、同心環形線圈、魚骨形線圈等，定子有帶鐵心和無鐵心之分。

謝虎等采用漆包線粘接成平面線圈并進行了電磁分析[15]，徐偉等對凸型Halbach陣列的永磁直線電動機磁場進行分析[16]。在此工作的基礎上，本文對線切割平面線圈Halbach永磁直線電動機進行電磁分析，并進一步驗證其優良性。

1 磁懸浮直線電動機結構

在磁懸浮系統中，直線電動機一般由固定的平面線圈作為定子，浮動的凸型Halbach永磁陣列(固定于工作平臺上)為動子。直線電動機依靠Halbach永磁陣列的磁場與通電平面線圈產生的勵磁磁場相互作用產生的電磁力進行驅動[15]。

磁懸浮Halbach永磁直線電動機模型如圖1所示，IA,IB′,IC,IA′,IB,IC′為三相對稱正弦電流，磁塊上所標箭頭表示磁塊充磁方向，4個方向為一周期。分段的凸型永磁體來構成Halbach 永磁陣列，形成較理想化的空間正弦分布磁場。永磁陣列的磁場與通電平面線圈產生的氣隙磁場相互作用產生電磁浮力[16]，將永磁陣列懸浮至控制高度0.5 mm；同時產生電磁推力，在線圈固定的情況下，工作平臺將沿著行波磁場運動的方向作直線運動。當永磁直線電動機的線圈平面精度達不到設計精度時，將會直接影響磁懸浮定位平臺的精度及運動穩定性。

圖1磁懸浮Halbach永磁直線電動機模型

對交流線圈繞組，一般要求三相繞組對稱，電動勢和磁動勢的波形接近正弦波，機械強度高，散熱好，絕緣性能可靠，制造工藝簡單。傳統環形線圈在加工制造過程中的不對稱，會導致各相線圈的互感不相等，引起端部效應；制造過程中不易保證線圈平面的平面度，影響電機的平穩工作，無法滿足高精度的需求。特別是對于磁懸浮直線電動機，由于沒有懸浮方向的約束，線圈平面在懸浮方向的精度直接影響電機在懸浮方向上的平穩性。

本文設計了平面線圈結構，由線切割加工而成，通過加工精度的控制保證三相繞組的對稱性，最大限度地克服端部效應的影響，并保證線圈平面優良的平面度。在裝配時采取彎折措施，利于配線組裝。為使線圈平面獲得更高的平面度，還可在組裝后做磨削加工，然后對表面進行絕緣處理。

2 平面線圈電磁分析

2.1 平面線圈邊界磁矢勢分析

永磁直線電動機電磁分析模型如圖2所示。其中fx為水平X方向電磁推力，用于在X方向平臺實現指定位移；x0為永磁體相對于定子的水平位移；fz為懸浮Z方向磁懸浮力,用于將工作平臺懸浮至指定高度并保持；z0為空氣間隙厚度；Δ為永磁體的厚度；Γ1為平面線圈厚度;l為永磁陣列周期長度；字母a～h表示物體的邊界；IA,IB′,IC,IA′,IB,IC′為三相對稱正弦電流；J為電流密度；磁塊上所標箭頭表示磁塊充磁方向，4個方向為一周期。

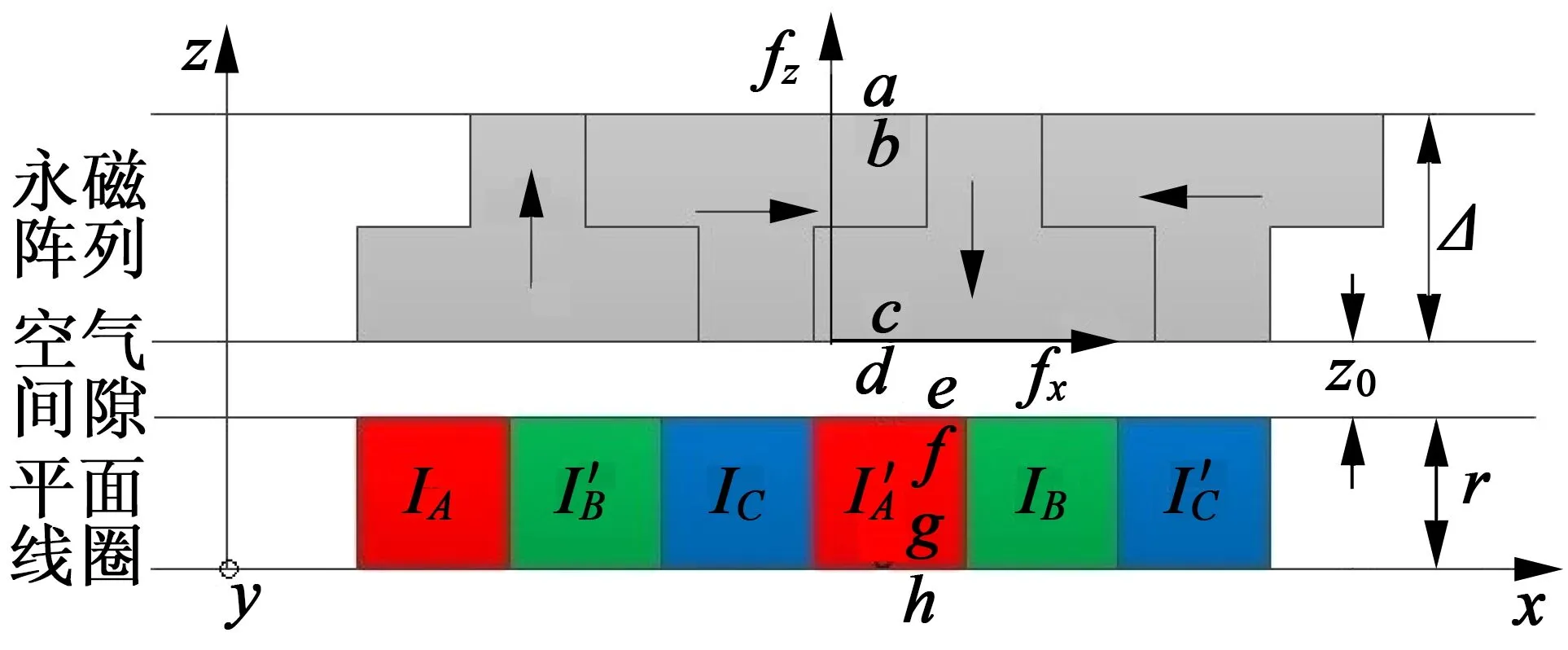
圖2 永磁直線電動機模型圖

在平面線圈電流IA,IB′,IC,IA′,IB,IC′區域內，磁矢勢方程：

(1)

在平面線圈內泊松方程的特解：

(2)

式中：kn為表面電流線密度；μ0為真空磁導率。

平面線圈邊界f和g的磁場：

(3)

在平面線圈區域內的磁感應強度與磁矢勢關系：

(4)

(5)

邊界h和g磁矢勢關系：

(6)

(7)

求解式(1)～式(7)，可得：

(8)

(9)

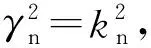
(10)

(11)

可得空氣間隙上表面d的磁感應強度：

(12)

可得平面線圈邊界e的磁矢勢：

(13)

2.2 平面線圈電磁力分析

平面線圈中的磁通量確定以后才能得到其感應電動勢，根據斯托克司定理可知，平面線圈磁通量可用磁矢勢表示：

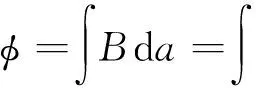
(14)

平面線圈的磁場周期為L，相數為φ1,ω為線圈長度，平面線圈磁通量φ：

(15)

(16)

式中：η0為線圈電流密度。

電流密度J的Fourier可表示：

(17)

磁矢勢：

(18)

則平面線圈磁通表達式：

(19)

從式(19)可得，平面線圈磁通量φ與線圈厚度Γ和磁場周期L有關。

在直線電動機電磁功率確定之后，才能確定直線電動機的水平驅動力fx和懸浮力fz與平面線圈結構的關系。

直線電動機機械功率PM：

PM=vxfx+vzfz

(20)

在工作時，直線電動機電磁功率PE轉化為機械功率PM，采用平面線圈的直線電動機，電磁功率PE：

(21)

做以下假設： 平面線圈電流密度Jz在z方向正弦分布；對電磁功率影響較小的高次諧波忽略不計；只考慮對電磁功率影響較大的基波。得Jz表達式：

Jz=(Ja+jJb)e-jk1z+(Ja-jJb)e-jk-1z

(22)

將式(22)代入式(21)并根據關系式(23)：

γ-1=γ1=k-1=k1

(23)

可得電磁功率PE：

PE=μ0M0Ge-γ1x0{vx[Jasin(γ1z0)-Jbcos(γ1z0)]-

vz[Jacos(γ1z0)+Jbsin(γ1z0)]}

(24)

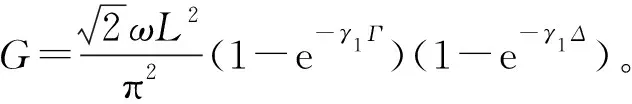
直線電動機輸入電磁功率PE和輸出機械功率PM相等(能量守恒定律)，綜合以上各式可得：

(25)

式中：μ0M0及γ1均為永磁體物理常量；線圈厚度Γ和電流密度J的關系：

(26)

由式(25)和式(26)可得:

(27)

由式(27)可知，當永磁陣列參數確定后，平面線圈輸入電流I，厚度Γ和線圈磁場周期L共同決定了直線電動機的磁懸浮力fz與水平推力fx，在線圈磁場周期L和厚度Γ確定的情況下，磁懸浮力fz與水平推力fx只由電流I決定。

3 線圈的設計和制作

線圈組裝后如圖3所示。直線電動機在定子和動子的磁場周期相等時才能正常工作，由凸形[1]Halbach永磁陣列周期長度為24 mm，可得平面線圈每一相的寬度應該為24 mm/6=4 mm。根據前面分析及直線電動機驅動力要求，結合磁懸浮系統工作平臺運動需求，線圈厚度設為1 mm，采用雙層結構，上下兩層串聯，三相繞組Y型連接。兩端孔是為方便連線。考慮到導電性以及成本因素，材料選擇紫銅。考慮到實際永磁陣列的制造、安裝等誤差，以及線圈的制造、安裝絕緣處理等誤差，留有間隙，以抵消實際誤差，達到永磁陣列的周期與線圈周期相匹配。利用三坐標測量機測量本文線圈的平面度為0.084 7 mm，較之前所用線圈的平面度有較大改善[15]。

圖3 線圈組裝圖

4 平面線圈有限元仿真分析

為了對設計的直線電動機的電磁特性進行進一步分析，采用COMSOL軟件建立了線圈的2D有限元模型，并設定如表1所示的相關參數，分析得到的線圈產生的磁場分布如圖4所示。根據磁懸浮平臺的設計懸浮高度，在0.5 mm處產生的行波磁場如圖5所示。可以看出，本文研究的平面線圈繞組磁場，特別是接近中間工作區域，正弦性接近理想形態，加之較高的平面精度，適合作為系統Halbach永磁直線電動機的定子繞組使用。

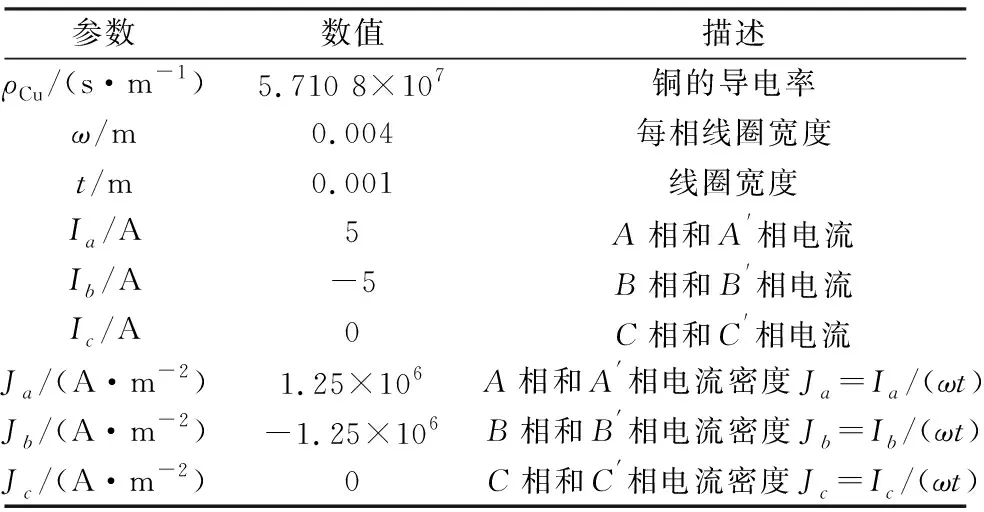
表1 平面線圈有限元仿真參數

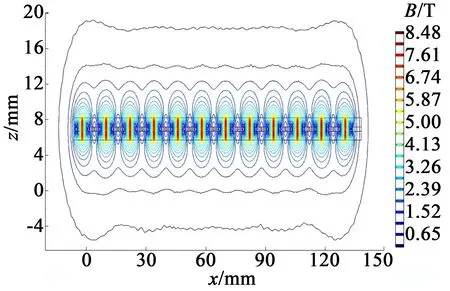
圖4 線圈的2D有限元模型磁場強度分布圖

圖5 0.5 mm處產生的行波磁場

5 直線電動機有限元分析仿真

為求得直線電動機電磁密度進而得到系統的電磁力，需要對直線電動機進行電磁分析。COMSOL基于洛倫茲力法求解電磁力，即把通電平面線圈當作載流設備，可得通電平面線圈在水平X方向和懸浮Z方向所受的洛倫茲度密度，基于洛倫茲力密度公式F=J×B，即可得平面線圈所受的磁懸浮力和水平推力，即為磁懸浮系統的磁懸浮力fz與水平推力fx。

建立平面線圈凸形Halbach永磁直線電動機的模型并導入COMSOL，如圖6所示。

圖6平面線圈直線電動機有限元仿真模型

COMSOL分析過程中，相關常數及參數如表2所示。

表2 直線電動機COMSOL仿真參數

建立好直線電動機的仿真模型, 定義有限元網格、 選擇求解器和可視化結果之后，得到如圖7所示結果。

圖7 直線電動機有限元仿真磁場強度分布圖

在COMSOL后處理中，選擇所有的線圈進行求解域積分，得到通電線圈的在Z方向和X方向洛倫茲力密度系數分別為59.745 N/m和33.028 N/m，乘以平面線圈與永磁陣列作用的有效長度0.04 m，可得線圈所受到的洛倫茲力：懸浮Z方向2.389 8 N，水平X方向1.321 N，根據作用力與反作用力原理，直線電動機永磁陣列受到的懸浮力fz為2.389 8 N,水平推力fx為1.321 N。

在對直線電動機進行系統仿真時，為簡化仿真模型，并沒有考慮運動平臺和永磁阻尼器的重量與影響，此時運動部件的重量為0.21 kg，即所受的重力：

G=mg=2.058 N

(28)

由仿真結果及式(28)可知，當平面線圈厚度為1 mm時，磁懸浮力fz=2.389 8 N>G,能夠滿足磁懸浮系統驅動要求，此時fx=1.321 N，能夠滿足磁懸浮系統加速度要求。同時仿真結果進一步驗證了采用平面線圈的凸形Halbach永磁直線電動機設計的正確性。

6 結 語

本文研究了用以改進磁懸浮平臺Halbach永磁直線電動機定子平面精度的線切割平面線圈，在制作工藝和線圈平面的平面度方面有較大提升，而且易于裝配。針對所設計的線圈，利用有限元方法分析了電磁特性分析。結果表明平面線圈繞組磁場正線性接近理想形態，適合作為系統Halbach永磁直線電動機的定子繞組使用。因此，Halbach永磁直線電動機中，使用本文設計的線切割平面線圈，能夠使電機運行更平穩，改善磁懸浮平臺的精度及運動穩定性。