基于ANSYS Workbench的汽車盤式制動器性能分析
桑振竹,丁振森,楊行,李浩燃,許豪
(長安大學汽車學院,陜西 西安 710064)
引言
本文以盤式制動器為研究對象,在CATIA中建立三維模型并導入ANSYS Workbench中,對其零部件進行了強度及模態分析,得出了零部件所受的最大應力、固有頻率及振型[1]。并在此基礎上分析了制動盤尖叫產生的原因。
1 有限元模型的建立
1.1 幾何模型
本文以某小轎車前制動盤作為研究對象,所采用的制動盤在盤面上本來有許多為散熱而設計的小孔,經過測量半徑不足5mm,對最終的仿真結果影響不大,因此本文在建模過程中忽略這些小孔。本文采用圓形板件,材料采用結構鋼,屈服強度為345Mpa。如圖1所示為該制動盤的CATIA結構圖。
1.2 網格劃分
1)模型簡化
首先為減少計算的工作量,同時還要保證單元的質量。因此在劃分網格之前要對模型進行適當簡化。
2)單元理論
本模型采用ANSYS Workbench軟件中提供的實體單元(Solid187單元)進行網格劃分。

圖1 制動盤的CATIA結構圖
3)網格劃分生成有限元模型
(1)在ANSYS Workbench軟件平臺建立靜力學分析模塊,項目中導入制動盤的有限元模型,進行自由網格劃分,單位選擇為(mm, t, N, s, mv, mA)。
(2)在把模型導入到ANSYS Workbench軟件的靜力學分析模塊之后,需要給所導入的模型添加定義材料屬性,整個制動盤的材料為一種,即結構鋼。該材料的物理屬性見表1。

表1 結構鋼材料特性
具體操作步驟如下:此步驟在靜力學分析模塊中的Engineering Data里面完成,在工程數據里材料屬性設置為結構鋼,彈性模量為 1.75E11pa,泊松比為 0.3,密度為 7800 kg/m3。
本論文采用Tetrahedrons 中的Patch Conforming 法,它是可以快速地、自動地生成網格,并適合于復雜幾何體。網格劃分完成后的制動盤有限元模型如圖2所示。

圖2 制動盤有限元模型
1.3 單元及節點信息
本文對研究的制動盤進行網格劃分時,綜合制動盤的結構、精度要求及計算時間考慮,選擇單元尺寸長度為0.005m進行整體劃分,該制動盤共包括34489個節點,共有17899個單元。
2 制動盤強度分析
2.1 約束和載荷確定
(1)定義約束,對制動盤中心孔面施加全約束,對盤體內外端面施加X向約束,對制動盤與摩擦片接觸的摩擦面施加Y向和Z向約束。
(2)施加載荷,對摩擦片接觸的兩側摩擦面均施加的25MP的載荷。
2.2 制動盤結構靜力分析
對制動盤結構的強度進行計算和分析,在導航項中添加求解結果顯項變形和應力,然后求解。應力的求解結果云圖如圖3所示。
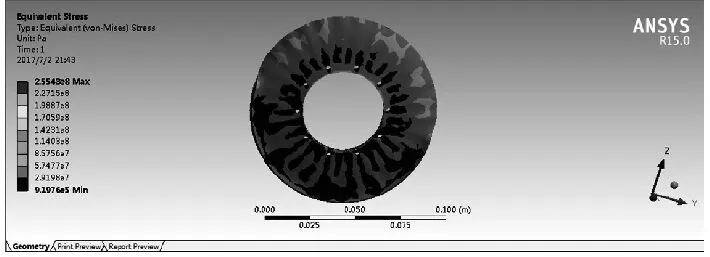
圖3 制動盤等效應力云圖
通過制動盤的應力云圖可知,該制動盤在制動過程中所承受的最大應力值為 255.43MP,而該制動盤的屈服強度為345MP,因此該制動盤完全滿足強度要求。
變形云圖如圖4所示。
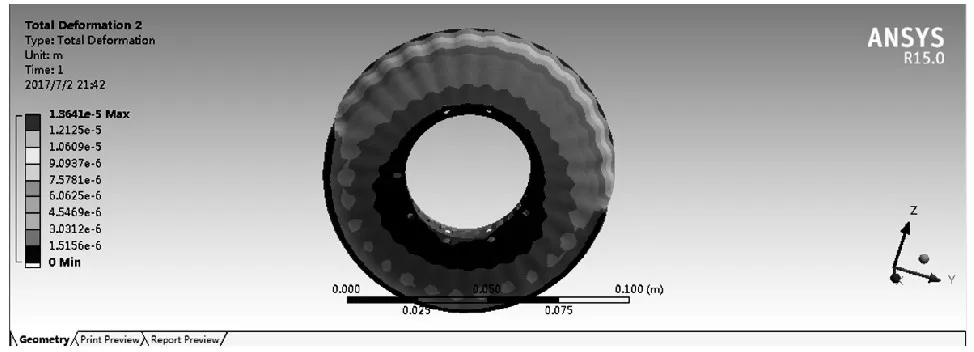
圖4 制動盤的變形云圖
由變形云圖可知,該制動盤在制動過程中的最大變形為0.0136mm,并且越靠近中心位置變形越小。
3 制動盤的模態分析
制動盤是一個在外界的時變激勵作用下將產生振動的彈性系統。共振與系統的固有頻率有關。當外界激振頻率接近于固有頻率時(即共振)不僅不利于制動安全性,而且還會加速部件疲勞,產生噪聲,使制動盤的壽命和使用性能受到嚴重影響。系統的固有頻率可通過模態分析求得并且還能得到其它振型[2]。因此,對車架現有結構進行模態分析是確定結構是否產生共振現象的良好方法。
3.1 模態分析的過程與結果
模態分析需要在ANSYS Workbench軟件的模態分析模塊進行,然后再導入制動盤的幾何模型,設置材料屬性,對制動盤劃分網格,最后求解得到制動盤的模態分析結果,由于本文所研究的制動盤與之前作靜力分析的制動盤是一個制動盤,因此,直接用靜力分析模塊的參數即可。
提取制動盤的前十階模態頻率值及振型描述如表2。
由以上的前十階頻率分布表可知,該制動盤的最低階頻率及一階頻率為4072.1HZ,而通過查閱資料可知,盤式制動器的尖叫頻率約在 2100Hz左右,因此該制動器的設計可以避開尖叫頻率,不會引起尖叫。

表2 制動盤的頻率描述
從該車制動盤的前十階自由模態可以發現,其固有頻率絕大部分是在的圓頻率范圍內,按圓頻率ω與頻率f之間的對應公式:
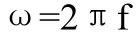
可知,制動盤前十階模態固有頻率大多在10000以內,車輛行駛運轉的過程中出現這樣的頻率的可能性比較小[3]。因此,該制動盤通過模態分析可以發現,其固有頻率基本上避開了尖叫頻率以及路面上行駛可能出現的頻率,出現共振的可能性比較小,因此,該制動盤的設計基本滿足要求。
4 結論
本文運用有限元法對某小轎車的前制動盤進行了靜力學分析、模態分析,并對結果進行了分析比較,對制動盤特性作出了評價。對制動盤的結構簡化、降低成本具有重要的指導意義。

