Pm和Pn的強直積的強邊染色

譚亞茹，馬登舉

（南通大學理學院，江蘇 南通 226019）

設V（G）、E（G）分別表示圖G的頂點集和邊集.圖 G 的 k-邊正常染色是指映射 f：E（G）→{1，2，…，k}，使得對圖G中任意相鄰的邊e1、e2，均有.設e1、e2是圖G的2條不相鄰的邊，e1的一個端點到e2的一個端點且不經過e1和e2的路稱為e1到e2的一條路，其中最短的一條路所含的邊數稱為e1到e2的距離.圖G的強邊染色是圖G的一個正常邊染色，滿足任意2條距離小于或等于1的邊染色不相同.在圖G的所有強邊染色中，使用顏色最少的強邊染色所含顏色的數目稱為G的強邊色數，記為χS′（G）.1985年，Erdos和Nestil提出猜想[1]：當一個圖的最大度Δ分別為偶數和奇數時，其強邊色數分別不超過5Δ2/4和（5Δ2-2Δ+1）/4.之后相關學者對強邊染色進行了研究.文獻[2-3]研究了圍長不小于6的平面圖的強邊染色，得到這類圖強邊色數的上界；文獻[4]給出了2個圖笛卡爾積和強積的強邊色數的上界或下界；還有一些文獻[5-7]對一些特殊圖給出了其強邊色數的確切值.

令G1、G2是階至少為2的簡單圖.圖G1與G2的強直積G1G2是這樣的一個圖，其頂點集合為V（G1G2）=V（G1）× V（G2），邊集合為

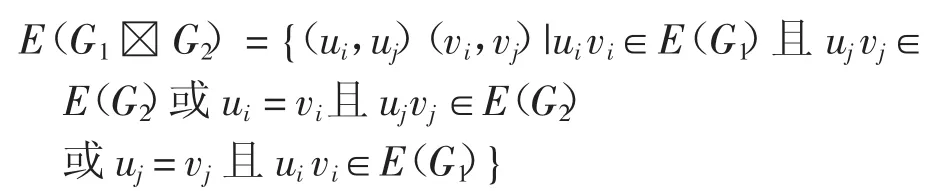
文獻[4]證明了對于簡單圖G1和G2的強直積G1G2，有

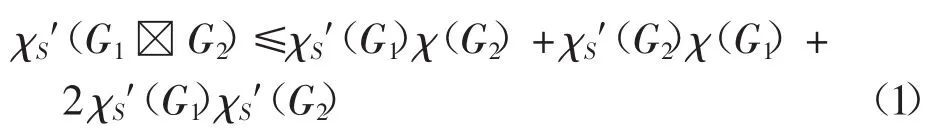
這里χ（H）表示H的色數.

設F是一個至少有2個頂點的路.因F是一個二部圖，故F的色數為2.不難發現F的強邊色數至多為3.設Pl表示有l個頂點的路.當m≥2，n≥2時，由式（1）有χS′（PmPn）≤30.本文得到如下結果：當m=2，n≥3時，χS′（PmPn）=14；當m=3，n≥3時，χS′（PmPn）=20；當m≥4，n≥4時，χS′（PmPn）=26.

定理1當n≥3時，χS′（P2Pn）=14.

證明先證明 χS′（P2Pn）≥14.設 H1是一個有8個頂點的圖，如圖1所示.顯然H1中任意2條邊之間的距離都不大于1.而圖H1含有14條邊，所以χS′（H1）≥14.因為圖P2Pn有一個子圖同構于圖H1，所以χS′（P2Pn）≥χS′（H1）≥14.

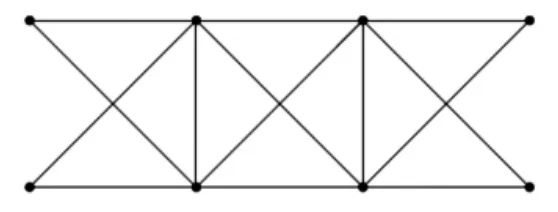
圖1 與P2Pn的子圖同構的H1Fig.1 H1that is isomorphic with a subgraph of P2Pn

再證明 χS′（P2Pn）≤14.只需給出 P2Pn的一種使用14種顏色的強邊染色即可.設P2Pn的頂點集為 V={vi，j|i=1、2；j=1，2，3，…，n}，將 P2Pn的邊分為 4 個子集合 E1、E2、E3、E4，其中：

定義P2Pn的一個邊染色f.

（1）在E1上：若j≡1（mod3），則f（v1，jv1，j+1）=7；若j≡2（mod3），則f（v1，jv1，j+1）=8；若j≡0（mod3），則f（v1，jv1，j+1）=9；若j≡1（mod3），則f（v2，jv2，j+1）=10；若j≡2（mod3），則f（v2，jv2，j+1）=11；若j≡0（mod3），則f（v2，jv2，j+1）=12.

（2）在E2上：若j≡1（mod2），則f（v1，jv2，j）=13；若j≡0（mod2），則f（v1，jv2，j）=14.

（3）在E3上：若j≡1（mod3），則f（v1，jv2，j+1）=1；若j≡2（mod3），則f（v1，jv2，j+1）=3；若j≡0（mod3），則f（v1，jv2，j+1）=5.

（4）在E4上：若j≡1（mod3），則f（v2，jv1，j+1）=2；若j≡2（mod3），則f（v2，jv1，j+1）=4；若j≡0（mod3），則f（v2，jv1，j+1）=6.

圖P2P6在f之下的邊染色如圖2所示，不難驗證 f是一個強邊染色.綜上有 χS′（P2Pn）≤14.故χS′（P2Pn）=14.

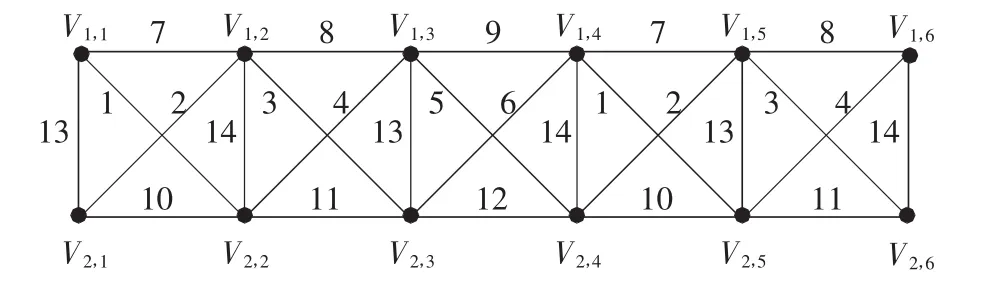
圖2 圖P2P6的強邊染色Fig.2 Strong edge-coloring of P2P6

定理2當n≥3時，χS′（P3Pn）=20.

證明先證明 χS′（P3Pn）≥20.設 H2是一個有12個頂點的圖，如圖3所示.顯然H2中任意2條邊之間的距離都不大于1，而圖H2含有20條邊，所以χS′（H2）≥20.因為 P3Pn有一個子圖同構于圖 H2，所以χS′（P3Pn）≥χS′（H2）≥20.

圖3 與P3Pn的子圖同構的H2Fig.3 H2that is isomorphic with a subgraph of P3Pn

再證明 χS′（P3Pn）≤20.只需給出 P3Pn的一種使用20種顏色的強邊染色即可.設P3Pn的頂點集為 V={vi，j|i=1、2、3；j=1，2，3，…，n}，將 P3Pn的邊分為 4 個子集合 E1、E2、E3、E4，其中：

定義P3Pn的一個邊染色f.

（1）在 E1上：當 i≡1（mod2）時，若j≡1（mod3），則f（vi，jvi，j+1）=11，若j≡2（mod3），則f（vi，jvi，j+1）=12，若j≡0（mod3），則f（vi，jvi，j+1）=13；當i=2時，若j≡1（mod3），則f（v2，jv2，j+1）=14，若j≡2（mod3），則f（v2，jv2，j+1）=15，若j≡0（mod3），則f（v2，jv2，j+1）=16.

（2）在E2上：若j≡1（mod2），則f（v1，jv2，j）=17，f（v2，jv3，j）=19；若j≡0（mod2），則f（v1，jv2，j）=18，f（v2，jv3，j）=20.

（3）在 E3上：設 j≡k（mod5）.若k=1、2、3、4，則f（v1，jv2，j+1）=2k-1，若k=0，則f（v1，jv2，j+1）=9；若k=1、2、3，則f（v2，jv3，j+1）=2k+3，若k=4，則f（v2，jv3，j+1）=1，若k=0，則f（v2，jv3，j+1）=3.

（4）在 E4上：設 j≡k（mod5）.若k=1、2、3、4，則f（v2，jv1，j+1）=2k，若k=0，則f（v2，jv1，j+1）=10；若k=1、2，則 f（v3，jv2，j+1）=2k+6，若k=3、4，則 f（v3，jv2，j+1）=2k-4，若k=0，則f（v3，jv2，j+1）=6.

圖P3P8在f之下的邊染色如圖4所示，不難驗證 f是一個強邊染色.綜上有 χS′（P3Pn）≤20.故χS′（P3Pn）=20.

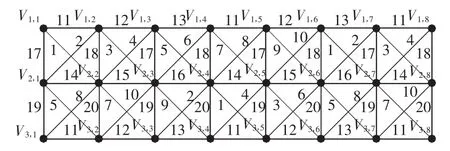
圖4 圖P3P8的強邊染色Fig.4 Strong edge-coloring of P3P8

定理3當n≥4時，χS′（P4Pn）=26.

證明先證明 χS′（P4Pn）≥26.設 H3是一個有16個頂點的圖，如圖5所示，圖H3含有26條邊，類似定理2可得χS′（P4Pn）≥χS′（H3）≥26.

圖5 與P4Pn的子圖同構的H3Fig.5 H3that is isomorphic with a subgraph of P4Pn

再證明 χS′（P4Pn）≤26.只需給出 P4Pn的一種使用26種顏色的強邊染色即可.設圖P4Pn的頂點集為 V={vi，j|i=1、2、3、4；j=1，2，3，…，n}，將圖P4Pn的邊分為 4 個子集合 E1、E2、E3、E4，其中：

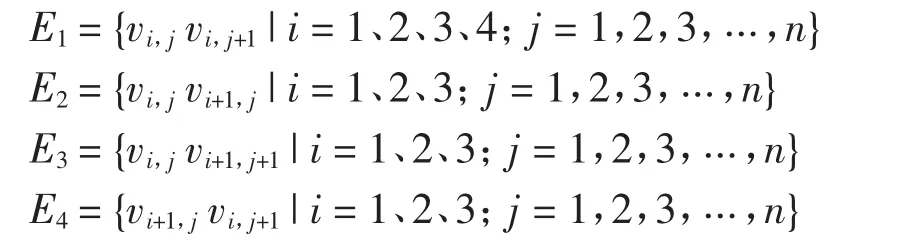
定義P4Pn的一個邊染色f.

（1）在 E1上：當 i≡1（mod2）時，若j≡1（mod3），則f（vi，jvi，j+1）=21，若j≡2（mod3），則f（vi，jvi，j+1）=22，若j≡0（mod3），則 f（vi，jvi，j+1）=23；當 i≡0（mod2）時，若j≡1（mod3），則f（vi，jvi，j+1）=24，若j≡2（mod3），則f（vi，jvi，j+1）=25，若j≡0（mod3），則f（vi，jvi，j+1）=26.

（2）在E2上：若j≡1（mod2），則f（v1，jv2，j）=15，f（v2，jv3，j）=17，f（v3，jv4，j）=19；若j≡0（mod2），則f（v1，jv2，j）=16，f（v2，jv3，j）=18，f（v3，jv4，j）=20.

（3）在 E3上：設 j≡k（mod7）.若k=1、2、3、4、5、6，則f（v1，jv2，j+1）=2k-1，f（v3，jv4，j+1）=2k+1，若k=0，則f（v1，jv2，j+1）=13，f（v3，jv4，j+1）=1；若k=1、2、3，則f（v2，jv3，j+1）=2k+7，若k=4、5、6，則f（v2，jv3，j+1）=2k-7，若k=0，則f（v2，jv3，j+1）=7.

（4）在 E4上：設 j≡k（mod7）.若k=1、2、3、4、5、6，則f（v2，jv1，j+1）=2k，若k=0，則f（v2，jv1，j+1）=14；若k=1、2、3、4，則f（v3，jv2，j+1）=2k+6，若k=5、6，則f（v3，jv2，j+1）=2k-8，若k=0，則f（v3，jv2，j+1）=6；若k=1，則f（v4，jv3，j+1）=14，若k=2、3、4、5、6，則f（v4，jv3，j+1）=2k-2，若k=0，則f（v4，jv3，j+1）=12.

圖P4P10在f之下的邊染色如圖6所示，不難驗證 f是一個強邊染色.綜上有 χS′（P4Pn）≤26.故χS′（P4Pn）=26.

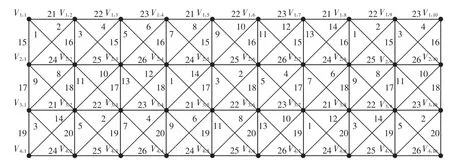
圖6 圖P4P10的強邊染色Fig.6 Strong edge-coloring of P4P10

定理4當m>4，n≥4時，χS′（PmPn）=26.

證明由定理3可知χS′（PmPn）≥26.下面證明χS′（PmPn）≤26.只需給出PmPn的一種使用26種顏色的強邊染色即可.設圖PmPn的頂點集為V={vi，j|i=1，2，…，m；j=1，2，…，n}，將圖 PmPn的邊分為 4 個子集合 E1、E2、E3、E4，其中：

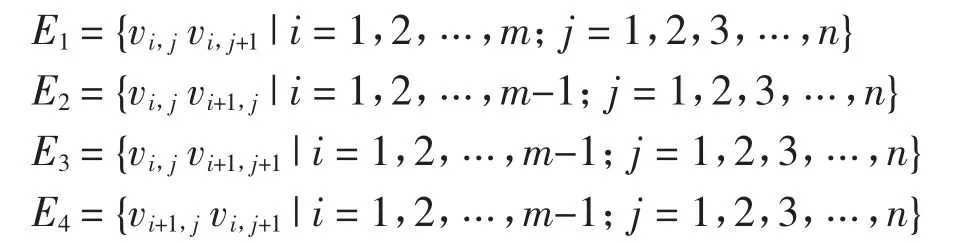
定義PmPn的一個邊染色f.

（1）在 E1上：當 i≡1（mod2）時，若j≡1（mod3），則f（vi，jvi，j+1）=21，若j≡2（mod3），則f（vi，jvi，j+1）=22，若j≡0（mod3），則 f（vi，jvi，j+1）=23；當 i≡0（mod2）時，若j≡1（mod3），則 f（vi，jvi，j+1）=24，若j≡2（mod3），則f（vi，jvi，j+1）=25，若j≡0（mod3），則f（vi，jvi，j+1）=26.

（2）在 E2上：當 i≡1（mod3）時，若j≡1（mod2），則f（vi，jvi+1，j）=15，若j≡0（mod2），則f（vi，jvi+1，j）=16；當i≡2（mod3）時，若j≡1（mod2），則f（vi，jvi+1，j）=17，若j≡0（mod2），則f（vi，jvi+1，j）=18；當i≡0（mod3）時，若j≡1（mod2），則f（vi，jvi+1，j）=19，若j≡0（mod2），則f（vi，jvi+1，j）=20.

（3）在 E3上：設 j≡k（mod7）.當 i≡1（mod7）時，若k=1、2、3、4、5、6，則f（vi，jvi+1，j+1）=2k-1，若k=0，則f（vi，jvi+1，j+1）=13；當i≡2（mod7）時，若k=1、2、3，則f（vi，jvi+1，j+1）=2k+7，若k=4、5、6，則f（vi，jvi+1，j+1）=2k-7，若k=0，則f（vi，jvi+1，j+1）=7；當i≡3（mod7）時，若k=1、2、3、4、5、6，則f（vi，jvi+1，j+1）=2k+1，若k=0，則f（vi，jvi+1，j+1）=1；當i≡4（mod7）時，若k=1、2，則f（vi，jvi+1，j+1）=2k+9，若k=3、4、5、6，則f（vi，jvi+1，j+1）=2k-5，若k=0，則f（vi，jvi+1，j+1）=9；當i≡5（mod7）時，若k=1、2、3、4、5，則f（vi，jvi+1，j+1）=2k+3，若k=6，則f（vi，jvi+1，j+1）=1，若k=0，則f（vi，jvi+1，j+1）=3；當i≡6（mod7）時，若k=1，則f（vi，jvi+1，j+1）=13，若k=2、3、4、5、6，則f（vi，jvi+1，j+1）=2k-3，若k=0，則f（vi，jvi+1，j+1）=11；當i≡0（mod7）時，若k=1、2、3、4，則f（vi，jvi+1，j+1）=2k+5，若k=5、6，則f（vi，jvi+1，j+1）=2k-9，若k=0，則f（vi，jvi+1，j+1）=5.

（4）在 E4上：設 j≡k（mod7）.當 i≡1（mod7）時，若k=1、2、3、4、5、6，則f（vi+1，jvi，j+1）=2k，若k=0，則f（vi+1，jvi，j+1）=14；當i≡2（mod7）時，若k=1、2、3、4，則f（vi+1，jvi，j+1）=2k+6，若k=5、6，則f（vi+1，jvi，j+1）=2k-8，若k=0，則f（vi+1，jvi，j+1）=6；當i≡3（mod7）時，若k=1，則f（vi+1，jvi，j+1）=14，若k=2、3、4、5、6，則f（vi+1，jvi，j+1）=2k-2，若k=0，則f（vi+1，jvi，j+1）=12；當i≡4（mod7）時，若k=1、2、3、4、5，則f（vi+1，jvi，j+1）=2k+4，若k=6，則f（vi+1，jvi，j+1）=2，若k=0，則f（vi+1，jvi，j+1）=4；當i≡5（mod7）時，若k=1、2，則f（vi+1，jvi，j+1）=2k+10，若k=3、4、5、6，則f（vi+1，jvi，j+1）=2k-4，若k=0，則f（vi+1，jvi，j+1）=10；當i≡6（mod7）時，若k=1、2、3、4、5、6，則f（vi+1，jvi，j+1）=2k+2，若k=0，則f（vi+1，jvi，j+1）=2；當i≡0（mod7）時，若k=1、2、3，則f（vi+1，jvi，j+1）=2k+8，若k=4、5、6，則f（vi+1，jvi，j+1）=2k-6，若k=0，則f（vi+1，jvi，j+1）=8.

圖P10P10在f之下的邊染色如圖7所示，不難驗證f是一個強邊染色.綜上有χS′（PmPn）≤26.故χS′（PmPn）=26.

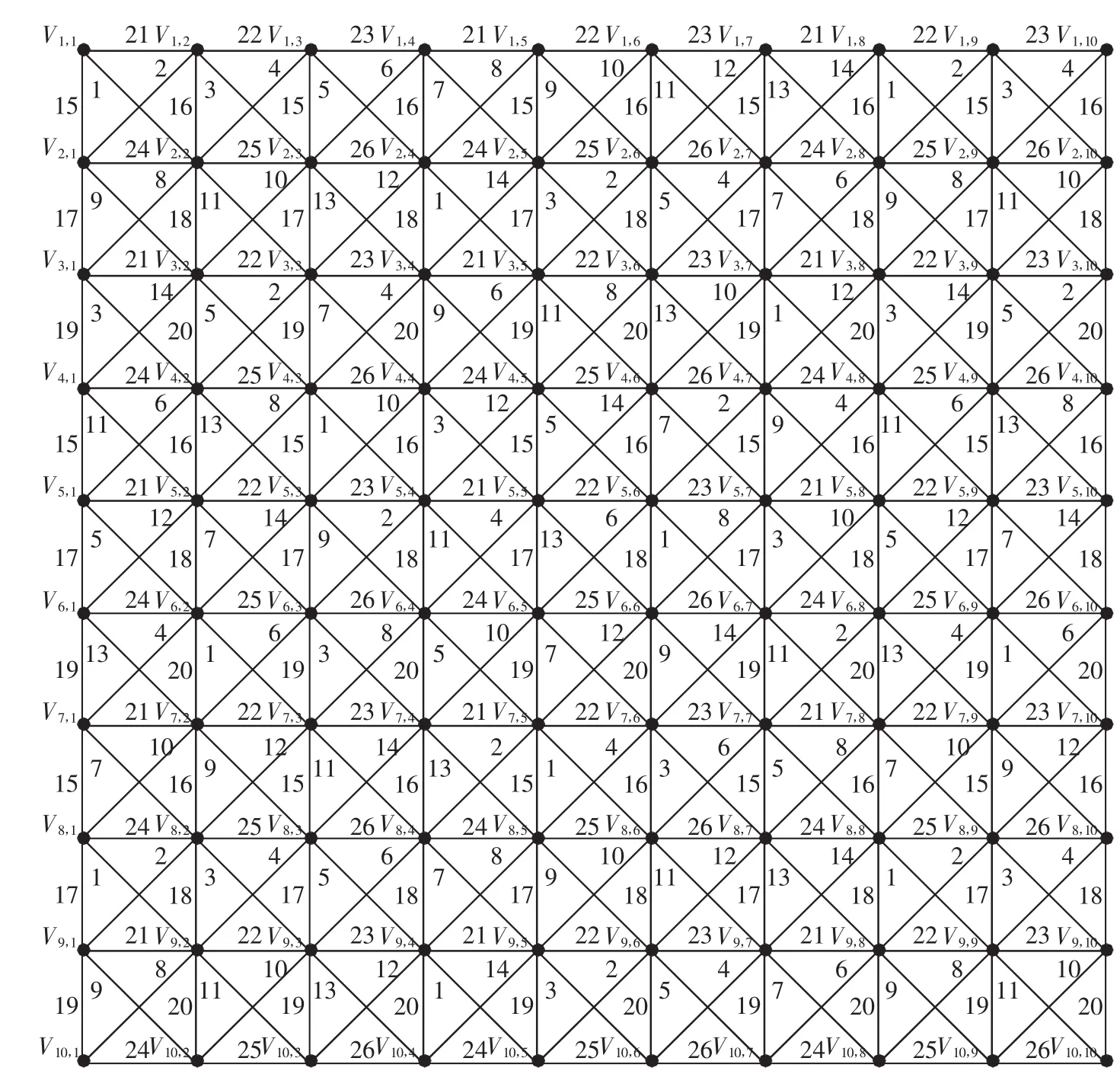
圖7 圖P10P10的強邊染色Fig.7 Strong edge-coloring of P10P10