導彈突防概率解析與仿真計算結果差異分析

胡振震，王亮，楊寶慶，胡玉理，楊文

(中國洛陽電子裝備試驗中心，河南 洛陽 471000)

0 引言

彈道導彈突防概率計算[1-3]主要有2種方法： 一是解析計算；二是仿真計算。解析計算主要基于概率論等構建導彈突防概率解析計算表達式[4-9]。仿真計算通常利用蒙特卡羅方法構建突防仿真模型[10-13]。一般情況下2種方法得到的計算結果是一致的，但一些情況特別是攻擊彈頭略飽和(攔截彈數量略不足) 時，兩者會存在明顯的差異。

考慮一個簡單的算例(a): 真實攻擊彈頭數w=10，重誘餌數α=0，輕誘餌數β=0，彈頭可靠性PR=1.0，發現概率PD=0.9，跟蹤概率PT=1.0，識別概率PI=1.0，攔截彈數量N=9，1枚彈頭需求攔截彈數n=1，攔截彈可靠性Pr=1.0。分析這些數據很容易得到解析計算結果，攔截概率為1，攔截彈可靠性為1，彈頭的跟蹤識別概率都為1，彈頭的可靠性為1，那么彈頭都可靠且發現1枚就能攔截1枚，因為發現概率是0.9，那么能夠發現9枚同時也能攔截9枚，即突防彈頭是1枚，突防概率是0.1，然而仿真計算結果為突防彈頭數1.349，突防概率為0.135。這2種方法哪一種是正確的，實際應用時應該采用哪一種方法的結果作為參考，這是決策者很關心的問題，也是本文需要解決的問題。

1 各階段統一的解析和仿真計算模型

彈道導彈突破反導系統[14]的各個階段(初、中、末段)可以用統一模型進行計算，各階段的差異僅在于輸入參數的不同(比如:彈頭和誘餌是否分離，攔截策略等)。反導系統各階段都可分預警和攔截[15]過程，預警過程主要有發現、跟蹤、識別環節，計算需考慮發現概率、跟蹤概率、識別概率，而攔截過程主要有攔截環節，需考慮攔截(或毀傷)概率。對于某一階段的突防過程，假設有w個真實彈頭和α個重誘餌，β個輕誘餌，彈頭可靠性為PR，攔截彈的數量為N，可靠性為Pr。真實彈頭的發現、跟蹤、識別、攔截概率分別為PDw，PTw，PIw，PKw。重誘餌的發現、跟蹤、識別、攔截概率分別為PDα，PTα，PIα，PKα。輕誘餌的發現、跟蹤、識別、攔截概率分別為PDβ，PTβ，PIβ，PKβ。

1.1 解析計算模型

突防過程首先考慮發現和跟蹤環節，則彈頭和誘餌被發現和跟蹤的數量為

wPRPDwPTw+αPRPDαPTα+βPRPDβPTβ.

考慮識別環節，彈頭被識別為真彈頭的概率為PIw，重/輕誘餌識別為彈頭的概率PIα,PIβ，則彈頭和誘餌識別為真彈頭的總數(即需攔截的總彈頭數)為

A=Aw+Aα+Aβ=wPRPDwPTwPIw+

αPRPDαPTαPIα+βPRPDβPTβPIβ.

考慮攔截環節，采用n攔1策略(即n枚攔截彈攔截1枚彈頭，n枚攔截彈攔截1枚彈頭的過程視為泊松流過程)。當nA≤N時，即攔截彈數量能滿足n攔1的需求，被攔截的彈頭和誘餌數量為

Aw[1-(1-PrPKw)n]+Aα[1-(1-PrPKα)n]+
Aβ[1-(1-PrPKβ)n].

當nA>N時，即攔截彈數量不足時，被攔截的彈頭和誘餌數量為

因為考慮到誘餌和真實彈頭都已被識別為真實彈頭，不分彼此，所以攔截彈N/n對于彈頭和誘餌來說是平均分配的，不考慮彈頭和誘餌的不同導向概率[16]，其比率為Aw∶Aα∶Aβ。因此，當nA≤N時，突防的真實彈頭數為

wPR{1-PDwPTwPIw[1-(1-PrPKw)n]}.

當nA>N時，突防的真實彈頭數為

總結起來，n攔1策略導彈突防概率的解析計算模型為

(1)

1.2 蒙特卡羅仿真模型

利用蒙特卡羅方法進行仿真實驗，突防的彈頭數量是最終的樣本期望，樣本則是一次突防實驗的結果。樣本值認為是一些隨機變量的函數，這些隨機變量則是定義在多個不同的事件空間上的實函數，具有某一概率密度[17]。直接影響突防彈頭數量的事件包括彈頭可靠性事件和彈頭被攔截事件，而被攔截事件又與發現事件/跟蹤事件/識別事件相關，還與攔截方的攔截彈數量和攔截策略有關，也與攔截的是否為誘餌有關，因為被攔截的可能是被識別為彈頭的誘餌，因而需考慮彈頭類型事件。

真實彈頭(或者攔截彈)可靠性事件是一個隨機二值事件，要么可靠，要么不可靠，依概率收斂于期望。可靠性函數hr為隨機變量xr的函數。即:

類似還存在: 彈頭發現事件的函數hdw為隨機變量xdw的函數，彈頭跟蹤事件的函數htw為隨機變量xtw的函數，彈頭識別事件的函數hiw為隨機變量xiw的函數，一枚真實彈頭被一枚攔截彈攔截的事件的函數hkwone為隨機變量xkw的函數，彈頭類型事件的函數htpw為隨機變量xtp的函數等。重誘餌和輕誘餌也存在與上述彈頭事件類似的事件。

突防概率有2種仿真方式：一種是對發射的所有彈頭在突防各環節進行整體處理，即齊射式的仿真；第2種是對發射的所有彈頭逐個進行完整突防過程處理，即順序式的仿真。下面分別給出仿真框架:

考慮齊射式攔截，發現、跟蹤、識別、攔截每一個環節都需要對所有彈頭進行整體處理，處理完一個環節后再處理下一個環節。一次仿真過程包括步驟如下:

(1) 首先考慮可靠性事件，經可靠性處理后原有彈頭w，α，β中可靠的彈頭數為m1w,m1h,m1l。

(2) 接著考慮發現、跟蹤、識別事件(即處理發現、跟蹤、識別環節)，處理后得到成功識別的彈頭數為m2w,m2h,m2l。

(3) 接著考慮攔截事件(即處理攔截環節)，分2種情況：當m2n≤N(m2=m2w+m2h+m2l)時，攔截彈足夠；當m2n>N時，攔截彈不足，需考慮彈頭類型事件。得到被攔截的彈頭數為m3w,m3h,m3l。

(4) 最后得到n攔1策略的突防真實彈頭數hw=m1w-m3w。

考慮順序式攔截，總的突防彈頭數由各枚突防彈頭累加得到。當一枚彈頭是真實彈頭，可靠且沒有被攔截，則該枚彈頭實現突防。那么突防的真實彈頭總數為

(2)

式中:x為識別為彈頭的真實彈頭數量;y，z為識別為彈頭的重誘餌，輕誘餌的數量；htpwi為彈頭類型函數。

根據n攔1策略，彈頭被攔截事件的函數hki與可靠性函數、發現函數、跟蹤函數、識別函數、單枚攔截彈的攔截函數和可靠性函數，以及攔截彈存在函數有關(max函數描述n攔1策略下n枚攔截彈只需其中有1枚實現攔住即可):

hki=max{hkwonejhrdfj,j=1,n}f(Ni).

(3)

而xd為未經攔截過程直接突防的真實彈頭數，與x，y，z取值有關:

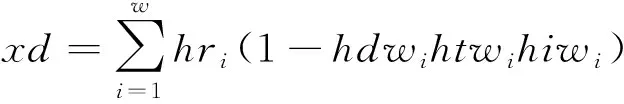
(4)

攔截彈存在函數f為

式中:Ni表示攔截第i枚彈頭前所剩余的攔截彈數量。剩余的攔截彈數與識別為彈頭事件的二值函數hisw相關，它是隨機變量xtp和彈頭、誘餌的發現、跟蹤、識別事件的函數。

2 解析和仿真計算結果差異分析

2.1 預警和攔截過程的非獨立性影響

考慮前述算例(a)，根據式(1)計算得到突防概率為0.1。而仿真計算無論是齊射式仿真還是順序式仿真結果都是0.135。在齊射式仿真中，總彈頭10枚，因為可靠性為1.0,那么10枚彈頭都可靠。對于發現概率0.9，因為發現事件是隨機的，那么在一次實驗中的發現彈頭數可能是9，也可能是其他值，而樣本集的均值能依概率收斂于9，但是對于單個樣本(單次實驗得到的結果)來說，其值不一定是9，也有可能是10,8,7，又因為攔截概率為1，攔截彈數為9，那么最多能攔截的彈頭數是9枚，所以可能被攔截的彈頭數會是9,8,7，而不可能是10，于是攔截過程會帶通地把所有發現彈頭數大于9的隨機事件排除，那么對于樣本集來說，發現彈頭數為10的情況相當于僅發現9枚的情況，因此攔截彈不足(即攻擊彈頭的飽和)導致的結果相當于發現彈頭數無法依概率收斂到9。說明攻擊彈頭飽和(當攔截彈不足)時，發現事件與攔截事件是相關的，而不是獨立的。

在順序式仿真中，總彈頭數10枚，對于第1枚彈頭，必然可靠，可能被發現也可能不被發現，被發現后消耗一枚攔截彈并確定被攔截，第2～9枚彈頭類似，可能被發現也可能不被發現，發現即被攔截，但對于第10枚彈頭來說，發現了也可能不被攔截，如果前面攔截彈已經使用完了，那么自然就無法攔截。因此被攔截的彈頭數量最大只能是9，而且一定會存在小于9的情況，因為隨機發現事件必然會出現發現彈頭數小于9比如8，7等情況，因此被攔截彈頭數的期望必然會小于9，突防彈頭數必然大于1。同樣說明了發現事件與攔截事件的非獨立性。

而對于解析計算來說，發現事件和攔截事件是確定獨立的，發現概率是0.9，那么解析計算一定是發現9枚彈頭，并且因為攔截概率等于1，解析計算也一定是9枚彈頭被攔截，剩下1枚彈頭突防。

上述分析表明，預警過程發現環節的事件與攔截過程的事件間的非獨立性會導致仿真結果與解析計算結果的差異，同樣可以推論: 跟蹤、識別等與發現環節性質類似的事件也會帶來相同影響。

2.2 算例分析

仍然利用算例(a)來分析預警和攔截過程各環節的獨立性。圖1給出了攔截彈可靠性為0.9，其他概率為1時的突防概率，橫軸為攔截彈數量，縱軸為突防概率。隨著攔截彈頭數增加，突防概率逐漸下降到0.1，當攔截彈數量達到10后，突防概率維持0.1不變，因為所有的彈頭均已攔截，剩余的攔截彈不再使用。解析計算、齊射式仿真、順序式仿真三者結果完全一致，根據解析計算的獨立性，說明當攔截彈可靠性為0.9，其他概率為1.0時，預警和攔截過程各個環節是獨立的。圖2給出了攔截彈可靠性為0.9，攔截概率為0.9，其他概率為1時的突防概率，其結果與圖1類似，說明攔截彈可靠性和攔截概率的變化不影響各環節的獨立性。

圖1 突防概率(Pr=0.9)Fig.1 Penetration probability(Pr=0.9)

圖2 突防概率(Pr=0.9,PK=0.9)Fig.2 Penetration probability(Pr=0.9,PK=0.9)

圖3給出了攔截彈可靠性為0.9，攔截概率為0.9，彈頭可靠性為0.9，其他概率為1時的突防概率，圖中在攔截彈數為9時，仿真結果和解析計算結果存在明顯差異，當攔截彈數為8時存在細微的差異。說明攻擊彈頭略飽和時彈頭可靠性影響了各環節的獨立性。圖4給出了攔截彈可靠性為0.9，攔截概率為0.9，彈頭識別概率為0.9，其他概率為1時的突防概率，其結果與圖3類似，說明識別概率也帶來相同的影響。因為發現、跟蹤與識別環節的性質類似，可以推論發現、跟蹤概率也將產生同樣的影響。

圖3 突防概率(Pr=0.9,PK=0.9,PR=0.9)Fig.3 Penetration probability(Pr=0.9,PK=0.9,PR=0.9)

圖4 突防概率(Pr=0.9,PK=0.9,PI=0.9)Fig.4 Penetration probability(Pr=0.9,PK=0.9,PI=0.9)

圖5給出了彈頭識別概率為0.9，其他概率為1.0時的突防概率，進一步驗證識別概率會影響獨立性，而攔截概率和攔截彈的可靠性則不會。總的來說：當攻擊彈頭略飽和時，彈頭的可靠性、發現概率、跟蹤概率、識別概率對預警和攔截過程各環節的獨立性存在影響，而攔截概率和攔截彈可靠性則沒有。

圖5 突防概率(PI=0.9)Fig.5 Penetration probability(PI=0.9)

2.3 數學驗證

從上述算例可知，當PR，PD，PT，PI存在小于1的情況時，仿真和解析計算差異主要發生在N=n(A-1)附近，即攻擊彈頭略飽和(攔截彈頭略不足)時。利用一個更為簡化的算例(b)來對順序式仿真進行數學分析，考慮彈頭數w=3，誘餌數為0，PD=0.9，其他概率值都等于1，n=1，那么式(2)，(3)可以改寫為

(5)

進一步展開為

hw= 1-hdw1f(N)+1-hdw2f(N-hdw1)+

1-hdw3f(N-hdw1-hdw2).

(6)

計算得到A=2.7，即當攔截彈數N=A-1=1.7附近會存在差異，因此考慮計算攔截彈數N為1～4的情況進行分析。當N=4時，hw的數學期望(均值)為

E(hw)= 1-E(hdw1f(4))+1-E(hdw2f(4-

hdw1))+1-E(hdw3f(4-hdw1-hdw2)).

因為4≥1,4-hdw1≥1,4-hdw1-hdw2≥1;

所以E(hw)=1-E(hdw1)+1-E(hdw2)+1-E(hdw3),

E(hw)=1-PD+1-PD+1-PD=0.3,

P=E(hw)/w=0.1.

該結果與式(1)的結果一致。

當N=3時，得到類似的結果:

E(hw)= 1-E(hdw1f(3))+1-E(hdw2f(3-

hdw1))+1-E(hdw3f(3-hdw1-hdw2))·

因為3≥1,3-hdw1≥1,3-hdw1-hdw2≥1;

所以E(hw)= 1-E(hdw1)+1-

E(hdw2)+1-E(hdw3),

E(hw)=1-PD+1-PD+1-PD=0.3,

P=E(hw)/w=0.1.

當N=2時，情況有所不同:

E(hw)= 1-E(hdw1f(2))+1-E(hdw2f(2-

hdw1))+1-E(hdw3f(2-hdw1-hdw2)),

因為2≥1,2-hdw1≥1,2-hdw1-hdw2?≥1.

因為f的參數值與hdw相關，不全大于1，所以求期望時可利用全概率公式計算:

P(hdw1= 1,hdw2=1)E(hw)=

0.81×(1-1+1-1+1-0)=0.81;

P(hdw1= 1,hdw2=0)E(hw)=

0.09×(1-1+1-0+1-0.9)=0.099;

P(hdw1= 0,hdw2=1)E(hw)=

0.09×(1-0+1-1+1-0.9)=0.099;

P(hdw1= 0,hdw2=0)E(hw)=

0.01×(1-0+1-0+1-0.9)=0.021;

E(hw)=1.029;

P=E(hw)/w=0.343.

當N=1時，也有:

E(hw)= 1-E(hdw1f(1))+1-E(hdw2f(1-hdw1))+

1-E(hdw3f(1-hdw1-hdw2))，

1≥1,1-hdw1?≥1,1-hdw1-hdw2?≥1；

P(hdw1=1,hdw2=1)E(hw)=
0.81×(1-1+1-0+1-0)=1.62；
P(hdw1=1,hdw2=0)E(hw)=
0.09×(1-1+1-0+1-0)=0.18；
P(hdw1=0,hdw2=1)E(hw)=
0.09×(1-0+1-1+1-0)=0.18；
P(hdw1=0,hdw2=0)E(hw)=
0.01×(1-0+1-0+1-0.9)=0.021；
E(hw)=2.001；
P=E(hw)/w=0.667.

從式(1)計算得到N=2，N=1時的P為

P(N=2)=0.333 333 333，
P(N=1)=0.666 666 666.

說明當N=2時，兩者差異明顯;N=1時，兩者有略微的差異。

從結果看，因為仿真過程是1枚接1枚的攔截，所以前面處理的彈頭是否發射攔截彈會影響后面彈頭的攔截，這可能會構成一種條件概率。當攻擊彈頭數不飽和時(即攔截彈足夠多，比如N≥nA時)，無論前面攔截過程是什么情況，后面的攔截彈頭都足夠，這樣識別事件和攔截事件互相獨立，那么期望計算不考慮條件概率。但在攻擊彈頭數略飽和時(即攔截彈數量略少于需求攔截彈數，比如N=n(A-1)時)，前面彈頭的攔截情況使得后面彈頭面臨的攔截彈有可能足夠，也有可能不足，這就導致期望值處于攔截彈足夠和不足2種情況之間，計算需要考慮條件概率，這進一步體現了此時預警和攔截過程各個環節的非獨立性。相比之下，在解析計算中攔截彈不足就是不足，因為各環節是互相獨立的，其期望無需考慮條件概率。仿真計算和解析計算的差異就在于此，這也說明仿真計算能夠考慮預警和攔截過程各環節互相影響的事實。

3 結束語

本文建立了彈道導彈突防各階段統一的解析計算和蒙特卡羅仿真計算模型，通過算例比較，分析了攻擊彈頭略飽和時2種模型計算結果的差異，得出結論如下: 當攻擊彈頭數不飽和(即攔截彈數量足夠時)，預警和攔截過程的各個環節是獨立的，解析計算和仿真計算結果一致，但是當攻擊彈頭數飽和時，各環節不再具有獨立性，這導致了解析計算和仿真計算結果的差異。在實際應用中，因為仿真計算模型能考慮到各環節非獨立性問題，所以更接近真實情況，從結果正確性角度考慮，決策者應以仿真結果作為參考依據。