初中數學概念類問題教學研究

俞雪強

[摘 要] 初中數學概念是初中數學知識的基礎，是整個數學知識體系的重要組成部分，是開展初中數學教學的必要保障. 因此，分析初中數學概念的特點，分析初中數學概念的學習過程，對于提高初中數學概念類問題的教學而言，具有重要的意義.

[關鍵詞] 初中數學；概念；教學研究

數學概念是初中數學的基礎，是整個數學知識體系的重要組成部分，只有將數學概念掌握好，才能理解數學問題，推導數學公式，應用數學知識. 傳統教學模式下的概念教學存在許多問題，這些問題嚴重阻礙了學生對概念的學習. 因此，研究數學概念教學的意義重大.

初中數學概念的特點

數學概念是人腦對客觀事物中數量關系和空間形式的反應，它具有較強的抽象性和層次性. 它雖然是對現實生活中部分問題的反應，但是它反應的是事物最為本質的特點，具有較強的概括性和簡潔性. 因此，人們對概念的理解具有較強的抽象性. 數學概念反映的問題均來源于現實生活，通過現實生活都可以找到它的原型，因此，數學概念又與我們的生活密切相關，具有一定的具體性. 數學概念還有一個特點，即具有一定的層次性. 在對初中數學教材中的數學概念進行整理時會發現，在多達幾百個的數學概念中，這些概念并不雜亂，而是具有一定的層次性. 例如，在數的概念下分支出實數的概念，接下來又分支出有理數和無理數的概念，在有理數概念下又可以分支出整數和分數的概念. 另外，這些概念之間還存在一定的聯系，并不是獨立存在的. 例如，在單項式和多項式的概念中，多項式就是由單項式推出來的；在方程、函數、不等式的學習中，也是借助一種概念去理解另一種概念，通過這種概念之間的聯系，能夠促進知識之間的遷移，幫助學生形成知識網絡. 通過概念之間的聯系，能使概念自身具有一定的發展性. 例如，根據教材上的安排，數學中的知識是由“單項式—多項式—整式”“方程—函數—不等式”逐漸發展過渡的.

數學概念的學習過程

數學概念的學習主要包括以下四個環節：引入、理解、鞏固、建構體系，其中，概念的引入很大程度上決定了概念學習的效果，就像俗話說的那樣，“良好的開端是成功的一半”. 在數學概念教學過程中，良好的引入環節能夠激發學生學習數學概念的興趣，能幫助學生加深對相關概念的理解. 而不恰當的概念引入，不僅不利于學生對概念的理解，還會讓學生感覺枯燥乏味，最終失去概念學習的興趣. 引入概念以后，學生需要對相關概念加以理解，把握概念中最為本質的內涵，這是概念學習的中心環節. 學生只有理解了相關概念的本質內涵，才能在接下來的學習中正確區分相關知識，并順利進行后續學習. 學生理解概念以后，還需要借助相關的練習來進行鞏固，進一步加深對相關概念的理解，否則，非常容易出現記憶不準確、理解不到位和運用不靈活的情況，甚至會出現跟以前所學習的知識混淆的情況，最終阻礙今后的數學學習. 因此，鞏固數學概念非常重要. 最后的階段就是概念知識體系的建構階段，通過這一環節，學生能夠將新學習的概念與之前學習的概念建立聯系，再次遇到相似概念時能及時加以區分，并能準確選擇概念加以運用. 經過這四個環節的學習過程，才算是真正完成了概念的學習.

初中數學概念學習策略

1. 概念的引入階段

概念引入階段的效果直接影響著概念教學的成敗，因此，在引入數學概念的時候不僅要考慮知識的結構，還要照顧到學生的學習特點，這樣才能在概念的引入階段激起學生的學習欲望.

首先，在概念引入階段，我們可以借助生活實例來引入相關數學概念. 初中階段的學生抽象思維能力還不夠強，我們可以借助身邊一些熟悉的具體事物和一些具有代表性的事例幫助學生建立概念表象. 例如，學習平行四邊形時，教師可以引入學校門口的伸縮門，院墻四周的籬笆，通過觀察它們的形狀尋找共同點，然后引入平行四邊形的概念. 這樣，學生不僅能形象地感知這一概念，還能理解數學源于生活的含義，能提高學生利用所學知識解決現實生活中的問題的能力.

其次，我們可以通過游戲、實驗、調查等“活動”的方式引入相關概念，通過一定的活動，讓學生自主發現，這正好符合初中階段學生的心理，尤其是低年級的學生，他們的注意力不夠集中，通過活動的形式能取得更好的教學效果. 例如，引入對稱軸的相關概念時，可以通過一個小游戲來實現：將一張白紙進行對折，之后沿著中間的折線剪一任意圖形，然后展開紙張會發現，剪出的圖形沿著折線，兩側能夠完全重合，然后再引出軸對稱圖形和軸對稱的概念. 在這個活動中，學生通過自己動手發現了問題、總結了問題，極大地提高了學習的積極性，同時也加深了印象.

第三，借助問題，讓學生腦海中產生認知沖突，激發學生的求知欲望，在學生渴望探究新知識的過程中引入概念. 例如，學習“圓”的概念時，教師可以提問：為什么車輪是圓形，而不是三角形呢？通過這樣的問題，讓學生主動探究，在不斷的知識探究中得到圓的概念.

最后，通過類比的方式來引入. 我們都知道，初中數學中的很多概念不是孤立存在的，它們之間存在著密切的聯系，于是我們可以借助已經學過的一種概念來引出將要學習的新概念. 通過這種由一種事物推測另一種事物的方式來完成概念的引入. 例如，引入分式的概念時，可以首先引入學生較為熟悉的分數，讓學生比較分式與分數的異同，然后給出多組式子，總結分式的概念. 從學生熟悉的概念入手，循序漸進，能降低學習難度.

2. 概念的理解階段

首先，可以借助正、反例子來幫助學生理解. 借助正例能夠幫助學生更加清晰地理解概念的本質，對學生原有的概念認識起到一定的強化作用. 例如，學習了多項式的概念后，可列舉出a+b，a-b，a2+ab+1等多項式加深學生的理解. 另外，借助反例能夠幫助學生選出其他相似概念的干擾，起到定向糾錯的效果. 例如，學習“數軸”的概念后，讓學生觀察下列數軸，幫助學生理清概念.

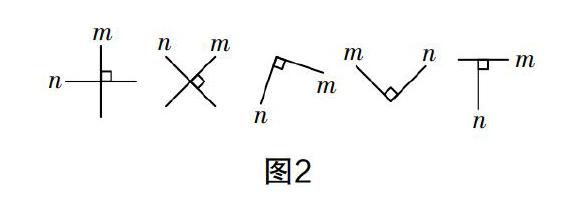
其次，進行變式訓練. 即在本質不變的情況下，改變它的表現形式，讓學生能夠更加準確地把握數學概念. 例如，學習垂直概念時，我們可以通過圖形變式的方式來讓學生加深對概念本質的理解，即通過觀察圖2中的圖形進一步認識垂直這一概念.

第三，借助現代信息技術輔助教學. 學生在學習數學概念時，都是從具體的感性認識向抽象的理性認識逐漸過渡的，借助現代信息技術，能夠將抽象的問題以具體的圖像的方式展示出來，輔助學生理解. 例如，學習“直線與圓的位置關系”的相關知識時，就可以利用幾何畫板模擬位置關系，這一形象的概念就會留在學生的印象當中.

3. 概念的鞏固階段

概念理解的基礎是先記住它. 由于學生對概念學習的積極性并不高，所以需要通過多樣的方式去完成記憶. 因此，教師可以讓學生采取復述的方式加深記憶，讓學生利用自己的語言對相關概念進行復述. 并且，可以將這種復述方式貫穿整堂課. 例如，上課之前，可以先對上節課學習的概念進行復述，課堂上又可以對新學習的概念進行復述，在這樣不斷的復述下，學生對相關概念的理解就會變得更加透徹.

鞏固概念的一個重要途徑就是練習. 通過適度練習，學生能夠把握概念的一些細節，能夠給學生提供反思改進的機會. 需要注意的是，不能盲目練習，練習的內容要具有代表性，難度要適中. 例如，在絕對值概念的學習中，先就正數、負數、小數等絕對值進行練習；然后就知道絕對值求數值進行練習；最后，通過數軸觀察絕對值.

4. 概念的知識體系建構階段

隨著數學的學習，數學概念會不斷增加，因此，要引導學生建立概念之間的聯系，將它們體系化，這樣不僅有利于學生把握知識，還有助于知識的遷移. 例如，學生學習了平行四邊形后，又學習了菱形、正方形，教師要引導學生做好概念的梳理，讓學生對初中數學概念體系有一個清晰的把握.