一種基于互相關系數的白噪聲不相關性檢驗方法
白春樂,馬 嬌
(1.西安郵電大學計算機學院, 陜西 西安 710121) (2.愛立信(西安)信息通信技術服務有限公司,陜西 西安 710077)
在對雷達系統設計、仿真和信號處理算法性能進行評估時不僅需要產生雜波,而且需要所模擬的雜波具有指定的統計特性,因此需要對模擬的雜波進行概率密度函數(probability density function, PDF)和功率譜密度(power spectrum density, PSD)的檢驗,以確定所產生的雜波是否滿足要求。這也是各種雜波模擬算法能否得到實際應用的前提。
目前雜波PDF的檢驗方法較為成熟,對于白噪聲的不相關性,主要有正態性檢驗、χ2檢驗及部分序列值的相關性檢驗、T統計量檢驗等檢驗方法,這些方法都依據假設檢驗的思想,即先提出統計假設,構造某一符合特定分布的統計量,給定顯著性水平,查該分布的臨界值表得到統計量的上限臨界值,根據計算出的統計量與臨界值的關系判斷是否接受原假設。
正態性檢驗基于Bartlett公式[1],檢驗統計量服從正態分布。該方法的限制條件十分嚴格,自相關系數序列的每個序列值都要被檢驗。由于白噪聲序列的隨機性,可能有一些檢驗統計量的值超出給定的顯著性水平下的臨界值,但只要這些值出現的概率不超過顯著性水平即可。眾所周知,標準正態分布的變量的平方和服從χ2分布[2-3]。因此,基于雜波PDF的正態性檢驗,可以檢驗其統計量的平方和是否服從χ2分布。但該方法只有一個檢驗統計量,缺乏對不同時移值下不相關性的判斷,且檢驗條件比較模糊,可能導致檢驗結果不準確。
本文對兩個隨機序列互相關性檢驗的方法進行了改進,用于白噪聲序列的自相關性檢驗,并進行了仿真研究。結果表明,該方法有效地消除了上述白噪聲不相關性檢驗的正態性檢驗和χ2檢驗方法的局限性,可以廣泛使用。
1 算法原理
對于隨機序列x(n)和y(n),其互相關系數可用下式進行估計[4]:
(1)
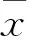
根據Fisher的Z變換理論[6],如果兩個序列的自相關系數不是正態分布的,那么可以通過式(2)將其轉化為服從正態分布的變量w:
(2)
w的期望為:
(3)
式中:ρxy為互相關系數的實際值。
方差為:
(4)
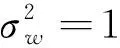
(5)
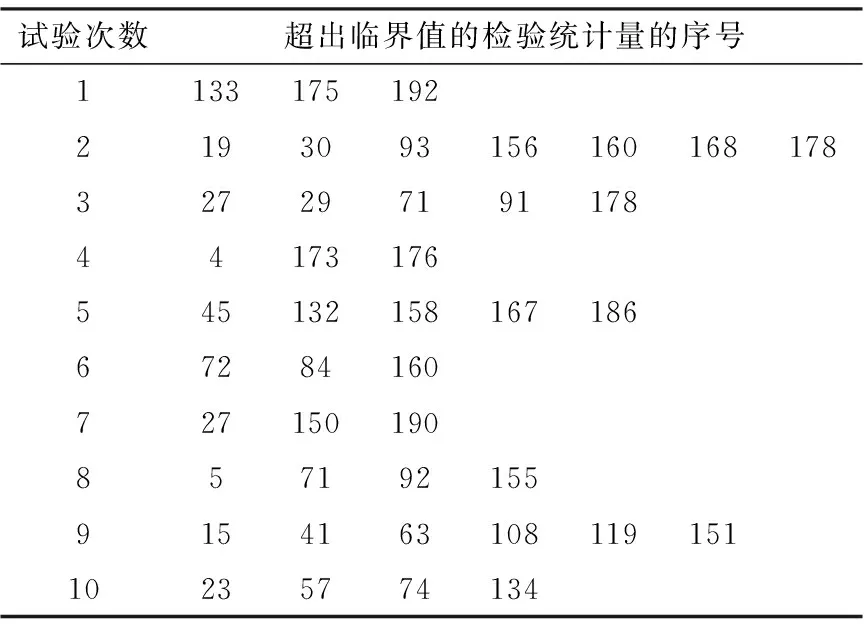
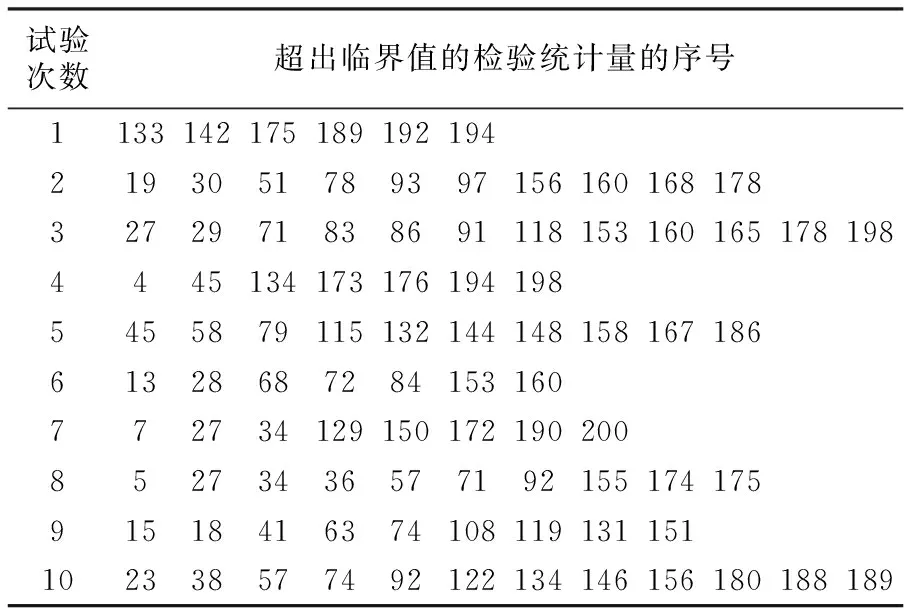
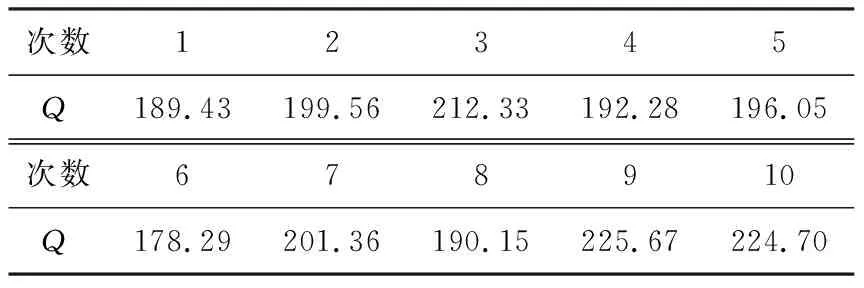
給定顯著性水平α,臨界值zα/2可以通過查標準正態分布表得到。如果|z| 對于一個白噪聲序列u(n),若令x(n)=u(n),y(n)=u(n+m),m為相對于n時刻的時移值,則式(1)可轉化為白噪聲的自相關系數,即: (6) (7) 該檢驗統計量可用作白噪聲的不相關性檢驗。 表1 基于互相關系數的白噪聲 由表1可知,上述方法中超出臨界值的檢驗統計量所占的百分比最大值為7/200=3.5%<5%[1],因此空假設可以被接受,即在顯著性水平α=5%的條件下,白噪聲序列u(n)不相關。 下面將上述方法與已有的正態性檢驗、χ2檢驗進行比較。 (8) 因此正態性檢驗的檢驗統計量可定義為: (9) 表2 正態性檢驗試驗結果 從表中可以看出,超出臨界值的檢驗統計量所占的百分比最大值為12/600=6%,與小于5%的要求相差不大,可以認為在5%的顯著性水平下,產生的隨機序列是白噪聲序列。 由表1和表2可知,在相同的顯著性水平下,正態性檢驗中超出臨界值的檢驗統計量所占的百分比大于基于互相關函數的檢驗方法中的該值,并且表1中的序號都可以在表2中找到,因此相比于正態性檢驗法,基于互相關函數的白噪聲的不相關性檢驗方法更精確。 因此檢驗統計量Q可以定義為: Q服從自由度為L的χ2分布。 表3 檢驗結果表 χ2檢驗法是一種全局檢驗方法,其中的檢驗統計量是正態檢驗法中檢驗統計量的和。該方法不需要對自相關系數序列的每一點都進行檢驗,因此與前兩種方法相比更方便,檢驗標準更明確,但該方法不能對不同時移值下序列的相關性進行檢驗。 作為雷達雜波分析的重要方法,相關性檢驗算法在雷達系統的設計和仿真中至關重要。本文對互相關系數進行了改動,將其用于白噪聲的不相關性檢驗,并進行了理論分析和仿真。 通過比較可知,在相同的顯著性水平下,本文采用的方法得到的結果更精確;與χ2檢驗法相比,該方法可得到不同時移值下序列的相關性,有助于對時間點進行判斷。本文方法可以廣泛用于對白噪聲的判斷。 本文的研究更傾向于對檢驗方法的原理介紹,下一步的研究將針對該檢驗方法的實例驗證與分析展開。2 仿真研究
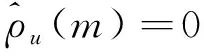
3 方法比較
3.1 正態性檢驗
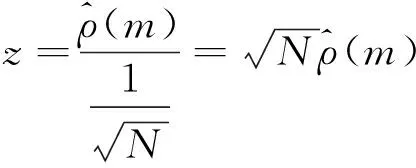
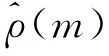
3.2 χ2檢驗
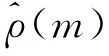
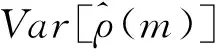
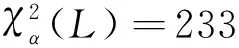
4 結束語

