基于扇形柵格模型的蟻群算法在病灶定位中的應用

徐魁伍，姚運萍

(蘭州理工大學機電工程學院, 甘肅 蘭州 730050)

探索與研究治療癌癥的先進方法對于挽救患者生命和提高患者生存質量具有重要意義；重離子治療法是一種先進的放射治療方法，具有療程短、副作用小和控制率高等優點[1]。在重離子束加速器研發成功的基礎上，重離子治癌終端設備研制是實現重離子治療癌癥的重要環節。為實現病灶定位以及治療過程中病灶與重離子束輻照的聯動[2]，需要提供安全可靠的擺位路徑，病灶擺位最優路徑規劃將為研究設備運動提供參考。文獻[3]通過方形柵格法對治療床環境進行建模，利用蟻群算法優化治療床的運動路徑。針對治療床在方形柵格中運動困難、病灶定位精度低的問題，本文利用扇形柵格法建立病灶的環境模型，利用改進的蟻群算法對該數據模型進行分析求解，以探索該模型的可行性和應用優勢。

1 構建扇形柵格環境模型

重離子束具有能量高、速度快、速度方向不易改變的特點，束流出射點的位置一旦確定就固定不變，常見的重離子束流射出方向有水平、豎直和傾斜3種情況；而激光定位儀是固定的定位輔助設備，因此治療床的運動擺位是病灶運動軌跡定位的核心問題。由于擺位過程中需要時刻追蹤病灶的空間位置，所以根據治療床的空間環境信息，利用機器人運動學中D-H參數法[4]建立4個坐標系進行病灶定位，基坐標系為{O0:x0,y0,z0}，以等中心O0為原點，以束流射線為x0軸、治療床的大回轉的豎直軸線為z0軸；第一個關節是等中心正下方大回轉的回轉中心O1；第二個關節是小回轉的回轉中心O2；第三個關節是治療床板電機輸出軸端位置O3。治療室空間如圖1所示，4個坐標系關系如圖2所示。各個關節的參數見表1。

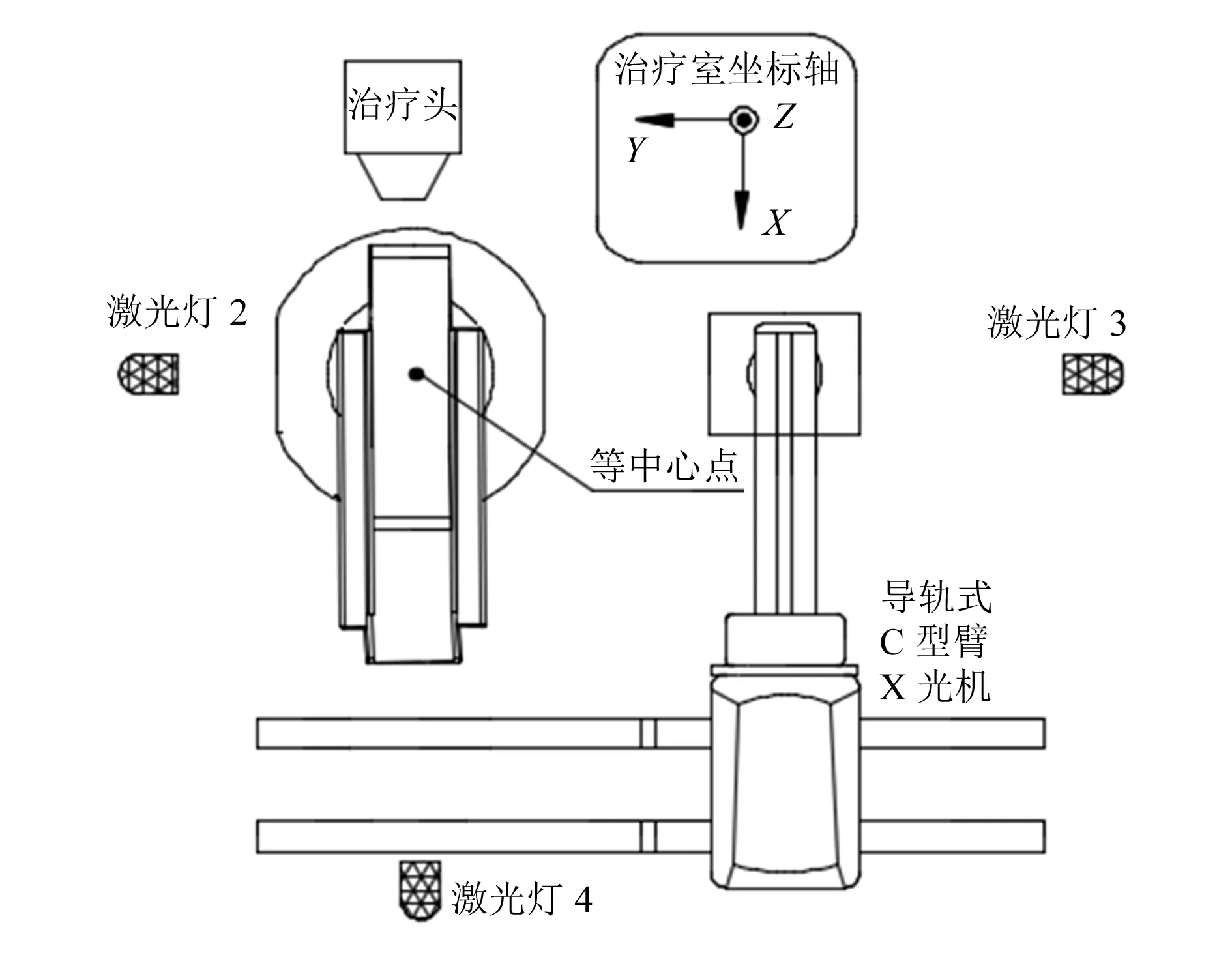
圖1 治療室空間環境簡圖

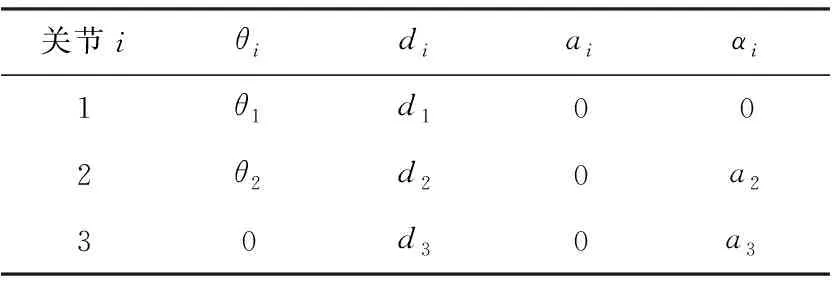
關節iθidiaiαi1θ1d1002θ2d20a230d30a3

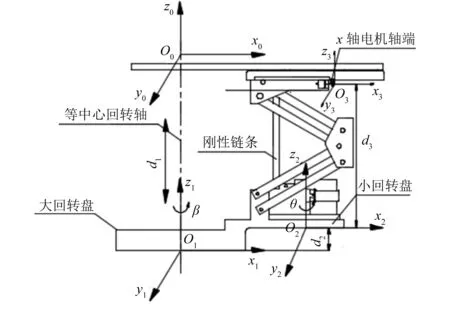
圖2 治療床D-H坐標系

各個關節的齊次矩陣為：

假定患者病灶是坐標系O3中的某一點B，記Xb(xb,yb,zb)，則病灶點B的移動矩陣為:

B點的運動方程為：

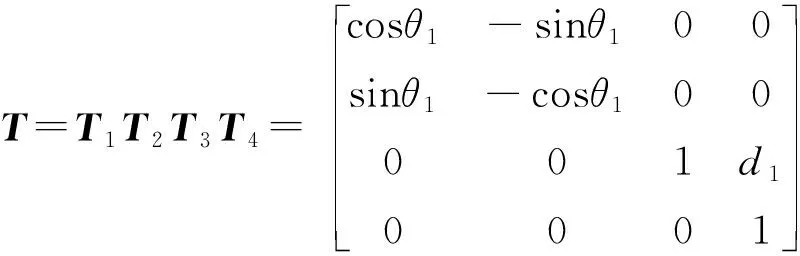
(1)

病灶點B在動坐標系{O3:x3,y3,z3}中的位置為Xb(xb,yb,zb)，通過齊次坐標變換得到其在固定坐標系{O0:x0,y0,z0}中的坐標X：

(2)

由圖2可知，d1和d2為固定值；zb為病灶在坐標系中的高度，視患者具體情況而定；d3通過剛性鏈條調節。當調節d3使得d1+d2+d3+zb=0時，則病灶在固定坐標系{O0:x0,y0,z0}的二維平面x0O0y0中，治療床的運動空間從三維空間轉化到二維空間，病灶路徑規劃問題從三維空間轉化為二維平面的路徑規劃問題。

治療室內束流輸出口、激光定位儀和C型臂X光機等障礙物的出現，以及治療床床板尺寸的影響，使得病灶在平面坐標系{O0:x0,y0}中無法完全自由運動，因此必須對病灶不能到達的位置進行標記，定義為障礙物空間，反之為自由空間。

常見的柵格劃分方法有方形柵格法、四叉樹法[5]。方形柵格法不易提高病灶的定位精度，如果提高定位精度，則格柵密度必然變大，環境信息儲量變大，抗干擾能力減弱，算法的運行時間變長；而四叉樹法通過減少柵格數、降低信息儲量來降低分辨率，從而提高算法運行速度，適用于大空間環境的數據建模。本文針對重離子治癌治療床上病灶要在等中心的近端有較高的定位精度和遠端有快速移動的要求，提出在平面坐標系{O0:x0,y0}中利用扇形柵格法對病灶所處的運動空間進行分割，假定扇形柵格中的最小面積與病灶面積近似相等，扇形柵格中有障礙物空間的柵格定義為障礙柵格，記為黑格，在柵格數組中標為1；其余為自由柵格，記為白格，在柵格數組中標為0。扇形柵格法劃分的治療床工作空間的柵格模型如圖3所示，以數據形式存儲地圖信息的01矩陣如圖4所示。

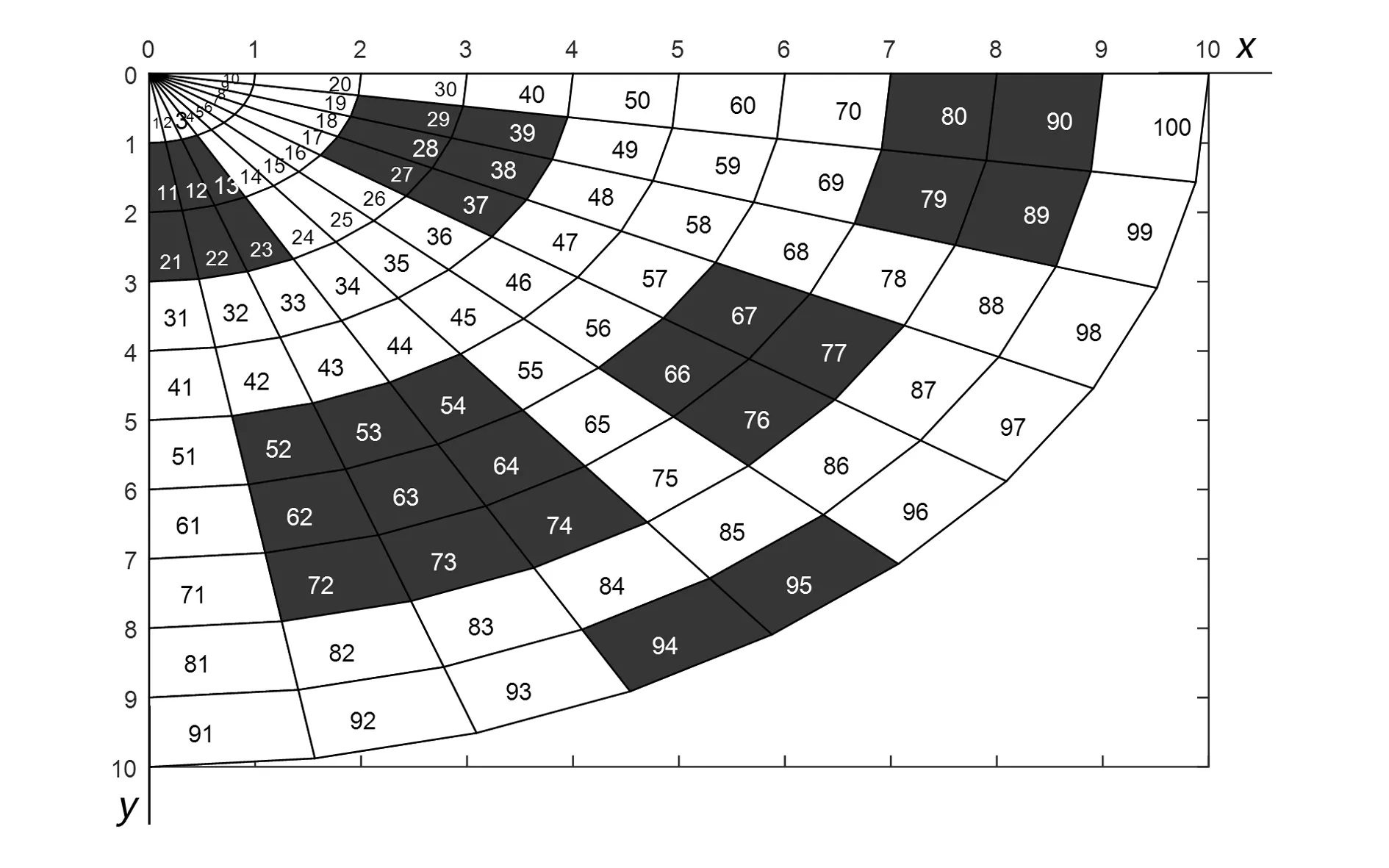
圖3 治療床工作空間劃分圖

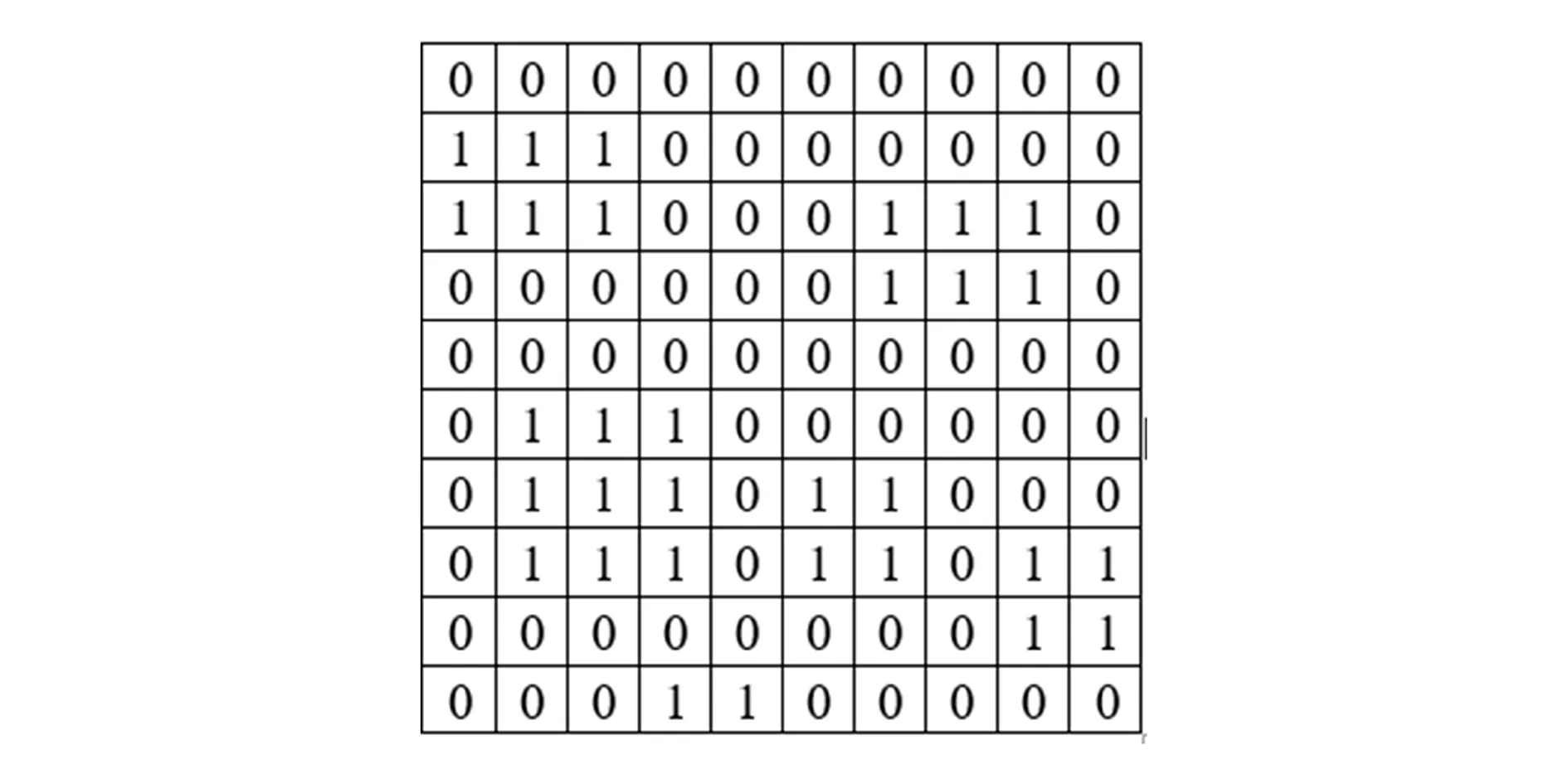
圖4 治療床空間的柵格數組表

圖3的表示方法為直角坐標法，病灶在坐標系{O0:x0,y0}中的坐標由式(1)可得：

(3)

記l為任意柵格，設TS為柵格集合；記NK={n1,n2,…，nm},為障礙格柵集合，MK為可行格柵集合，令K={1,2,…,n}，為格柵序號集合。設病灶初始點為lbegin,等中心點的序號1柵格設為目標終點lend；lbegin，lend都屬于可行格柵集合[6]。任意自由格柵間的距離D按照格柵中心點的距離計算：

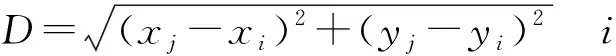
(4)

式中：S為位置矩陣，S=[s1,s2，…，si]

距離因子ηij計算公式為：

(5)

采用序號法和矩陣坐標點法相結合的方式來構建所有柵格的數據模型和編碼。

1)序號法: 如圖3所示，對每個柵格進行編號，標識的柵格記為ln，例如序號為1(目標終點)的柵格記為l1；病灶的位置序號si由式(6)決定。

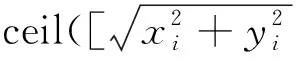
(6)

2)矩陣坐標點法:如圖3所示的坐標系中的每一柵格中心Z坐標值固定，可用直角坐標表示法(x,y)唯一標識,格柵的x坐標值存儲到SS矩陣中，y坐標值存儲到FF矩陣中。

n=a+Nxb

(7)

(8)

(9)

式中:n為某一柵格序號；Nx為圓弧劃分的柵格數；Ny為最大半徑值；mod表示取n/Nx的余數；int表示取n/Ny的整數。

上述模型就是重離子治癌治療床上的病灶環境模型，模型中等中心點附近分辨率高，有利于點B精確運動到等中心附近，柵格外部為大柵格，分辨率低，有利于路徑快速搜索。

2 算法建模及分析

蟻群算法最早是由學者Marco.Dorigo等提出的一種模擬螞蟻覓食行為的仿生算法，充分利用了蟻群能夠搜索到蟻巢到食物源之間最短路徑的集體尋優特征來構造最優解，具有良好的并行和反饋機制[7]。針對病灶移動路徑優化問題，利用該算法對病灶移動路徑進行尋優。

2.1 狀態轉移概率的選擇

(10)

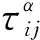
2.2 改進的信息素更新

當所有螞蟻都走完一次搜索路徑時，就要對成功尋到終點的螞蟻經過的路徑進行信息素全局更新。過去的信息素逐漸消失，增加新的信息素。為了提高算法的收斂速度，利用式(11)～ (14)來改進全局信息素的更新機制[9]。

(11)

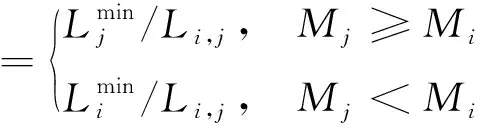
(12)

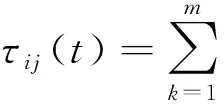
(13)

τij(t+n)=(1-ρ)×τij(t)+Δτij(t)

(14)

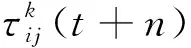
2.3 蟻群算法參數調整

算法中參數α,β和ρ對算法搜索能力以及收斂速度影響較大。針對算法初期信息素積累少、搜索速度慢，后期初始信息素作用小、信息素交換弱的問題[10]，需要修改α，β值，規則如下：

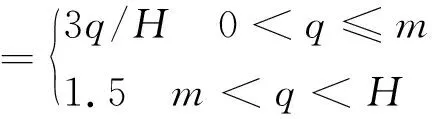
(15)

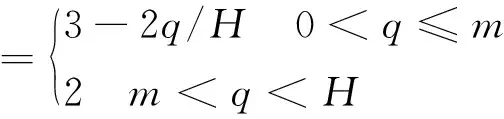
(16)

式中：m為臨界次數；q為當前循環次數;H為循環的最大次數。本算法中m=25，H=50。

改進的蟻群算法在20×20的方形柵格中進行路徑規劃，與改進前的蟻群算法相比，收斂次數和路徑長度均顯著減少，如圖5所示。

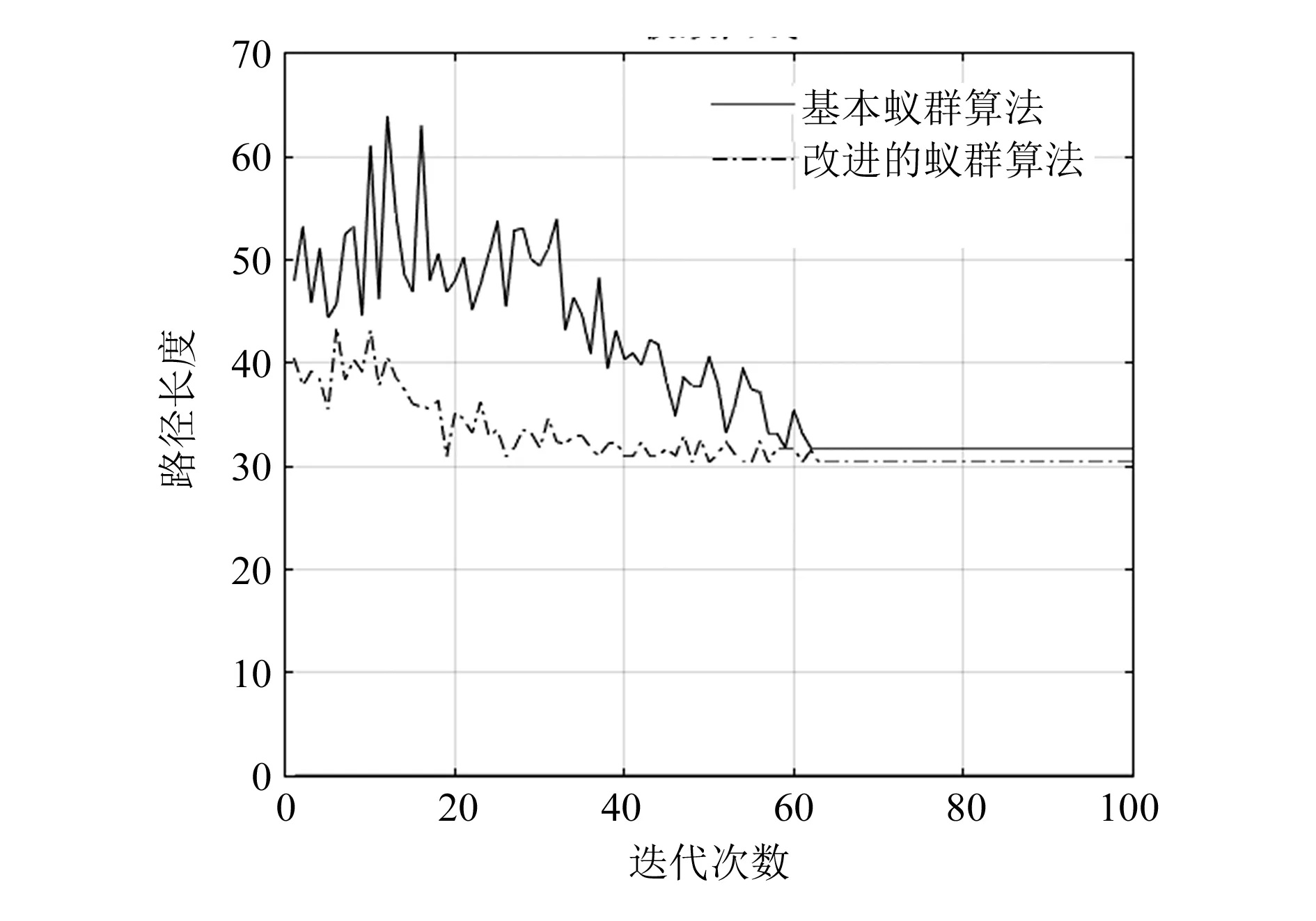
圖5 算法在20×20柵格環境中收斂曲線

2.4 蟻群算法實現流程

改進的蟻群算法在模型中的應用：將若干只螞蟻依次放在起始點lbegin，在柵格范圍內尋找目標終點lend，按輪盤賭法選擇路徑的下一個節點，記錄本輪到達目標終點所有螞蟻的路徑信息，更新全局信息素并保存,篩選出本輪路徑最短的那只螞蟻的路徑信息，即得到本輪的最優路徑；進行下一輪循環，直到達到所設定的循環次數，輸出最短路徑。算法流程如圖6所示。

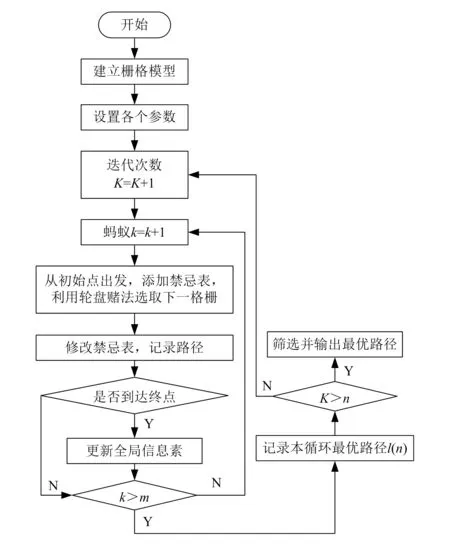
圖6 蟻群算法流程圖

3 仿真結果與分析

選取參數ρ為0.4、k為30、K為50進行仿真；改進后的算法在不同的柵格模型中得到的最優路徑的路線圖如圖7～圖10所示，收斂曲線圖如圖11所示。由圖可知，扇形柵格模型路徑的路徑長度和收斂次數都呈現減少趨勢，且等中心點附近的扇形柵格密度高，因此扇形柵格有利于病灶定位；由于柵格密度的增大，10×10的扇形柵格的收斂次數比20×20少，但柵格密度增大，自由柵格數目增多，使得20×20的路徑長度比10×10的短，綜合考慮的情況下，建議選取10×10的扇形柵格模型，收斂時間短，路徑長度適中，有利于病灶快速準確定位。由此可知,扇形柵格模型的蟻群算法在重離子治癌病灶定位的應用是有效可行的。

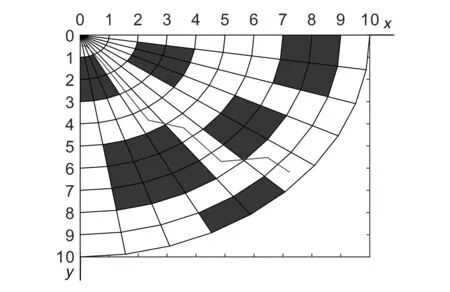
圖7 10×10扇形柵格路徑圖

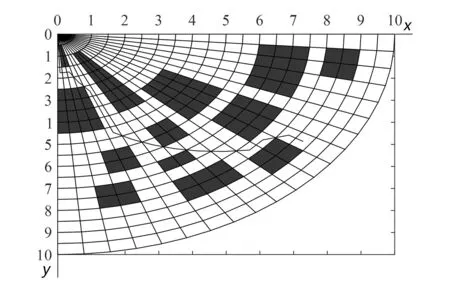
圖8 20×20扇形柵格路徑圖

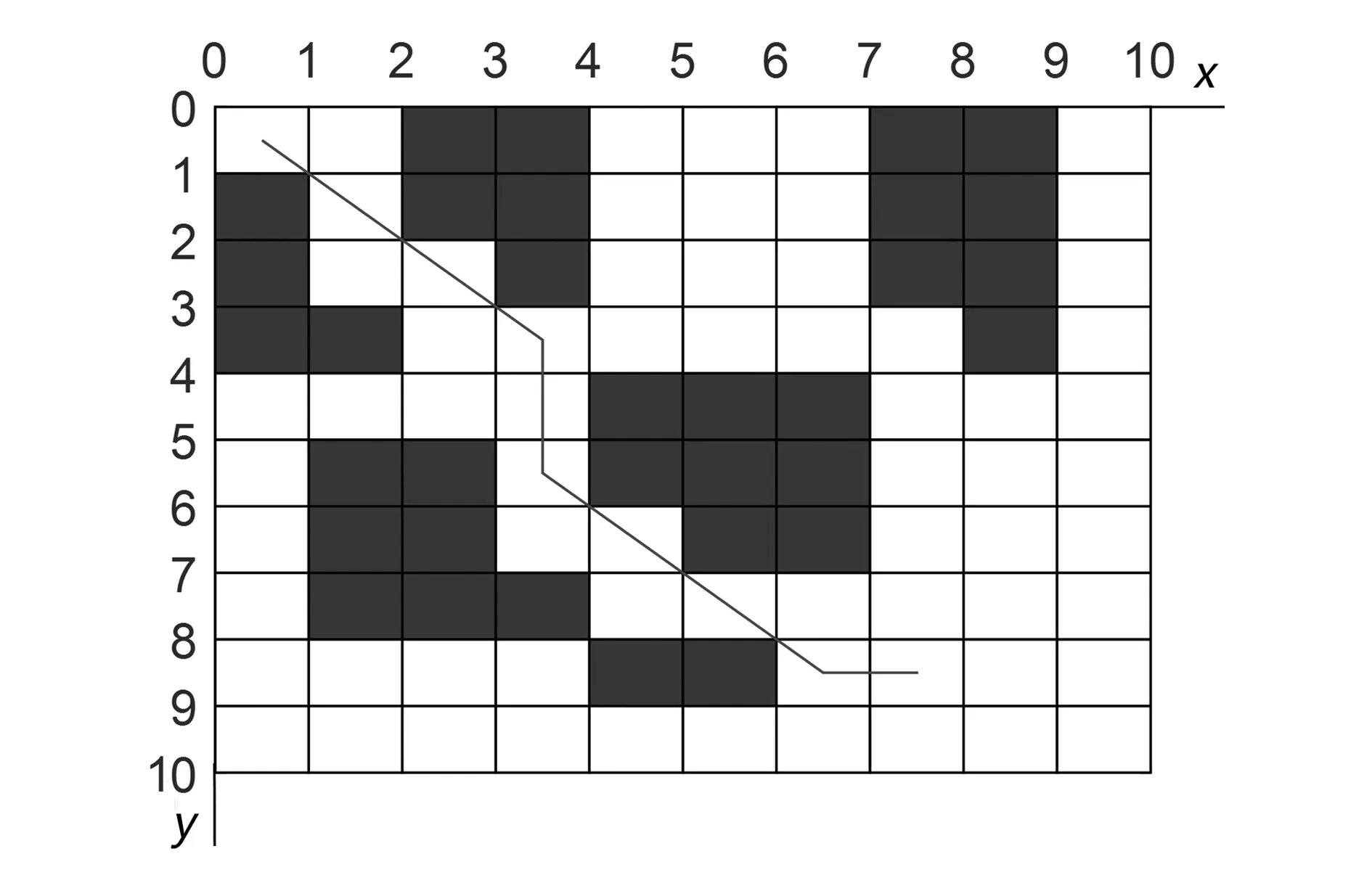
圖9 10×10方形柵格路徑圖

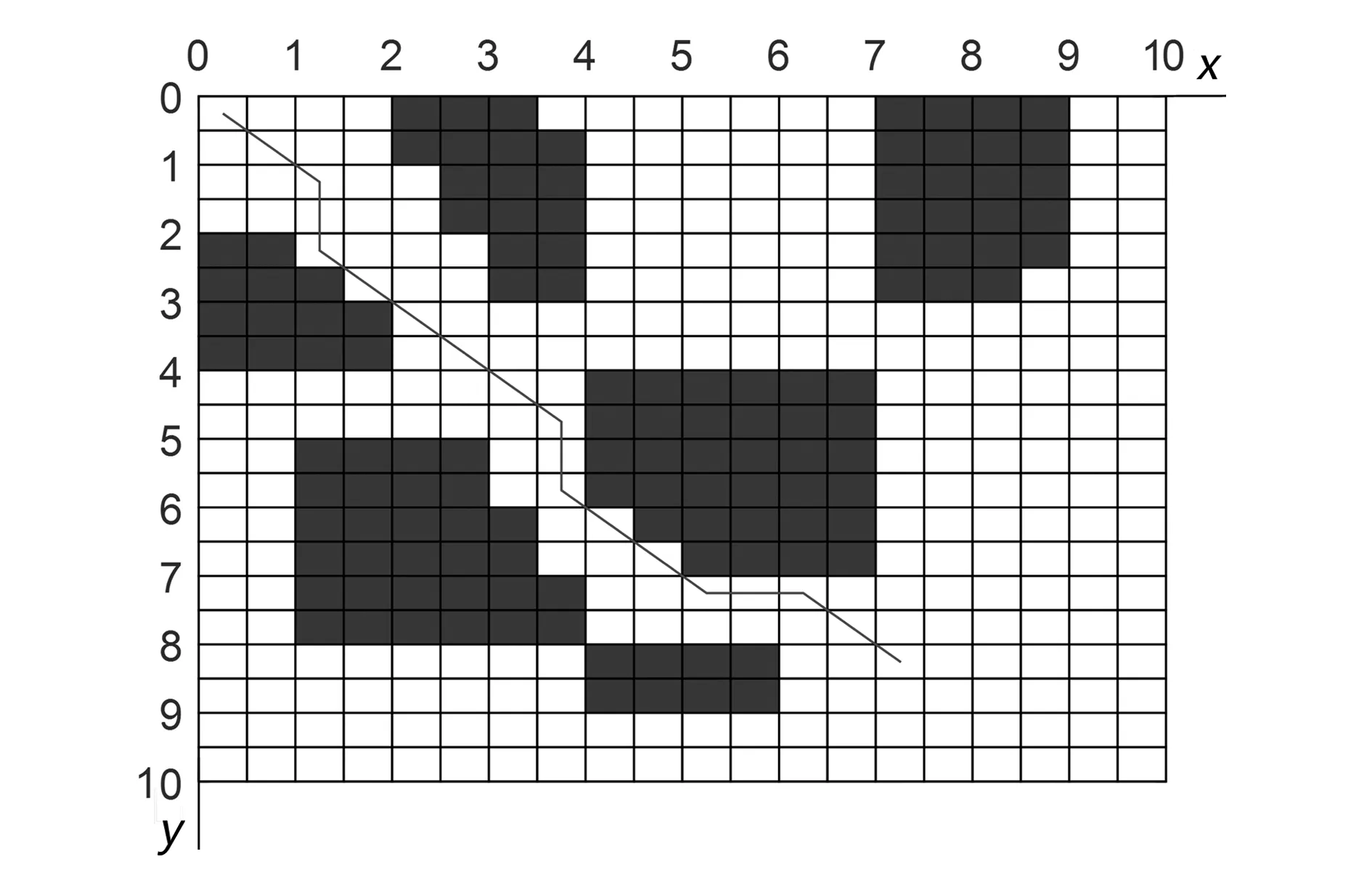
圖10 20×20方形柵格路徑圖

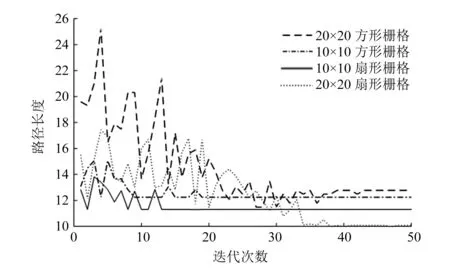
圖11 收斂曲線圖

4 結束語

在路徑規劃中，采用扇形柵格法對重離子癌癥治療床進行建模，可提高癌癥患者病灶在等中心的定位精度，扇形格柵有利于旋轉軸的運動，便于實現控制運動軸。本文用改進的蟻群算法對重離子治癌治療床上的患者病灶進行路徑規劃，得到優化的最佳軌跡，有效縮短了患者擺位時間，提高了重離子治癌系統的治療效率，保證了重離子治療癌癥的質量。MATLAB環境下對新的柵格蟻群算法進行仿真，結果表明：該算法增強了選擇路徑的隨機性，減少了收斂次數，為重離子治癌治療床運送病人提供了可靠依據，為后續的癌癥治療應用奠定了堅實的基礎。