雙級全預混燃氣灶引射器的理論分析

沈金晨，蘇 磊

(南京工業大學能源科學與工程學院，江蘇 南京 211816)

與傳統大氣式燃氣灶相比，全預混燃氣灶能實現燃氣和空氣的全預混燃燒，從而使火焰溫度和熱效率提高，同時減少CO和NOx的排放量，因此受到很多學者的重視[1-3]。全預混引射器可實現燃氣與其完全燃燒所需空氣的充分預混，是全預混燃氣灶的重要組成部件，因此研究和開發全預混引射器是全預混燃氣灶研究和應用中必須解決的關鍵問題。

目前，關于單級引射器性能的研究較多，許多學者對引射器的混合特性、引射器特性方程及引射器的可調性等進行了研究[4-7]。陳輝等[8]研究了工作流體壓力對引射器性能的影響，發現增加工作流體的壓力可以增大引射系數，但是當工作流體壓力超過臨界值后，繼續增加反而會引起引射系數的下降。宋力釗等[9]研究了幾何參數對引射器性能的影響，結果表明，在一定工況下存在一最佳的喉部和混合管直徑使引射系數最大。

雙級引射器通過階段性引射[10]有利于實現燃氣與空氣的全預混，目前對雙級引射器應用于燃氣灶上的研究還相對較少。童偉明等[11]通過實驗對比了單、雙級引射低壓加熱器性能的優劣，實驗結果表明，雙級引射器的引射系數比單級引射器的引射系數提高了120%，雙級引射器在綜合性能上比單級引射器要好。

本文提出了一種新的雙級全預混燃氣灶引射器的結構。以3.5 kW燃燒功率的民用天然氣燃氣灶為例，在天然氣壓力和天然氣額定流量確定的情況下，進行了雙級引射器的結構設計和理論建模，分析雙級引射比、截面比和引射壓差對引射器性能的影響。

1 理論模型

雙級引射器本質上是單級引射器的重復，為方便敘述，現以單級引射器的理論模型為例，介紹雙級引射器建模方法。單級引射器主要由噴嘴、吸入室、混合管和擴壓管組成，圖1為單級引射器結構示意圖。

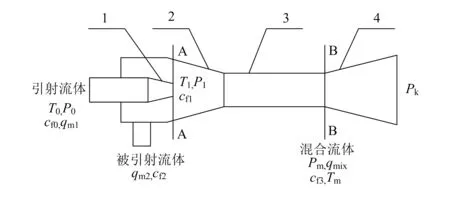
1—噴嘴；2—吸入室；3—混合管；4—擴壓管

1.1 噴嘴

設噴嘴內部流動為可逆絕熱過程，理論描述如下：

(1)

(2)

噴嘴出口引射流體的實際流速cf1為：

(3)

式中：T0,T1分別為噴嘴進口、出口引射流體溫度，K；P0,P1分別為噴嘴進口、出口引射流體壓力，Pa；k為引射流體絕熱指數；cp為引射流體定壓比熱容，kJ/(kg·K)；cf0為噴嘴進口引射流體流速，m/s；φ為不可逆流動的速度修正系數，一般取0.92～0.98。

1.2 吸收室和混合管

引射器混合段的內部氣體混合過程十分復雜，需通過動量守恒、連續性方程和能量守恒定律來進行理論分析，根據過程特點把吸收室和混合管看作一個整體，統稱為混合管。

首先在圖1 所示的A-A和B-B截面上建立混合管動量方程：

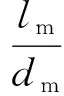
(4)

式中：qm1,qm2,qmix分別為引射流體、被引射流體和混合氣體的質量流量，kg/s；cf2,cf3分別為被引射流體進口流速和混合管出口混合氣流速，m/s；ψ為混合管速度場不均勻系數；Am為引射器混合管的橫截面積，m2；Pm為混合管出口壓力，Pa；λ為摩擦系數(與混合管內的雷諾數Re有關)；lm為混合管長度，m；dm為混合管直徑，m；ρmix為混合管內混合氣的密度，kg/m3。

速度場不均勻系數ψ取決于速度場的分布狀況[16]。拋物線速度場，ψ=1.33；穩定的紊流速度場(Re=10 000)，ψ=1.02；矩形速度場，ψ=1.00。本文中的速度場為穩定的紊流速度場，故ψ=1.02。

混合管能量守恒方程：

(5)

式中：h1,h2,hmix分別為引射流體、被引射流體和混合氣的當地焓值。

混合管質量守恒方程：

qmix=qm1+qm2

(6)

混合管出口氣體狀態方程：

PmqV,mix=qmixRgTm

(7)

式中：qV,mix為混合管中混合氣的體積流量，m3/s；Rg為混合管中混合氣的氣體常數，kJ/(kg·K)；Tm為混合管出口混合氣溫度，K。

1.3 擴壓管

考慮擴壓管的擴張程度及流動阻力損失，則混合氣在擴壓管出口截面的壓力Pk為：

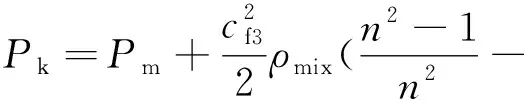
(8)

式中：n為擴壓管的擴張程度，即擴壓管出口截面積與混合管截面積的比值，與引射器的形狀有關[12]，n的值一般取2～3；ξd為擴壓管阻力損失系數，與n有關。

2 雙級全預混燃氣灶引射器

圖2為本文提出的雙級全預混燃氣灶引射器的結構示意圖，該引射器為雙級串聯形式，第一級引射器混合管的出口即為第二級引射器噴嘴的進口。第一級引射器的引射流體為風機提供的少量的空氣(即一級空氣)，被引射流體為天然氣，由一級空氣引射全部的天然氣；第二級引射器中，將第一級引射器混合后的氣體作為引射流體，引射全預混燃燒所需的剩余全部空氣(即二級空氣)，然后混合氣在第二級引射器混合管中充分混合后由擴壓管升壓后排出。

1—第一級噴嘴；2—第一級吸收室；3—第一級混合管；4—第二級噴嘴；5—第二級吸收室；6—第二級混合管；7—擴壓管

其工作原理如下：鼓風空氣(一級空氣)通過高于燃氣壓力的壓頭進入一級空氣噴嘴，在噴嘴中降壓增速后流出，引射從燃氣吸入室進入的天然氣，此時鼓風空氣壓力降到天然氣壓力[13](2 000Pa)；鼓風空氣引射天然氣后會在一級混合管內進行混合，并以一級混合氣的形式進入第二級引射器噴嘴，再經過降壓增速，當混合氣壓力降至大氣壓[13]時其流速升高，較高流速的混合氣從二級空氣吸入室引射全預混燃燒所需的全部剩余空氣(二級空氣)，之后在第二級混合管中充分預混，最后經擴壓管升壓排出。這個過程中，鼓風空氣、被引射的燃氣和被引射的二級空氣不停地發生動能的交換。

本引射器的優點是既利用了天燃氣原有壓頭引射空氣系數為0.6左右的空氣，又利用極少量的低壓一級空氣(空氣系數為0.1左右)引射空氣系數為0.4左右的空氣，滿足了全預混所需的空氣系數為1.1的空氣量。同時該引射器通過雙級引射，還具備一定的負荷調節能力。

2.1 引射器性能參數及評價指標

引射器性能參數主要有引射比μ、截面比k和引射壓差ΔP等。

引射比μ：指被引射流體的質量流量與引射流體質量流量的比值，它反映了引射器的引射能力。一級空氣與燃氣質量流量的比值為一級引射比，一級混合氣與二級空氣質量流量的比值為二級引射比。當天然氣流量和空氣流量一定時，隨一級空氣流量的增加，一級引射比μ1減小，對應的二級引射比μ2也減小。

截面比k：指各級引射器中的混合管截面積與噴嘴出口截面積之比，其值的大小影響混合氣在混合管出口處的流速和壓力，以及混合氣在混合管內的流動阻力。一級截面比k1為一級混合管與一級空氣噴嘴的截面比，二級截面比k2為二級混合管與二級噴嘴截面比。

引射壓差ΔP：指引射流體工作壓力與被引射流體工作壓力的差值，其值反映了引射流體所具有的能量，直接反映其引射低壓流體的能力。雙級引射器有兩級引射壓差ΔP1和ΔP3，一級引射壓差為一級鼓風空氣與天燃氣的壓力差，二級引射壓差為第一級引射器出口的混合氣與二級空氣的壓力差。由于兩級引射器串聯布置，因此第二級引射壓差的變化實質上是由一級引射壓差引起的，在數值上隨一級引射壓差動態變化。

被引射流體壓差ΔP作為引射器性能評價指標，是指被引射流體經過引射器混合管和擴壓管后壓力升高的值，它反映了被引射流體經高壓流體引射后所具有的能量。文中一級混合管出口壓力與天然氣的壓力差為一級被引射流體壓差ΔP2，擴壓管出口和二級引射空氣的壓力差為二級被引射流體壓差ΔP4。

2.2 引射器設計參數

本文所涉及的引射器參數見表1和表2。

表1 燃料性能參數

表2 初始設計參數

本文的可變參數見表3～表5。

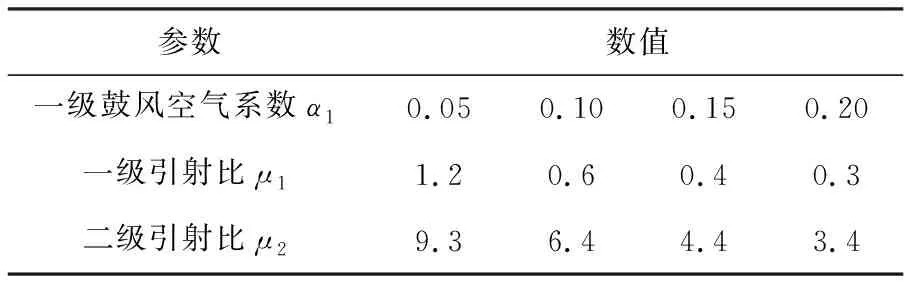
表3 不同的一級鼓風空氣系數和引射比

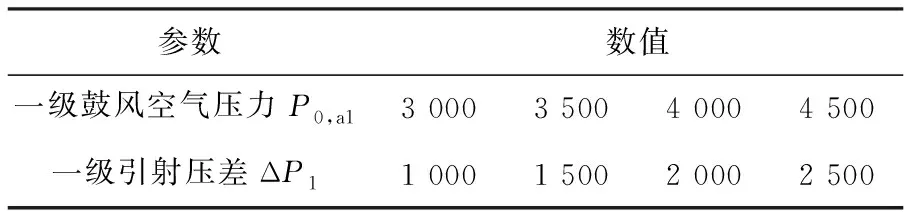
表4 不同的一級鼓風空氣壓力和引射壓差 Pa

表5 不同的截面比

3 結果及分析

以3.5kW天然氣民用灶為例，分析額定功率下，即天然氣壓力和流量確定時，一級鼓風空氣系數α1、壓力P0，a1以及截面比k1和k2對引射器雙級引射性能的影響。

3.1 一級引射性能分析

圖3對比了一級引射中，當一級鼓風空氣系數α1為0.05、對應的一級引射比μ1=1.2時，一級被引射流體壓差ΔP2隨一級引射壓差ΔP1和一級截面比k1的變化情況。

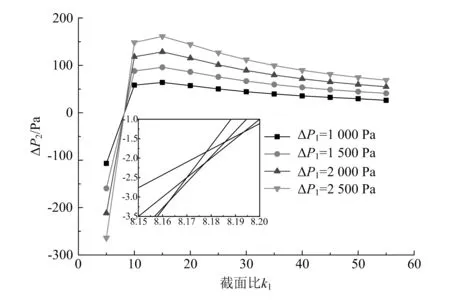
圖3 μ1=1.2時ΔP2隨ΔP1和k1的變化

結果顯示，當一級鼓風空氣系數α1為0.05即一級引射比μ1=1.2時，隨著一級截面比k1的增大，一級混合管出口被引射流體壓差ΔP2先增大后減小，當截面比k1=15時，不同的一級引射壓差ΔP1都得到了最大的被引射流體壓差ΔP2。這說明，在相同引射比時，雖然引射壓差不同，但都存在一個共同的最佳截面比，使被引射流體獲得最大壓升。原因是當截面比過小時混合管直徑較小，混合管出口流速和混合管內的流動阻力與截面比較大時相比顯著增大，導致混合管出口壓力明顯減小；而截面比過大時，混合管直徑較大，雖然混合管沿程阻力和出口流速下降，會使混合管出口壓力上升，但其升幅小于混合管截面積增大使出口壓力降低的幅度，因此仍會導致混合管出口壓力逐漸減小。

從圖3還發現，當截面比小于8.15時，大引射壓差ΔP1可獲得小被引射流體壓差ΔP2，且ΔP2為負值，說明在設計引射器時，截面比不宜過小。原因是當引射流體流量一定時，由于噴嘴直徑減小，過高的工作壓力使得噴嘴出口流速增大，同時小截面比使混合管直徑縮小，這些都大大增加了流動過程中的不可逆能量損耗，導致引射性能惡化。當截面比大于8.20時，被引射流體壓差ΔP2隨引射壓差ΔP1的增加而增加，且ΔP2大于零，滿足引射器升壓的基本條件。總之，當一級引射比μ1一定時，存在一個最小截面比和一個最佳截面比，且其值基本不受一級鼓風壓力的影響。

圖4對比了在一級鼓風壓力為3 000Pa即一級引射壓差ΔP1=1 000Pa、一級鼓風空氣系數α1從0.05增加到0.20使一級引射比μ1從1.2降低到0.3時，一級混合管出口被引射流體壓差ΔP2隨一級引射比μ1和一級截面比k1的變化情況。

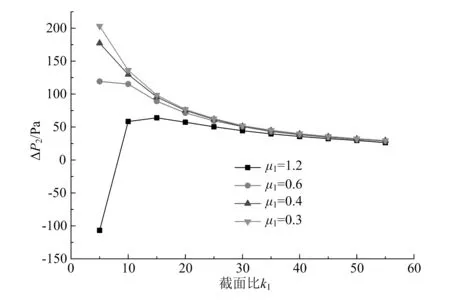
圖4 ΔP1=1 000Pa時ΔP2隨μ1和k1的變化

結果顯示，當被引射的天然氣流量一定時，隨著一級鼓風空氣系數α1的增加，一級引射比μ1減小，一級最佳截面比k1也減小。這是因為：隨一級空氣流量的增加，在進出口壓力不變的情況下，要求噴嘴出口直徑變大，而被引射流體質量一定，使一級混合管直徑相對于噴嘴直徑減小，即一級最佳截面比減小。

當截面比小于15時，一級引射比越小，即一級空氣流量越大，相同截面比下的被引射流體壓差越大。隨著截面比的增加，引射比對被引射流體壓差的影響變小，當截面比大于35時，各引射比下的被引射流體壓差趨于相等且隨截面比的增加緩慢下降，此時引射比對被引射流體壓差的影響可以忽略，即一級空氣流量繼續增大不會增加被引射流體壓差。但截面比增加，會小幅降低被引射流體壓差，使一級引射器的引射性能下降，原因是當截面比足夠大時，工作流體流量變化使混合管內的流動阻力和出口流速發生變化，但其對出口壓力的影響遠不及截面增加對出口壓力的影響大。

總之，在額定天然氣流量下，一級最佳截面比k1隨一級引射比μ1的增大而增加；隨著截面比繼續增加，一級被引射流體壓差受引射比和截面比的影響大大減弱。

圖5顯示了一級引射中，當一級截面比k1=15時，隨一級鼓風壓力和一級鼓風空氣系數α1的增加，一級引射壓差ΔP1和一級引射比μ1對一級被引射流體壓差ΔP2的影響規律。

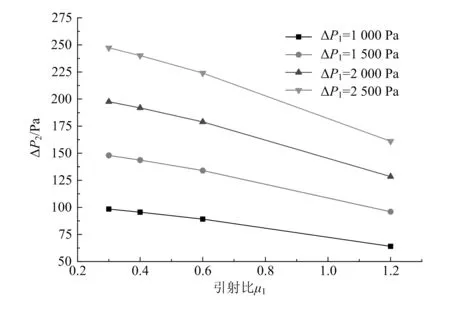
圖5 k1=15時ΔP2隨ΔP1和μ1的變化

結果顯示，鼓風壓力一定時，隨著引射比的增大，被引射流體壓差減小，即一級被引射流體壓差隨一級空氣流量的減小而降低。當一級鼓風空氣系數α1一定時，引射比不變，一級被引射流體壓差隨一級鼓風壓力的升高而增大。

綜上所述，一級鼓風空氣系數α1為0.05時，一級引射比最大，最佳截面比k1為15，此時的被引射流體壓差隨鼓風壓力升高而增大；在最小鼓風壓力為3 000Pa時，一級被引射流體壓差達到50Pa以上，足以滿足二級引射的要求，若再增加鼓風壓力，會使被引射流體壓差過高，需增大截面比，從而需加大引射器的結構尺寸。因此采用0.05的一級鼓風空氣系數α1和1 000Pa的一級引射壓差，將使一級引射器具備較好的引射性能和較優的結構。

3.2 二級引射性能分析

以一級引射器的最優結構和工況作為基準，分析二級引射器及鼓風壓力對二級引射性能的影響。當全預混燃燒所需空氣系數為1.1時，則二級空氣吸入系數為1.05，額定功率下的二級引射比μ2=9.3。

圖6對比了當一級引射的α1=0.05、μ1=1.2、k1=15、二級引射比μ2=9.3時，二級被引射流體壓差ΔP4隨一級鼓風壓力(一級引射壓差ΔP1)和二級截面比μ2的變化規律。

圖6顯示，隨著二級截面比k2的增大，被引射流體壓差ΔP4先增大后減小，當截面比k2=130時，不同的一級引射壓差ΔP1都得到了最大的被引射流體壓差ΔP4。這說明，當二級引射比確定時，會

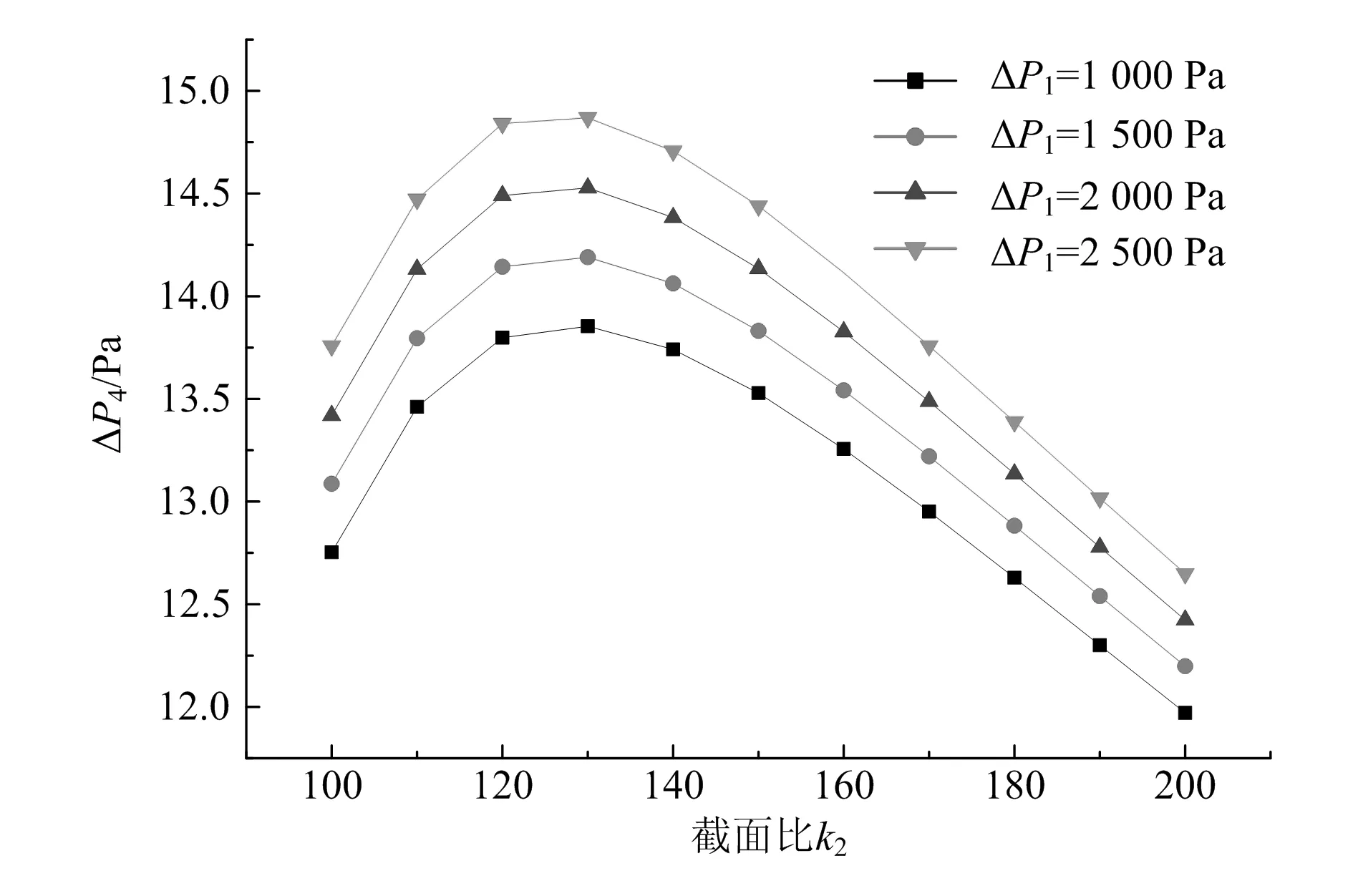
圖6 μ2=9.3時ΔP4隨ΔP1和k2的變化

存在一個最佳的二級截面比，使被引射流體獲得最大壓升，增加或減小截面比都會降低二級引射器的增壓性能，而增大引射壓差，會提高引射器的增壓性能。這是因為，當一級引射結構確定時，隨一級鼓風壓力的增加，一級引射壓差ΔP1增大，一級混合管出口壓升ΔP2也增大，意味著二級引射流體的工作壓力隨之增加，從而提高了二級被引射流體的壓升ΔP4。

圖7對比了一級鼓風壓力為3 000Pa即一級引射壓差ΔP1=1 000Pa、一級最佳截面比k1=15時，二級擴壓管出口被引射流體壓差ΔP4隨二級引射比μ2和二級截面比k2變化的情況。當一級鼓風空氣系數α1從0.05升到0.02時，二級空氣系數從1.05降到0.90，二級引射比μ2從9.3降到3.4。

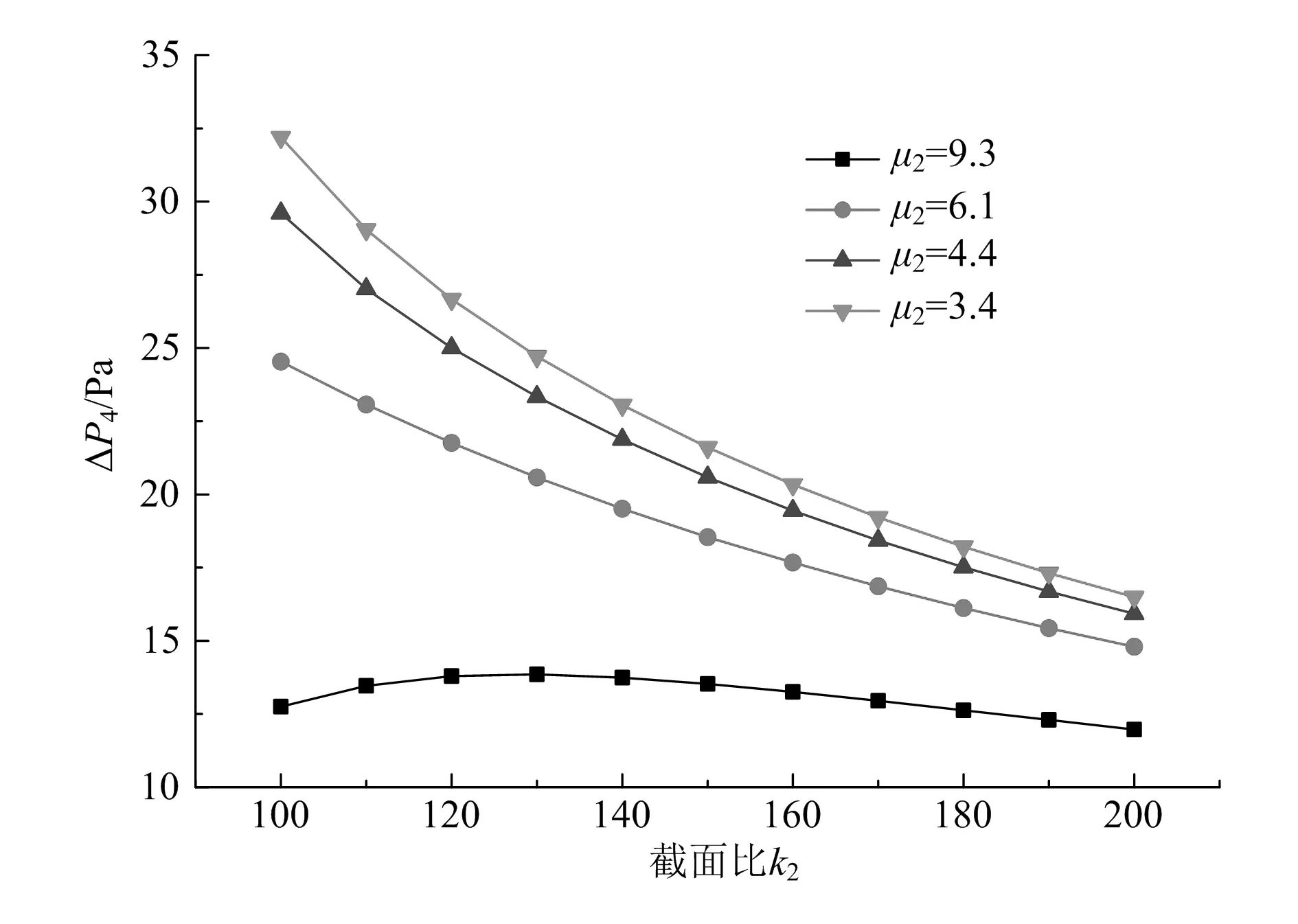
圖7 ΔP1=1 000Pa、k1=15時ΔP4隨μ2和k2的變化

結果顯示，當μ2=9.3時，存在一個最佳二級截面比k2=130；當二級截面比相同時，隨二級引射比的減小，即一級鼓風空氣系數α1的增加，二級被引射流體壓差增大，但都隨截面比的增大而減小。

另外，二級被引射流體壓差ΔP4反映了雙級引射器擴壓管出口表壓，而此壓力是用于克服燃氣灶系統流動阻力的，一般取值在幾Pa到十幾Pa之間。圖7顯示，當ΔP1=1 000Pa、α1=0.05、μ2=9.3、k1=15，k2在130左右時，引射器出口壓力足以滿足系統阻力的需求，若再增大鼓風壓力和鼓風流量，一方面增大了鼓風機的功率，同時增加了引射器出口壓力，導致能量上的浪費，若用增加截面比來降低出口壓力，則增大了引射器結構尺寸，成本提升，也是浪費。

4 結論

在氣源參數確定的情況下，本文在額定工況下對雙級全預混燃氣灶引射器進行了理論建模與結構設計，得到如下結論：

1)在一定的引射比下，雙級燃氣全預混引射器的兩級都存在一個不隨引射壓差變化的最佳截面比，使被引射流體壓差最大，且最佳截面比的值隨引射比的增加而增大。

2)在一定的引射比下，引射器存在一最小截面比，且此最小截面比基本不受引射壓差的影響。當截面比小于最小截面比時，被引射流體壓差為負值，不具備引射壓縮流體的能力；當截面比大于最小截面比時，被引射流體壓差隨引射壓差的增加而增大。

3)在一定的引射壓差下，最佳截面比隨引射比的增加而增大，被引射流體壓差隨引射比的增加而減小。

4)在一個相對較小的截面比下，引射比越小，被引射流體壓差越大，但隨著截面比的持續增大，被引射流體壓差受引射比的影響逐漸減小，并隨截面比的增加呈緩慢小幅下降的趨勢。