基于偏最小二乘方法的ARIMA模型在股票指數預測中的應用

方坷昊,趙 凌

(1.四川文理學院教務處，四川達州635000；2.四川師范大學數學與軟件科學學院，四川成都610068)

1 引言

股票市場作為國家經濟的重要組成部分，對國家經濟有較強的影響，其活躍程度更是衡量國家經濟的一項重要指標.此外，股票指數的上漲(下跌)幅度大小亦對投資者的投資決策有著積極(消極)的作用，間接地反饋了股市的活躍程度信息.而股票指數作為股票市場的重要綜合指標，所以較普通股票而言，對股市有著更為重大的影響，更具備研究意義.

1999年，國內學者最早在國內給出了ARIMA模型在股票價格預測方面的應用;[1]2006年，覃思乾利用ARIMA模型與GM模型的組合模型對股票指數進行預測；[2]2011年，李美利用ARIMA模型對股價進行預測，并利用傅立葉修正方法進行修正；[3]2012年，王丹楓實證分析了從投資者視角來進行股票價格預測的可能性.ARIMA模型結合股票指數序列的自身規律對股票指數進行了較好的預測，但并未考慮其他的相關變量對股票指數的影響.[4]1983年，偏最小二乘回歸由S.Wold和C.Alban首次提出后，該方法在關于存在多重共線性問題的解決方面迅速得到應用，在股市方面的研究亦有廣泛應用，2004年，鄭承利應用偏最小二乘法對美式期權的仿真定價問題進行了研究；[5]2010年，姬強應用偏最小二乘法對中美股票市場的協動性作出分析.[6]偏最小二乘回歸在股票指數預測的應用上考慮了把股票指數影響較大的變量納入自變量組進行回歸分析，較好地對各個相關指標的多重共線性進行消除，但并未利用自身存在的規律性進行分析.

本文的意義在于以上證指數為例利用偏最小二乘方法對股票指數進行回歸分析，將ARIMA模型得出的股票指數預測值歸為原始變量組，在建立偏最小二乘回歸模型時充分地利用了股票指數自身存在的規律性，且納入投資者視角所關注的股票指數相關變量，建立了在真正意義上充分考慮了投資者行為的偏最小二乘回歸模型，在統計于行為金融方面的探究中有重大意義.

2 數據與模型

2.1 數據來源

本文數據包括上海證券交易所公布的2016年1月到2016年6月上證指數數據、上證指數證券成交量、人民幣對美元匯率、上證指數期貨價格；美國NASDAQ證券交易所公布的NASDAQ指數數據，變量選取如下：因變量Y為上證指數當日價格、自變量X1為上證指數當日ARIMA模型預測價格、X2為上證指數上一日交易量，其數值大小代表每日交易所成交數量，一定程度上能反映短期內股民投資意愿、X3為上證指數上一日期貨價格，此變量的意義在于反映市場對目標股票的漲跌期望，同時對目標股票價格具有一定的指導意義、X4為美元對人民幣匯率，反映短期內金融市場的活躍程度、X5為美國NASDAQ指數價格，作為NASDAQ世界最大的股票交易市場，其指數價格作為同類型股票對上證指數價格亦具有相當的指導意義，如表1所示：

表1 變量關系表

2.2 模型理論

2.2.1 ARIMA模型

自回歸滑動平均模型(Auto-RegressionIntegrated Moving Average Model，ARIMA)是由自回歸模型(Auto-Regression Model，AR)、差分項I(d)和滑動平均模型(Moving Average Model，MA)兩部分組成，主要用于短期時間序列建模，與傳統相比，優勢在于建模簡便，對非線性模型有較好的解釋能力.且定義如下：

若{εt}是高斯白噪聲WN(0,σ2)，φ1,φ2,…,φp(φp≠0),?1,?2,…,?q(?q≠0)，皆為實數，則稱

φ(B)dXt=θ(B)εt

為求和自回歸滑動平均模型，并記為ARIMA(p,d,q)模型.其中B為延遲算子，d=(1-B)d為差分算子，φ(B)=1-φ1B-φ2B2-…-φpBp為自回歸系數多項式，θ(B)=1-?1B-?2B2-…-?pBq為滑動平均系數多項式.

1.2.2 偏最小二乘回歸模型

偏最小二乘回歸(Partial Least Squares Regression，PLSR)是在1983年由S.Wold和C.Alban首次提出的， 是近年來應實際需要而生產和發展的一個有廣泛適用性的多元統計方法.在常見的多因變量對多自變量的回歸建模中，特別是在觀測值數量少以及存在多重相關性等問題時，該方法具有傳統的回歸方法所不具備的意義明確、計算簡便、省時、建模效果好、解釋性強等優點.

偏最小二乘回歸是一類解決由p個自變量X=(X1,X2,…,Xp)和q個因變量Y=(Y1,Y2,…,Yq)的n個觀測值組成的數據表存在多重相關性時的回歸分析問題的模型，首先偏最小二乘回歸不直接對X與Y進行回歸，而是先從X和Y中提取成分t1和u1，在提取成分時，有下列兩個要求：

a.t1和u1應盡可能大地攜帶他們各自數據表X和Y中的變異信息；

b.t1與u1的相關程度最大.

在第一輪提取后，分別實施X對t1的回歸及Y對t1的回歸，如果回歸方程已經達到滿意的精度，則算法終止；否則，將利用X被解釋后殘余信息以及Y被t1解釋后的殘余信息進行第二輪的成分提取，直到達到回歸方程滿意精度，算法終止.

若最終提取成分數量為m，則偏最小二乘回歸將通過施行yk對t1,…,tm的回歸，然后表達為yk關于原自變量x1,…,xp的回歸方程，k=1,2,…,q.

3 實證結果與分析

3.1 實證步驟

本文首先對上證股票指數序列進行ARIMA模型建立與分析：對股票指數序列做二階差分處理后序列平穩，采用ARIMA模型對其價格進行一個初步的預測后，模型擬合效果較為理想，為進一步提高預測精度，根據偏最小二乘回歸在處理多重共線性方面問題的優勢；第二步把ARIMA模型的預測結果納入原始變量組，記為X1、再選取上證指數上一日交易量X2、上證指數上一日期貨價格X3、上一日美元對人民幣匯率X4、美國NASDAQ指數價格X5四個對股票指數價格Y影響較大的變量作為原始變量組對股票指數作回歸分析，利用回歸分析進行擬合預測，研究表明，組合模型較ARIMA模型取得較大的修正效果.

3.2 ARIMA模型預測效果檢驗

3.2.1 平穩性檢驗

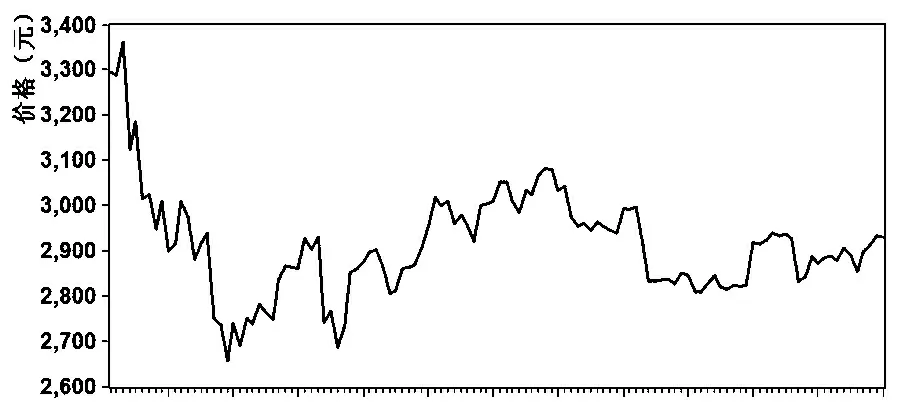
圖1 上證指數價格時間序列

首先在EVIEWS軟件中作出上證指數股票價格的時間序列圖(圖1)，由時序圖法，可見圖像變化并不規則，不存在對于一個確定的價格附近震蕩的現象，并無規律可言，認為該序列并不具有平穩性，需要對其做出差分處理；在對上證指數股票價格序列二階差分(DDLAVE)后，差分序列在0附近震蕩，初步確定平穩，對其做單位根檢驗(圖2)，可見該序列的ADF統計量的p值趨近于0，遠小于0.01，通過平穩性檢驗，上證指數股票價格二階差分序列為平穩序列，下面對該序列進行模型建立.

圖2 單位根檢驗圖

3.2.2 模型選擇

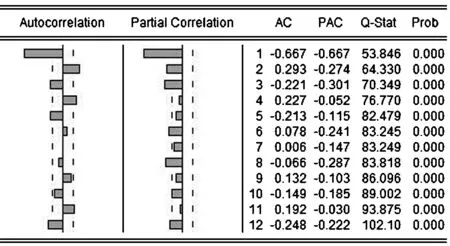
圖3 自相關檢驗圖

由自相關檢驗圖(圖3)，Q統計量對應p值均趨于零，可見模型并非白噪聲.我們對所要建立的ARIMA模型階數進行確定：首先，對上證股票指數二階差分序列做自相關檢驗后，得出該差分序列的自相關圖(圖3)，可見該序列的自相關系數與偏相關系數都具有拖尾性，考慮建立ARIMA模型，有圖三可見，自相關系數三階后有迅速下降且趨于0的趨勢，偏相關系數在二階后有迅速下降且趨于0的趨勢，因此建立ARIMA(1，2，1)、ARIMA(1，2，2)、ARIMA(2，2，2)、ARIMA(2，2，3)模型進行比較,模型對應結果如表2所示：

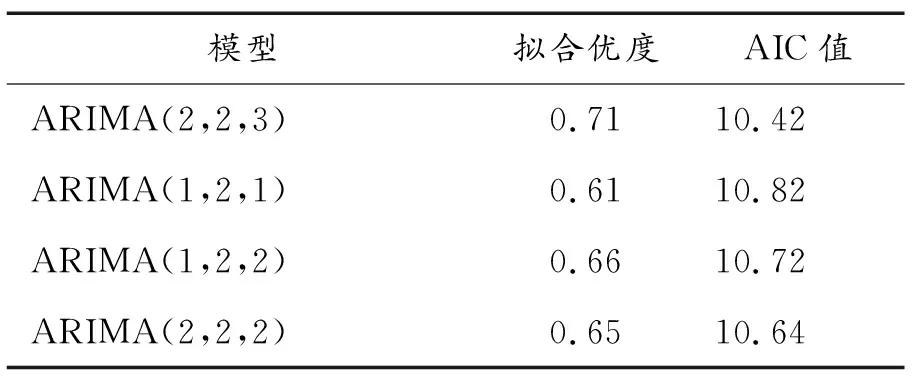
表2 ARIMA模型階數選擇

由表2可見ARIMA(2，2，3)模型在四個模型中擬合優度最大，AIC值最小，模型效果最好，所以對序列建立ARIMA(2，2，3)模型.

3.2.3 模型評價

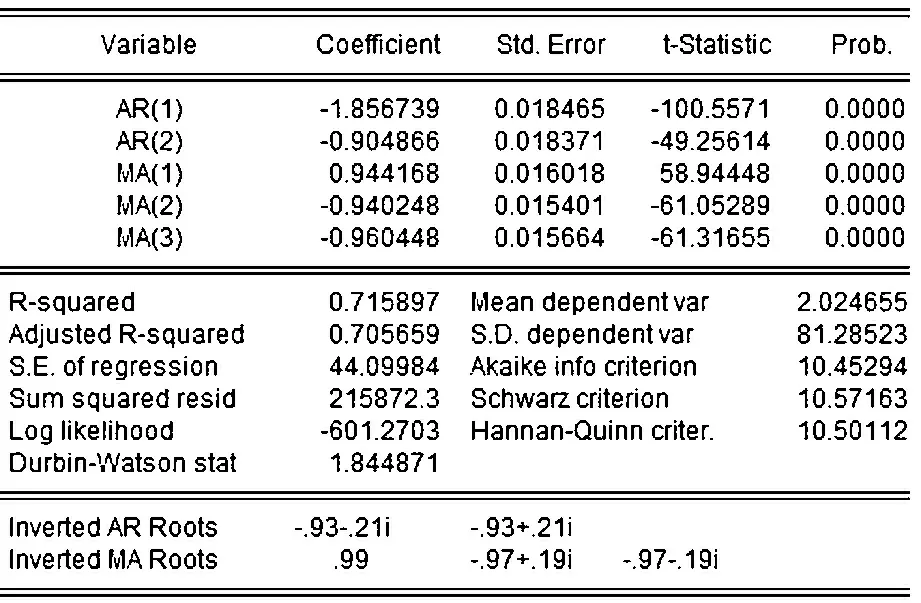
圖4 ARIMA模型

Xt=-0.905Xt-4-0.047Xt-3+1.809Xt-1-0.143Xt-1+εt+0.942εt-1-0.943εt-2-0.965εt-3

由圖四可見，對該模型做t檢驗后，各參數對應t統計量均處在較好水平，模型系數對應p值均小于0.01，通過顯著性檢驗；對殘差做白噪聲檢驗后，Q統計量對應p值均大于0.05，結果表明殘差為白噪聲，ARIMA模型為有效模型.結合上證指數與其ARIMA模型預測價格的時間序列圖(圖5)以及ARIMA模型對上證指數Xt的四期預測結果(表3)可見：模型的平均相對誤差率為0.5%，說明ARIMA模型能較好地預測出上證指數股票價格.

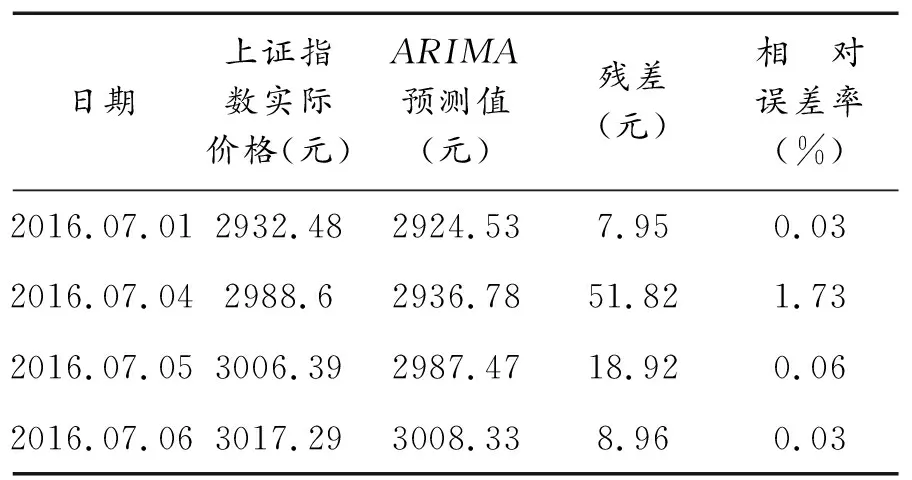
表3 ARIMA模型預測結果

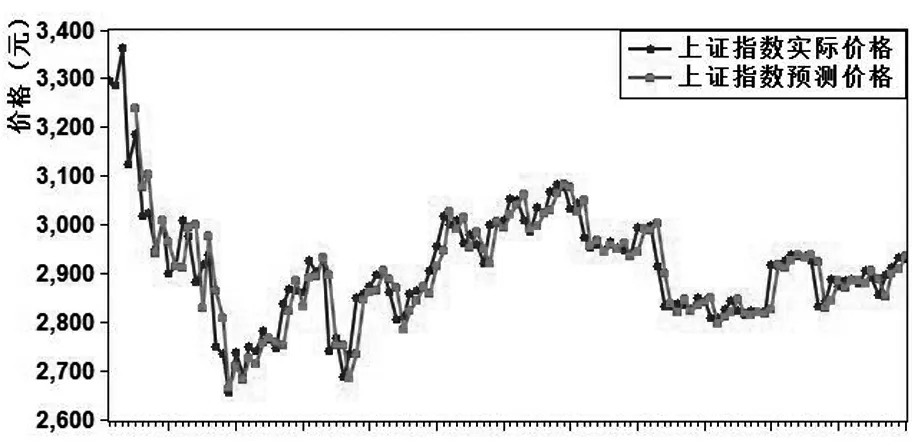
圖5 ARIMA模型擬合效果圖

3.3 偏最小二乘模型

3.3.1 模型建立

在2.2中，通過ARIMA模型對上證指數進行擬合預測，擬合優度達到0.71，平均相對誤差率為0.5%.為進一步提高預測精度，使用線性回歸對ARIMA模型進行修正,基于偏最小二乘方法處理復共線性數據上的適用性：首先把ARIMA模型預測值納入原始變量組，記為X1、再加入與上證指數價格相關的上證指數上一日交易量X2、上證指數上一日期貨價格X3、上一日美元對人民幣匯率X4、美國NASDAQ指數價格X5作為原始變量組進行偏最小二乘回歸分析，組合模型得出結果后與ARIMA模型輸出結果X1進行比較.

本文用SIMCA-P軟件對上證指數Y進行偏最小二乘回歸分析，輸入標準化數據進行成分提取，建立解釋變差表(表4)進行分析后，對模型成分個數進行選擇，可以得出模型成分數量為3時自變量可被解釋變差累計為96.9%，因變量可被解釋變差累計為81.7%，均處在較好水平，所以確定模型提取成分個數為3，建立模型如下：

Y=30.300+0.655X1+0.010X2+0.320X3+0.027X4-0.055X5+ε

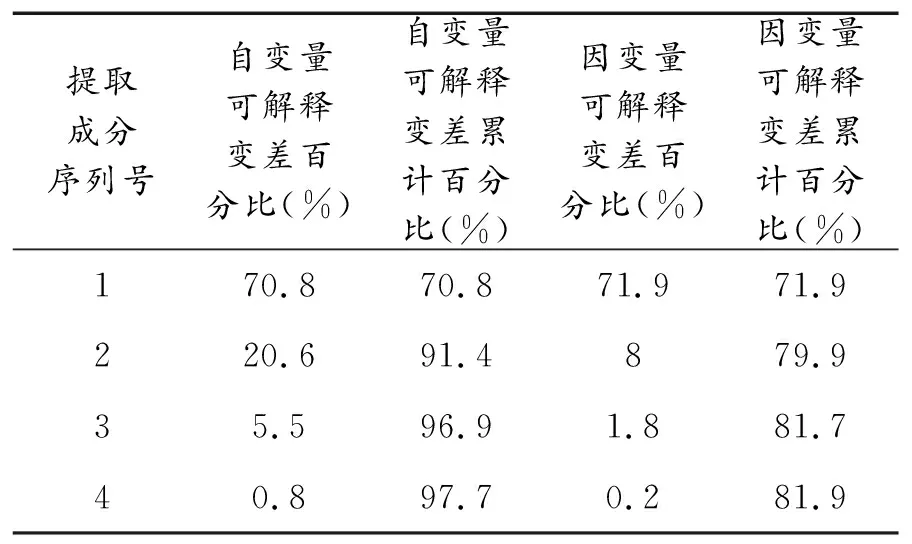
表4 解釋變差表

3.3.2 模型評價

得出模型結果為數據標準化后的模型，組合模型結果較單ARIMA模型得到較大修正，擬合優度由原本的0.71上升到0.82.

通過基于偏最小二乘方法的ARIMA組合模型對上證指數Y的后四期預測值與單ARIMA模型預測值對比(表5)可見，四個上證指數預測值殘差均有較大程度的減少，平均相對誤差值減少27.5%.這說明基于偏最小二乘方法的ARIMA組合模型預測值較單ARIMA模型預測值效果更好，使用偏最小二乘方法的組合修正模型能夠有效提高預測精度.

對模型中每個變量的重要程度作出分析：由于本文建立的模型為標準化模型，其系數只與影響方向有關，不能決定其影響大小；本文選取SIMCA-P軟件中的VIP統計量(圖6)對模型的每個變量重要程度作出分析，VIP統計量的值越大說明該變量的重要程度越高.由圖可見，自變量重要程度排名依次為X1、X3、X5、X4、X2；說明ARIMA(2,2,3)模型的預測結果對偏最小二乘回歸模型的結果影響最大.ARIMA模型在股票價格預測中通過添加相關變量做偏最小二乘回歸的方法可以有效提高預測精度.

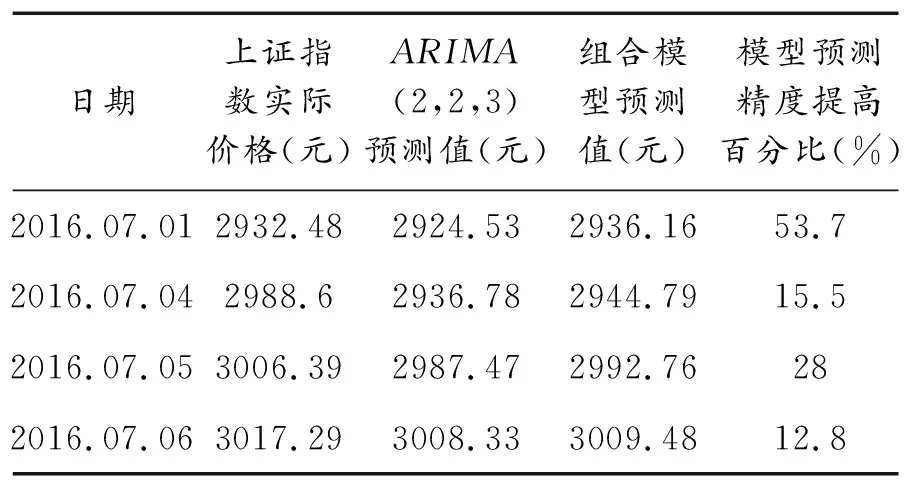
表5 組合模型預測結果

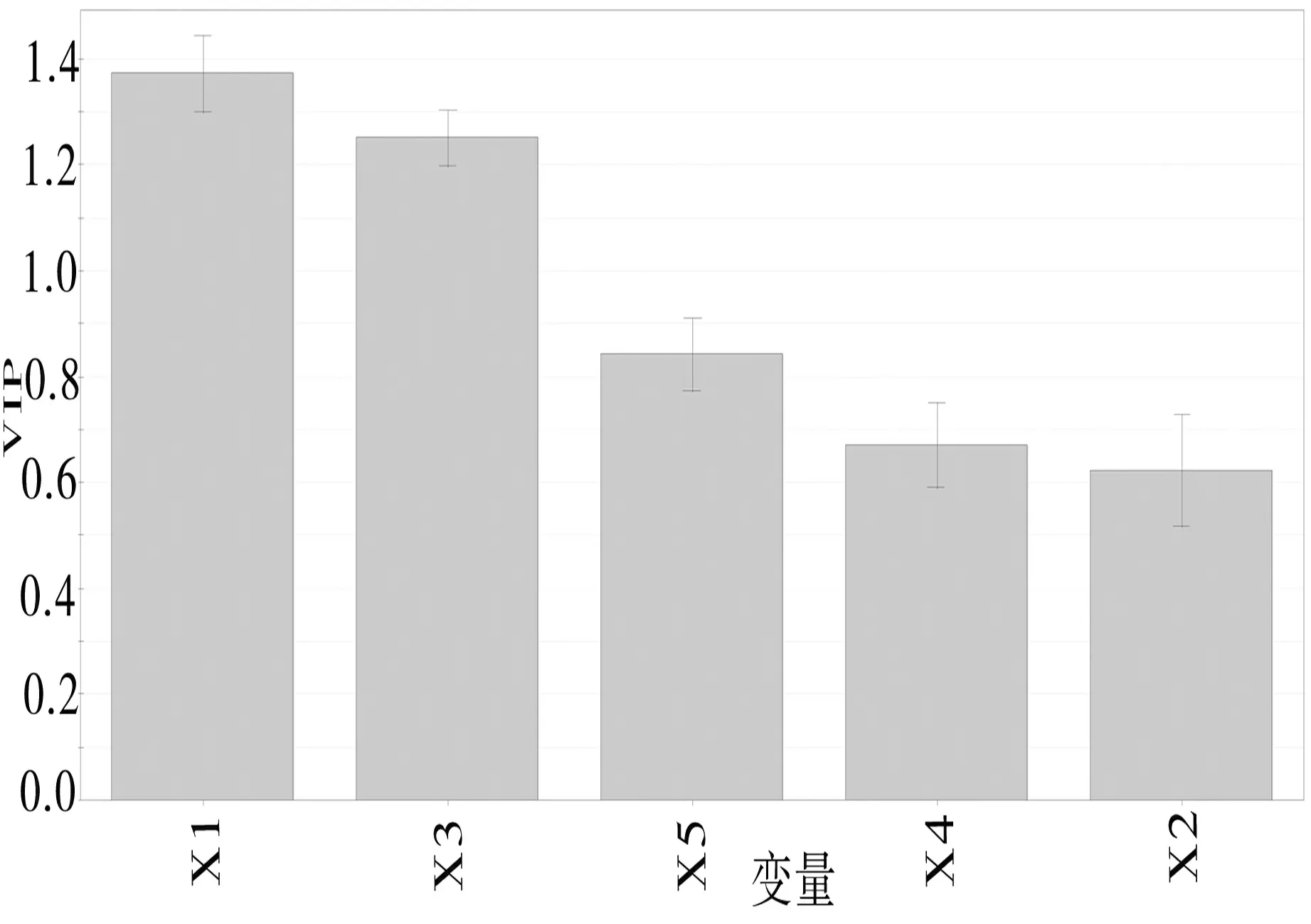
圖6 VIP統計量圖

結 論

本文首先在ARIMA模型對股票價格得出預測值的基礎上，根據偏最小二乘方法在股票類數據的相關性消除方面的優勢，引入ARIMA模型預測值作為因變量，再加入上一日交易量，上一日期貨價格，上一日美元對人民幣匯率，美國NASDAQ指數價格等變量，以上變量具有較強的相關性，通過偏最小二乘方法對其回歸建模，能得到較好的修正模型，有效提高模型精度.