60-110E半移動破碎站結構模態分析★

陳曉斌

（1.太原重工股份有限公司技術中心； 2.礦山采掘裝備及智能制造國家重點實驗室， 山西 太原 030024）

60-110E半移動破碎站是超重型破碎設備，適用于大型露天金屬礦山上礦石（巖石）的初級破碎。礦石（巖石）由汽車從采場運至半移動破碎站，經旋回式破碎機破碎后，由排料運輸機將其運至地表運輸機，進而將礦石（巖石）送到選礦廠或排土場。

旋回式破碎機是60-110E半移動破碎站的核心部件。它通過破碎機主軸的旋轉帶動內部動錐轉動，從而完成對礦石（巖石）的破碎。破碎機安裝于半移動破碎站的主體鋼結構上。正常工作情況下，旋回式破碎機主軸的轉速為151 r/min，即其工作頻率為2.52 Hz。

主體鋼結構由棧橋、吊車立柱、受料倉、破碎機平臺、排料倉、支撐、浮橋等部件組成。其用途主要是承載旋回式破碎機、液壓碎石機、旋臂起重機等部件。

工作過程中，60-110E半移動破碎站的主體鋼結構承受周期性變化的動載荷，因此，必須使其固有頻率遠離破碎機的工作頻率，保證其擁有足夠的整體剛度。

為了了解結構的振動特性和整體剛度，使用有限元軟件ANSYS對60-110E半移動破碎站進行模態分析就變得十分必要。

1 模態分析的定義

根據振動理論，模態是多自由度系統以某固有頻率振動時所呈現出來的振動形態。此時，系統內各點的位移具有一定的比例關系，稱為固有振型。無論阻尼如何，結構上各點對外載荷的響應都可以表示成由固有頻率、阻尼比和振型等模態參數組成的各階振型模態的疊加。

模態分析在動力學分析過程中用于確定設計中的結構或機器部件的振動特性，即結構的固有頻率和振型。它們是承受動態載荷作用的結構的重要參數。

2 模態分析的基本原理與方法

模態分析是求系統的自振頻率和振型的過程。無阻尼自由振動結構的運動方程可寫成如下矩陣形式：

式中：[M]為質量矩陣；[K]為剛度矩陣；{ü}為加速度向量；{u}位移向量。

對于線性系統而言，自由振動具有以下簡諧形式：

式中：ωi為第 i階自振頻率；{φ}i為第 i階自振頻率所對應的模態向量；t為時間。

將式（2）代入式（1），即可得：

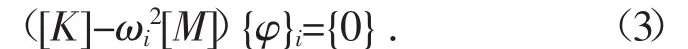
[K]-ωi2[M]稱為特征矩陣。

要使式（3）有解，必須使其系數行列式為零：

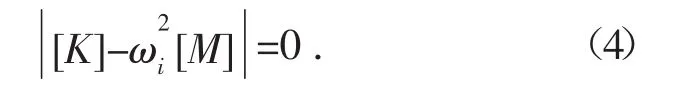
式（4）稱為系統的頻率方程或特征方程。由此可以求出n個特征根ωi2。

將每個特征根ωi代入式（3），可求出相應的模態向量{φ}i。

具有最低頻率的振型叫做第一振型，具有第二低頻率的振型叫做第二振型，以此類推。

在有限元軟件ANSYS中，有多種對動力學模型的模態提取方法。本次模擬采用的Block Lanczos模態提取法。

Lanczos模態提取法能有效逼近結構離散化模型的低維模態空間，該方法可以利用Lanczos矢量矩陣來實現系統數學模型的降階，使得更簡便地求出系統的低階固有特性[1]。

振動特性是反映結構動力響應的重要參數。它不受外加荷載的影響，僅與結構本身的形式、尺寸、材料有關。模態分析可以確定結構的振動特性，包括自振頻率、周期和振型。

運用模態分析法，可以不必去求出所有的固有頻率及其所對應的振型，只求解所需要的階次模態來建立相應的計算模型。這對工程的實際應用已有足夠參考價值。通常來說，結構的前幾階固有頻率對振動的貢獻最大。因此，在實際計算中，只要考慮那些貢獻較大的模態已經可以滿足實際工程的需要。

3 破碎站主體鋼結構模態分析

為了防止結構發生共振，對破碎站的主體鋼結構進行模態分析。

模態分析包括四個步驟，即建立模型，添加載荷并求解，擴展模型模態，察看分析結果和后處理[2]。

在ANSYS中，采用Block Lanzos法對破碎站鋼結構進行模態分析，計算結果如表1所示。

從表1顯示，破碎站鋼結構的各階次自振頻率均大于或等于3.37。

表1 破碎站鋼結構第一階至第四階的自振頻率計算結果

通過擴展振型可以獲得主體鋼結構各階次自振頻率的振型圖（見圖1—圖4）。

由圖1—圖4可以看出，破碎站鋼結構的第一、二階模態振型為吊車立柱及上部結構平動，第三下部斜支撐連接板局部振動，第四階振型表現為吊車立柱彎曲振動。

4 結論

1）從模態分析的計算結果可知，破碎站鋼結構的各階次自振頻率均大于或等于3.37，均距破碎機的工作頻率2.52 Hz較遠，基準自振頻率3.37 Hz比破碎機的工作頻率大33.7%，故可判定破碎站主體結構不會發生共振現象。

圖1 第一階振型圖（吊車立柱及上部結構Y向平動）

圖2 第二階振型圖（吊車立柱及上部結構X向平動）

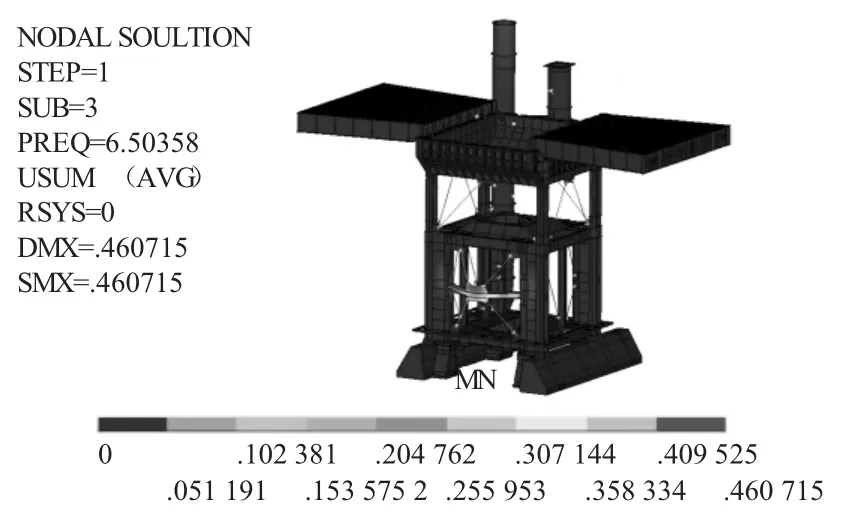
圖3 第三階振型圖（下部斜支撐連接板局部振動）

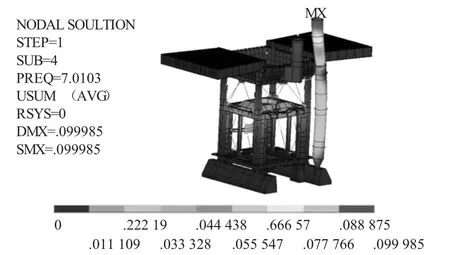
圖4 第四階振型圖（吊車立柱Y向彎曲振動）

2）通過各主要階次自振頻率的振型圖可以看出，吊車立柱的振動主要是彎曲振動，其他部分主要是以平動為主。這表明主體鋼結構的整體剛度足夠大，結構的整體布置較為合理，對系統在動力荷載作用下的受力形態較為有利。