一種改進的THz-SAR高頻振動誤差補償方法

， ， ，

( 1.上海無線電設備研究所， 上海 200090； 2.上海目標識別與環(huán)境感知工程技術研究中心， 上海 200090)

0 引言

太赫茲波通常指頻率在0.1～10 THz之間的電磁輻射，波長為3 mm～30 μm。從頻率上看，太赫茲波介于毫米波與紅外光之間；從能量上看，太赫茲波介于電子和光子之間。由于太赫茲波的特殊性質，將其用于合成孔徑雷達成像可以打破傳統(tǒng)光學雷達和毫米波雷達成像的諸多瓶頸。與光學雷達相比，太赫茲合成孔徑雷達(Terahertz Synthetic Aperture Radar，THz-SAR)具有高透射性，能穿透介質材料探測隱蔽物體，可用于安檢、質檢領域；與微波、毫米波雷達相比，THz-SAR分辨率高、對目標微動敏感，可用于微動目標檢測等領域[1-4]。因此，THz-SAR成像技術已成為當前太赫茲領域的重要研究方向之一。

微波SAR中，常見的運動誤差分為位置誤差和姿態(tài)誤差。通常，姿態(tài)誤差可采用天線伺服平臺控制波束指向，穩(wěn)定飛行姿態(tài)，對成像結果影響較小；而位置誤差會導致回波信號包絡和相位的畸變，對成像結果影響較大，需重點補償。低頻段的相位誤差主要來源于航向速度、加速度及視線加速度的誤差，三者的限制條件都與波長成反比，而高頻段相位誤差的限制條件均與波長成正比[5]；并且THz-SAR平臺的高頻振動誤差雖然振幅很小不會影響航跡，卻會嚴重影響回波相位，使成像結果惡化，而現(xiàn)有運動傳感器也尚未達到檢測毫米級高頻振動誤差的精度[6]。因此THz-SAR對高頻振動誤差的補償要求更高。

關于THz-SAR高頻振動誤差補償算法，很多學者已給出一些研究成果。文獻[6]針對太赫茲視頻SAR高頻振動誤差提出一種結合運動傳感器、光學隔振平臺和回波數(shù)據自聚焦于一體的三級運動補償法，但光學隔振平臺體積較大，不方便安裝于機載平臺且價格較貴。文獻[7]提出了基于回波數(shù)據的THz-SAR運動補償方法，仍然應用了隔振平臺。文獻[8-9]采用參數(shù)化自聚焦實現(xiàn)THz-SAR振動補償，對振動頻率的估計采用了短時傅里葉變換(STFT)，但該方法存在分辨率單一、高頻分辨率低且無法同時達到時間、頻率分辨率最優(yōu)等問題。文獻[10]采用小波變換對常規(guī)SAR中振動目標參數(shù)進行估計，與STFT方法相比，小波變換在高頻處的分辨率更高，具有更大的頻率估計范圍。本文采用改進的多普勒Keystone變換(Doppler Keystone Transform，DKT)方法實現(xiàn)THz-SAR成對回波的聚焦成像，引入小波多分辨分析進行平臺振動頻率估計，可以實現(xiàn)平臺高頻振動頻率下的精確估計，再結合參數(shù)空間投影法估計振動幅相實現(xiàn)THz-SAR高頻振動誤差的精確補償，能有效提升THz-SAR平臺實際成像質量，最后采用點目標仿真證明了上述結論。

1 幾何模型

現(xiàn)有研究表明，機載THz-SAR平臺沿雷達視線方向(LOS)的高頻振動對成像有影響，而垂直視線方向的高頻振動對成像的影響可以忽略不計[6]。設機載THz-SAR成像幾何模型如圖1所示，建立坐標系OXYZ，平臺在距地面高度h處沿Y軸方向水平飛行，工作于正側視觀測模式，速度大小為va，下視角為θL。考慮平臺高頻振動為單頻的情況，并且近似為簡諧振動。若平臺無振動時的瞬時相位中心位于C點，平臺有振動時的瞬時相位中心在LOS方向的投影為C′點，則t時刻，平臺在LOS上的瞬時振動偏移量r(t)(即CC′)可表示成

r(t)=Avsin2πfvt+φv

(1)

式中，Av，fv，φv分別表示該高頻振動分量的振幅、頻率及初相。定義當fv·Ta≥1時，雷達平臺的振動頻率屬于高頻，Ta表示合成孔徑時間。

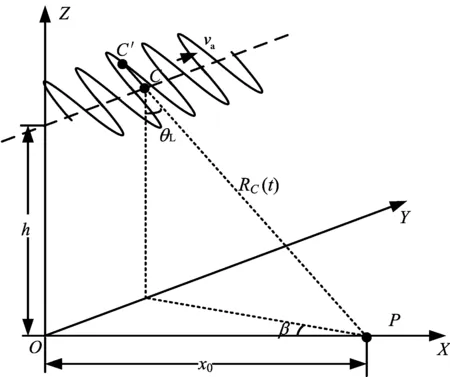
圖1 機載平臺振動成像幾何模型

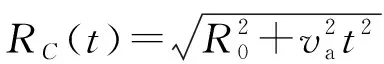
Avsin2πfvt+φv

(2)

易知，回波信號的瞬時多普勒頻率表達式為

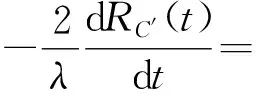
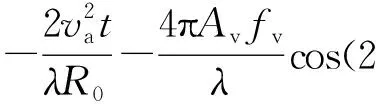
(3)

由式(3)可知，THz-SAR平臺的高頻振動在多普勒頻率表達式中引入了一系列正弦調制的頻率成分，其大小與高頻振動的振幅、頻率、初相等有關。

2 信號模型

假設雷達發(fā)射線性調頻信號，平臺接收的回波信號經脈沖壓縮后表示為[11]

式中，fτ為距離頻率，t為方位時間，Wr(·)為距離頻譜的包絡，wa(·)為方位時域包絡，t0為波束中心穿越時刻，f0為雷達載頻，c為光速。

對式(4)進行Bessel級數(shù)展開，再變換到兩維頻域，得到[11]

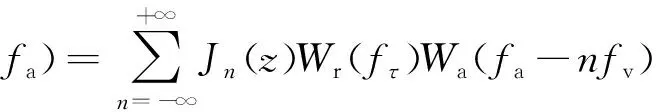
exp-j2π(fa-nfv)t0expjnφv+π·

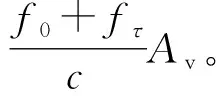
式(5)的最后一個相位項中，第二、三項分別表示距離走動和距離彎曲，第四項表示平臺振動引入的相位項，在窄帶假設下，滿足f0?fτ，近似成

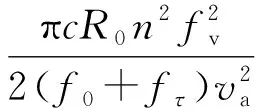
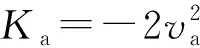
采用文獻[11]中基于DKT的成像算法對式(5)信號進行處理，流程圖如圖2所示，主要分為4個步驟，即距離走動校正、距離徙動校正、方位二次相位補償以及剩余視頻相位(RVP)消除(每步的詳細操作參見文獻[11])。最終得到THz-SAR成像結果如式(7)[11]所示。

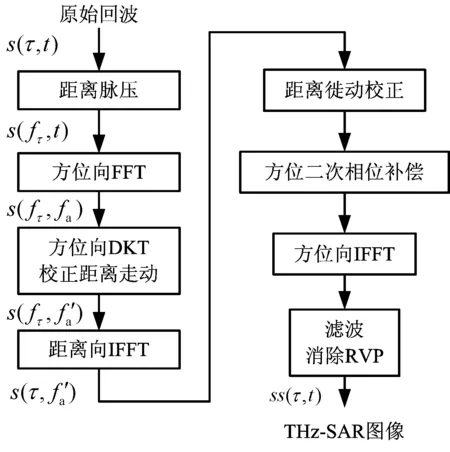
圖2 DKT成像算法流程圖

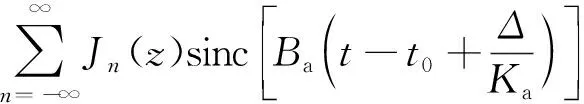
expjn2πfvt+φv+π·

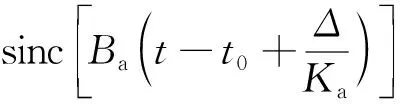
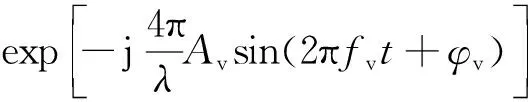
式中，sinc·表示辛克函數(shù)，Br表示發(fā)射信號帶寬，Ba表示信號的多普勒帶寬。

式(7)的第一項sinc函數(shù)表示SAR成像結果的方位向聚焦情況，其中包含與平臺振動有關的時間序列項Δ/Ka(Δ=nfv)，意味著最終SAR圖像中目標真實位置的兩側會存在周期性分布的成對回波，且相鄰回波的時間間隔為Tfv=fv/Ka。成對回波的產生與平臺振動有關，因此需要準確估計平臺振動參數(shù)，從而抑制成對回波。

3 振動參數(shù)估計

式(7)中，第一、二項均與振動參數(shù)有關，首先將式(7)變換回距離多普勒域：

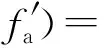
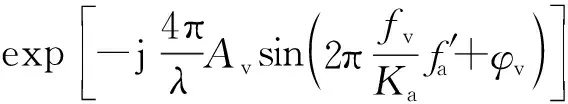
式(8)中，振動參數(shù)都包含在相位里。由于相位里的正弦信號項(高頻)數(shù)值遠小于R0項(低頻)，若此時直接取式(8)相位進行傅里葉變換，則變換后振動信號的頻譜與低頻部分相比，會因幅度太小而無法精確獲知[10]。

傅里葉變換只在頻域中具有較好的分析能力，考慮對式(8)的相位項進行時頻分析來區(qū)分低頻、高頻信號。短時傅里葉變換(STFT)是經典的時頻分析方法之一，它在傅里葉變換的基礎上增加一個固定的時域窗函數(shù)對信號作分段分析，但該方法存在分辨率單一、高頻分辨率差等諸多缺陷。小波變換可以克服STFT分辨率單一的問題，能夠聚焦信號的任意局部細節(jié)，本文提出基于小波多分辨分析(Multi-Resolution Analysis，MRA)結合參數(shù)空間投影的方法，實現(xiàn)振動參數(shù)的精確估計，信號處理流程如圖3所示。

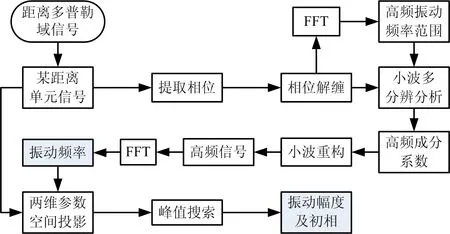
圖3 振動參數(shù)估計方法總流程

3.1 小波多分辨分析的振動頻率估計

小波多分辨分析特性是由Mallat和Meyer于1986年提出的，1989年Mallat又據此構造了Mallat算法，即小波基函數(shù)分解與重構快速算法。小波多分辨分析的示意圖如圖4所示。

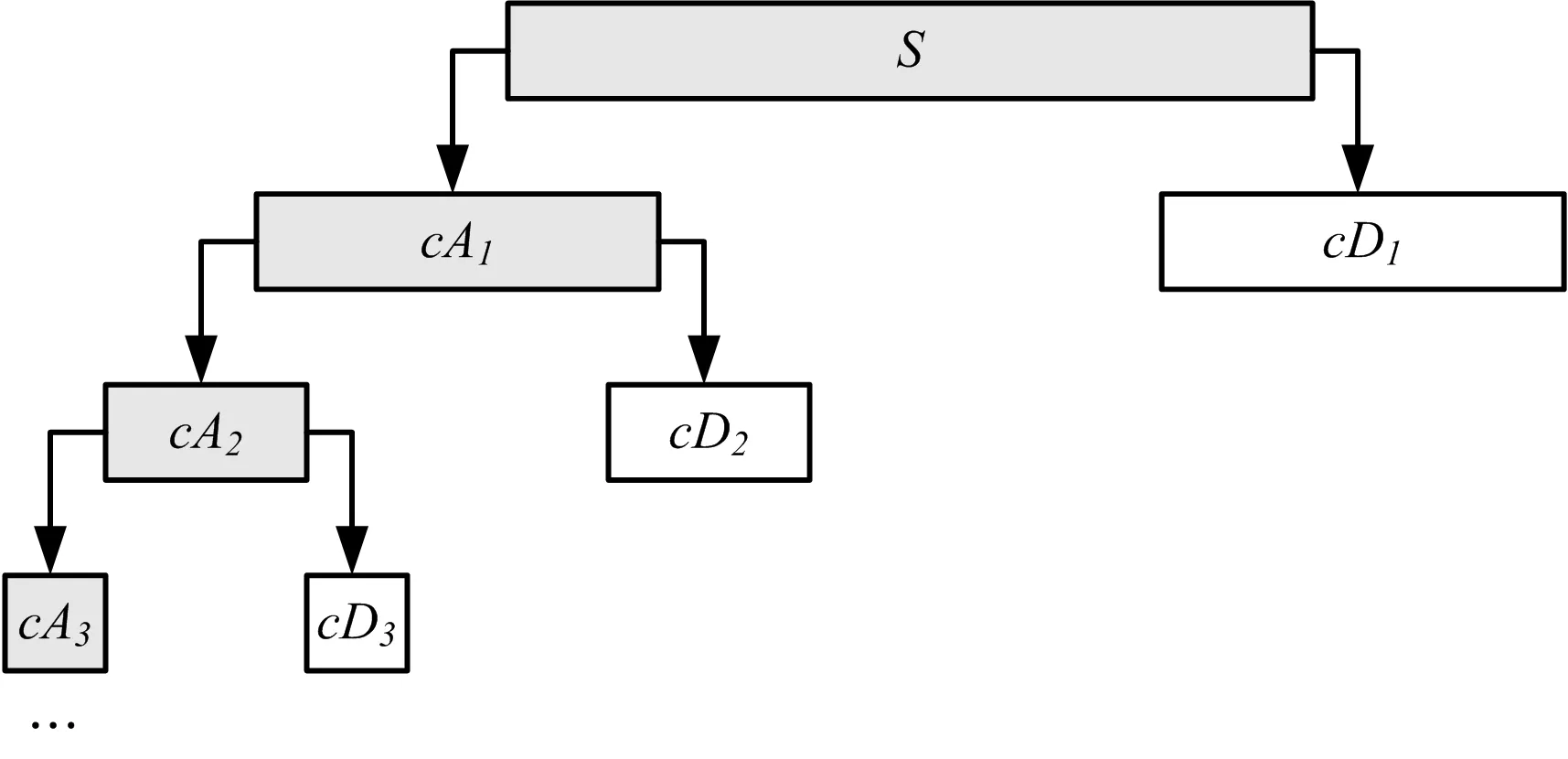
圖4 小波多分辨分析分解示意圖

圖4中，S表示原始信號，每層分解都將信號分解為低頻部分cAi和高頻部分cDi，然后再對低頻部分繼續(xù)向下分解，得到低頻部分和高頻部分，依此類推。在i層分解后所得各分量與原始信號S的關系可表示為

S=cAi+cDi+cDi-1+…+cD1

(9)

若原始信號S的采樣頻率為fS，那么第i層分解的低頻分量、高頻分量所代表的頻率范圍分別為0～fS/2i,fS/2i～fS/2i-1。因此，根據感興趣的頻率范圍可以確定小波多分辨分析的分解層數(shù)，并且提取相應頻率成分的小波系數(shù)，通過小波重構恢復出該頻率范圍的信號，實現(xiàn)不同頻率信號的分離。

提取式(8)相位，經相位解纏后的表達式為

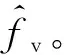
3.2 參數(shù)空間投影的振動幅度和初相估計

將式(8)信號向該參數(shù)空間投影，即

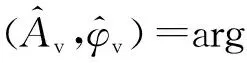
(13)

(14)

將式(8)與式(14)相乘，實現(xiàn)高頻振動補償，再作方位向IFFT變換回到兩維時域：

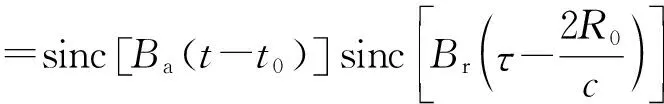
可見，回波信號在距離向與方位向均呈現(xiàn)sinc函數(shù)的形式，意味著在THz-SAR平臺高頻振動下對點目標實現(xiàn)了兩維聚焦成像。

4 實驗仿真

首先采用基于DKT的THz-SAR成像算法對點目標進行成像，表1給出系統(tǒng)仿真參數(shù)。仿真中在場景中心處設置了一靜止點目標。

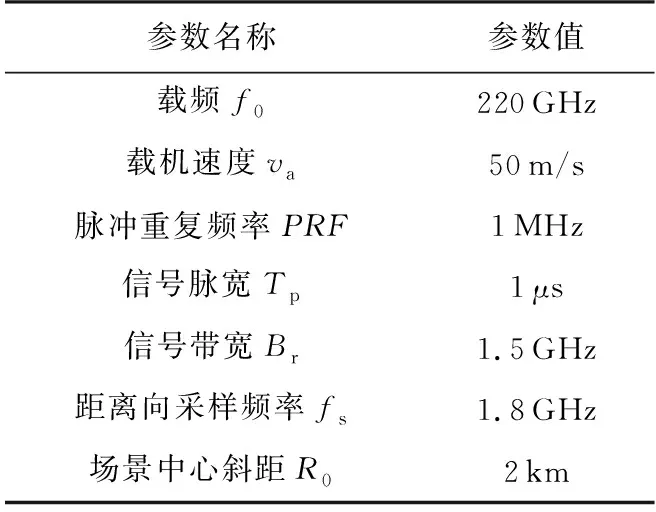
表1 系統(tǒng)參數(shù)表

根據文獻[5]中給出的THz-SAR系統(tǒng)高頻振動幅度誤差限制條件：

結合表1參數(shù)計算出不影響THz-SAR成像的高頻振動幅度Av≤1.7×10-4m，而以下仿真均考慮雷達平臺沿LOS方向的高頻振動，因此選取LOS方向振動幅度Av=1×10-3m來進行驗證。

1) 基于DKT的THz-SAR成像質量分析

考慮THz-SAR平臺單一頻率的高頻振動情況，假設fv=20 Hz,φv=π/4，得到點目標的成像結果如圖5所示。圖5(a)、圖5(b)分別是RVP消除前后距離多普勒域信號的形式，可見，上述基于DKT的THz-SAR成像算法實現(xiàn)了距離單元徙動的準確校正，使得點目標的主回波以及成對回波得以聚焦成像，而RVP校正也是為了便于后續(xù)的振動參數(shù)估計。圖5(c)是THz-SAR成像結果，顯而易見，點目標在方位向上存在周期性成對回波。

為了更直觀地檢驗成對回波聚焦質量，采用矩形窗截取圖5(c)中第126個方位單元處的點目標，四倍升采樣后，所得結果的兩維剖面如圖6所示。由兩個剖面圖可以看出，其方位向和距離向的輸出分辨率分別為0.087 5 m和0.104 2 m，峰值旁瓣比分別為-13.22 dB和-13.16 dB，積分旁瓣比分別為-10.29 dB和-12.59 dB。已知方位向和距離向的理論分辨率為0.086 5 m和0.100 0 m，因此，點目標兩側較遠的成對回波也能聚焦良好。

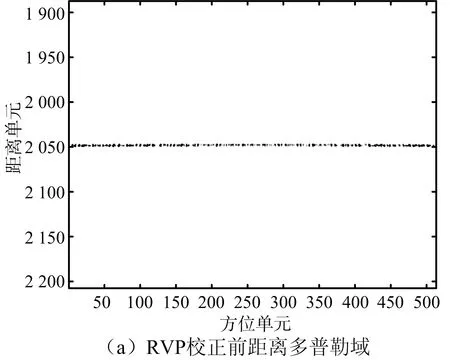
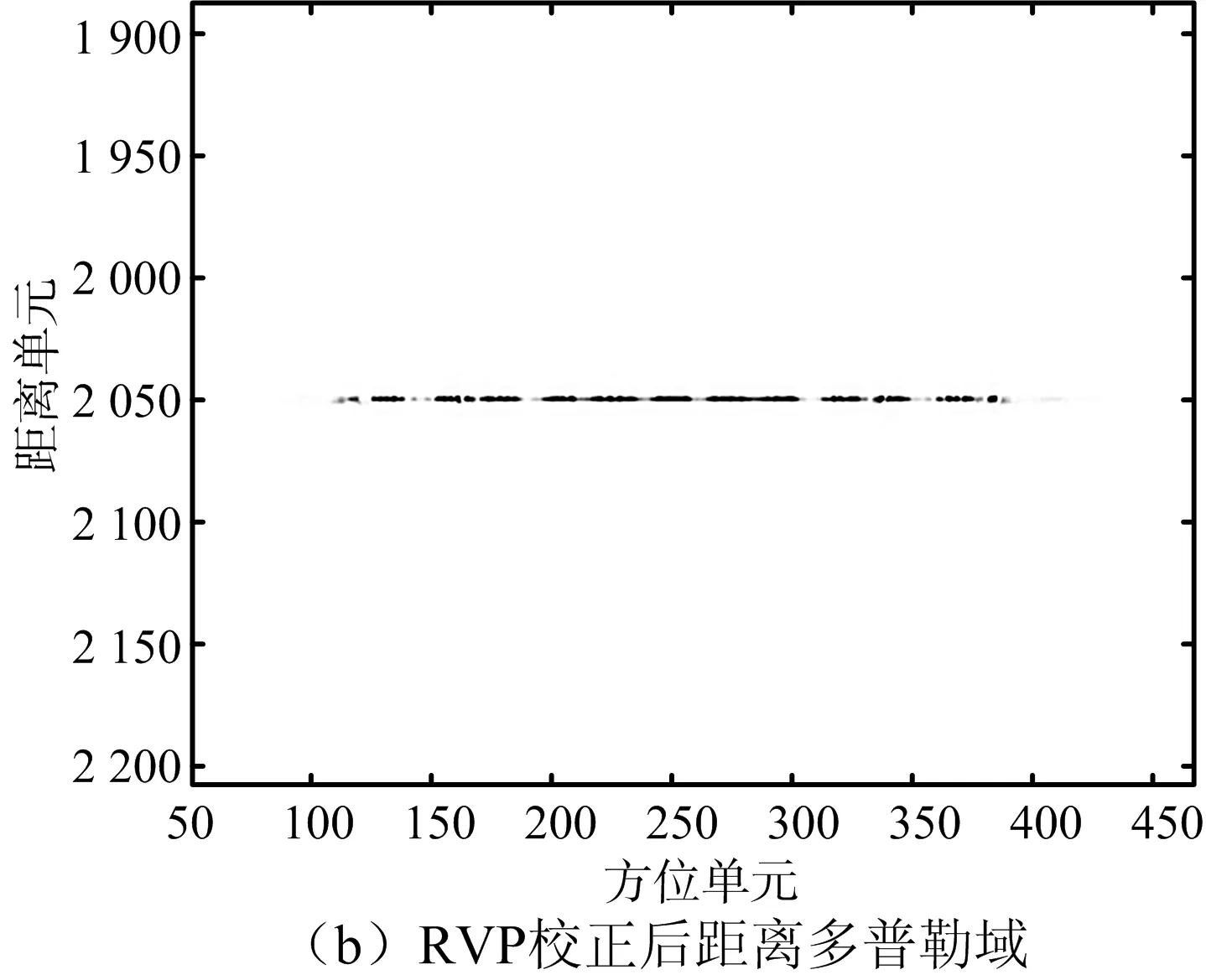
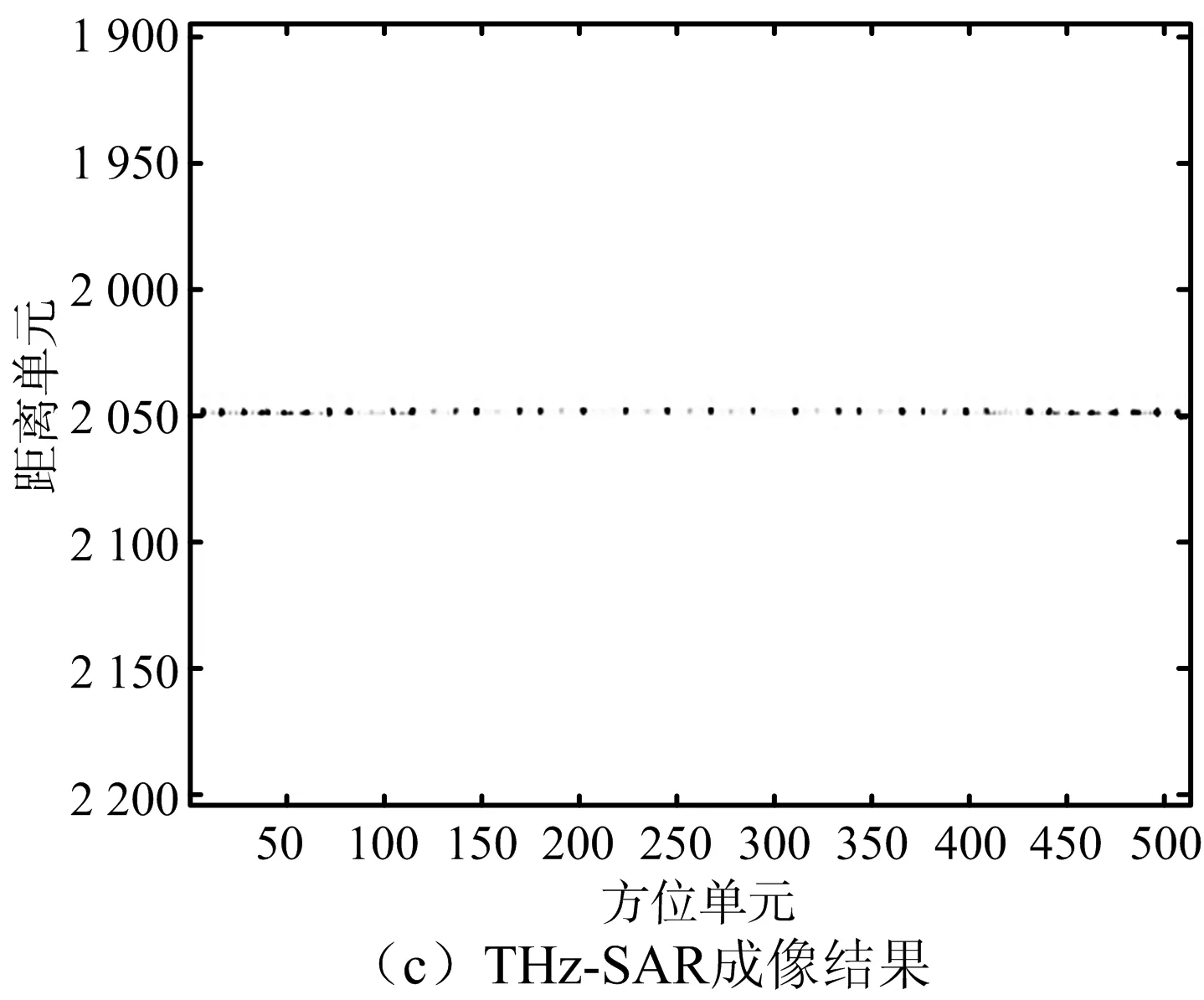
圖5 平臺高頻振動下的成像結果

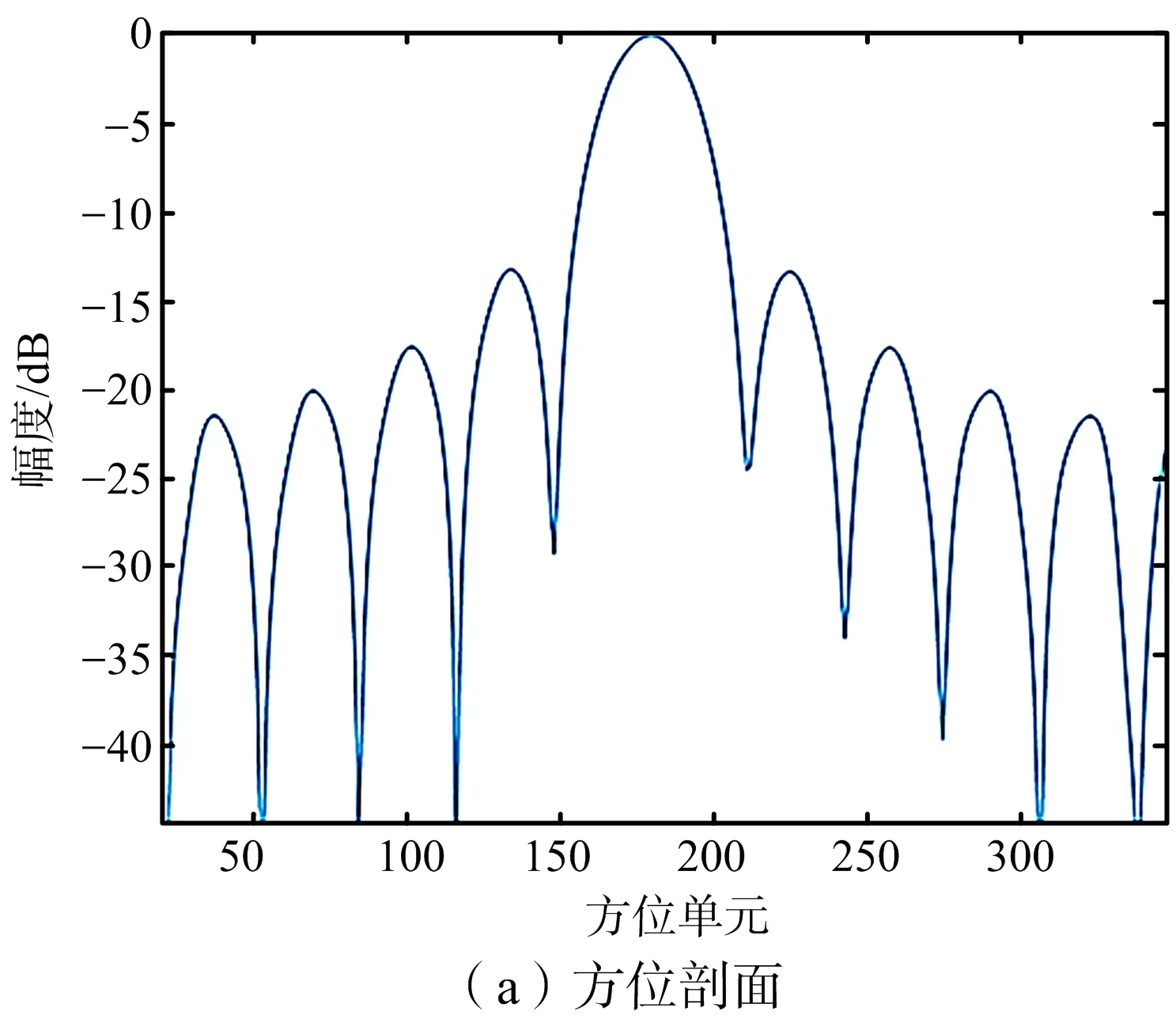
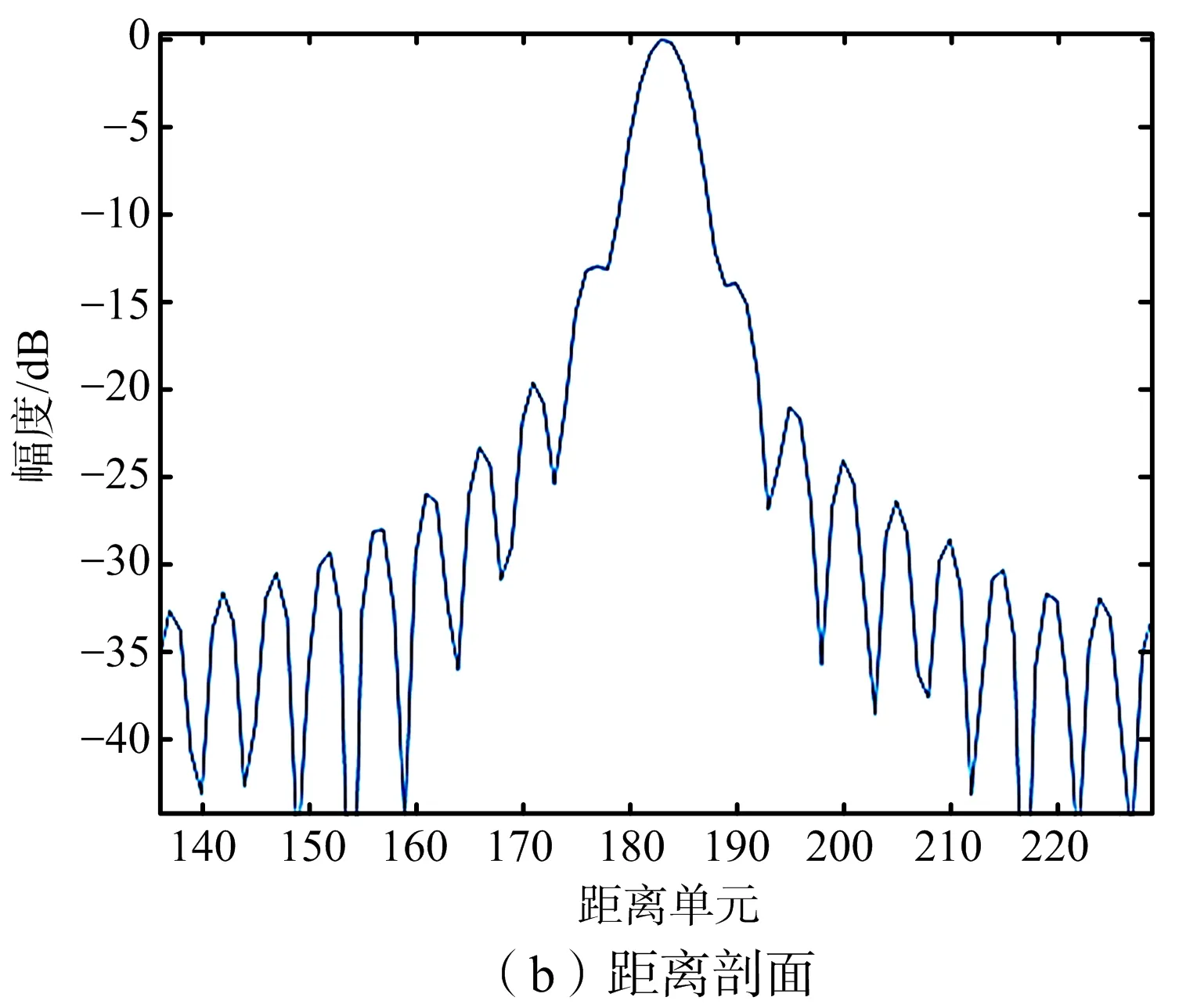
圖6 成對回波成像質量分析

2) 平臺振動參數(shù)估計

在成對回波聚焦成像后，需要對成對回波進一步抑制，也即通過振動參數(shù)估計和補償來完成THz-SAR最終成像。仿真中，考慮平臺在兩種不同振動頻率fv1=20 Hz和fv2=40 Hz下，各自小波多分辨分析的頻率估計效果，以及基于STFT時頻分析的頻率估計效果，進行對比試驗。

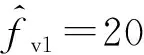
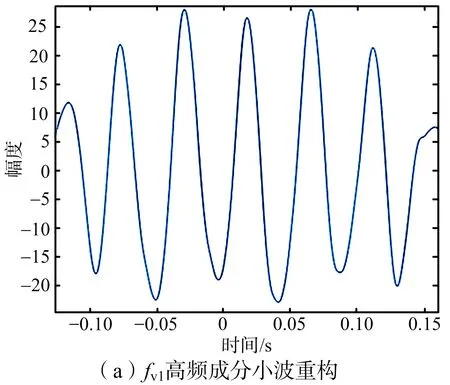
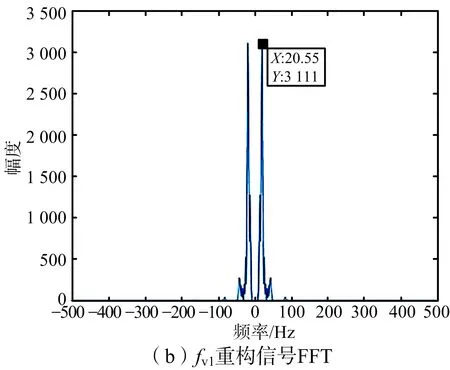
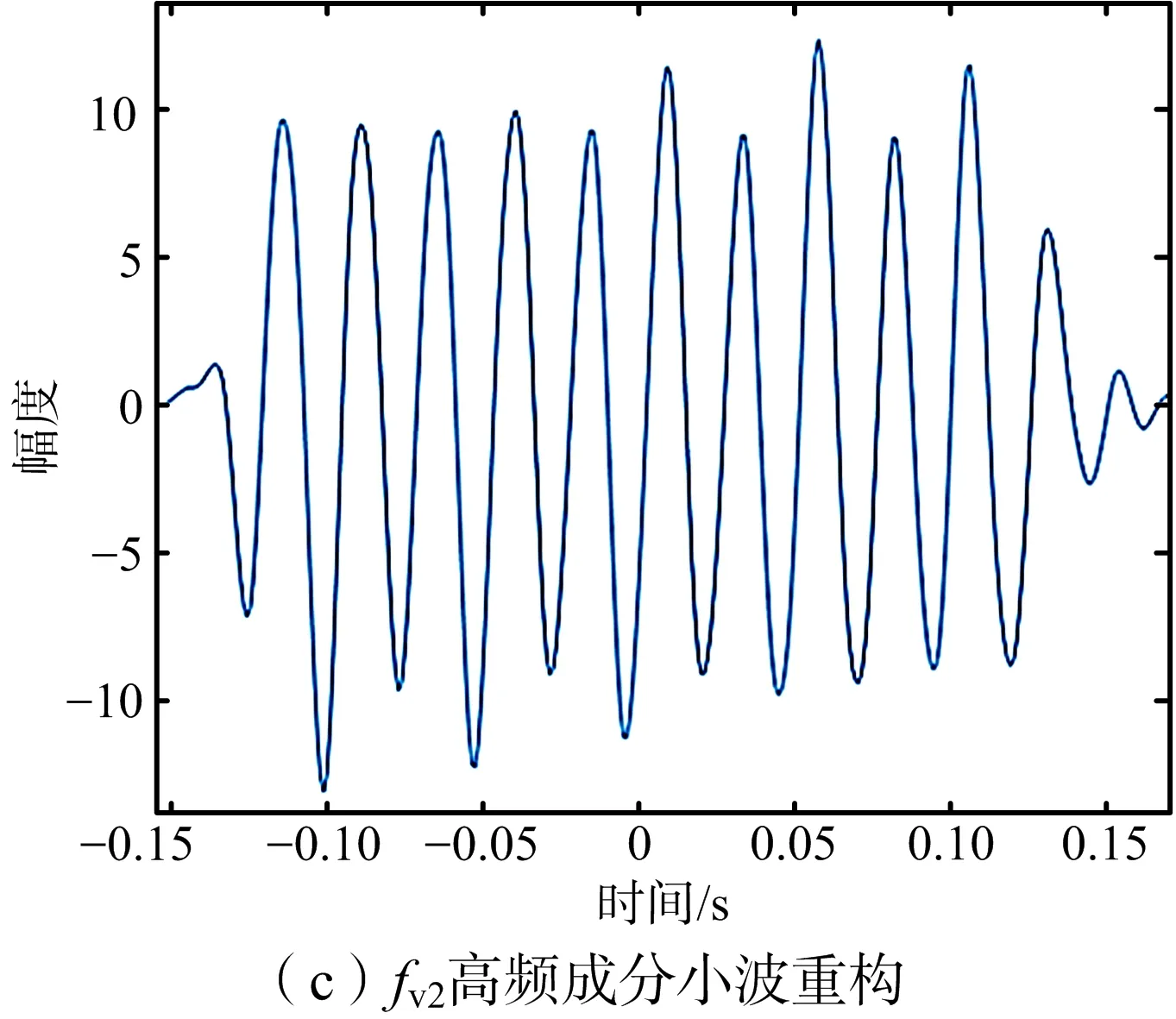
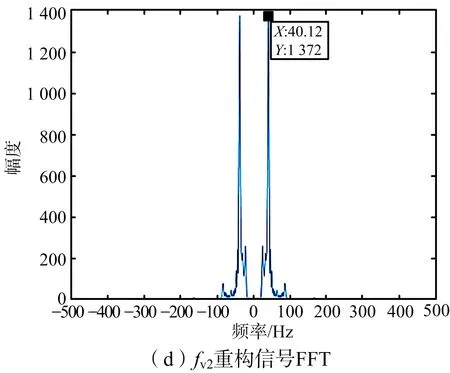
圖7 小波MRA振動頻率估計結果

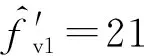
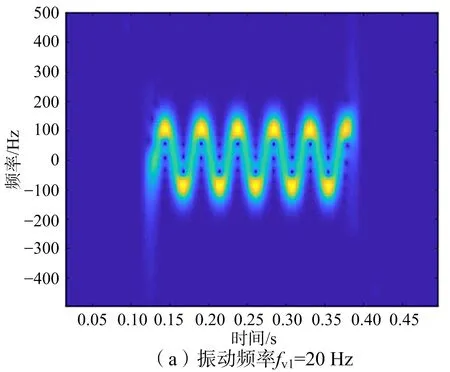
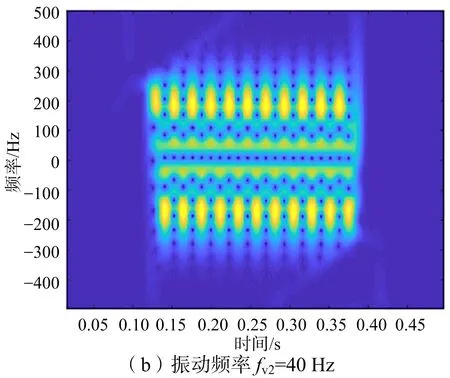
圖8 STFT時頻分析圖

圖9 參數(shù)空間投影的幅相估計

3) 成對回波抑制

根據式(14)利用平臺振動參數(shù)估計值構造補償函數(shù)，對THz-SAR初步成像結果進行高頻振動誤差補償，得到成對回波抑制后的THz-SAR成像結果，如圖10(a)所示。圖10(b)、圖10(c)給出了點目標所在距離單元成對回波抑制前后的方位剖面圖，明顯可見THz-SAR平臺高頻振動導致的成對回波得到了有效抑制，點目標的真實位置清晰地顯現(xiàn)出來，仿真結果證明了本文算法的可行性。

最后采用多點目標進行算法驗證，圖11(a)、圖11(b)分別為成對目標抑制前后多點目標的THz-SAR成像結果。可知，基于小波MRA的振動參數(shù)估計算法對方位向多個點目標存在的情況仍然適用，多個點目標疊加的距離多普勒域信號采用本文算法處理依然能得出平臺振動參數(shù)，從而實現(xiàn)成對回波的有效抑制。

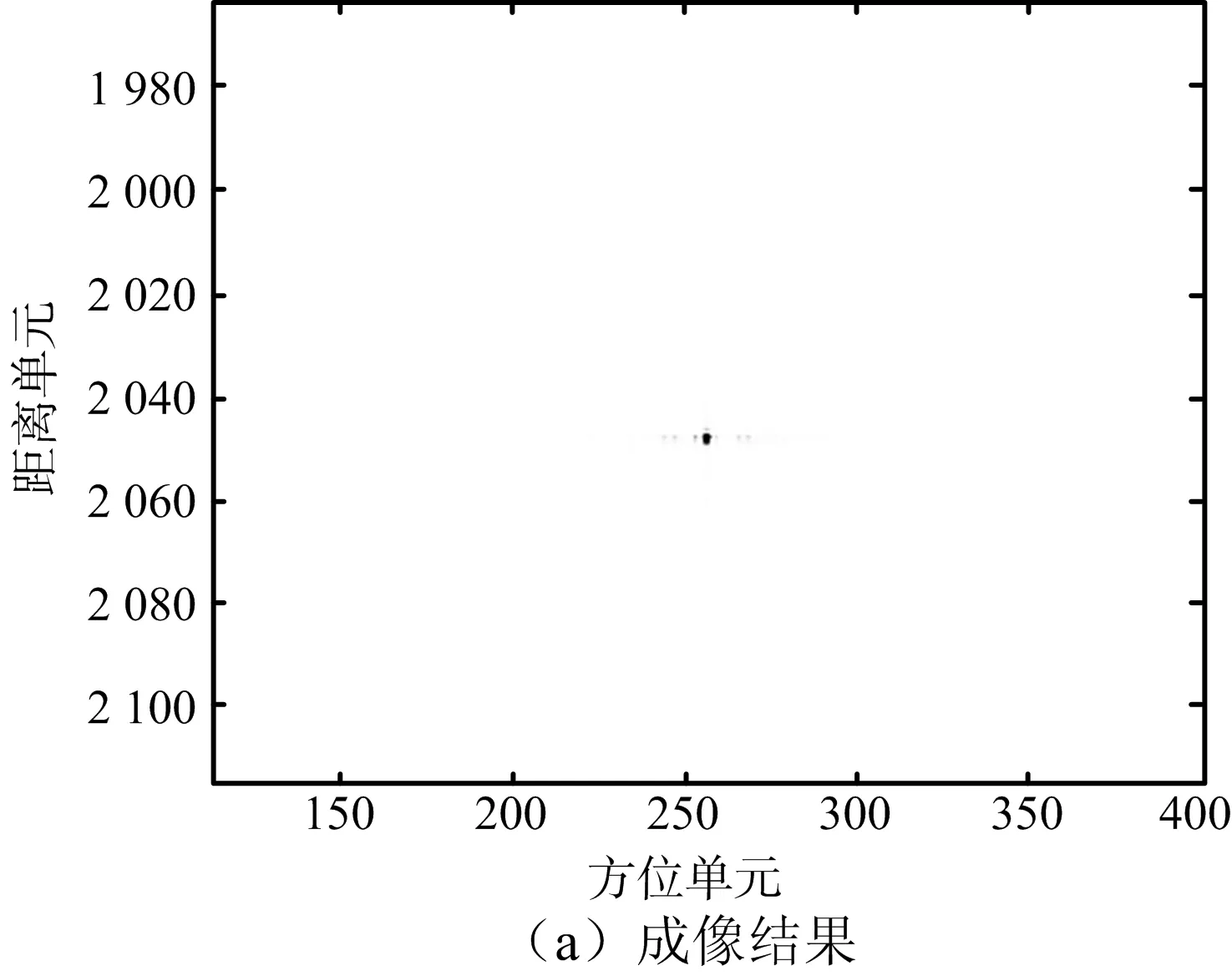
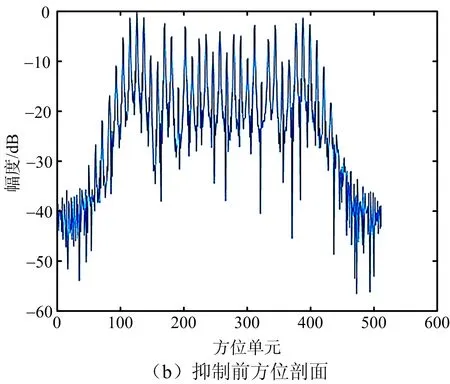
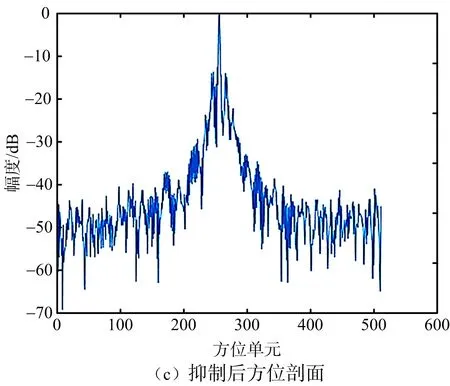
圖10 平臺振動下成對回波抑制前后對比

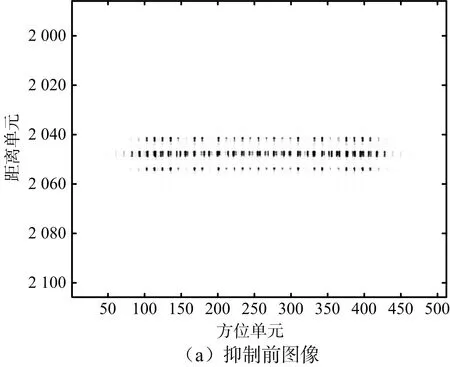
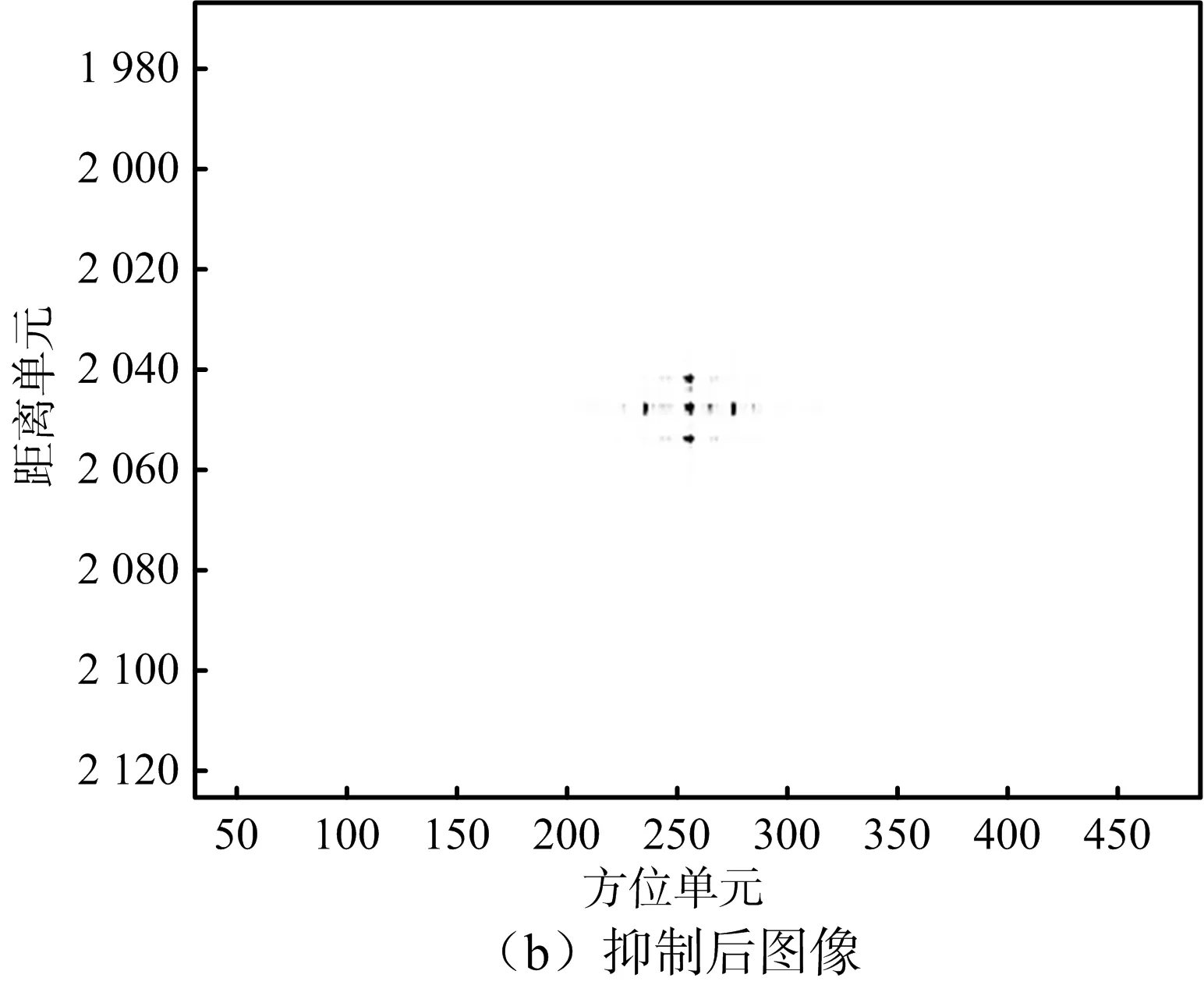
圖11 多點目標成對回波抑制結果

5 結束語

高頻振動誤差是THz-SAR成像中需要特殊考慮的運動誤差形式，會在SAR圖像中引入成對回波現(xiàn)象。針對該運動誤差，傳統(tǒng)SAR成像算法無法實現(xiàn)成對回波的聚焦，從而直接影響到高頻振動誤差的補償效果。因此，本文采用基于DKT的THz-SAR成像算法，結合小波多分辨分析以及參數(shù)空間投影方法，對THz-SAR平臺的高頻振動參數(shù)作出有效估計，實現(xiàn)精確運動補償。文中采用計算機仿真驗證了算法的正確性，最終得到了高頻振動THz-SAR平臺下的聚焦點目標像。該方法為實際THz-SAR成像應用中的運動補償提供了可行方案，具有一定參考性。實際中，THz-SAR平臺的高頻振動可能會包含多種頻率成分，因此后續(xù)需要進一步研究THz-SAR平臺處于多頻振動等更復雜情況下的運動誤差補償方法。