粒子群算法修正測距的 無線傳感器網絡節點定位

樓國紅, 張劍平

(太原工業學院 電子工程系, 太原 030008)

無線傳感器網絡由自治無線節點構成, 這些節點隨機部署在一個區域, 對控制對象的參數進行收集, 如溫度、 聲音、 電壓等, 以幫助管理人員快速、 及時地收集對象數據. 節點定位是無線傳感器網絡的應用基礎, 如果節點位置信息無效或錯誤, 則無線傳感器網絡無法對目標進行準確、 實時監控, 因此節點定位方法的設計與研究是該領域關注的焦點[1-3].

目前, 節點定位常采用全球定位系統(global positioning system, GPS)對節點的位置進行計算, 該方法受外界環境干擾小、 實時性好、 魯棒性高, 是目前定位精度最高的一種方法[4]. 無線傳感器網絡由大量的節點組成, 如果每個節點安裝一個GPS, 會導致無線傳感器網絡定位的成本高, 因此通常對少量的無線傳感器網絡節點安裝GPS, 其位置已知, 這些節點稱為錨節點[5]. 先將錨節點的位置作為參考信息, 再對其他未知節點的位置進行估計和定位, 當前無線傳感器網絡節點定位算法根據是否需要硬件支撐情況劃分為兩類： 測距的無線傳感器網絡定位算法和無需測距的無線傳感器網絡定位算法[6]. 測距的無線傳感器網絡定位算法需要額外硬件支持, 根據信號強度或角度信息對無線傳感器網絡的節點位置進行估計, 如基于信號接收強度指示的無線傳感器網絡定位算法, 其傳感器節點定位精度高, 定位成本也相對更高. 而無需測距的無線傳感器網絡定位算法不需要額外硬件支持, 工作過程相對簡單, 已成為當前無線傳感器網絡的主要研究方向[7-9]. 無需測距的無線傳感器網絡定位算法主要有質心定位算法和DV-Hop算法. 質心定位算法根據無線傳感器網絡的連通性和未知節點不斷接收到的錨節點發送信息進行定位, 但其定位誤差較大, 無法準確確定未知節點的位置. 為了解決質心定位算法的缺陷, 文獻[10-12]將測距中的到達時間差定位算法與其進行組合, 對其定位結果進行加權, 一定程度上提高了節點的定位精度, 但權值如何進行確定沒有統一的標準和理論指導, 定位結果并非真正的最優. DV-Hop定位算法根據錨節點與未知節點之間的跳距實現節點定位, 因此節點距離的估計最關鍵, 標準DV-Hop定位算法采用平均距離作為節點距離, 當無線傳感器節點的分布不均勻時, 測距值估計的距離較大, 從而導致傳感器節點的定位誤差較大. 文獻[13]提出了采用遺傳算法對測距進行優化和修正, 減少平均測距誤差, 但遺傳算法存在收斂速度慢, 進化后期易出現停滯現象, 難得到局部最優解, 對測距優化結果產生不利影響, 最終對無線傳感器網絡的節點定位結果進行干擾.

針對節點定位存在的問題, 本文設計一種基于粒子群修正測距的無線傳感器節點定位算法. 首先對DV-Hop的工作原理進行分析, 找到導致跳距估計誤差的因素, 然后采用粒子群算法對無線傳感器節點之間的測距估計結果進行修正, 以減少節點間的測距估計誤差, 并對標準粒子群算法的不足進行相應的改進, 最后通過仿真實驗與當前經典無線傳感器節點定位算法進行對比測試. 測試結果表明, 在相同工作環境下, 本文方法提高了無線傳感器節點的定位精度, 且未增加額外硬件開銷, 比經典無線傳感器節點的整體定位性能更優.

1 無線傳感器網絡結構

圖1 無線傳感器網絡的基本結構Fig.1 Basic structure of wireless sensor networks

無線傳感器網絡常包含大量的節點, 節點采用隨機方式進行部署, 分布極不均勻, 單個節點的數據處理和存儲能力有限, 因此節點之間信息冗余較高, 這些節點自動構成一個無線網絡, 對監測對象信息進行采集, 通過與相鄰節點之間的信息轉發方式將信息發送到匯聚節點, 匯聚節點主要負責數據的融合, 然后將數據發送到移動通信網絡, 移動通信網絡將數據發送到需要的用戶. 在整個網絡中, 每個節點均有一個用于識別的號碼, 普通節點的能量通常有限, 且不能進行補充, 而匯聚節點的能量是無限的, 不受限制, 而且節點的位置固定不能移動, 其基本結構[14]如圖1所示.

2 DV-Hop算法和粒子群算法

2.1 DV-Hop算法

傳感器網絡有兩類節點, 其中一類節點獲得自己所在位置坐標的錨節點, 另一類節點不知道自己位置的節點, 只能通過錨節點估計其位置, 稱為未知節點. DV-Hop算法是一種根據路由的跳數實現未知節點定位的經典算法, 且節點定位的成本低, 自適應能力強, 步驟如下：

1) 傳感器節點之間的最小跳數計算. 每個錨節點在自己通信范圍內不斷廣播自己的位置信息, 收到信息的節點保留最小跳數, 同時對鄰居節點進行廣播, 這樣全部節點都會記錄與所有錨節點之間的最小跳數.

2) 計算無線傳感器網絡兩個錨節點之間的平均跳距. 根據錨節點的位置信息和最小跳數可得到任意兩個錨節點i和j之間的平均跳距, 計算公式為

(1)

式中:hi,j表示錨節點i和j之間的最小跳數； (xi,yi)和(xj,yj)分別表示錨節點i和j的位置坐標.

3) 未知節點位置的估計. 根據未知節點u和錨節點i之間的最小跳數tu,s及平均跳距可得到未知節點u和錨節點i之間的距離為

du,s=HopSize×tu,s.

(2)

4) 當未知節點得到附近3個錨節點的距離值時, 可采用三邊定位算法得到未知節點的位置. 設D為待定位傳感器節點,A,B,C為錨節點, 其位置分別為(xA,yA),(xB,yB),(xC,yC), 則可建立如下關系式：

(3)

式中: (x,y)表示D的位置坐標;dA,dB和dC表示節點D與錨節點A,B,C之間的距離.

三邊定位算法只利用3個節點的位置信息, 提供的信息有限, 因此可引入極大似然估計法對未知節點的坐標信息進行估計. 設共有n個錨節點, 節點D與其距離分別為di(i=1,2,…,n), 則可建立如下方程：

(4)

對式(4)進行變換和簡化后, 可得:

(5)

設

可建立線性方程Ax=b, 從而得

x=(ATA)-1ATb.

(6)

采用最小二乘法, 根據式(6)可得到未知節點D的位置坐標.

對DV-Hop算法的實現過程進行分析可知, 測距決定了無線傳感器網絡節點的定位精度, 通常情況下, 根據信號強度對測距進行估計. 設節點發射功率為Pt, 發射節點和接收節點之間的距離為d,λ表示發射波長, 則接收節點收到的信號功率為

(7)

式中:Gt和Gr分別表示發射節點和接收節點的增益;L表示功率損耗常數.

可將式(7)得到的信號功率轉換為傳感器節點之間的實際距離, 但在實際應用中, 由于受空氣、 樹木及建筑物等外界因素的影響, 根據信號強度得到測距值與實際距離值之間存在一定的偏差, 從而導致節點定位誤差, 因此本文引入粒子群算法對測距進行修正.

2.2 粒子群算法

設粒子i的位置向量和速度向量分別為Xi=(xi1,xi2,…,xiD)和Vi=(vi1,vi2,…,viD), 其當前的最優位置和粒子群的當前最優位置分別為Pi=(pi1,pi2,…,piD)和Pg=(pg1,pg2,…,pgD), 則第(k+1)時刻, 粒子i的速度和位置變化公式為

式中相關參數的意義見文獻[15]. 慣性權重ω的線性迭代表達式為

(10)

當前的最優位置及粒子群當前最優位置的更新公式分別為

(11)

f(Pg)=min{f(Pi)}.

(12)

標準粒子群算法也存在易出現局部最優解的缺陷, 因此本文引入混沌機制對粒子的位置進行擾動, 幫助其逃離局部最優解. Logistic混沌系統為

zi+1=μzi(1-zi),zi∈[0,1],μ∈(2,4].

(13)

選擇遺傳算法作為對比算法, 其對式(14),(15)的求解目標函數值變化曲線如圖2所示. 由圖2可見, 粒子群算法的收斂速度明顯快于遺傳算法, 目標函數值更理想, 對比結果說明了粒子群算法的優越性.

圖2 兩種算法對目標函數的求解曲線Fig.2 Solving curves of objective function by two algorithms

3 算法設計

3.1 誤差修正系數

為了降低測距誤差, 引入距離誤差修正系數μ對未知節點潛在的區域進行限制, 以提高無線傳感器網絡測距的準確性. 距離誤差修正系數μ的求解步驟如下:

1) 采用信號強度技術估計未知節點D與m個錨節點之間的距離di(i=1,2,…,m);

2) 隨機選擇3個錨節點作為參考節點, 得到D的位置約為(x′,y′)；

(16)

5) 將ei的平均值作為距離誤差修正系數：

(17)

6) 未知節點可行域范圍的約束條件為

(18)

3.2 節點定位數學模型

節點定位的數學模型可采用如下形式進行描述：

(19)

無線傳感器網絡節點定位的目標函數為

(20)

其中M表示距離誤差懲罰因子.

3.3 粒子群算法修正測距的無線傳感器節點定位步驟

1) 初始化粒子群算法的參數, 如慣性權重、 最大迭代次數;

2) 計算無線傳感器網絡節點定位的μ, 并確定目標函數;

3) 初始化粒子群的種群;

4) 根據目標函數計算每個粒子的適應度值, 并確定Pi和Pg;

5) 迭代次數增加, 更新慣性權重, 并更新每個粒子的位置和速度, 產生新一代的粒子群;

6) 計算新一代粒子群的適應度值, 并對Pi和Pg進行更新;

7) 如果當前迭代次數超過最大迭代次數, 則得到無線傳感器節點的位置.

粒子群算法修正測距的無線傳感器節點定位流程如圖3所示.

圖3 粒子群算法修正測距的無線傳感器節點定位流程Fig.3 Flow chart of ranging distance modified by particle swarm algorithm for wireless sensor nodes location

4 仿真測試

選擇DV-Hop算法、 遺傳算法修正測距的無線傳感器節點定位算法在相同實驗環境下進行仿真對比實驗. 采用VC++6.0進行編程實現定位算法. 定位結果采用如下定位誤差進行分析：

(21)

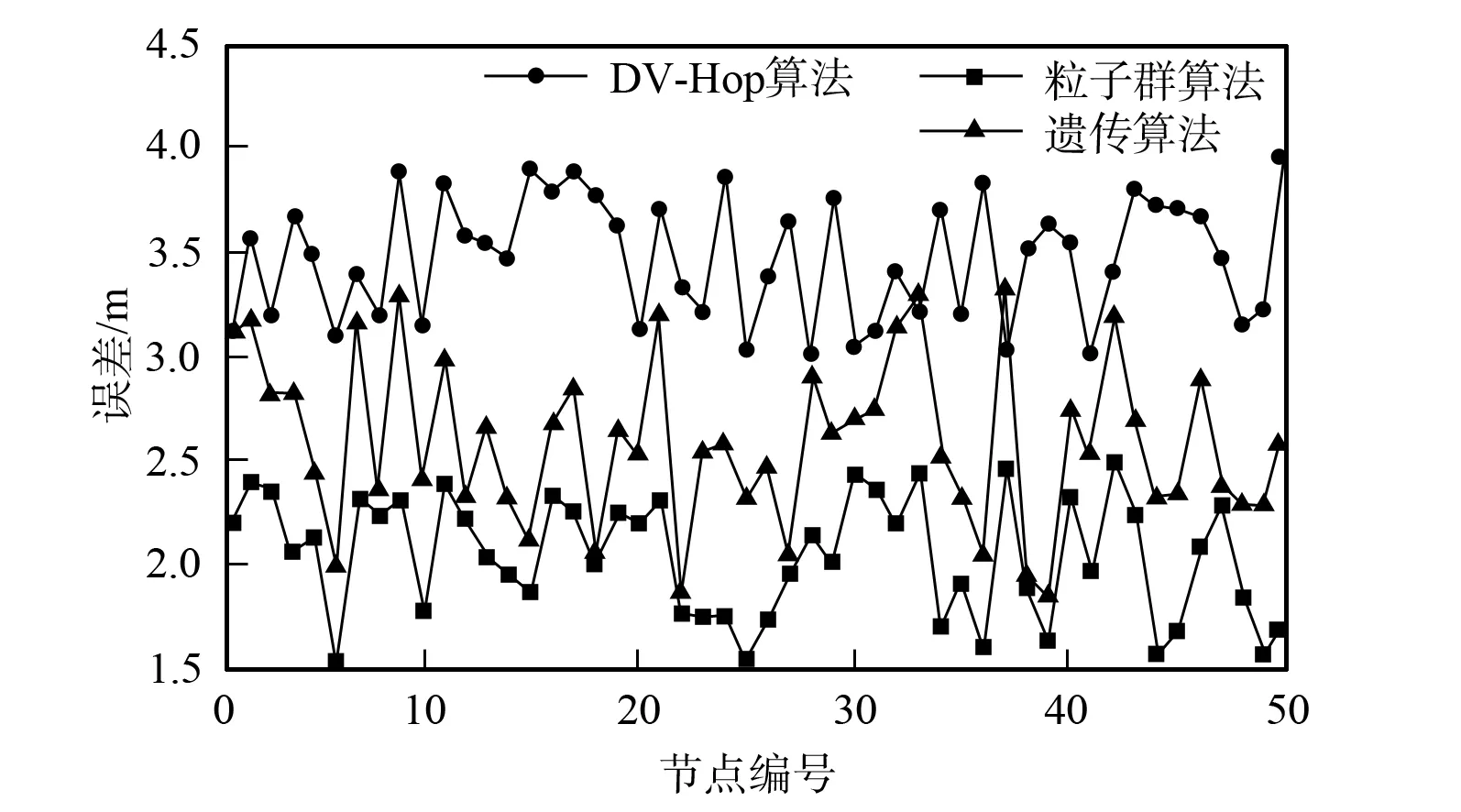
圖4 不同算法的傳感器節點定位誤差變化曲線Fig.4 Location error variation curves of sensor nodes for different algorithms

統計DV-Hop算法、 遺傳算法修正測距的無線傳感器節點定位算法和粒子群算法修正測距的無線傳感器節點定位算法的節點定位誤差(m), 結果如圖4所示. 由圖4可見, DV-Hop算法的節點定位誤差最大, 其次為遺傳算法, 而粒子群算法修正測距的無線傳感器節點定位效果最優.

為了分析不同算法的傳感器節點定位實際效果,圖5給出了DV-Hop算法(A)、 遺傳算法修正測距的無線傳感器節點定位算法(B)和粒子群算法修正測距的無線傳感器節點定位算法(C)的節點定位結果. 由圖5可見, 由于遺傳算法和粒子群算法對無線傳感器節點的測距誤差進行了校正, 因此無線傳感器節點定位效果優于傳統的DV-Hop算法, 同時粒子群算法定位效果優于遺傳算法, 這主要是粒子群算法克服了遺傳算法收斂速度慢、 易陷入局部最優的缺陷, 提高了無線傳感器節點定位精度.

圖5 不同算法的節點實際定位結果Fig.5 Actual location results of the nodes for different algorithms

綜上所述, 本文提出了一種粒子群修正跳距的傳感器節點定位算法, 仿真測試結果表明, 粒子群算法可解決當前DV-Hop算法定位過程存在的問題, 在不增加額外硬件的情況下, 有效改善了傳感器節點定位的效果, 具有一定的優越性.