基于重要度評估和IMPGA的航空保障裝備型譜規劃
王堅浩, 張 亮, 史 超, 車 飛
(空軍工程大學裝備管理與無人機工程學院, 陜西 西安 710051)
0 引 言
航空保障裝備是指配屬于部隊維修保障機構直接或間接用于飛行機務保障和飛機維修的各種工具、小型設備、地面保障設備、測試設備、修理工藝裝備等,是維持航空裝備作戰能力的重要物質基礎。近年來,隨著我國航空工業的穩步發展,航空保障裝備已經初步形成了通用化、綜合化、模塊化的發展系列,但與主戰航空裝備成體系發展與建設的需求相比,仍然存在很大差距,其主要原因是現有航空保障裝備采取基于型號的配套發展模式,強調與主裝備同步論證、同步配套,缺乏保障裝備體系論證和規劃,使得航空保障裝備種類繁雜、功能重復,技術體制不統一,通用化、系列化水平低,機動能力和多機種保障能力弱[1]。因此,有必要梳理已有航空保障裝備,規劃待研發裝備,通過優化整合,形成通用航空保障裝備系列型譜,實現航空保障裝備的系列化、規范化,以提升航空裝備保障效能,增強航空保障裝備型譜發展決策的科學性和有效性。
型譜規劃從產品型譜管理[2-6]概念延伸而來,型譜規劃不能簡單地理解為將現有的不同規格的同類產品簡單羅列,匯集成表格、圖冊或文書,而是具有一系列特定要求、經過優選的產品系列[7]。針對型譜規劃問題,較早開始研究型譜規劃的航天領域大多采用基于成熟度評估和優選的型譜規劃方法[8-10],但該方法缺乏定量的規劃模型和算法;在民用產品領域,文獻[11]基于優先數系提出了產品族型譜的交互系列和自動系列規劃模型,其中交互系列規劃適用于新產品設計,自動系列規劃適用于適應性設計;在保障裝備領域,文獻[12]建立了在完成保障任務前提下最小化保障裝備種類的保障裝備型譜整數規劃方法,但整數規劃方法屬于傳統的精確求解方法,其優化效率有待進一步提升。
基于以上分析,本文針對目前航空保障裝備種類繁雜、功能重復,技術體制不統一,通用化、系列化水平低以及傳統規劃方案論證中方案組合量大、評估體系復雜、綜合效率低等問題,提出了基于重要度評估和改進多種群遺傳算法(improved multi-population genetic algorithm,IMPGA)的航空保障裝備型譜規劃方法,首先建立型譜重要度評估指標體系,然后采用結合熵權和灰色群組聚類的組合賦權模型,最后基于IMPGA采用進化方式進行型譜優化方案求解,將型譜重要度綜合評估值與優化費用之比作為適應度函數,在多次迭代、反復對比中獲得型譜重要度評估值高和費用可控的最優方案。
1 基于熵權和灰色聚類的重要度評估
1.1 航空保障裝備型譜重要度評估指標體系
航空保障裝備型譜是指能滿足較長時期和一定范圍內全部使用要求的最少數目的航空保障裝備系列,是航空保障裝備系列化、通用化的頂層規劃,明確了航空維修保障裝備發展與應用方向,組成航空保障裝備型譜的每個個體在型譜體系中發揮不同的作用,使得不同保障裝備的重要程度存在區別。而型譜重要度是指保障裝備在型譜體系中的重要程度,作為保障裝備在型譜體系中的重要屬性,能夠定量地反映保障裝備對型譜體系的貢獻程度,在一定程度上也反映了保障裝備型譜優先級排序,屬于航空保障裝備型譜規劃與設計方案的初步篩選。根據航空保障裝備型譜規劃與設計過程,綜合考慮保障裝備研制主體、使用主體和功能、需求,建立如表1所示的航空保障裝備型譜重要度評估指標體系。
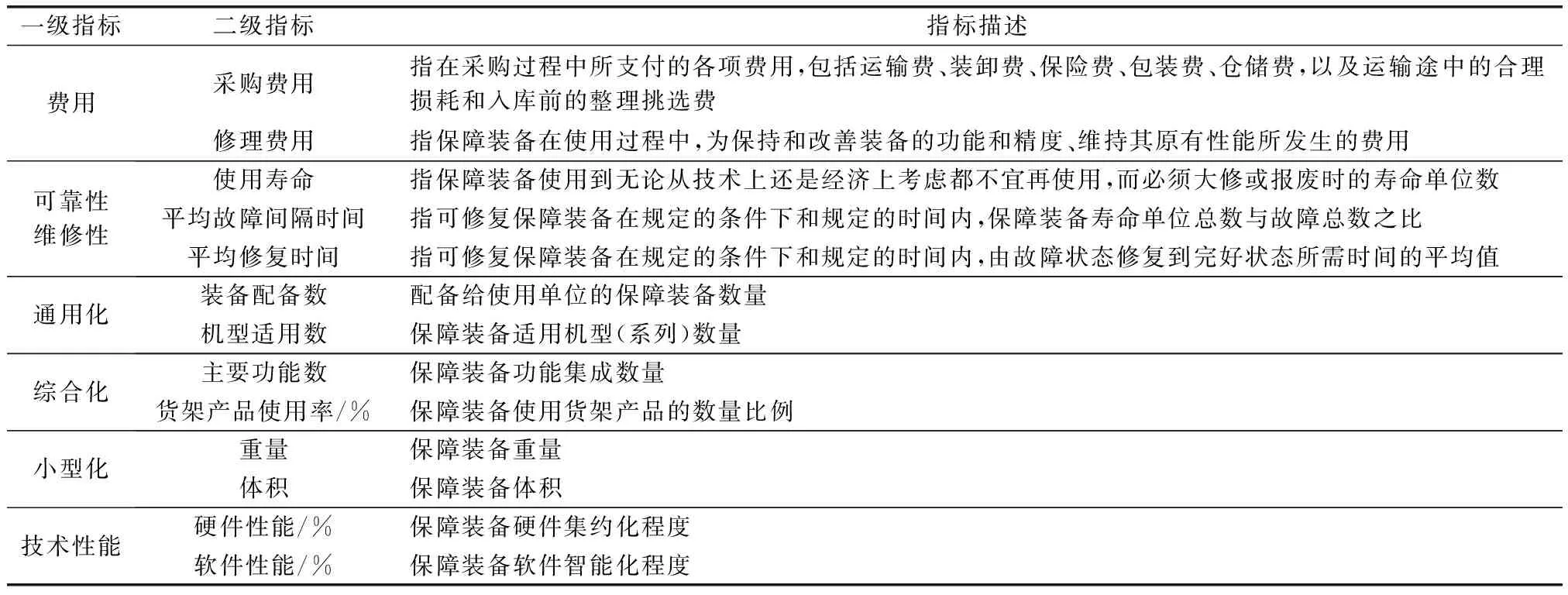
表1 航空保障裝備型譜重要度評估指標體系
1.2 基于熵權和灰色聚類的型譜評估指標賦權
評估指標賦權方法[13-18]主要包括主觀賦權法、客觀賦權法和組合賦權法,其中以組合賦權法應用最為廣泛。因此,本文采用結合熵權和灰色群組聚類的組合賦權方法來確定評估指標權重。
假設在預先給定的評估準則下,由m個來自相關領域的專家對這n個評估指標進行評價,得到評價判斷矩陣A,將矩陣A進行歸一化處理,可得評價指標的排序向量U=(u1,u2,…,un)T,其中
,i=1,2,…,n
(1)
(2)
根據專家群中每個專家給出的個人排序向量,可得專家群的排序矩陣為
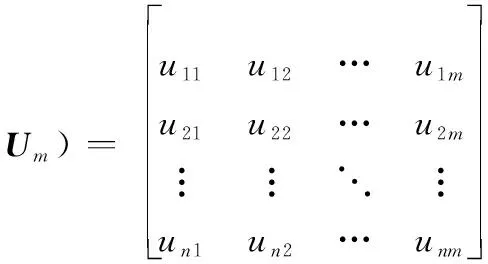
(3)
對于排序向量Ui與Uj,其相似程度可用灰色關聯度eij進行度量,則Ui、Uj(i≤j)的灰色關聯度為
(4)
式中,
(5)
(6)
則專家群灰色關聯度矩陣為
(7)
式中,取定閾值θ∈[0,1],當eij≥θ(i≠j)時,可認為Ui、Uj具有同類判斷性質,即認為專家i與j可聚為一類。閾值θ越接近1,分類就越細。
專家群中每位專家的權重由兩部分組成:一是類間權重,即通過兩兩之間的灰色關聯度,將意見相近的專家聚為同一類,該類的權重主要取決于類容量的大小。由于類容量較大,反映了較多專家的意見,其類間權重應較大;二是類內權重,即每位專家自身所在的類別中的權重,其權重大小取決于該專家的熵權。
假設有t類專家且專家k所在類中有φk(k≤m)個專家,則專家k所在類的類間權重λk為
,k=1,2,…,t
(8)
根據專家給出的個人排序向量可知,專家群中專家k的排序向量的信息熵為
(9)
專家k所在類的類內權重αk為
(10)
則專家k的總權重ηk為
ηk=λk·αk
(11)
則n個指標權重所組成的權重向量可表示為
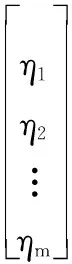
(12)
1.3 型譜評估信息集結
通過實地調研,收集航空保障裝備研制、生產等評估信息后,將指標信息與其對應的權重信息進行綜合集結,采用線性加權法對各級指標向上一級進行集結,即
(13)
式中,wi為一級指標權重;wij為二級指標權重;Cij為經歸一化和無量綱化處理后的評估信息值;TE為型譜重要度評估值。
2 基于IMPGA的型譜優化方案求解
2.1 航空保障裝備型譜優化方案求解模型
航空保障裝備型譜優化方案是在不涉及新研航空保障裝備的前提下,主要通過現有航空保障裝備的兼并、優選實現型譜綜合集成方案。所謂綜合集成是指在現有航空保障裝備型譜系列中選擇一種或幾種保障裝備進行改造升級,在滿足原有保障功能的同時,替換另一種或幾種保障裝備。在型譜優化方案求解過程中,既要保留型譜重要度評估值較高即型譜優先級較高的保障裝備,同時還要使綜合集成費用可控。因此,航空保障裝備型譜優化求解方案本質上是一類在航空保障裝備型譜重要度評估和費用約束的基礎上設計航空保障裝備型譜綜合集成方案問題。
對于由n個保障裝備構成的航空保障裝備集E={E1,E2,…,En},其中?Ei∈E,其屬性主要包括:型譜重要度評估值TE={TE1,TE2,…,TEn};保障裝備數量NE=[NE1,NE2,…,NEn];綜合集成費用CE=(CEij)n×n,其中CEii=0。
當航空保障裝備按照型譜優化方案求解進行綜合集成,其綜合集成型譜重要度評估值T和綜合集成費用C分別為
TΣ=sum (TE)-sum (ME-ETE)
(14)
CΣ=sum[(ME-E·CE)NE]
(15)
式中,·表示矩陣點乘;sum 表示向量元素求和。
航空保障裝備型譜優化求解考慮以綜合集成型譜重要度評估值與綜合集成費用之比最大化,因此型譜優化方案求解模型為
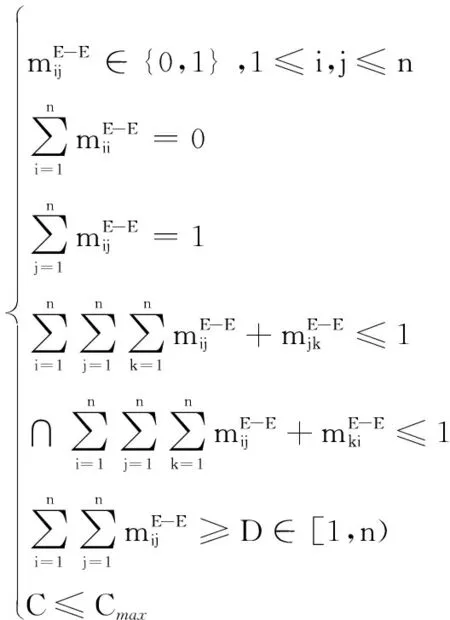
(16)
式中,約束1為決策變量取值約束;約束2、3和4為決策變量邏輯約束,約束2表示保障裝備Ei不能被自身集成,約束3表示保障裝備Ei和Ek不能同時集成Ej,約束4表示保障裝備Ei集成Ej和Ej集成Ek不能同時發生;約束5表示綜合集成數量約束;約束6表示綜合集成費用約束。
2.2 IMPGA算法求解
航空保障裝備型譜優化方案求解模型是一類典型的0-1背包問題,該問題屬于組合優化問題,包括多個約束條件,是數學中一種經典的NP完全問題。目前主要采用遺傳算法[19]、差分進化算法[20-21]、粒子群算法[22-24]、人工蜂群算法[25-26]和蝙蝠算法[27-28]等群體智能優化算法對背包問題進行求解,但均存在不同程度的早熟收斂問題。多種群遺傳算法(multi-population genetic algorithm,MPGA)[29-30]是在標準遺傳算法(standard genetic algorithm,SGA)[31]的基礎上,采用多種群并行進化的思想,不同種群賦予不同的交叉概率和變異概率,兼顧算法的全局搜索和局部搜索能力,各個種群之間通過移民算子進行信息交換,利用人工選擇算子選出各種群的最優個體放入精華種群加以保存。MPGA結構圖如圖1所示。
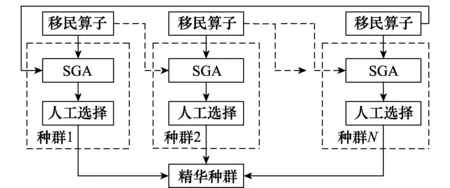
圖1 MPGA結構圖Fig.1 Structure chart of MPGA
本文針對航空保障裝備型譜優化方案求解問題提出了一種IMPGA優化算法,在基于MPGA優化算法的基礎上,IMPGA優化算法主要有以下3個方面的改進:①針對型譜優化方案求解模型中決策變量取值約束和邏輯約束,導致采用二進制染色體編碼方式會產生較多的不可行解問題,設計具有修復操作的染色體編碼以減小最優解搜索范圍,提高算法求解效率;②針對型譜優化方案求解模型中綜合集成數量約束和費用約束,結合適應度函數設計和懲罰函數約束處理方法,以提高算法收斂速度;③針對SGA優化算法中的固定常量型交叉和變異概率,在遺傳算子設計過程中采用控制參數自適應調整策略以平衡算法全局搜索和局部搜索能力。
下面從以上3個方面介紹IMPGA求解算法,并給出算法詳細流程。
(1) 具有修復操作的染色體編碼
M=reshape (x,n,n);
M=MT;
fori=1:n
forj=1:n
ifM(i,j)= =1
M(:,j)=0;M(i,:)=0;
fork=1:n
ifk~=i
M(k,j)=0
end if
end for
end if
end for
end for
其中,M=reshape (x,n,n)為將染色體x轉換為矩陣M。
(2) 適應度函數設計和約束處理
適應度函數的構造對優化算法的收斂性能和最優解質量影響較大,通常情況下適應度函數通過目標函數轉化而成;此外,按上述染色體編碼方式,雖然解決了決策變量邏輯約束問題,但仍然會產生一些不可行的型譜優化方案,即不滿足綜合集成數量約束和費用約束,因此在計算各個染色體的適應度函數值之前,需要對其是否滿足綜合集成數量約束和費用約束的型譜優化方案進行判斷,當不滿足綜合集成數量約束和費用約束,則通過相應的懲罰函數對其進行懲罰。因此,本文采用將不滿足綜合集成數量約束和費用約束的不可行染色體適應度函數值直接置0的方法。因此,將適應度函數設計為
(17)
(3) 遺傳算子設計
遺傳算子主要包括選擇算子、交叉算子和變異算子,本文分別采用隨機遍歷抽樣方法進行選擇操作,單點交叉方法進行交叉操作和均勻變異方法進行變異操作;此外,設計自適應交叉和變異概率,根據進化過程中父代種群適應度函數值的自動調整,具體表達式為
(19)
式中,Pcinitial和Pminitial分別為初始交叉和變異概率;Pcmin和Pmmin分別為最小交叉和變異概率;favg為種群平均適應度函數值;fmax為種群最大適應度函數值。
IMPGA算法流程如下:
步驟1根據航空保障裝備數量n,設置種群規模NIND和種群數MP ,采用上述染色體編碼方式,隨機產生初始種群Chrom ,并采用強制修正機制對染色體進行修復操作;
步驟2計算本文設計的適應度函數值;
步驟3根據適應度函數值進行移民操作和人工選擇操作,將各種群最優個體放入精華種群EliteChrom ;
步驟4將精華種群EliteChrom 作為算法終止的判斷依據,采用最優個體最少保持代數作為終止判據,即當最優個體保持代數超過所設置的值時,判斷算法收斂,否則轉步驟5;
步驟5采用本文設計的選擇算子、交叉算子和變異算子進行各項遺傳操作,生成下一代種群,并返回步驟2。
3 實例驗證與分析
以某類航空保障裝備型譜規劃為例,該類航空保障裝備目前總共有8個型號,各型號間技術狀態參差不齊,產品標準化程度低等問題,給航空裝備使用、維護、保障以及設備管理帶來很大不便,影響了裝備效能的充分發揮,亟待通過型譜規劃制定該類航空保障裝備型譜優化方案。
采用基于熵權和灰色群組聚類相結合的組合賦權方法進行賦權分析,根據重要度評估工作要求,邀請6位航空裝備發展論證與保障領域的專家組成專家決策群,按照一定的評估原則,采用層次分析法的九標度準則,對該類航空保障裝備型譜重要度評估指標體系中的費用、可靠性維修性、通用化、綜合化、小型化、技術性能這6個一級指標權重進行評價打分。由專家群的個人排序向量所構成的矩陣為
R=
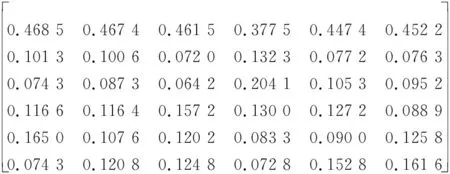
各專家之間的灰色關聯度矩陣為
E=

由E可知,經試探性取值,取閾值θ=0.99時,專家聚類結果較為合理,此時專家聚類結果為{(1,2,3,5),(4),(6)};則類間權重為λ1=16/18,λ2=1/18,λ3=1/18;專家群組熵向量為H=(0.107 8,0.142 5,0.144 9,0.106 5,0.160 2,0.164 4);根據熵權理論,對于第1類專家,可得其類內權重分別為α11=0.259 0,α12=0.248 9,α13=0.248 2,α15=0.243 8;對于第2、3類專家,由于其自成一類,則類內權重為α24=α36=1。
由此可得一級指標的權重向量為W=(0.456 2,0.089 8,0.090 0,0.127 0,0.119 4,0.117 6)。
同理,可求得二級指標權重,根據所收集到的相關評估信息,經歸一化和無量綱化,各級評估信息集結為最終的重要度綜合評估值如表2所示。
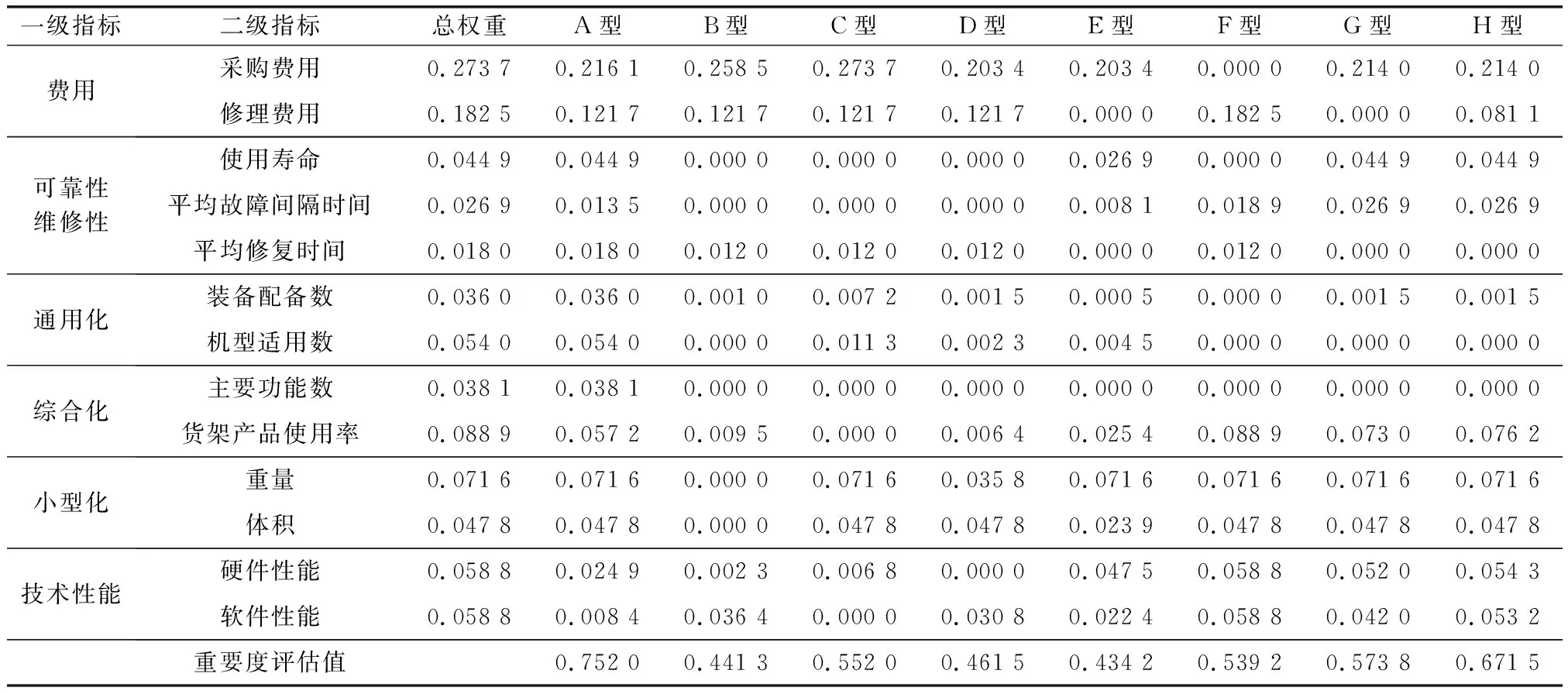
表2 航空保障裝備型譜重要度評估信息集結
該類航空保障裝備中各型保障裝備數量NE=[71,3,15,4,2,1,4,4],保障裝備集成數量D=5,集成費用約束Cmax=500,集成費用矩陣為
C=
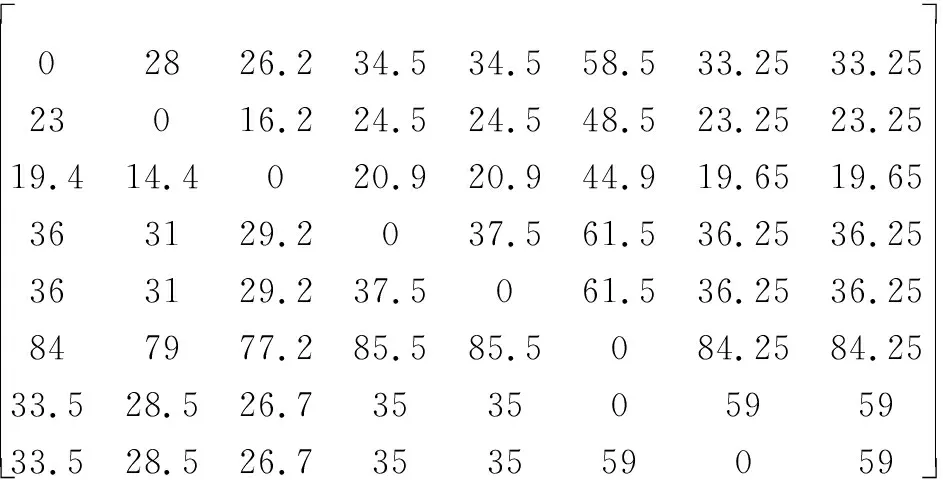
IMPGA參數設置如下:種群規模NIND= 40、種群數目MP=10、初始交叉和變異概率Pcinitial和Pminitial分別在區間[0.7,0.9]和[0.001,0.05]隨機選取、最優個體保持代數為10,利用IMPGA進行該類航空保障裝備型譜規劃,規劃方案即優化方案矩陣為
由優化方案矩陣ME-E可知該類8型航空保障裝備型譜規劃方案為:A型保障裝備升級集成B、D和G三型保障裝備;C型保障裝備升級集成E和F兩型保障裝備;保留H型保障裝備。
該類8型航空保障裝備型譜規劃方案下的最優解為9.2534E-03,綜合集成費用為441.7,最優解變化過程如圖2所示。
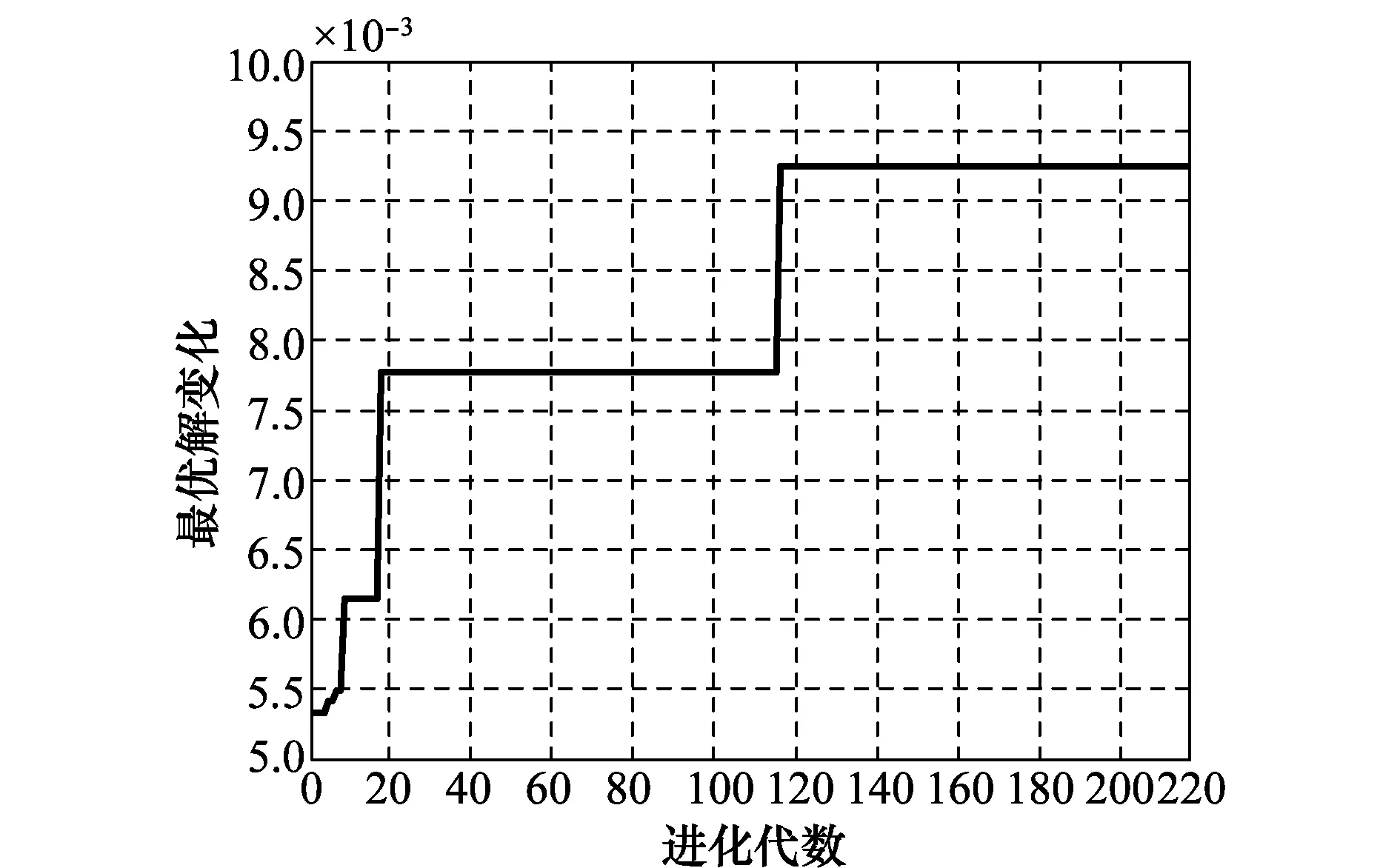
圖2 最優解變化過程Fig.2 Changing process of optimum solution
4 結 論
針對目前航空保障裝備種類繁雜、功能重復,技術體制不統一,通用化、系列化水平低及傳統規劃方案論證中方案組合量大、評估體系復雜、綜合效率低等問題,提出基于重要度評估和IMPGA的航空保障裝備型譜規劃方法,并通過某類8型航空保障裝備型譜規劃實例驗證了方法的有效性。本文所提方法從縱向層面(單一類型)對航空保障裝備型譜規劃進行研究,在此基礎上研究相應的橫向層面(全類型)的航空保障裝備型譜規劃方法將是下一步工作重點,這就需要重新考慮評估指標體系選擇、評估信息收集分析、優化算法選擇和參數設置等問題,此外將費用可控的單目標優化擴展到費用和風險可控的多目標優化也將是下一步的研究重點。

