特征匹配驅動的IVIFSs相似性測度模型研究
江文奇, 祁晨晨
(1. 南京理工大學經濟管理學院, 江蘇 南京 210094; 2. 江蘇產業集群決策咨詢研究基地, 江蘇 南京 210094)
0 引 言
直覺模糊型多準則決策問題是近年來多準則決策研究領域的熱點問題之一。傳統的直覺模糊集(intuitionistic fuzzy sets, IFSs)采用隸屬度、非隸屬度和猶豫度表征評估值,但是忽視了決策信息的模糊性和決策者認知的局限性[1]。區間直覺模糊集(interval-valued intuitionistic fuzzy sets,IVIFSs),使用區間值來表示隸屬度、非隸屬度和猶豫度,增強了表達信息的不確定性能力,可以有效處理數據的不確定性和模糊性[2]。
IFSs相似性測度是直覺模糊型多準則決策的重要環節,在模式識別等領域得到廣泛應用[3]。文獻[4-5]最先提出了IFSs相似性測度距離模型,文獻[6]分析了這兩個模型的缺點并進行了改進。2002年,李登峰等提出了IFSs的相似性測度模型,被國際學者命名為登峰-春田相似性測度,為相似度設計奠定了研究基礎[7-8]。文獻[9]基于直接算子重新定義了相似性測度。文獻[10]則根據反直覺的案例重新定義了相似性測度模型。文獻[11]運用幾何距離模型重新定義了連續距離和相似性測度。文獻[12]拓展了基數測度,設計了基于t范數的相似性測度。文獻[13]則基于Hausdorff距離計算IFSs間的距離進而提出新的相似性測度模型。文獻[14]指出一些相似性測度并不有效,提出了幾種新的測度模型。文獻[15]運用歐式距離進行相似性度量;文獻[16]將IFSs轉化為直角三角形,基于重心提出相似性度量模型。
IVIFSs相似性測度分成兩類,第一類設計借鑒IFSs相似性測度思想。文獻[17]分別利用區間數中點值和Hausdorff距離定義相似性測度。文獻[18]結合IFSs的Hamming距離和補集提出了IVIFSs相似性測度。文獻[19]設計包含猶豫度的IVIFSs歐氏距離公式。文獻[20]分別將文獻[11]中IFSs相似度拓展至IVIFSs相似性測度中。
另一種類型是設計全新的相似性測度模型。文獻[21-23]構建了IVIFSs的熵和相似性測度的關聯性,進而設計了基于熵的相似性測度。文獻[24]采用shapely函數定義了幾個賦權的shapely相似性測度模型。文獻[25]對IVIFSs進行約簡,進而提出了Dice相似性測度。文獻[26]考慮了猶豫度因素并運用相關系數表示相似度。文獻[27]考慮了猶豫度對隸屬度和非隸屬度的影響,結合TOPSIS構建相似性模型。文獻[28]考慮隸屬度、非隸屬度和區間中點的影響并定義了新的相似度。文獻[29]分別考慮隸屬度與非隸屬度的距離,提出了新的相似性模型。
總體上看,IFSs的相似性測度主要以距離測度為主,采用左右端點分別比較的方式確定任意兩個IFSs的隸屬關系[30]。在含有IVIFSs的決策環境下,難以采用IFSs左右端點進行直接比較,因此提高了相似性測度特征匹配的難度。同時,IVIFSs相似性測度大部分考慮區間端點和中點值,容易造成信息損失,導致相似度測度模型可能不滿足相似度性質,存在著反直覺現象,且部分IVIFSs相似性區分度不高,難以展現決策方案的差異性。于是,基于IVIFSs的特點,本文首先提出其相似性解釋框架,分析現有IVIFSs相似性測度與解釋框架匹配性難度,通過轉換IVIFSs進而提出了一種新的IVIFSs相似性測度模型,并說明其科學性和應用價值。
1 IVIFSs相似性測度性質
定義1[1]設X是一給定論域,IFSA={〈x,μA(x),vA(x)〉|x∈X}。其中μA(x)和vA(x)分別為X中元素x屬于A的隸屬度和非隸屬度。μA:X→[0,1],vA:X→[0,1],且滿足條件0≤μA(x)+vA(x)≤1,x∈X。稱πA(x)=1-μA(x)-vA(x)為X中x屬于A的猶豫度。

定義3[7]如果映射S:IVIFS(X)×IVIFS(X) →[0,1],稱S(A,B)為IFSA∈IVIFS(X)和B∈IVIFS(X)間的相似度,且滿足5個特征條件:
① 0≤S(A,B)≤1;
②S(A,B)=1當且僅當A=B;
③S(A,B)=S(B,A);
④S(A,B)=0當且僅當A=〈[0,0],[1,1]〉,B=〈[1,1],[0,0]〉或A=〈[1,1],[0,0]〉,B=〈[0,0],[1,1]〉;
⑤ 如果A?B?C,則S(A,C)≤S(A,B),S(A,C)≤S(B,C)。
⑥SA≤SB≤SC。
⑦ 如果SA=SB=SC,則HA≤HB≤HC。
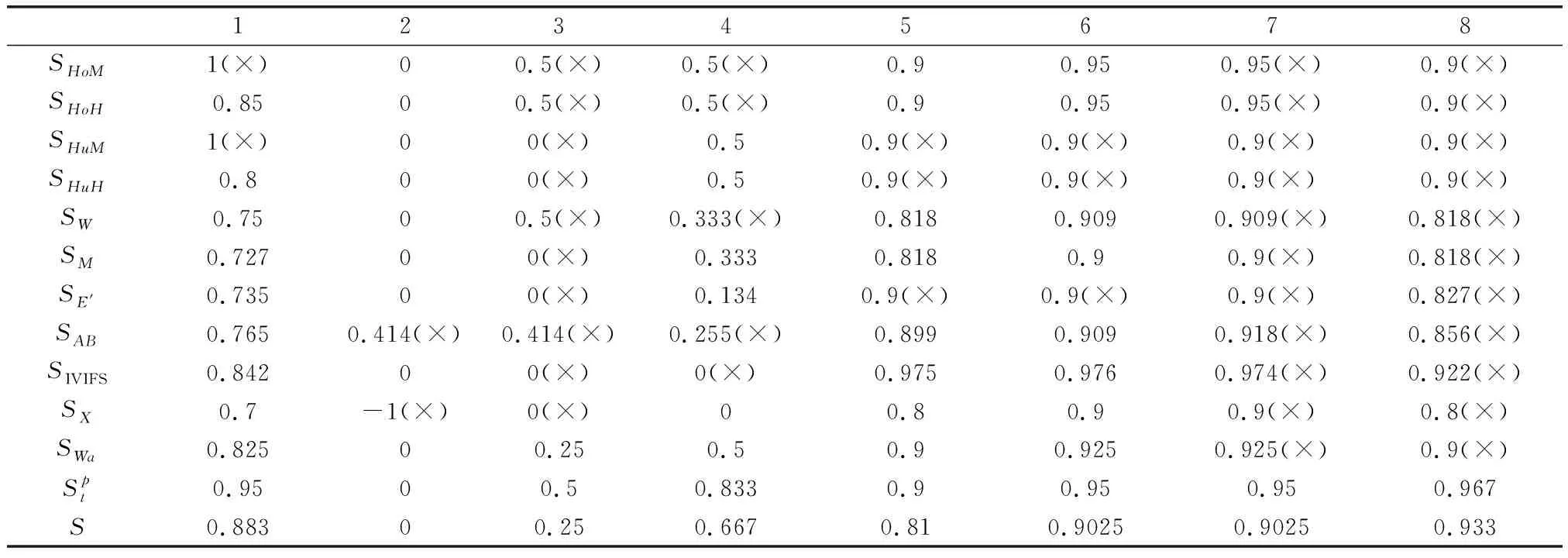
假設A=〈[0.3,0.5],[0.1,0.3]〉,B=〈[0.4,0.6],[0.2,0.4]〉,C=〈[0.4,0.6],[0.1,0.3]〉,采用區間數中點表示隸屬度和非隸屬度,A,B,C支持比率分別為0.667、0.625、0.714,故A和B相似度高于A和C,不滿足條件⑤中A?B?C,采用條件⑥有SA=0.1,SB=0.2,SC=0.3,即S(A,C) (1) 基于Hamming距離的相似度為 (1) (2) 基于歐氏距離的相似度為 (2) (3) 基于Hausdorff距離與Hamming距離的相似度為 (3) (4) 基于Hausdorff與歐氏距離的相似度為 (4) (5) 分別利用區間數中點值和Hausdorff測度等相似性測度方法[17],得到 (5) (6) (7) (8) (6) 基于熵測度的相似度[22]為 (9) (7) Meng[24]改進了Wei的相似度,提出SM為 (10) (8) 在歐式距離中考慮猶豫度,有相似度[19]為 (11) (9) 結合TOPSIS的思想構建的相似度模型為 (12) 式中 (10) 用相關系數表示相似度,即 (13) 式中 CIVIFS(A,B)= EIVIFS(A)= EIVIFS(B)= (11)相似度為 (14) (12) 結合歐氏距離和Hausdorff距離的相似度為 (15) (13) Dügenci[20]拓展了文獻[16]的相似度為 (16) (1)SH,SE,SHH,SHE只考慮了4個參數絕對值或平方,若他們相等則相似度相同,因此均不滿足條件⑥。如當A=〈[0.25,0.35],[0.25,0.35]〉,B=〈[0.35,0.45],[0.35,0.45]〉,C=〈[0.25,0.35],[0.35,0.45]〉,D=〈[0.35,0.45],[0.25,0.35]〉時SH(A,B)=SH(C,D)=0.9,SE(A,B)=SE(C,D)=0.9;SHH(A,B)=SHH(C,D)=0.975,SHE(A,B)=SHE(C,D)=0.95,然而根據記分函數有C (2)SHH和SHE不滿足條件④。當A=〈[1,1],[0,0]〉,B=〈[0,0],[1,1]〉時,SHH(A,B)=0.75,SHE(A,B)=0.5, 而A和B表示全部支持和全部反對,即S(A,B)=0,故SHH和SHE不合理。 (3)SHoM和SHuM違反了條件②、條件④和條件⑤。使用區間中點替代整個區間,會丟失原區間信息。如當A=〈[0.2,0.6],[0.2,0.4]〉,B=〈[0.4,0.4],[0.3,0.3]〉時,SHoM(A,B)=SHuM(A,B)=1,而A≠B;當A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉時,SHuM(A,B)=SHuH(A,B)=0,兩者相似度為0并不合理;當A=〈[0.2,0.3],[0.4,0.6]〉,B=〈[0.3,0.4],[0.4,0.6]〉,C=〈[0.3,0.4],[0.3,0.5]〉,根據條件⑤有A?B?C,然而SHuM(A,B)=SHuM(A,C)=SHuH(A,B)=SHuH(A,C)=0.9。 (4)SHoM,SHoH,SHuM,SHuH違反條件⑥。如A=〈[0.35,0.45],[0.15,0.25]〉,B=〈[0.45,0.55],[0.25,0.35]〉,C=〈[0.45,0.55],[0.15,0.25]〉,由記分函數可得A (5)SW違反條件⑥。熵到相似度轉換過程中使用的函數在某些情況下非區間直覺模糊數,反例同(4)。 (6)SM不滿足條件④和條件⑥。改進后的相似度可以保證轉換中的函數為IVIFSs,但當A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉時,SM(A,B)=0;其次不滿足性質條件⑥,反例同(4)。 (7)SE′違反了條件④:當A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉時,SE′(A,B)=0;此外不滿足性質條件⑤和條件⑥,反例同(3)與(4)。 (8)SAB違反了條件④:當A=〈[0,0],[1,1]〉,B=〈[1,1],[0,0]〉時,SAB(A,B)=0.414≠0;也同樣違反了條件⑥,反例同(4)。 (9)SIVIFS違反條件④。考慮猶豫度,克服距離測度造成的信息混淆。但當A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉時,SIVIFS(A,B)=0;違反了條件⑥,反例同(4)。 (10)SX違反條件①和條件④:A=〈[1,1],[0,0]〉,B=〈[0,0],[0,0]〉時,SX(A,B)=-1;違反條件⑥,反例同(4)。 (11)SWa滿足前5條性質,但違背條件⑥,反例同(4)。 如用“√”表示滿足該性質,“×”表示不滿足該性質,則上述分析結果可以總結如表1所示。 表1 現有文獻滿足約束條件情況 現有的IVIFSs相似性測度沒有充分考慮式(5)中IVIFSs的隸屬關系的局限性,故未能完全滿足相似度性質。盡管從記分函數角度出發來刻畫式(5),但仍然無法滿足其特征要求,有必要重新設計一個新的相似度函數。借鑒文獻[16]將IFS轉換為三角模糊數而獲取相似度的研究思路,本文考慮了IVIFSs端點不一致情形,將其轉化為三角模糊數而設計相似度測度,具體設計如下。 令 則轉化后的區間三角模糊數為 定義4A與B的相似度為 S(A,B)=[1-d(A,B)]×(1-|xA-xB|) (17) 式中 d(A,B)= (18) 重心分別為 /4 于是,證明定義4滿足上述7個性質。 (3)S(A,B)=S(B,A)顯然成立。 由以上可得S(A,C)≤S(A,B)。同理可得S(A,C)≤S(B,C)。 (6) 由SA≤SB≤SC,得 ≤0 6S(A,B)= {1-(SB-SA)/2}= {6-[2(HB-HA)+SB-SA]}×{1-(SB-SA)/2}= 6-4(SB-SA)- 2(HB-HA)+(HB-HA)(SB-SA)+(SB-SA)2/2 則 6(S(A,B)-S(A,C))= (SC-SB)[8-(SB+SC-2SA)]/2+[HB(SB-SA)+ HA(SC-SB)-HC(SC-SA)+2(HC-HB)] 其中 HB(SB-SA)+HA(SC-SB)- HC(SC-SA)+2(HC-HB)= (HB-HC)(SB-SA-2)+ HC(SB-SC)+HA(SC-SB)≥ (HA-HC)(SB-SA-2)+ (SC-SB)(HA-HC)= (HA-HC)(SC-SA-2) 得 12(S(A,B)-S(A,C))≥ (SC-SB)[8-(SB+SC-2SA)]+ 2(HA-HC)(SC-SA-2) 因為-4≤SB+SC-2SA≤4,得8-(SB+SC-2SA)≥0,即有:(SC-SB)[8-(SB+SC-2SA)]≥0。又HA-HC≤0,0≤SC-SA≤2,所以:(HA-HC)(SC-SA-2)≥0。因此有S(A,B)-S(A,C)≥0,即S(A,C)≤S(A,B)。 同理,S(A,C)≤S(B,C)。如果SA≤SB≤SC,如果為其他兩種情形,也可以證明S(A,C)≤S(A,B),S(A,C)≤S(B,C)。 證畢 6S(A,B)= 6[1-(SA-SB)/2]2 則 S(A,B)-S(B,C)= [1-(SA-SB)/2]2-[1-(SB-SC)/2]2= [(SA-SB)2-(SB-SC)2]/4-(SA-2SB+SC)= (SA-2SB+SC)[(SA-SC)/4-1] 針對文獻[31]的相似性測度式(16),當t=2,p=1時, (A,B)=12- 12-6(SA-SB) D1=|S(A,B)-S(B,C)|= |(SA-2SB+SC)|×(1-(SA-SC)/4) 因為-1≤SA≤1,-1≤SC≤1,有-2≤SA-SC≤2,0.5≤1-(SA-SC)/4≤1.5,因此D1≥D2,相比文獻[31],本文的相似性測度具有較強的區分度和辨別能力。 接著本文擬從實證角度進行分析。將本文的方法與16種相似度測度進行比較,具體見表2。其中p=1,t=2,數字后有(×)表示不滿足。 表2 區間直覺模糊數之間的各種相似度量方法比較 續表2 IVIFSs中的相互包含關系在現實中出現概率較低,導致其相似性測度模型很難與這種包含關系完全匹配。為了有效分析IVIFSs的隸屬關系對相似性測度設計的影響,本文采用記分函數和精確函數來加以刻畫,提出了新的IVIFSs的相似性測度性質解釋框架,接著分析對比了現有相似性測度的缺陷,以本文構建的性質框架為切入點,將IVIFSs轉換為區間三角模糊數,結合三角模糊數的距離和重心定義一個新的相似性測度函數,并通過理論證明驗證本文提出的相似性測度不僅可以滿足現有的和改進的相似性測度性質,而且比現有的相似性測度有更高的區分度。2 現有IVIFSs相似性測度分析
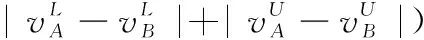
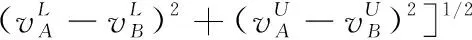
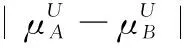

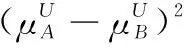
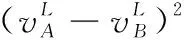

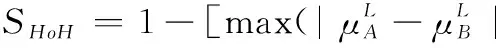

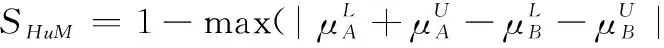

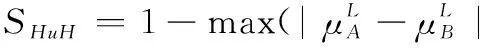

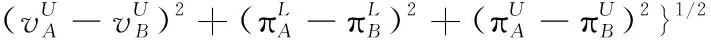
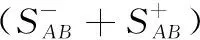
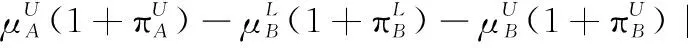
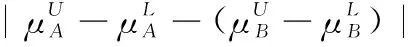
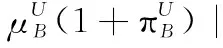

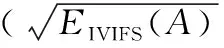
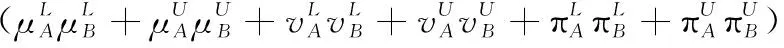

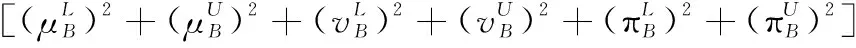
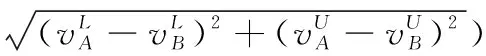
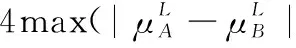

3 現有IVIFSs相似性測度性質分析


4 新的IVIFSs相似性測度設計
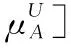
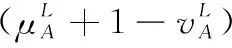
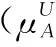


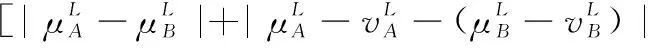

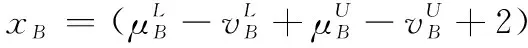
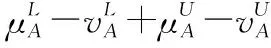
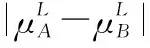
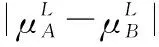
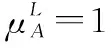

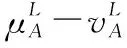

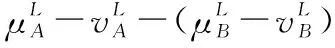
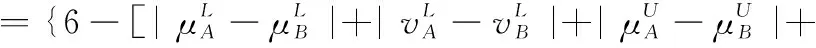
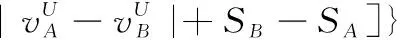
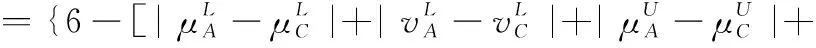
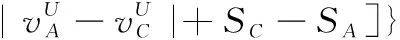
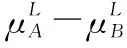
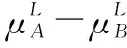
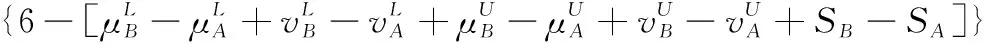
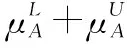
5 新的IVIFSs相似性分析與驗證
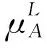
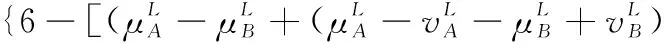
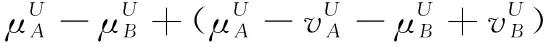
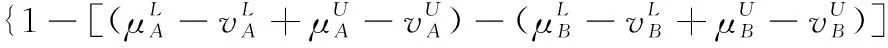
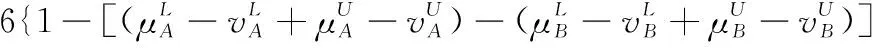
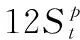
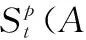
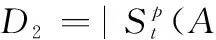

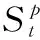
6 結 論

