鋼中非金屬夾雜物對時頻域超聲參量的影響

肖會芳，陳丹，徐金梧

?

鋼中非金屬夾雜物對時頻域超聲參量的影響

肖會芳1，陳丹2，徐金梧2

(1. 北京科技大學 機械工程學院，北京，100083； 2. 北京科技大學 鋼鐵共性技術協同創新中心，北京，100083)

通過建立包含夾雜物的二維金屬板超聲測量數值分析模型，研究超聲信號隨夾雜物的深度、厚度和類型等屬性特征的變化規律，并通過超聲顯微鏡和掃描電鏡實驗驗證模型的有效性。研究結果表明：縱波聲速隨夾雜物厚度的增加呈線性遞增，含有Al2O3夾雜物的聲速最大且增速最快，含有MnS夾雜物的聲速最小且增速最慢，縱波聲速可以作為判定內部是否存在夾雜物的參量；不同超聲參量隨入射波長的變化關系曲線，可用于判定夾雜物的厚度；當夾雜物深度位于鋼板厚度的中間時，衰減系數最大，且含有MnS夾雜物引起的聲波幅值衰減最嚴重，含有TiN夾雜物的聲波幅值衰減最小。

非金屬夾雜物；超聲參量；數值仿真；多值域；影響特性

鋼中非金屬夾雜物的存在破壞了材料的連續性，嚴重影響鋼的加工性能，降低了鋼的承載能力和疲勞壽命。對鋼中夾雜物特征包括位置、尺寸、類型等的準確檢測不僅能夠反映鋼的冶煉工藝，而且能為夾雜物的有效控制提供基礎[1?7]。超聲無損檢測方法由于對樣品沒有破壞性，能夠實現夾雜物的空間定位，同時能有效避免大型夾雜物的漏檢，目前已被廣泛應用于材料內部缺陷的檢測[8?12]。要實現鋼內部夾雜物的超聲檢測，最關鍵的問題是如何通過測量獲得的回波信號或超聲掃描圖像辨識夾雜物的屬性特征。但是，直接的超聲回波信號只能較為準確地判斷材料內部缺陷位置信息，而對夾雜物的類型難以確定，因而，明確夾雜物的類型、尺寸和深度等屬性特征對超聲測量信號的影響規律，對超聲方法檢測材料內部夾雜物具有重要的理論與實際意義。本文作者通過建立包含夾雜物的二維金屬板超聲測量模型，采用有限元數值計算的方法，對具有不同深度、不同厚度、不同類型夾雜物的材料內部超聲波場進行計算，獲得不同深度、不同厚度、不同類型夾雜物的回波信號，并分別計算其缺陷回波信號和底面回波信號的4個時域特征參量和2個頻域特征參量，獲得不同類型夾雜物的多值域超聲參量隨夾雜物厚度和深度的變化規律，并進行實驗驗證，為非金屬夾雜物的超聲檢測提供參考。

1 含夾雜物的二維金屬板模型

1.1 模型描述

研究內部夾雜物對超聲參量影響規律的二維金屬板超聲測量模型示意圖，如圖1所示。超聲檢測采用水浸縱波脈沖回波法，即采用水作為耦合介質傳遞超聲波，且僅有1個換能器同時激發和接收超聲波信號。二維矩形金屬板的厚度為，厚度為、深度為的夾雜物位于金屬板內部。壓電晶片半徑為，幾何焦距為的聚焦換能器產生的超聲波垂直入射，經過耦合介質水傳播至材料內部，并在水?鋼界面發生折射在材料內部二次聚焦，聚焦深度為。通過調整水程厚度w，保證換能器在材料內部的焦點位于夾雜物上表面，以獲得最大的橫向分辨率和聲壓強度，即=。

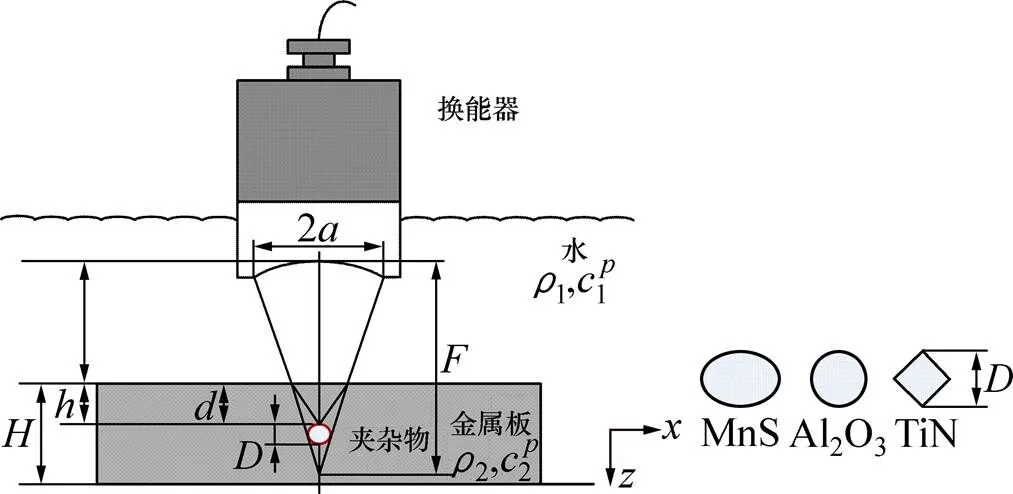
圖1 含夾雜物的二維金屬板超聲測量模型示意圖

由于夾雜物的存在改變了金屬板內超聲波的傳播特性，引起了缺陷反射回波和底面發射回波超聲特征參量的變化，因而，回波的超聲參量反映了夾雜物的特性信息。本文選取3種典型的夾雜物即塑性夾雜物MnS、脆性夾雜物Al2O3和高硬度夾雜物TiN進行分析。由于軋制過程中不同類型夾雜物的變形程度和形狀不同，塑性夾雜物經軋制后通常為扁平的條狀或片狀、脆性夾雜物經軋制后一般為球狀或鏈狀、而高硬度夾雜物在軋制前后的形狀不變，通常為立方體，因此，假設3種典型夾雜物的形狀分別為橢圓形、球形和菱形[13]。不同類型夾雜物的材料參數和聲參數如表1所示。對3種類型的夾雜物分別建立包含不同厚度和不同深度夾雜物的二維金屬板超聲測量模型，采用有限元方法，計算獲得金屬板上表面的反射回波曲線，并分別對缺陷回波和底面回波進行超聲特征參量提取，獲得超聲特征參量隨夾雜物厚度和深度的變化規律。計算中，鋼板的厚度=1.5 mm。

表1 不同介質的材料參數與聲參數

采用多物理場仿真軟件COMSOL求解超聲波場，并計算獲得回波曲線。換能器的激勵載荷是中心頻率c=50 MHz，時間Δ=60 ns的壓力載荷，如圖2所示。其在鋼中的縱波波長=0.12 mm。網格尺寸為/60，時間步長為0.2 ns。金屬板的左右設置吸收邊界，以消除計算模型寬度有限引入的邊界反射效應對內部超聲波場的影響[14?15]。計算時間=1.9 μs，保證金屬板上表面的回波信號中能夠包含二次底面回波。

1.2 有限元計算方法有效性驗證

采用有限元方法計算無夾雜物缺陷時的金屬板內部聲場分布，并與理論模型的計算結果進行對比，驗證本文有限元模型的準確性。仿真計算獲得的中心頻率為50 MHz換能器在水?鋼兩相介質中的瞬態聲場分布，如圖3(a)所示。從圖3(a)可知：在鋼中傳播的聲波在焦點位置(=0.75 mm)處匯聚，而被水?鋼界面反射的聲波以近似平面波的方式反向傳播。提取焦平面處的徑向聲壓分布，并與多元高斯聲束模型(MGB)計算的徑向聲壓分布對比，結果如圖3(b)所示。其中，多元高斯聲束模型的徑向聲壓分布表達式為[16?17]

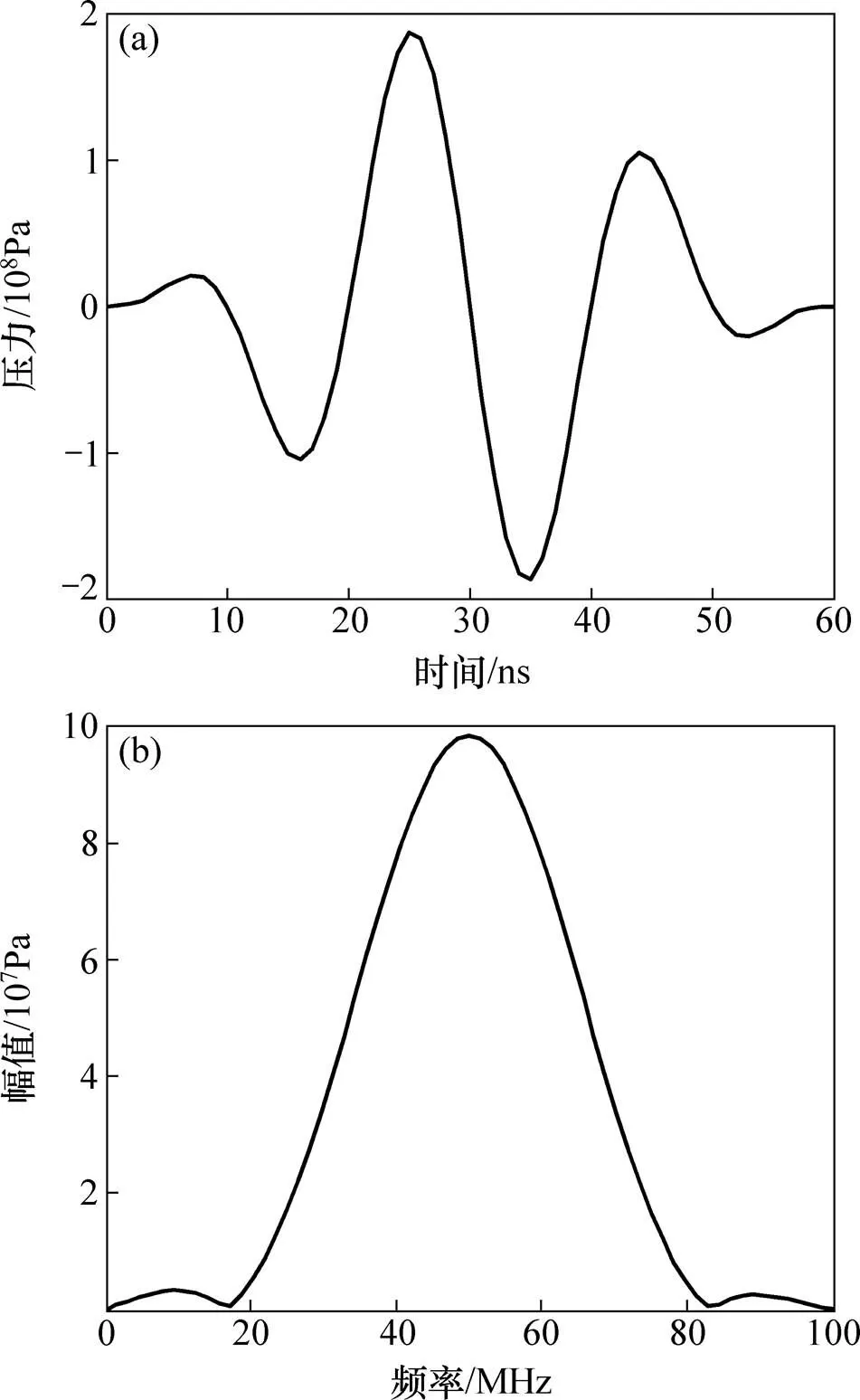
(a) 時域；(b) 頻域

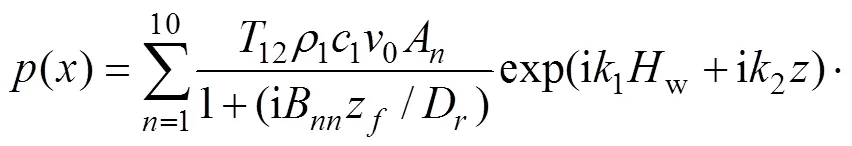
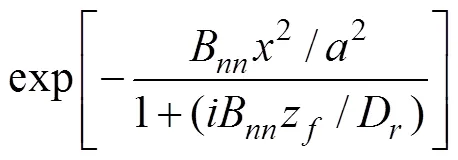
式中：12為水?鋼界面的透射系數，12=2/[1+(1/2)(1/2p)]，1為水的密度，1為水中聲速，2為鋼的密度，2p為鋼中的縱波聲速；0為換能器表面的速度；f為焦平面所在位置且fwp1；r為瑞利距離且r=12/2，11為水中的波數，12p為鋼中的波數；B=B+iD/F為聚焦換能器的高斯聲束系數，A和B分別為Wen和Breazeale系數[18]。從圖3(b)可知：有限元計算獲得的焦平面處徑向聲壓分布與多元高斯聲束模型得到的徑向聲壓分布基本完全一致，說明了本文有限元方法的有效性。

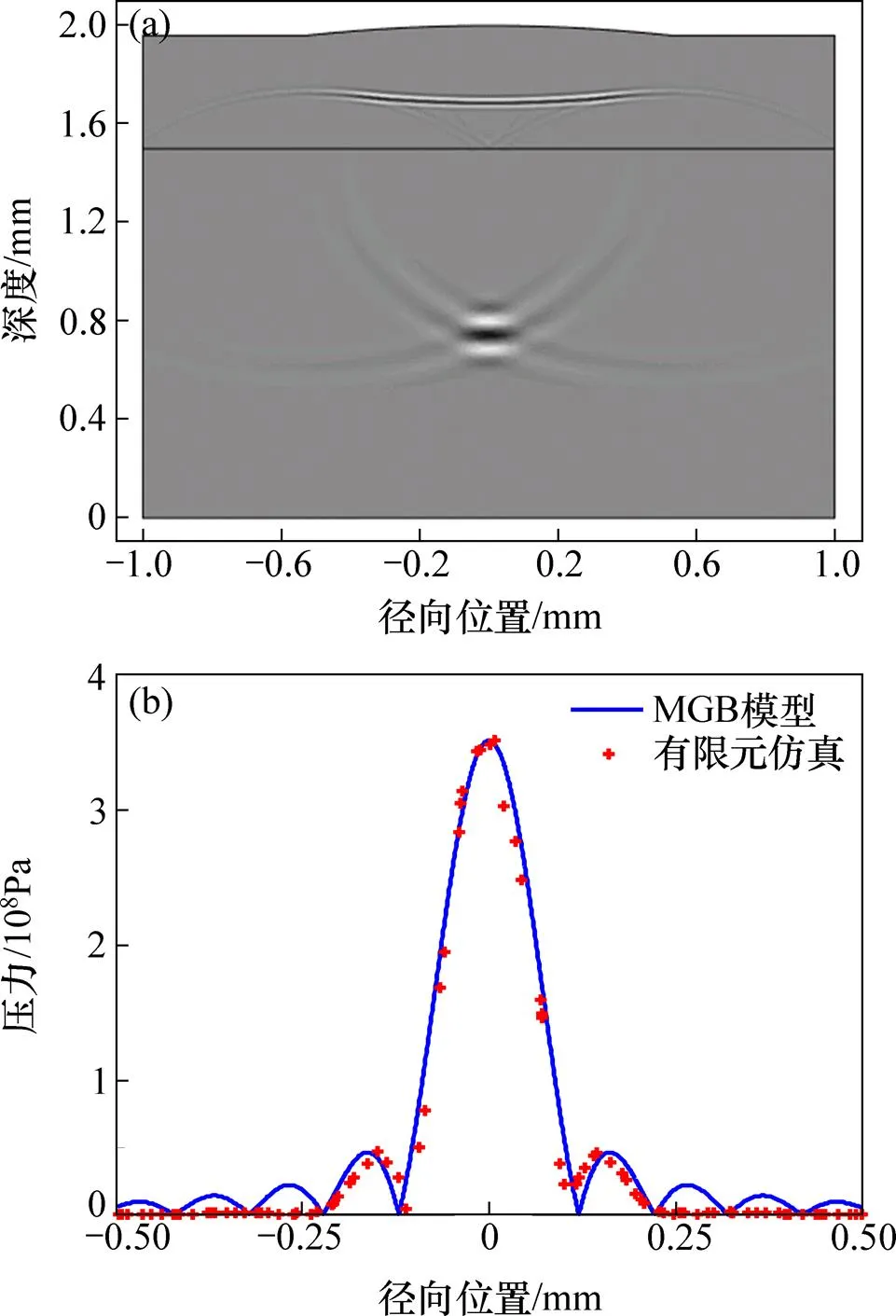
(a) 水?鋼兩相介質中的瞬態聲場分布；(b) 有限元計算

2 計算結果與分析

對含有不同厚度和不同深度夾雜物的反射回波，分別提取4個時域超聲特征參量和4個頻域特征超聲參量，分析超聲參量隨夾雜物厚度和夾雜物深度的變化規律。由于2次回波的波形更為復雜，因此，主要采用1次回波進行超聲特征參量計算。時域超聲參量包括：縱波聲速p、衰減系數、1次缺陷回波正峰值d和1次底面回波正峰值b。其中，縱波聲速p的表達式為

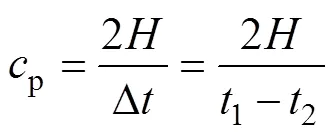
其中：為金屬板厚度；1為界面波的峰值對應的時刻；2為1次底面回波的峰值對應的時間。衰減系數的表達式為[19]

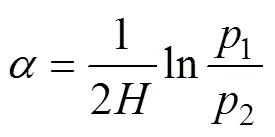
其中：1為1次底面回波的正峰值；2為二次底面回波的正峰值。衰減系數越小，說明衰減越嚴重。缺陷回波正峰值d表達式為

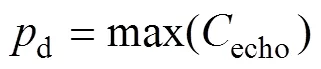
其中：echo為1次缺陷回波。底面回波正峰值b表達式為

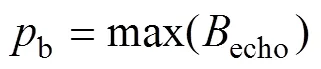
其中：echo為1次底面回波。

頻域超聲特征參量包括：一次底面回波峰值頻率p和一次底面回波?6 dB頻譜帶寬b。其中，回波信號的峰值頻率P為幅頻曲線最大幅值處對應的頻率，回波信號?6 dB頻譜帶寬b為幅頻曲線最大幅值50%處的橫線與頻譜曲線2個交點之間的頻率差。

2.1 不同厚度夾雜物的超聲參量特性

保持夾雜物的深度=0.75 mm不變，改變夾雜物的厚度為0.05，0.08，0.11，0.14，0.17，0.20和0.23 mm，計算獲得材料上表面反射回波并分別提取時域和頻域超聲參量。=0.05 mm和=0.17 mm的3種不同類型夾雜物，材料上表面接收到的反射回波信號，如圖4所示。從圖4可知：在界面波和一次底面回波之間、一次底面回波和二次底面回波之間，可以觀察到明顯的缺陷回波。二次缺陷回波和二次底面回波的幅值明顯低于一次缺陷回波和一次底面回波幅值，且時間展寬增大，表明經過多次反射后，超聲波發生了衰減和散射。從圖4還可知：不同厚度的同類夾雜物，其缺陷回波和底面回波的幅值、波形均有所差異。

對3種類型夾雜物，計算獲得的時域超聲參量隨夾雜物尺寸的變化關系曲線，如圖5所示。其中，橫坐標為夾雜物尺寸，定義為夾雜物厚度與波長的比值。圖5(a)中，含夾雜物鋼材的理論聲速計算公式為

其中：i為夾雜物中的縱波聲速，如表1所示。從圖5(a)可知：仿真計算獲得的聲速與理論計算結果基本完全一致，仿真結果稍大于理論值。這是由于式(6)的理論聲速假設波遇到夾雜物時的傳播路徑為直線，而實際超聲波遇到夾雜物時會繞射，傳播路徑為曲線，引起聲速增大。

從圖5(a)可知：不同類型夾雜物，縱波聲速均隨著夾雜物尺寸呈線性遞增，夾雜物尺寸相同時，含有MnS夾雜物的聲速最小，含有Al2O3夾雜物的聲速最大。從表1可知：夾雜物的聲速均大于鋼基體的聲速，且有p(Al2O3)＞p(TiN)＞p(MnS)，因此，當鋼內部含有夾雜物時，通過超聲回波計算的聲速大于純鋼基體的聲速且聲速隨著夾雜物尺寸增大而遞增，含有Al2O3夾雜物的增速最快。因此，對于夾雜物的超聲檢測而言，當檢測回波的縱波聲速大于鋼基體聲速時，可以作為判定內部是否存在夾雜物的參考參量。

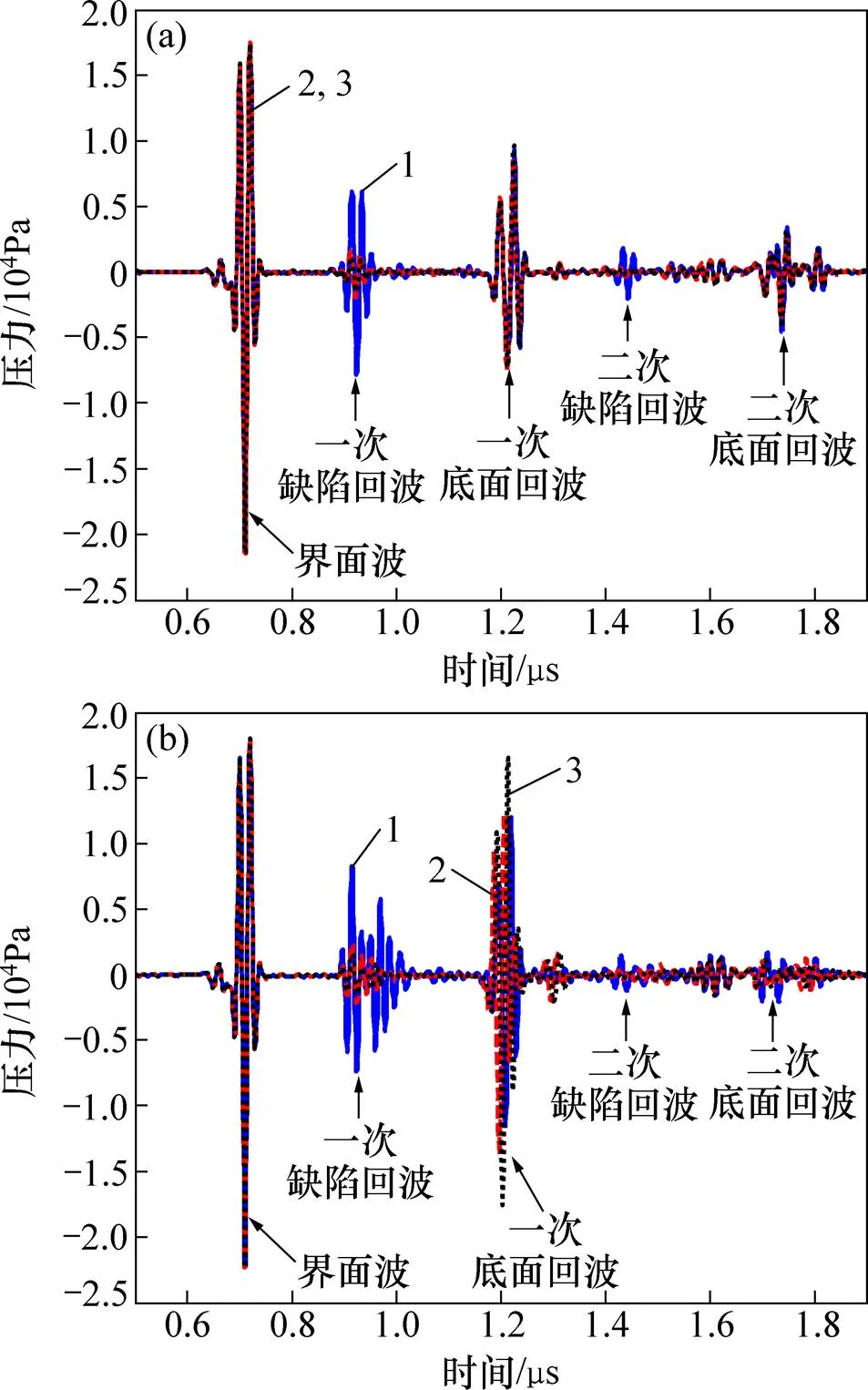
(a) D=0.05 mm；(b) D=0.17 mm

從圖5(b)可知：當鋼內含有MnS夾雜物時，衰減系數最小，引起的超聲衰減量最大；TiN夾雜物的衰減系數最大，引起的超聲衰減量最小。同時，不同類型夾雜物，衰減系數隨夾雜物尺寸均呈先增大后減小的變化規律，存在最大值。對Al2O3和TiN夾雜物，最大衰減系數對應的夾雜物尺寸/分別為1.42和1.66，即夾雜物厚度與聲波波長的比值約為1.5。對MnS夾雜物，最大衰減系數對應的夾雜物尺寸/=3.33，遠比Al2O3夾雜物和TiN夾雜物的大。

從圖5(c)可知：不同類型夾雜物的缺陷回波正峰值隨夾雜物尺寸均呈先減小后增大的變化規律，存在最小值，最小值對應的夾雜物尺寸/約為1，即當夾雜物厚度等于入射聲波的波長時，缺陷反射回波的幅值最小；當夾雜物厚度等于入射聲波的波長時，超聲波的繞射現象最嚴重，反射能力最弱，引起缺陷反射回波幅值最小。對不同類型的夾雜物，MnS夾雜物的聲阻抗與鋼基體聲阻抗差異最大，TiN夾雜物的聲阻抗與鋼基體的聲阻抗差異最小，因而，MnS夾雜物的缺陷反射回波幅值最大，TiN夾雜物最小。從圖5(d)可知：不同類型夾雜物，底面回波的正峰值隨夾雜物尺寸增加遞增，含TiN夾雜物的底面反射回波幅值最大，含MnS夾雜物的反射回波幅值最小。

對圖4(a)所示=0.05 mm的不同類型夾雜物反射回波信號中的一次缺陷回波和一次底面回波進行快速傅里葉變換后的頻域曲線，如圖6所示。從圖6可知：對中心頻率為50 MHz、頻率范圍在20~80 MHz的入射超聲波，缺陷回波和底面回波的頻率范圍均為20~80 MHz，缺陷回波的峰值頻率大于50 MHz，底面回波的峰值頻率小于50 MHz。

對3種類型的夾雜物，分別對不同尺寸夾雜物底面回波的幅頻曲線進行頻域超聲參量計算，獲得的頻域超聲參量隨夾雜物尺寸的變化關系曲線如圖7所示。圖7(a)和7(b)所示的底面回波峰值頻率、底面回波帶寬隨夾雜物尺寸增加均呈先增大后減小的變化規律，存在最大值；最大值對應的夾雜物尺寸/分別為1.15和0.90，即當夾雜物厚度約等于入射聲波的波長時，底面反射回波的峰值頻率和帶寬均最大；對3種不同類型夾雜物，TiN夾雜物的峰值頻率和帶寬最大，MnS夾雜物最小，表明MnS夾雜物對入射聲波中心頻率和帶寬范圍頻率成分衰減最顯著。

上述時域和頻域超聲參量隨夾雜物尺寸的計算結果顯示：底面回波峰值、底面回波峰值頻率和帶寬均在夾雜物尺寸約為1時出現極值，即當夾雜物厚度與入射聲波波長相等時，超聲參量出現極值。該特性可以為超聲準確測定夾雜物厚度提供基礎。在實際檢測過程中，可以采用不同中心頻率的探頭測量獲取多個回波曲線，繪制不同的超聲參量隨入射波長的變化曲線，曲線的極值點對應的波長即為夾雜物的厚度。

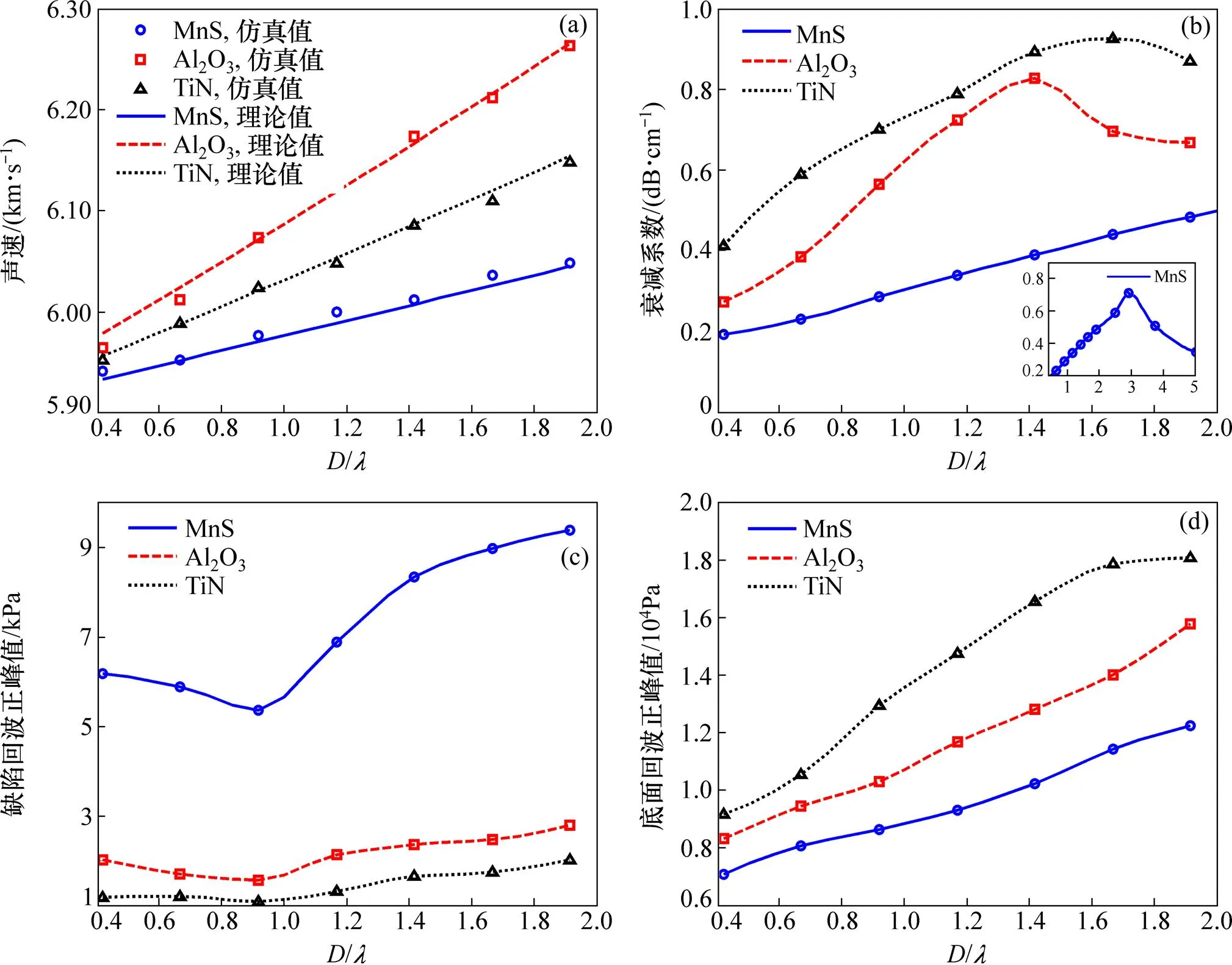
(a) 縱波聲速；(b) 衰減系數；(c) 缺陷回波正峰值；(d) 底面回波正峰值

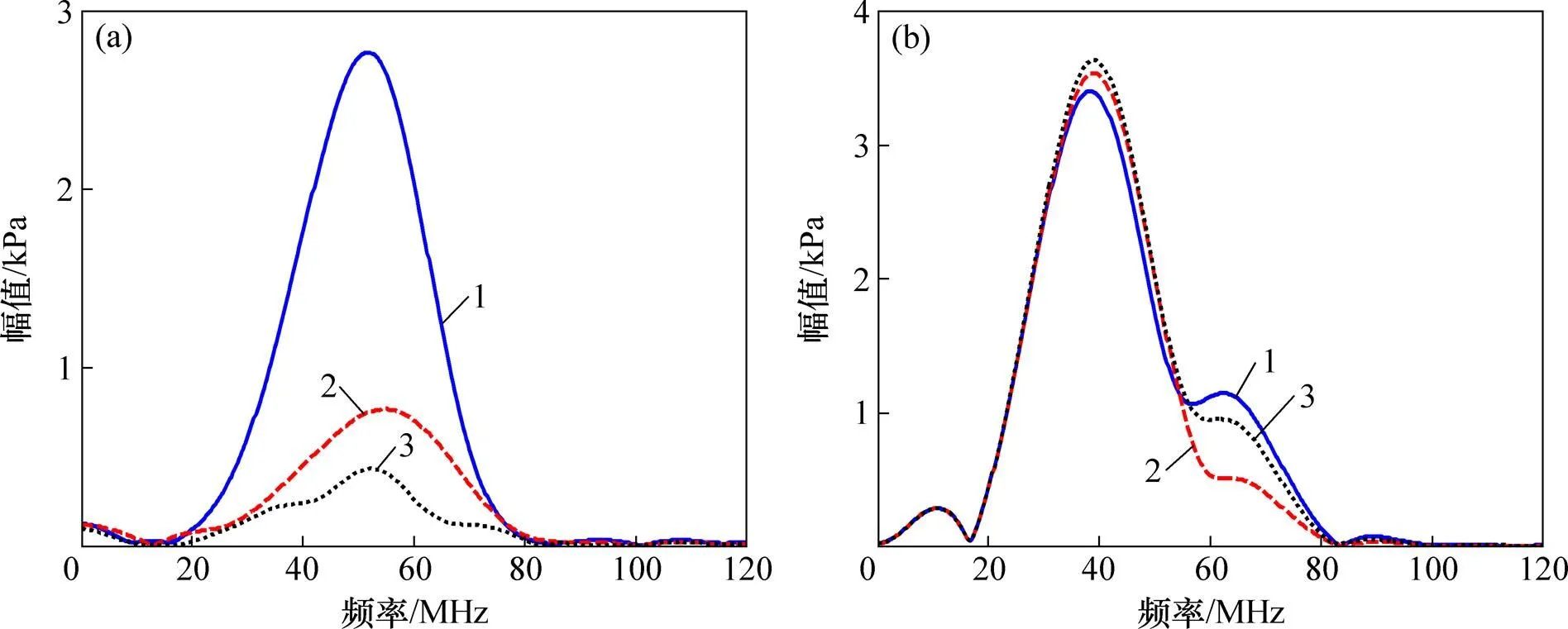
(a) 1次缺陷回波；(b) 1次底面回波

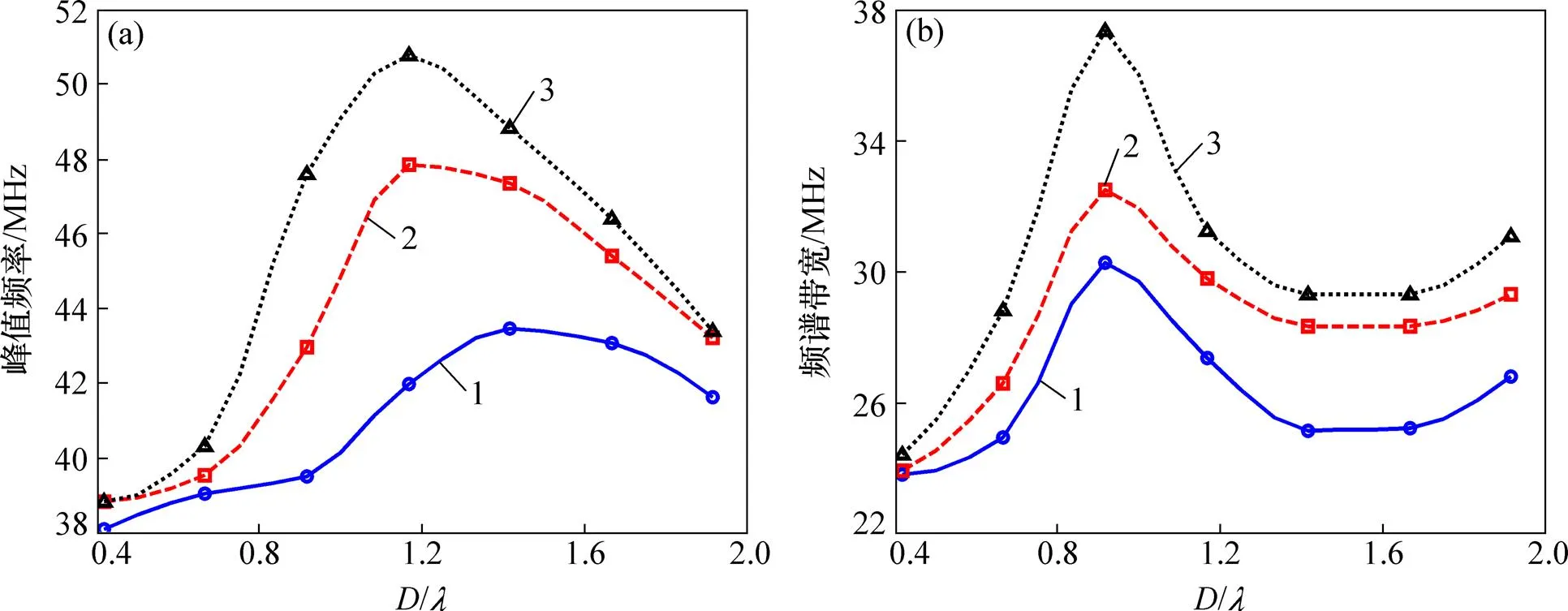
(a) 底面回波峰值頻率；(b) 底面回波?6 dB帶寬

2.2 不同深度夾雜物的超聲參量特性

保持夾雜物的厚度=0.10 mm不變，改變夾雜物深度為0.45，0.55，0.65，0.75，0.85和0.95 mm，計算獲得金屬板上表面反射回波并分別提取時域和頻域超聲參量。對于深度=0.45 mm和=0.75 mm的3種不同類型夾雜物，金屬板上表面接收到的反射回波信號如圖8所示。從圖8可知：當夾雜物深度變化時，缺陷回波到達的時間不同。根據缺陷回波與界面波的時間間隔，可以計算缺陷的深度位置。

對3種類型的夾雜物計算獲得的時域超聲參量隨夾雜物深度的變化關系曲線，如圖9所示。其中，橫坐標為夾雜物深度與鋼板厚度的比值。從圖9(a)可知：夾雜物深度變化時，縱波聲速保持不變。從圖9(b)可知：衰減系數隨夾雜物深度變化呈先減小再增大的變化規律，最小值出現在/=0.5，即當夾雜物位于板厚的中間時，衰減系數最小，衰減最嚴重；隨著夾雜物深度向上和向下偏離中心厚度，衰減系數逐漸增大，與圖5(b)所示結果一致，含TiN夾雜物時的衰減系數最大，含MnS夾雜物時的衰減系數最小，即MnS夾雜物引起的聲波幅值衰減最嚴重。從圖9(c)和9(d)可知：缺陷回波正峰值和底面回波正峰值均隨夾雜物深度的增加遞增，MnS夾雜物的缺陷回波幅值最大，而底面回波幅值最小，TiN夾雜物的缺陷回波幅值最小，而底面回波幅值最大。

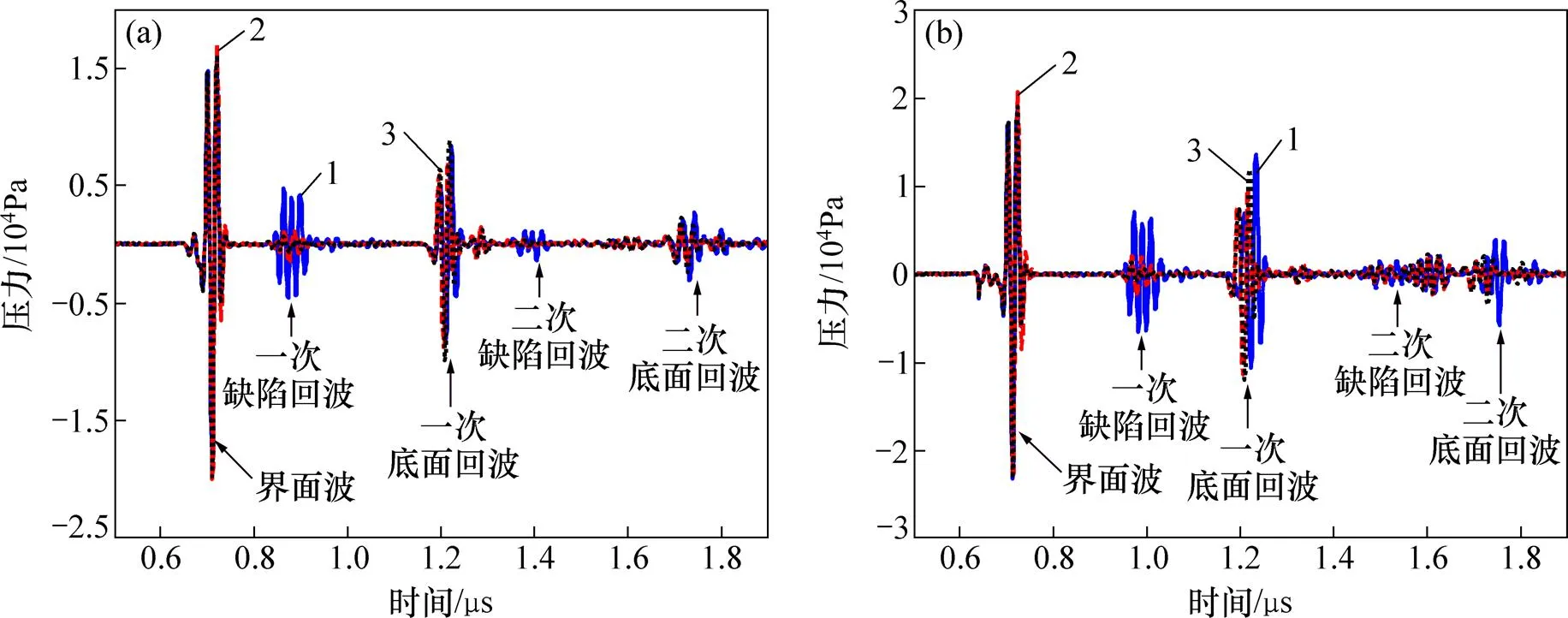
(a) h=0.45 mm；(b) h=0.75 mm

(a) 縱波聲速；(b) 衰減系數；(c) 缺陷回波正峰值；(d) 底面回波正峰值

對3種類型的夾雜物，計算獲得的頻域超聲參量隨夾雜物深度的變化關系曲線如圖10所示。從圖10(a)和(b)可知：隨著夾雜物深度增加，底面回波的峰值頻率和帶寬均存在最小值，最小值對應的夾雜物深度/=0.5，即當夾雜物位于板厚的中間時，夾雜物對入射聲波中心頻率和帶寬范圍頻率成分的衰減最顯著，這與圖9(b)所示的/=0.5對應最大衰減一致。

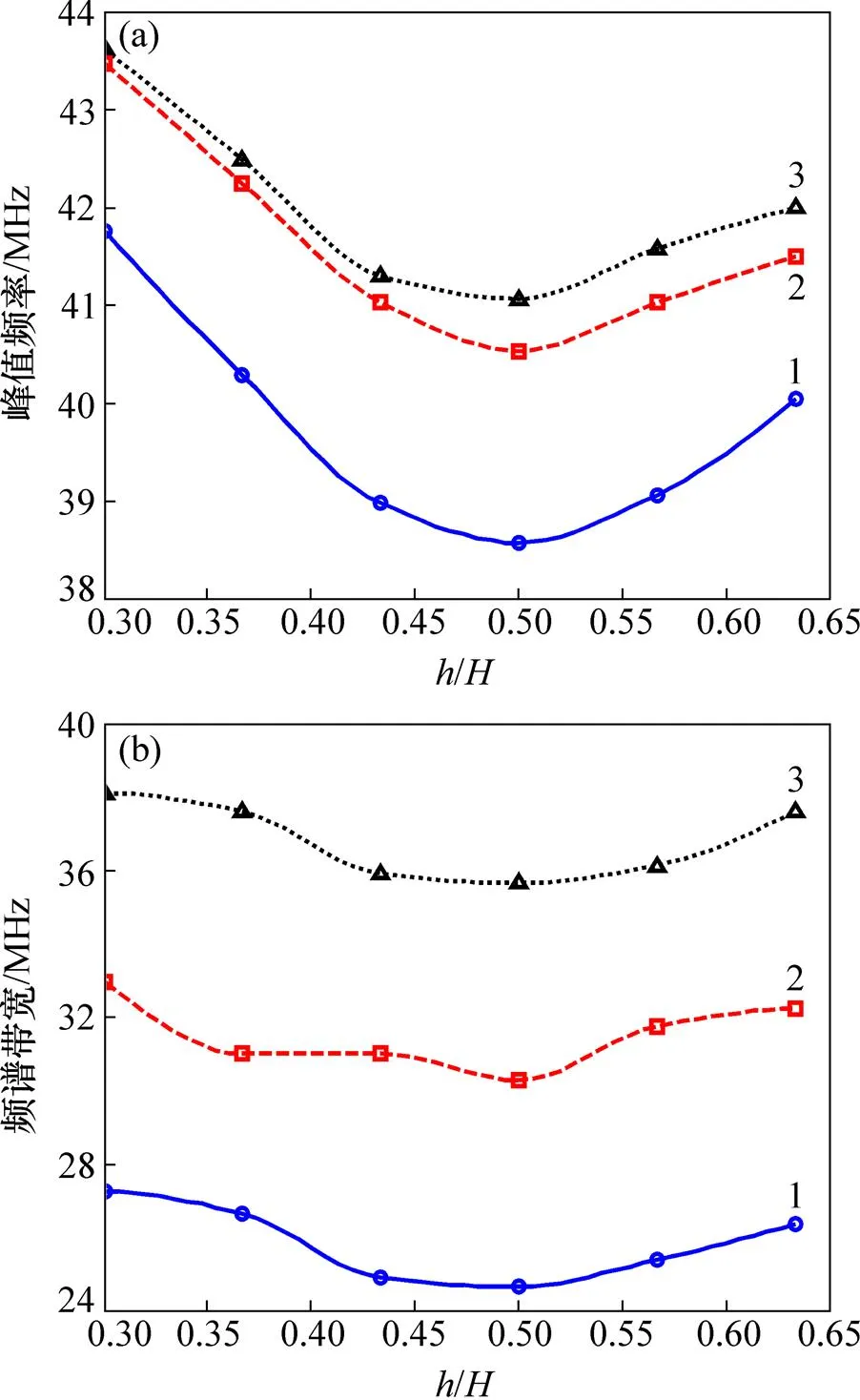
(a) 底面回波峰值頻率；(b) 底面回波?6 dB帶寬

3 實驗測試

為了進一步驗證上述仿真計算結果的準確性，采用超聲掃描顯微鏡裝置PVA SAM300對厚度為1.5 mm的2個鍍鋅板樣品進行超聲掃描實驗測試。與仿真計算條件保持一致，實驗測試選取的探頭為中心頻率50 MHz，晶片直徑3 mm，幾何焦距10 mm的水浸式點聚焦探頭。實驗數據的采樣頻率為5 GHz，對應的時間間隔為0.2 ns，與仿真計算的時間步長0.2 ns相同。機械掃查機構的掃描步進精度為3 μm。樣品1號內部不同深度檢測到3個缺陷，不同深度缺陷的時域波形如圖11所示。不同深度缺陷的缺陷回波與界面波之間的時間間隔()分別為0.231，0.304和0.382 μs，計算獲得的缺陷深度()分別為0.66，0.87和1.04 mm。缺陷的深度和最大長度如表2所示。其中，缺陷的最大長度采用C掃圖像的?6 dB下降法確定[20?21]。

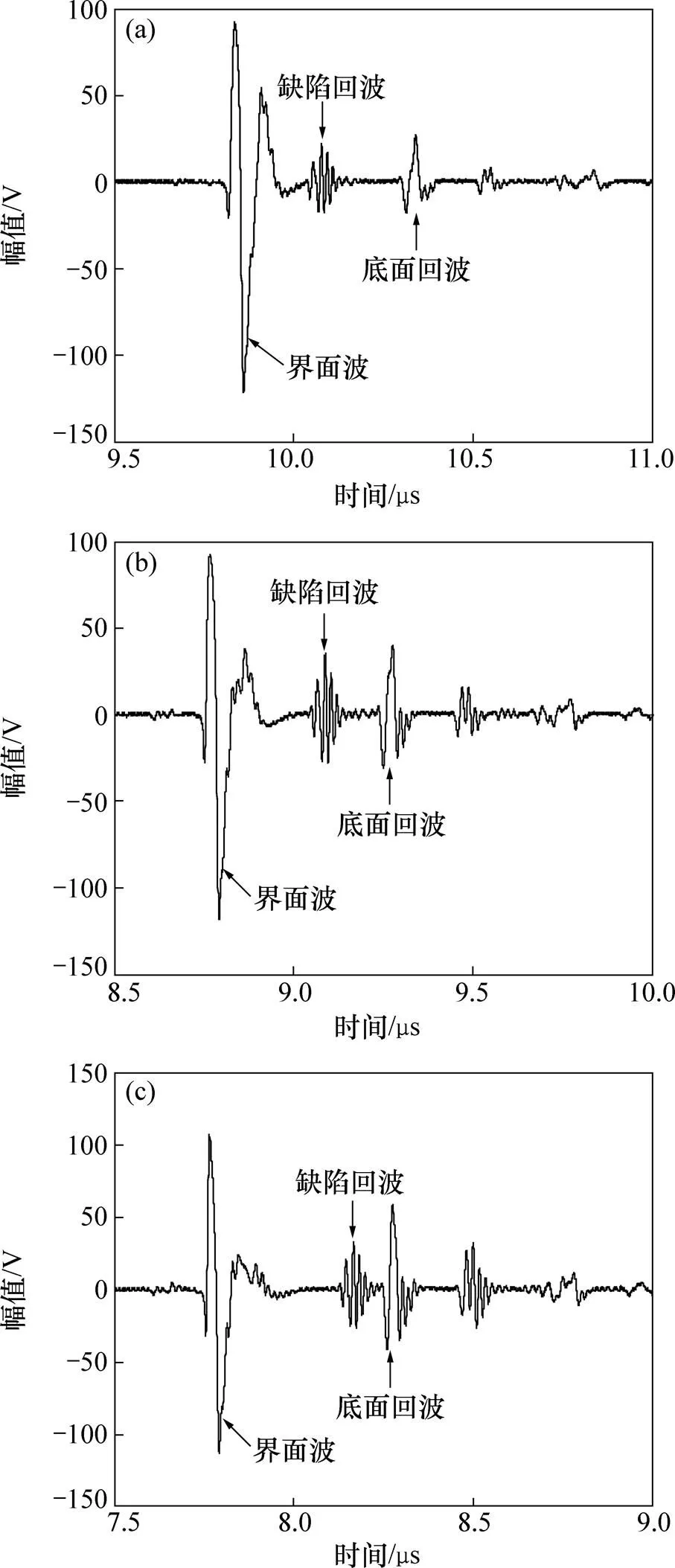
h/mm：(a) 0.66；(b) 0.87；(c) 1.04

為了進一步驗證超聲檢測的缺陷是否為夾雜物并判定夾雜物的類型，對超聲檢測后的樣品進行切割、打磨和拋光處理，使缺陷暴露于表面，用掃描電子顯微鏡(SEM)觀察并進行能譜分析，結果如圖12所示。其中，Al元素和O元素的原子數分數分別為36.75%和52.21%，原子數之比約為2:3，能譜結果顯示夾雜物的類型為Al2O3。

表2 1號樣品實驗測試的缺陷深度與最大長度

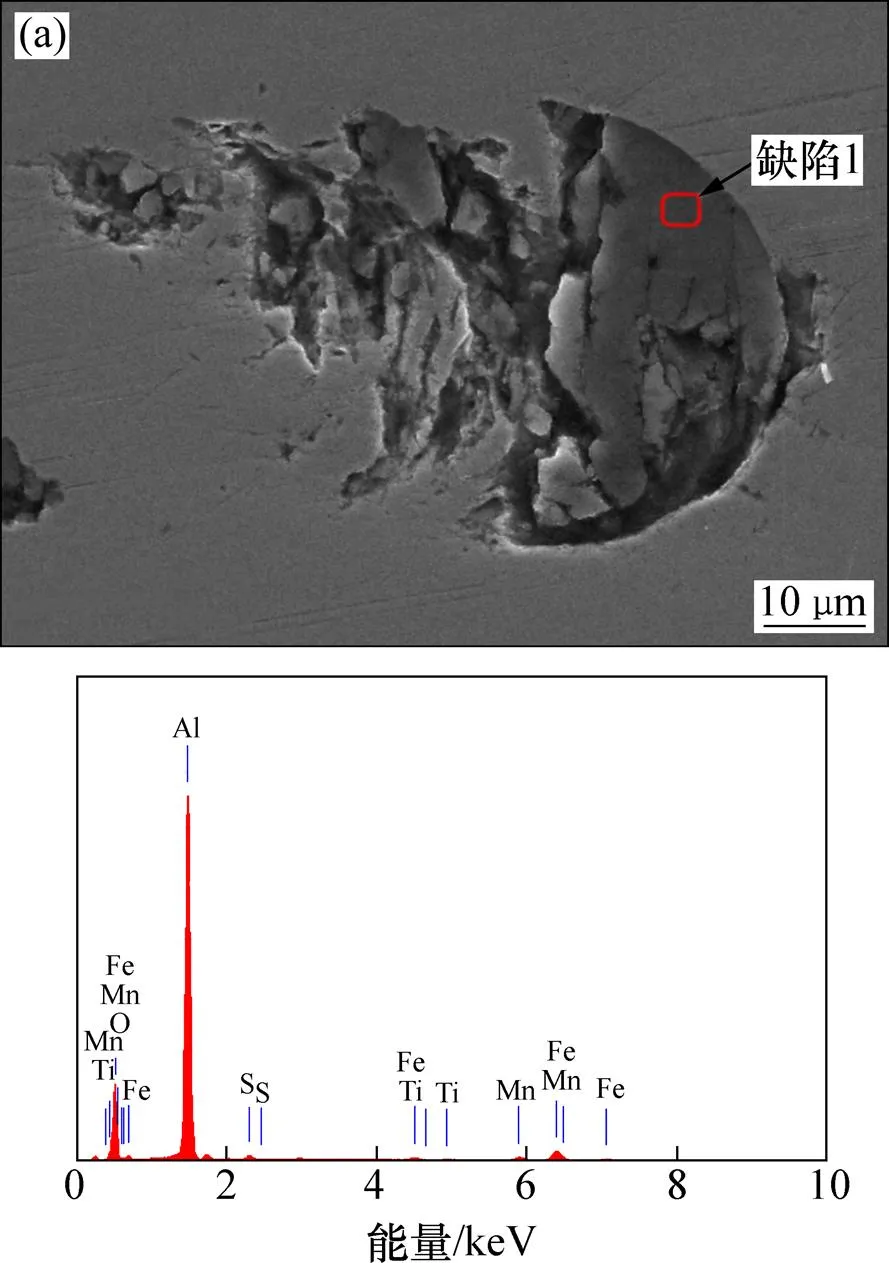
(a) 掃描電鏡圖；(b) 能譜分析

從表2所示的實驗結果可知：樣品1號中檢測到的3個夾雜物尺寸差異較小，而深度差異較大。因此，對樣品1號不同深度Al2O3夾雜物的時域波形進行縱波聲速特征值和衰減系數計算，并與圖9(a)和9(b)的仿真計算結果進行對比，如圖13所示。從圖13可知：實驗測試計算的聲速和衰減系數與仿真計算結果具有較好的一致性，證明了仿真計算結果的正確性。同時，仿真計算獲得的夾雜物的類型、厚度和深度等屬性特征對超聲測量信號的影響規律可為實際非金屬夾雜物的超聲檢測提供基礎與參考。

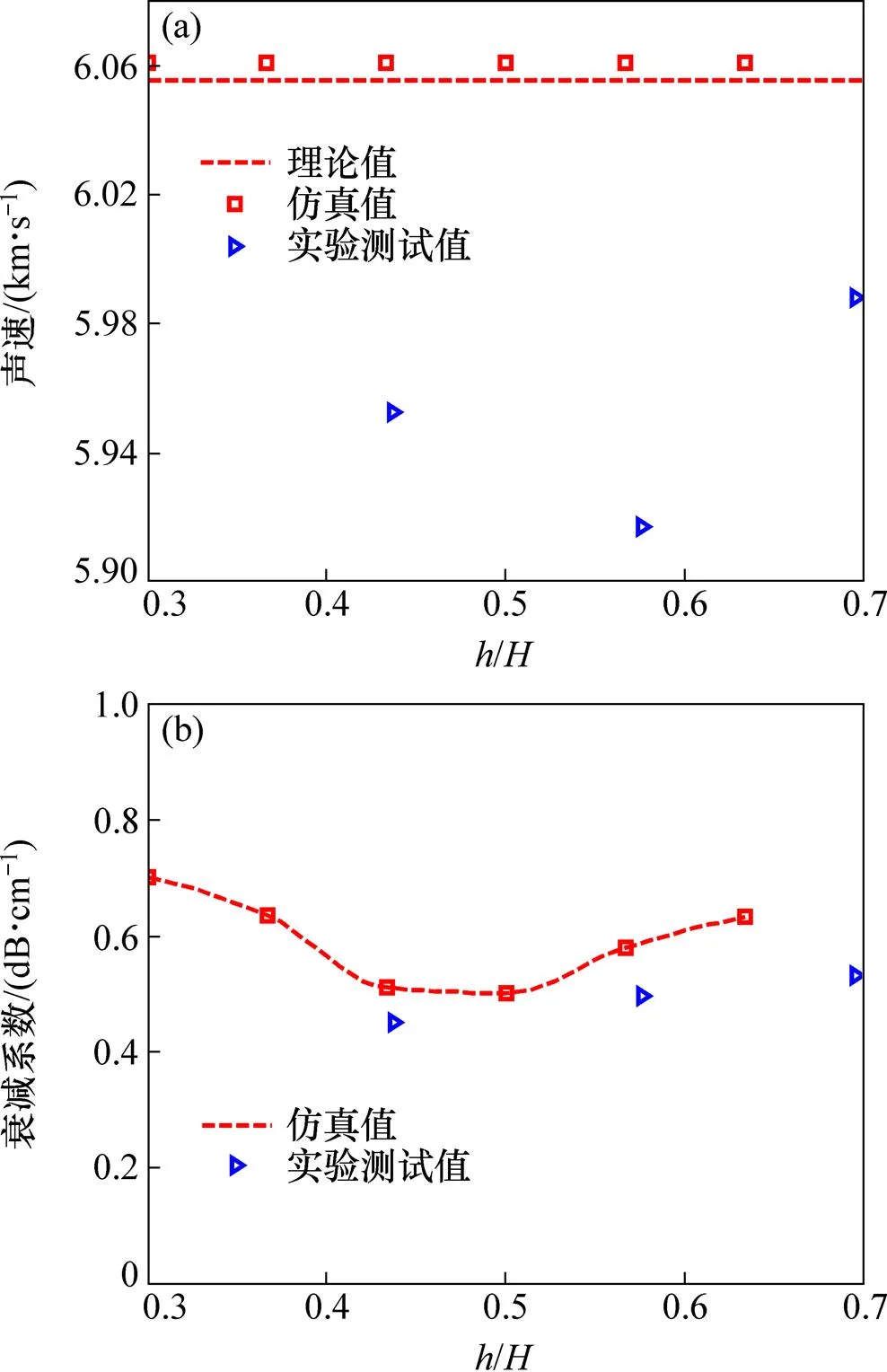
(a) 聲速；(b) 衰減系數

4 結論

1) 當鋼材內部存在夾雜物時，縱波聲速隨夾雜物尺寸的增加呈線性遞增，而不隨夾雜物的深度變化。含有Al2O3夾雜物的聲速最大且增速最快，含有MnS夾雜物的聲速最小且增速最慢，縱波聲速可以作為判定內部是否存在夾雜物的參量。

2) 當夾雜物厚度與入射聲波波長相等時，時域和頻域超聲參量均出現極值。該特性可以為超聲準確測定夾雜物尺寸提供基礎。在實際檢測過程中，可以采用不同中心頻率的探頭測量獲取多個回波曲線，繪制不同超聲參量隨入射波長的變化曲線，曲線的極值點對應的波長即為夾雜物的厚度。

3) 當夾雜物深度位于鋼板厚度的中間時，衰減系數和底面回波頻域參量均出現極值，衰減系數最大，夾雜物對入射聲波中心頻率和帶寬范圍頻率成分的衰減最顯著，且含有MnS夾雜物引起的聲波幅值衰減最嚴重，含有TiN夾雜物的聲波幅值衰減最小。

[1] GIRAULT J M, MéNIGOT S. Contrast optimization by metaheuristic for inclusion detection in nonlinear ultrasound imaging[J]. Physics Procedia, 2015, 70(1): 614?617.

[2] MEISNER L L, MARKOV A B, PROSKUROVSKY D I, et al. Effect of inclusions on cratering behavior in TiNi shape memory alloys irradiated with a low-energy, high-current electron beam[J]. Surface and Coatings Technology, 2016, 302: 495?506.

[3] 王新華, 李金柱, 姜敏, 等. 高端重要用途特殊鋼非金屬夾雜物控制技術研究[J]. 煉鋼, 2017, 33(2): 50?56. WANG Xinhua, LI Jinzhu, JIANG Min, et al. Investigation on technology of non-metallic inclusion control for high grade special steels of important uses[J]. Steelmaking, 2017, 33(2): 50?56.

[4] 馬超, 羅海文. 掃描電鏡和電解萃取法用于超潔凈鋼中夾雜物的表征[J]. 冶金分析, 2017, 37(8): 1?8. MA Chao, LUO Haiwen. Inclusion particles of super-clean steel examined by both scanning electron microscope and electrolytic extraction[J]. Metallurgical Analysis, 2017, 37(8): 1?8.

[5] 陳興富, 董國卿, 孫建勛, 等. 離心鑄造高鎳鉻復合軋輥中夾雜物分析[J]. 鑄造, 2017, 66(11): 1213?1219. CHEN Xingfu, DONG Guoqing, SUN Jianxun, et al. Analysis of inclusions in high Nickel-chrome composite roll enhanced by centrifugal casting[J]. Foundry, 2017, 66(11): 1213?1219.

[6] 楊鋒功, 楊華峰, 戰東平, 等. 鋼包軟吹氬時間對GCr15 軸承鋼中夾雜物的影響[J]. 材料與冶金學報, 2017, 16(4): 246?249. YANG Fenggong, YANG Huafeng, ZHAN Dongping, et al. Effect of ladle soft argon blowing time on inclusions of GCr15 bearing steel in tundish[J]. Journal of Materials and Metallurgy, 2017, 16(4): 246?249.

[7] 劉瀏, 范建文, 王品, 等. 軸承鋼精煉中大型夾雜物來源的示蹤[J]. 鋼鐵, 2017, 52(9): 34?41. LIU Liu, FAN Jianwen, WANG Pin, et al. Generation mechanism of large inclusions during bearing steels refining process by tracer method[J]. Iron and Steel, 2017, 52(9): 34?41.

[8] MOGHADDAM S M, SADEGHI F, PAULSON K, et al. A 3D numerical and experimental investigation of microstructural alterations around non-metallic inclusions in bearing steel[J]. International Journal of Fatigue, 2016, 88: 29?41.

[9] MEZIL S, CHIGAREV N, TOURNAT V, et al. Evaluation of crack parameters by a nonlinear frequency-mixing laser ultrasonics method[J]. Ultrasonics, 2016, 69: 225?235.

[10] 陳振華, 史耀武, 趙海燕, 等. 微小缺陷的非線性超聲檢測及其成像技術[J]. 聲學學報, 2010, 35(1): 9?13. CHEN Zhenhua, SHI Yaowu, ZHAO Haiyan, et al. Nonlinear ultrasonic testing and imaging for tiny flaw[J]. Acta Acustica, 2010, 35(1): 9?13.

[11] 劉增華, 余鋒祥, 于洪濤, 等. 基于群速度校準的超聲導波技術及在復合材料缺陷檢測中的應用[J]. 機械工程學報, 2012, 48(20): 8?15. LIU Zenghua, YU Fengxiang, YU Hongtao, et al. Ultrasonic guided wave technology based on group velocity calibration and its application for defect detection in composite plates[J]. Journal of Mechanical Engineering, 2012, 48(20): 8?15.

[12] 宋雨珂, 汪小凱, 華林. 軸類零件內部缺陷超聲檢測與重構方法研究[J]. 應用聲學, 2016, 35(2): 109?115. SONG Yuke, WANG Xiaokai, HUA Lin. Research on ultrasonic test and reconstruction method of the internal defects in shaft parts[J]. Journal of Applied Acoustics, 2016, 35(2): 109?115.

[13] 王國承. 鋼中夾雜物尺寸控制理論與技術[M]. 北京: 冶金工業出版社, 2015: 5?10. WANG Guocheng. Size control theory and technology of inclusion in steel[M]. Beijing: Metallurgical Industry Press, 2015: 5?10.

[14] BELLIS C, BONNET M. Qualitative identification of cracks using 3D transient elastodynamic topological derivative: formulation and FE implementation[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 253: 89?105.

[15] LI R, NATSUKI T, NI Q Q. A novel dynamic stress analysis in bimaterial composite with defect using ultrasonic wave propagation[J]. Composite Structures, 2015, 132: 255?264.

[16] KIM S J, SONG S J, SCHMERR L W. Modeling ultrasonic pulse-echo signals from a flat-bottom hole in immersion testing using a multi-Gaussian beam[J]. Journal of Nondestructive Evaluation, 2004, 23: 11?19.

[17] XIAO Huifang, SUN Yunyun, CHEN Dan, et al. Prediction of flat-bottom hole signals received by a spherically focused transducer for an ultrasonic pulse echo immersion testing[J]. Measurement Science and Technology, 2016, 27: 115001-1-11.

[18] WEN J J, BREAZEALE M A. A diffraction beam field expressed as the superposition of Gaussian beams[J]. Journal of the Acoustical Society of America, 1988, 83(5): 1752?1756.

[19] NURUL I M, ARAI Y, ARAKI W. Initiation of fatigue crack growth in austenitic stainless steel detected by ultrasound: role of in-plane orientation[J]. Materials Science and Engineering: A, 2012, 556(11): 309?318.

[20] YANG S, YOON B, KIM Y. Using phased array ultrasonic technique for the inspection of straddle mount-type low-pressure turbine disc[J]. NDT & E International, 2009, 42(2): 128?132.

[21] SONG Yongfeng, WANG Yiling, NI Peijun, et al. Flaw sizing method based on ultrasonic dynamic thresholds and neural network[J]. AIP Conference Proceedings, 2016, 1706: 180007-1-9.

(編輯 楊幼平)

Effect of embedded inclusion in steel on ultrasonic parameters in time frequency domain

XIAO Huifang1, CHEN Dan2, XU Jinwu2

(1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China; 2. Collaborative Innovation Center of Steel Technology, University of Science and Technology Beijing, Beijing 100083, China)

A numerical analytical model of two-dimensional isotropic plate with embedded inclusion was established, andthe variation of ultrasonic signals with the depth, thickness and type of inclusions was studied. The validity of the model was verified using experimental results from ultrasonic microscope measurement and scanning electron microscope. The results show that the longitude sound velocity increases linearly with the thickness of inclusion. The Al2O3inclusion has the largest sound velocity and the fastest increasing rate, while the sound velocity of MnS inclusion has the smallest sound velocity and the slowest rising rate. The longitudinal sound velocity can be used to determine the existence of inclusion. The relationship between different ultrasonic parameters and incident wavelength can be used to determine the thickness of inclusions. When the inclusion is at the center of the steel plate, the attenuation coefficient has the maximum value, and the attenuation of MnS inclusion is the maximum, while the attenuation of TiN inclusion is the minimum.

inclusion; ultrasonic parameters; numerical simulation; multi-domain; influence effect

10.11817/j.issn.1672?7207.2018.10.003

TH14

A

1672?7207(2018)10?2381?10

2017?11?07；

2018?03?02

國家“十二五”科技支撐計劃項目(2015BAF30B00)；國家自然科學基金資助項目(51775037)(Project(2015BAF30B00) supported by the National Science and Technology Program of China during the 12th Five-Year Plan Period; Project(51775037) supported by the National Natural Science Foundation of China)

肖會芳，博士，副教授，從事材料超聲無損檢測技術研究；E-mail：huifangxiao@ustb.edu.cn