一種新型低分子熱塑性樹脂體系CBT500/DBTL的界面張力表征

付繼先，吳旺青，劉毅，蔣炳炎

?

一種新型低分子熱塑性樹脂體系CBT500/DBTL的界面張力表征

付繼先1, 2，吳旺青1, 2，劉毅1, 2，蔣炳炎1, 2

(1. 中南大學 機電工程學院，湖南 長沙，410083； 2. 中南大學 高性能復雜制造國家重點實驗室，湖南 長沙，410083)

為獲得真實、可靠的新型低分子熱塑性樹脂體系CBT500(環對苯二甲酸丁二醇酯)/DBTL(二月桂酸二丁基錫)的界面張力，研究新型樹脂體系的混合機理及指導混合設備研制，綜合接觸角法與調和平均法的各自優勢，依據相似理論，提出引用調和平均法修正接觸角法，首先研究20~120 ℃范圍內CBT500/DBTL樹脂體系的界面張力。其次采用最小二乘法分段線性擬合界面張力修正值并推廣。研究結果表明：在20~120℃范圍內，CBT500/DBTL樹脂體系的界面張力隨溫度的升高而降低。與接觸角法獲得的界面張力計算值相比，采用調和平均法獲得的界面張力修正值整體減小44.7%，更加接近真實值。得到20~200 ℃范圍內，CBT500/DBTL樹脂體系界面張力與溫度之間的分段函數關系式。

原位聚合注射成型；界面張力；調和平均法；接觸角法；相似理論

原位聚合注射成型是高性能連續纖維熱塑性復合材料先進制造技術的發展前沿[1]。低分子熱塑性樹脂原位聚合注射成型工藝，與熱塑性樹脂傳遞模塑成型(T-RTM)工藝類似，主要包括4個階段：1) 低分子熱塑性樹脂和催化劑混合；2) 混合樹脂體系注射、浸漬密閉模具型腔中的連續纖維預制體；3) 混合樹脂體系在一定的溫度下，在密閉的模具型腔中發生原位聚合反應，形成高分子熱塑性樹脂基體；4) 連續纖維熱塑性復合材料零件脫膜。近年來，國內外學者對原位聚合注射成型技術進行了廣泛研究[2?3]，側重點主要集中在樹脂配方、注射工藝、原位聚合反應條件與復合材料性能表征等方面。針對低分子熱塑性樹脂與催化劑的混合過程及其對復合材料制件性能的影響研究較少。樹脂體系的混合過程主要是指將一定比例的分散相固態粉末或液態催化劑引入連續相低分子熱塑性樹脂熔體，再通過專門的混合裝置中設置的混料芯結構，實現催化劑與樹脂的混合。原位聚合反應中，低分子熱塑性樹脂和催化劑的混合質量與復合材料樹脂基體的高分子聚合相對分子質量、均勻性密切相關，嚴重影響復合材料的力學、機械等性能[3?5]。催化劑與樹脂間的界面張力決定混合過程中催化劑的破碎形態、顆粒度等參數，是影響樹脂體系混合質量的重要因 素[6?7]。因此，界面張力的研究對于新型樹脂體系的混合方式選擇與混合設備研制具有重要意義。CBT500與DBTL是適用于低分子熱塑性樹脂原位聚合注射成型工藝的新型樹脂體系。室溫條件下，DBTL為淺黃色油狀液體，CBT500為白色顆粒，熔點為120~170 ℃。原位聚合物注射成型中，常溫DBTL與CBT500熔體在170~200 ℃條件下混合時，二者之間既沒有明顯界面、又面臨高溫挑戰，導致DBTL與CBT500樹脂體系的界面張力表征困難，目前還未見相關研究報道。國內外學者針對常規材料界面張力的表征進行了廣泛研究，根據表征方法是否伴隨有潤濕，界面張力測定方式主要分為2類：1) 有潤濕的測量方法有接觸角法[8]、表面張力分量法[9]等；2) 無潤濕的測量方式有滴重法[10]、懸滴法[11]、躺滴法[11]等。相較于有潤濕的測量方法，無潤濕測量方法精度更高，但對材料有特殊要求如：兩材料間有清晰界面輪廓，液滴軸對稱等。朱定一等[8]基于有限平面內液滴張力分布特性，得出了界面張力是液體表面張力和液體在測定薄板上靜態接觸角的函數，提出了應用接觸角法計算界面張力的方法。研究表明，在測定薄板熔化之前，液滴與測定薄板之間的靜態接觸角隨著測量溫度的升高而降低，采用接觸角法可以得到任一測量溫度下固液體系的界面張力。FOWKES[9]假設非色散力對界面張力無影響，提出了表面張力分量法，認為界面張力等于兩材料表面張力之和減去兩材料色散分力的幾何平均數。WU[12]通過極性化合物間界面張力研究發現，表面張力分量法只能獲得某一特定溫度下固液體系的界面張力，且界面張力的計算誤差高達50%~100%。于是他采用調和平均法對表張力分量法進行了改進，將計算誤差降低至1%以內。ZDZIENNICKA等[13?14]的研究進一步驗證了調和平均法的可靠性。綜合上述文獻報道，當固液體系的靜態接觸角大于35°時，接觸角法的優勢在于其可以得到任一測量溫度下的界面張力。而調和平均法的優勢在于其可以準確獲得某一特定溫度下固液體系的界面張力。當固液體系間的接觸角小于35°時，相較于接觸角法，采用調和平均法獲得的界面張力精度更高。針對新型CBT500/DBTL熱塑性樹脂體系間的潤濕特性預研表明，在20~120 ℃范圍內DBTL液滴在CBT500光滑薄板上的靜態接觸角均小于35°。因此，本文作者綜合接觸角法與調和平均法的各自優勢，依據相似理論，采用調和平均法修正接觸角法，分別獲得了20~120 ℃范圍內CBT500/DBTL固液體系的界面張力的計算值和修正值曲線。然后采用最小二乘法分段線性擬合并推廣，得到了20~200 ℃溫度范圍內，CBT500/DBTL樹脂體系界面張力與溫度之間的函數關系式。研究結果為進一步獲得CBT500/DBTL樹脂體系在原位聚合注射成型工藝條件下的界面張力，研究CBT500/DBTL樹脂體系的混合機理和設備研制提供了參考依據。

1 基本理論

1.1 接觸角法[8]

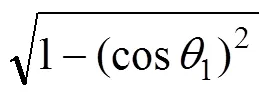
12=?1cos1，90°≤1≤180° (1)

2=1+sin1，90°≤1≤180° (2)

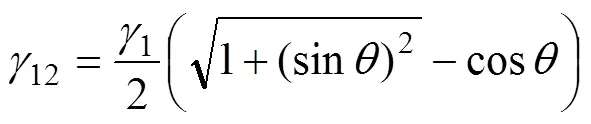
0°≤θ≤180° (3)

式中：12為固液界面張力，mN/m；1為液體表面張力，mN/m；2為固體表面張力，mN/m；1為液滴在有限平面內靜態接觸角，(°)；為液滴在無限平面內靜態接觸角，(°)。

1.2 調和平均法[12]

界面張力方程如式(4)所示，WU[12]認為?d和?p分別為相應材料的色散分量、極性分量倒數平均和，結合式(4)得到調和平均法方程式(5)。

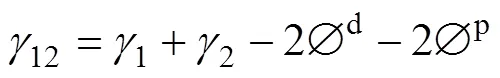
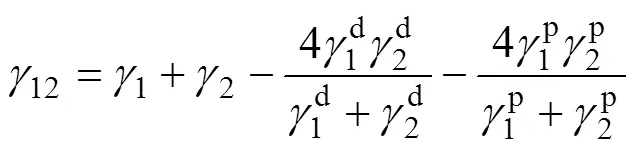
式中：下標1和2為兩組分；12為界面張力，mN/m；為表面張力，mN/m；?d為相互色散性，mN/m；?p為相互極性，mN/m；d為色散分量，mN/m；p為極性分量，mN/m。

由于材料的極性分量、色散分量、表面張力為未知常數，因此，至少需要2種已知表面張力、色散分量、極性分量的低分子測試液體，分別滴在固體光滑表面，測量相應靜態接觸角，將參數代入式(5)與Young方程12=2+1cos聯立得到的式(6)，才能獲得對應的極性分量、色散分量，由式(7)[14]計算表面張力。

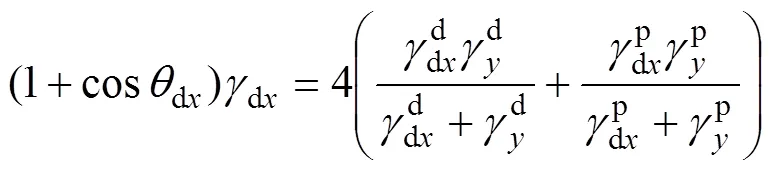
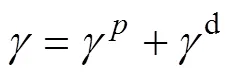
式中：和為1或2，取定值，為變量；為低分子；為接觸角，(°)；為表面張力，mN/m；d為色散分量，mN/m；p為極性分量，mN/m。將獲得的材料參數代入式(5)，求得最終兩物質界面張力。

1.3 相似理論

相似理論[15]是闡述自然或工程中相似現象的理論學說。其在解決工程和實驗問題中有廣泛的應用，TONG等[16]基于相似理論建立泄漏氣體濃度預測模型，這有利于減輕毒氣泄漏事故。相似理論數學模型如式(8)和(9)所示。原型條件為(壓強)、(密度)、…、(體積)、(黏度)，模型條件為1、1、…、1、1。不同溫度下原型與模型所對應的結果分別為Tx和Tx。當不同溫度下原型與模型條件都滿足式(8)時，不同溫度下原型與模型結果之比滿足式(9)，其中為結果比，為相似系數。

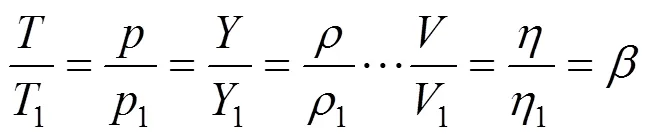
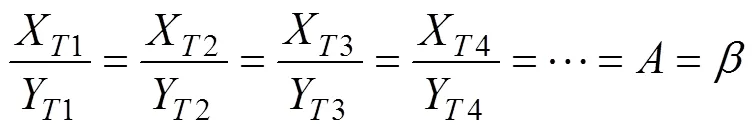
本文中原型與模型分別是指接觸角法與調和平均法，實驗材料及儀器相同，原型條件是測(測試溫度)、加(加熱時間)、靜(靜置時間)、(液滴體積)、(標準大氣壓)；模型條件是測1(測試溫度)、加1(加熱時間)、靜1(靜置時間)、1(液滴體積)、1(標準大氣壓)。當相似系數為1時，采用調和平均法修正接觸角法。

2 實驗部分

2.1 原料和儀器

原料有：CBT500顆粒，德國Cyclic Corporation，純度＞99%，熔點為120~170 ℃；DBTL，分析純，天津市風船化學試劑科技有限公司，錫質量分數為18%~20%，純度＞99%，分解溫度＞150 ℃；HD120MO型均聚物聚丙烯(PP)顆粒，北歐化工，純度＞99%，熱變形溫度為88 ℃；乙二醇，分析純，西隴化工股份有限公司，純度＞99%；自制蒸餾水。

儀器有：瑞典Biolin Scientific Theta光學接觸角測量儀、上海中晨JC2000D3靜態接觸角測量儀、東莞得力仕DSB?30油壓機、東莞宏展HH?138的精密烤箱、信易SCD?20μ/30H干燥機。

2.2 樣品制備

測定薄板分別由2種材料CBT500和PP制成，用于一定溫度下不同材料液滴在相應薄板上靜態接觸角的測量。采用抽真空熱壓工藝制備光滑薄板，成型工藝參數如表1所示，具體過程為：采用信易SCD?20μ/30H干燥機對CBT500和PP顆粒進行干燥，干燥溫度、時間分別為80 ℃和24 h。采用HH?138的精密烤箱對干燥后CBT500和PP顆粒分別進行預加熱，加熱溫度分別為140 ℃和160 ℃，加熱時間均為0.5 h。將預加熱CBT500和PP顆粒分別倒入溫度為130 ℃和150 ℃的模具中，采取抽真空熱壓工藝制備CBT500和PP光滑薄板。抽真空熱壓工藝包括6個階段：1) 動模降至密封圈；2) 抽真空；3) 施壓；4) 保壓；5) 冷卻；6) 開模取件。為獲得良好的密閉空間，動模應迅速下降至密封圈并微壓，如圖2(a)所示。抽真空后，施加壓力將CBT500和PP顆粒壓實，制成相應光滑薄板，如圖2(b)所示。

表1 壓縮成型工藝參數

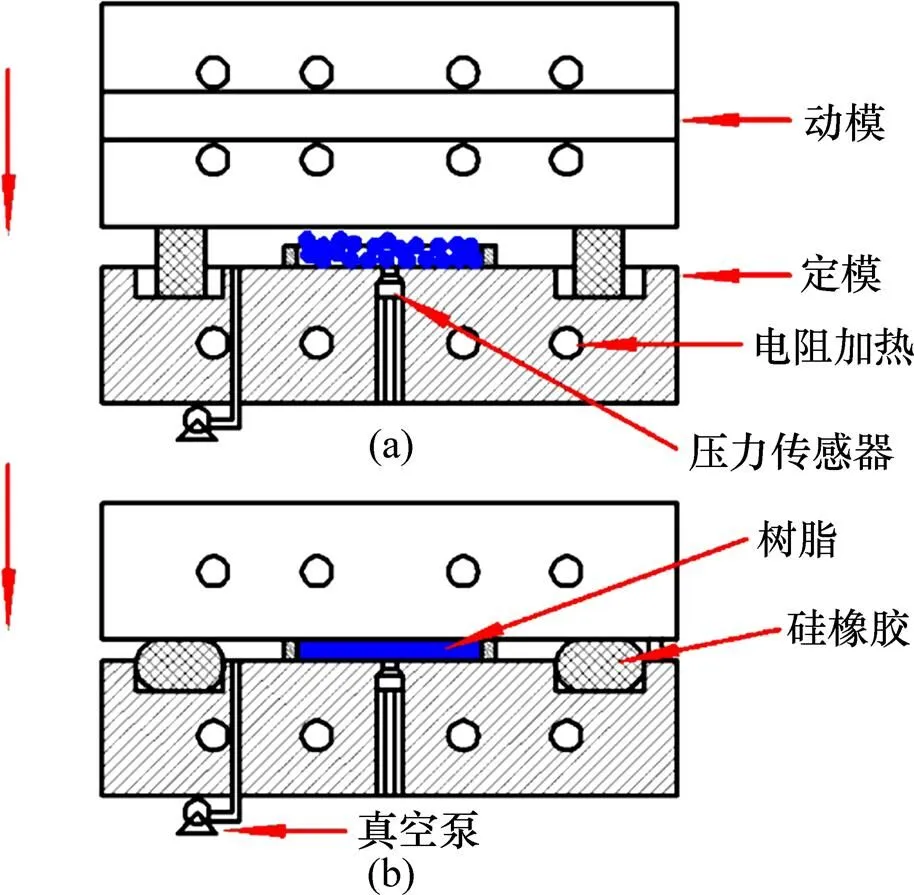
(a) 動模下降至密封圈后抽真空；(b) 施壓與保壓

2.3 實驗方案

2.3.1 DBTL表面張力表征

采用瑞典Biolin Scientific Theta光學接觸角測量儀的懸滴法測量20，40，60，80，100和120 ℃溫度下DBTL的表面張力。將DBTL緩慢從自制滴管中滴出，當液滴外形出現輕微縮頸時，保溫30 s，測量該狀態下表面張力，每個溫度點測5次求算術平均值作為該溫度下表面張力。

2.3.2 靜態接觸角測量

采用上海中晨JC2000D靜態接觸角測量儀的量角法測量不同溫度下不同固液體系的靜態接觸角，其中不同固液體系分別是CBT500/DBTL、CBT500/乙二醇、CBT500/蒸餾水、PP/乙二醇、PP/蒸餾水、PP/DBTL。將薄板放置在樣品臺上并加熱10 min，再緩慢滴下體積為2.5 μL[17]的測試液滴，靜置10 s，測量液滴在光滑薄板上靜態接觸角，每個溫度點測5次求算術平均值作為該溫度下靜態接觸角。

3 結果與討論

3.1 DBTL表面張力

對20，40，60，80，100和120 ℃溫度下DBTL的表面張力1進行測量，結果如圖3所示。由圖3可知：溫度在60 ℃和100 ℃時方差較大，隨溫度升高，DBTL表面張力減小，且線性關系明顯。DBTL密度隨溫度增加而降低，導致DBTL流動性提高，液滴易形成，此外，空氣密度低，溫度對空氣密度影響忽略不計，致使DBTL與空氣密度差減小，從而導致表面張力隨溫度增加而減小。

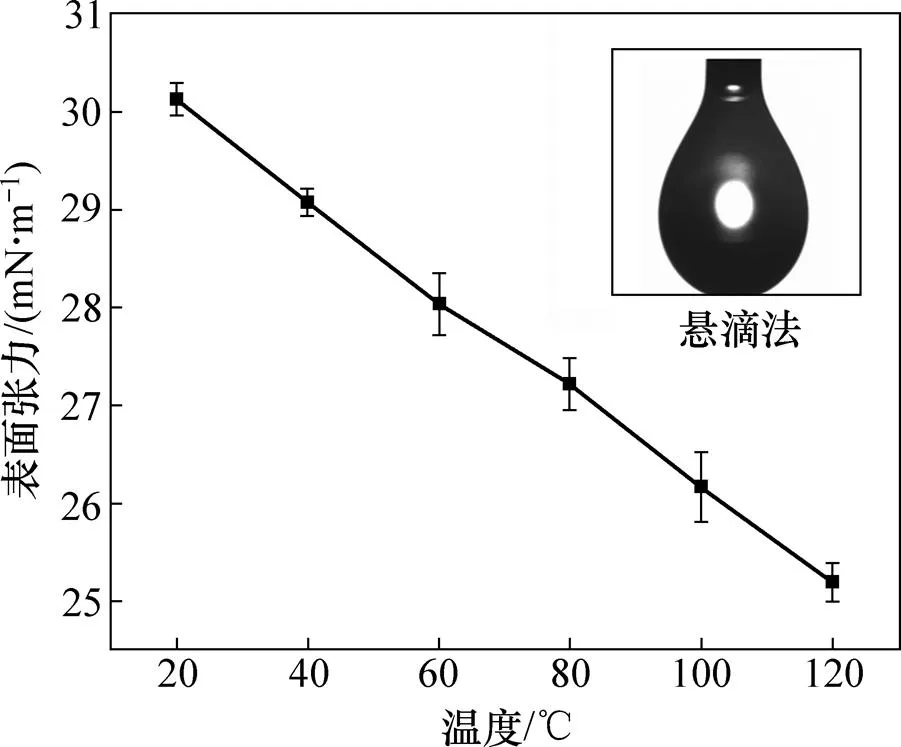
圖3 不同溫度下DBTL表面張力

3.2 不同溫度下接觸角法計算DBTL與CBT500界面張力

對20，40，60，80，100和120 ℃溫度下DBTL在CBT500光滑薄板上靜態接觸角進行測量，結果如圖4所示。結合上述溫度下DBTL界面張力1(如圖3所示)，將和1代入式(3)，計算相應溫度下DBTL與CBT500的接觸角法界面張力12，結果如圖4中界面張力所示。由圖4可知：隨著溫度升高，接觸角和接觸角法界面張力具有相同的下降規律，不同溫度區間內下降趨勢不同，20~60 ℃溫度區間下降趨勢最大，60~80 ℃溫度區間下降趨勢次之，80~120 ℃溫度區間下降趨勢平緩。由Young方程可得cos=(2?12)/1，代入上述關系，即溫度升高，接觸角減小；除此外，不同溫度區間內，DBTL對CBT500初期誘導率不同，從而導致不同溫度區間內靜態接觸角、界面張力下降趨勢不一致。

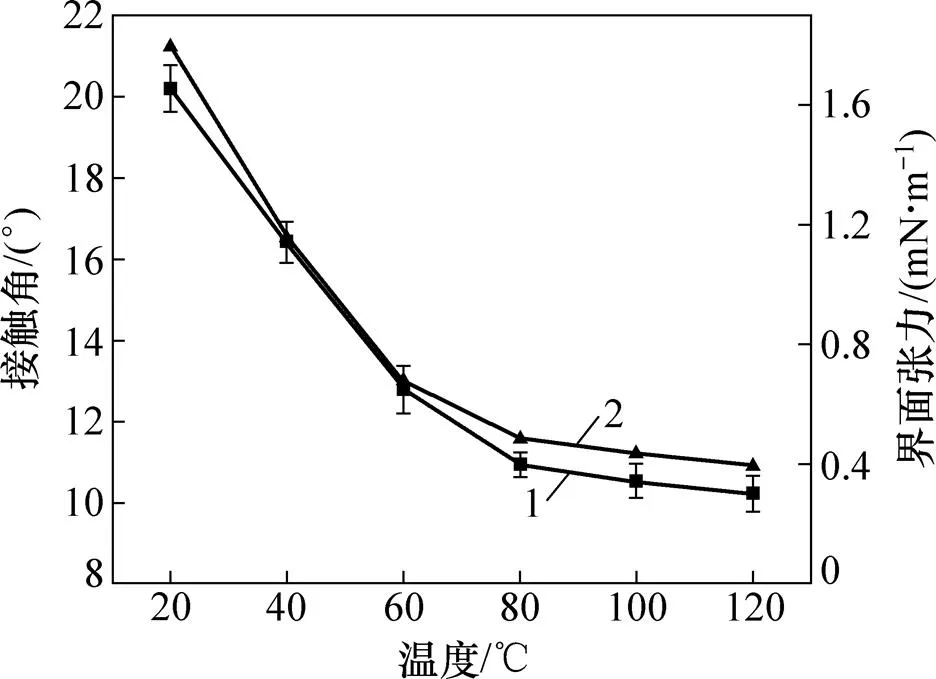
1—接觸角；2—界面張力。

在20~120 ℃溫度范圍內，DBTL在CBT500光滑薄板上最大靜態接觸角為20.202°，低于采用接觸角法獲得高精度界面張力的最小靜態接觸角35°。采用接觸角法計算CBT500與DBTL界面張力誤差大，需要對計算結果進行修正。

3.3 依據相似理論修正接觸角法計算界面張力

相似理論在工程[18]、儀器校正[19]等方面有著廣泛的應用，該應用的基礎是結果趨勢一致，即定性。設原型(調和平均法)與模型(接觸角法)計算條件相似系數為1，結果比為，依據相似理論，采用調和平均法修正接觸角法界面張力計算值，使修正后接觸角法界面張力與調和平均計算值結果比為1。

3.3.1 結果比

根據相似理論，相似系數為1時，不同溫度下結果比滿足式(10)，因此，只需計算一個溫度下結果比即可。采用調和平均法計算20 ℃溫度下CBT500與DBTL界面張力，獲得20 ℃溫度下結果比20，進而獲得不同溫度下結果比。

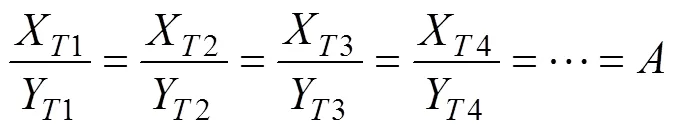
調和平均法計算CBT500與DBTL界面張力(12)，CBT500、DBTL表面張力()、極性分量(p)、色散分量(d)研究是基礎。CBT500色散分量、極性分量通過引入2種測試液體求解二元二次方程組，DBTL色散分量、極性分量通過研究DBTL在PP薄板上靜態接觸角并結合表面張力是材料極性分量、色散分量之和進行二元二次方程組求解。

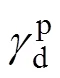
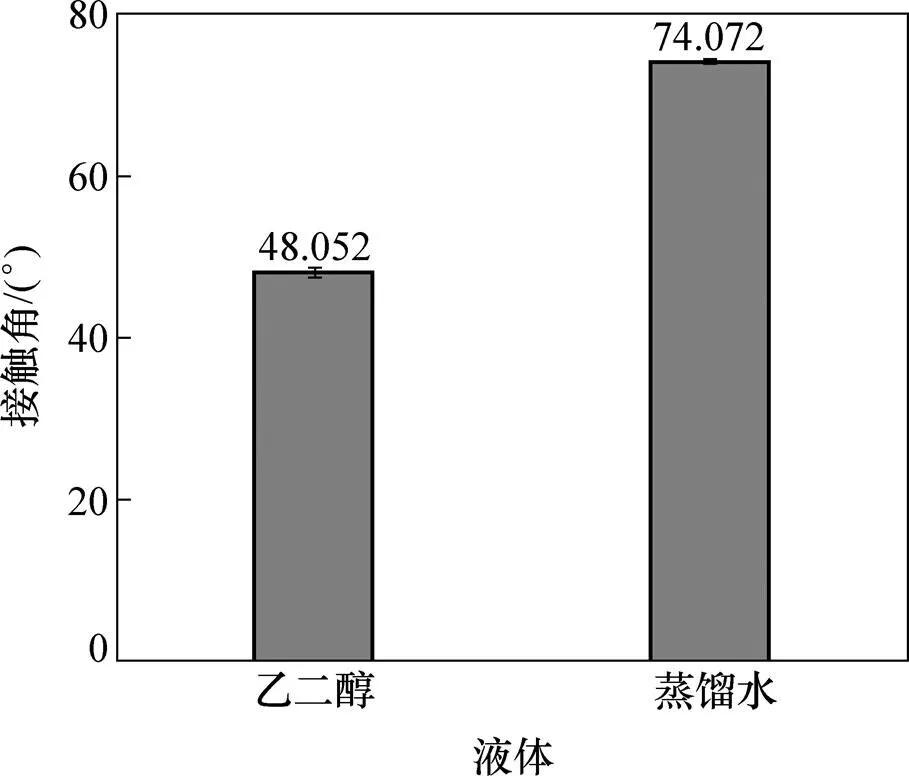
圖5 20 ℃時不同液體在CBT500薄板上靜態接觸角

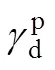
表2 乙二醇和蒸餾水的γd，和[20]

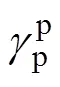
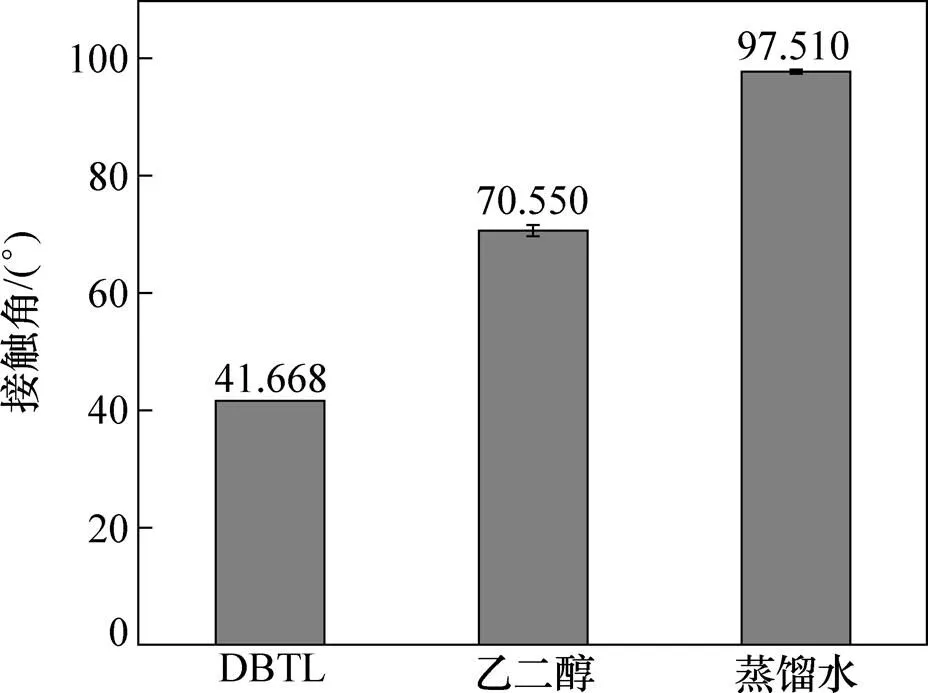
圖6 20 ℃時不同液體在PP薄板上靜態接觸角

根據上述計算，20 ℃溫度下，接觸角法計算CBT500與DBTL界面張力為1.799 7 mN/m，調和平均法計算值為1.2434 mN/m。調和平均法計算值比接觸角法小44.7%，20 ℃溫度下結果比20約為1.447，即=1.477。

3.3.2 修正值

已知結果比為1.447，由式(10)可知，修正后20，40，60，80，100和120 ℃溫度下接觸角法界面張力修正前后結果如圖7所示。由圖7可知：修正前后界面張力與溫度變化規律具有一致性，100 ℃溫度以后界面張力變化細微，修正后接觸角法界面張力比修正前整體下降44.7%，更加接近真實值。

3.4 界面張力與溫度表達式

ANASTASIADIS等[21]認為無污染、無反應條件下，溫度對不同材料體系界面張力的影響呈線性關系。本文忽略混合時物質反應與雜質對界面張力的影響，以斜率變化為分界點，采用最小二乘法分段線性擬合修正后界面張力數據，獲得20~120 ℃溫度范圍內修正后CBT500/DBTL界面張力與溫度函數關系式。依據界面張力與溫度斜率逐漸減小且趨于平緩和界面張力與溫度呈線性關系，以第三段界面張力與溫度關系式作為120~200 ℃溫度范圍內界面張力函數關系式，即20~200 ℃溫度范圍內，修正后CBT500/DBTL的界面張力與溫度之間的分段函數關系式為

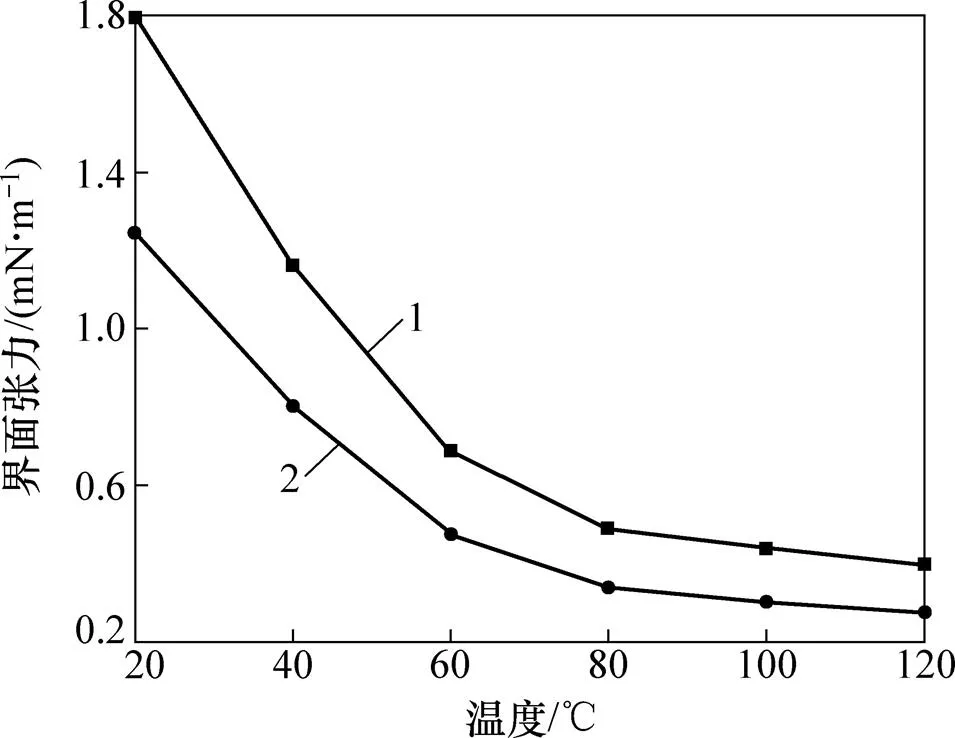
1—接觸角法；2—修正。

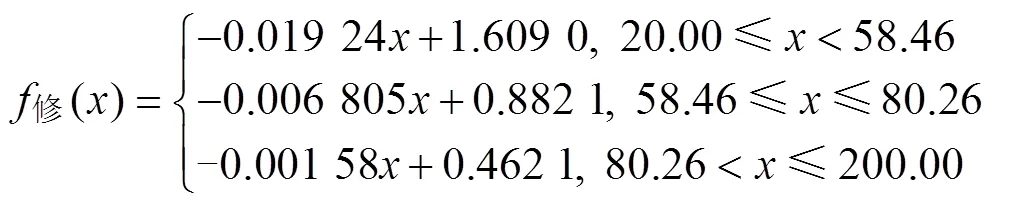
4 結論

1) 在20~120 ℃下：DBTL的表面張力隨溫度升高而減小，呈現出明顯的線性關系。

2) 在20~120℃范圍內，DBTL在CBT500薄板上的靜態接觸角和CBT500/DBTL樹脂體系的界面張力均隨著溫度的升高而減小。不同溫度區間內，二者的減小趨勢不同：在20~60 ℃范圍內，接觸角和界面張力隨溫度升高，下降趨勢最大；在60~80 ℃范圍內，下降趨勢次之；在80~120 ℃范圍內，下降趨勢平緩。

3) 20 ℃下，采用調和平均法計算DBTL與CBT500界面張力為1.243 4 mN/m，接觸角法計算值為1.799 7 mN/m，調和平均法計算值相比接觸角法計算值約小44.74%，結果比=20≈1.447 4；依據相似理論，在20，40，60，80，100和120 ℃溫度下，修正后接觸角法計算得到的DBTL與CBT500界面張力比修正前整體小44.7%，更加接近真實值。

4) 采用最小二乘法分段線性擬合界面張力修正值，得到了20~200 ℃范圍內，CBT500/DBTL體系界面張力與溫度的分段關系式。分別是：20.00~58.46 ℃溫度范圍內，斜率為?0.019 24，截距為1.609；58.46~80.26 ℃溫度范圍內，斜率為?0.006 805，截距0.882 1；80.26~200.00 ℃溫度范圍內，斜率為?0.001 58，截距0.462 1。

[1] PICHETA S. In-situ injection molding: Fully automated from textile to the composite[C]//Aachen Dresden International Textile Conference. Dresden, 2012: 1?4.

[2] WU Wangqing, XIE Lei, JIANG Bingyan, et al. Influence of textile preforming binder on the thermal and rheological properties of the catalyzed cyclic butylene terephthalate oligomers[J]. Composites Part B: Engineering, 2013, 55: 453?462.

[3] ABT T, SáNCHEZSOTO M. A review of the recent advances in cyclic butylene terephthalate technology and its composites[J]. Critical Reviews in Solid State & Material Sciences, 2016, 42(3): 173?217.

[4] YAN Chun, LIU Ling, ZHU Yingdan, et al. Properties of polymerized cyclic butylene terephthalate and its composites via ring-opening polymerization[J]. Journal of Thermoplastic Composite Materials, 2017, 31(2): 1?21.

[5] 何宏, 龍柱, 戴磊, 等. 納米SiO2/聚己內酯(PCL)/聚丁二酸丁二醇酯?聚己二酸丁二醇酯共聚物(PBSA)復合材料的力學及流變性能[J]. 中南大學學報(自然科學版), 2014, 45(2): 383?388. HE Hong, LONG Zhu, DAI Lei, et al. Mechanical and rheological properties of nanoSiO2/PCL/PBSA blends[J]. Journal of Central South University (Science and Technology), 2014, 45(2): 383?388.

[6] JEGAT C, VIRGILIO N, FAVIS B D. Self-assembly of oil microdroplets at the interface in co-continuous polymer blends[J]. European Polymer Journal, 2017, 93: 259?271.

[7] HALáSZ I, BáRáNY T. Phase morphology and mechanical properties of cyclic butylene terephthalate oligomer-containing rubbers: effect of mixing temperature[J]. Materials, 2016, 9(9): 722?733.

[8] 朱定一, 戴品強, 羅曉斌, 等. 潤濕性表征體系及液固界面張力計算的新方法(Ⅱ)[J]. 科學技術與工程, 2007, 7(13): 3063?3069. ZHU Dingyi, DAI Pingqiang, LUO Xiaobing, et al. Novel characterization of wetting properties and the calculation of liquid-solid interface tension(Ⅱ)[J]. Science Technology & Engineering, 2007, 7(13): 3063?3069.

[9] FOWKES F M. Attractive forces at interfaces[J]. Industrial & Engineering Chemistry, 1964, 56(12): 40?52.

[10] LEE B B, RAVINDRA P, CHAN E S. New drop weight analysis for surface tension determination of liquids[J]. Colloids and Surfaces A Physicochemical and Engineering Aspects, 2009, 332(2): 112?120.

[11] BERRY J D, NEESON M J, DAGASTINE R R, et al. Measurement of surface and interfacial tension using pendant drop tensiometry[J]. Journal of Colloid & Interface Science, 2015, 454: 226?237.

[12] WU Souheng. Calculation of interfacial tension in polymer systems[J]. Journal of Polymer Science Polymer Symposia, 1971, 34(1): 19?30.

[13] ZDZIENNICKA A, KRAWCZYK J, SZYMCZYK K, et al. Components and parameters of liquids and some polymers surface tension at different temperature[J]. Colloids and Surfaces A Physicochemical and Engineering Aspects, 2017, 529: 864?875.

[14] SINAYOBYE E, MENSAH-BROWN H, YAYA A, et al. Calculation of interfacial tensions between macromolecular solutions and Soltrol-130 from contact angles measurements[J]. Journal of Engineering & Applied Sciences, 2013, 8(2): 99?104.

[15] 李鐵才, 李西峙. 相似性和相似原理[M]. 哈爾濱: 哈爾濱工業大學出版社, 2014: 1?195.LI Tiecai, LI Xizhi. Resemblance and principles of similarity[M]. Harbin: Harbin Institute of Technology Press, 2014: 1?195.

[16] TONG Xuan, WANG Zhirong, ZHOU Chao, et al. A modeling method for predicting the concentration of indoor carbon dioxide leakage and dispersion based on similarity theory[J]. Energy & Buildings, 2017, 151: 585?591.

[17] YUAN Y, LEE T R. Contact angle and wetting properties[M]. Berlin Heidelberg: Springer, 2013: 3?34.

[18] QING Chun, WU Xiaoqing, HUANG Honghua, et al. Estimating the surface layer refractive index structure constant over snow and sea ice using Monin?Obukhov similarity theory with a mesoscale atmospheric model[J]. Optics Express, 2016, 24(18): 20424?20436.

[19] SHENK J S, SHENK J W, BROWN B, et al. Method and system for increasing optical instrument calibration and prediction accuracy within and across different optical instrument platforms: US, US8548764[P]. 2013?10?01.

[20] 陳曉磊. 固體聚合物表面接觸角的測量及表面能研究[D]. 長沙: 中南大學化學化工學院, 2012: 44?46. CHEN Xiaolei. Surface free energy and contact angle measurement of sold polymer[D]. Changsha: Central South University. School of Chemistry and Chemical Engineering, 2012: 44?46.

[21] ANASTASIADIS S H, GANCARZ I, KOBERSTEIN J T. Interfacial tension of immiscible polymer blends: temperature and molecular weight dependence[J]. Macromolecules, 1988, 21(21): 2980?2987.

(編輯 楊幼平)

Characterization of interfacial tension of CBT500/DBTL as a new low-molecular thermoplastic resin matrix system

FU Jixian1, 2, WU Wangqing1, 2, LIU Yi1, 2, JIANG Bingyan1, 2

(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China; 2. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China)

In order to obtain the real and reliable interfacial tension of a new low molecular mass thermoplastic resin system CBT500/DBTL, a new method based on the harmonic mean method corrected contact angle method was proposed to study the resin mixing mechanism and to guide the development of mixing device. Interfacial tension characterizations were conducted in the range of 20?120 ℃ for the CBT500/DBTL resin matrix system. The least squares method was used to linearly fit the corrected interfacial tension. The results show that the interfacial tension of the resin system decreases with the increase of temperature in the range of 20?120℃, and the corrected interfacial tension obtained by the harmonic mean method is 44.7% lower than that of the contact angle method and closer to true value. The piecewise function of the interfacial tension of the CBT500/DBTL resin system and temperature ranging from 20 to 200℃ is obtained.

in-situ polymerization injection molding; interfacial tension; harmonic mean method; contact angle method; similarity theory

10.11817/j.issn.1672?7207.2018.10.008

TQ320.66

A

1672?7207(2018)10?2423?07

2017?10?22；

2017?12?28

國家自然科學基金資助項目(51405519)；中南大學研究生自主探索創新項目(2017zzts399)(Project(51405519) supported by the National Natural Science Foundation of China; Project(2017zzts399) supported by Graduate Students to Explore Innovative Projects of Central South University)

吳旺青，博士，副教授，從事連續纖維增強熱塑性復合材料先進成型技術研究；E-mail：csuwwq@csu.edu.cn