非均質地基中V?T聯合受荷樁承載力分析

鄒新軍，夏尉桓，王亞雄

?

非均質地基中?聯合受荷樁承載力分析

鄒新軍，夏尉桓，王亞雄

(湖南大學 土木工程學院，湖南 長沙，410082)

為研究非均質地基中單樁基礎在樁頂豎向力()和扭矩()聯合作用下的承載特性，假定樁側地基土剪切模量和極限側摩阻力沿深度呈指數函數非線性增加，并考慮樁?土接觸面上位移的非協調性，根據剪切位移法和樁身荷載傳遞函數建立樁身位移控制方程，引入相應的力和位移邊界條件，導出樁周土體處于理想彈性和塑性受力狀態時的樁身內力位移解答，由此求得不同樁頂載荷工況(不同?組合與加載順序)下的樁身承載力及其包絡線。在此基礎上，進一步采用ABAQUS對?聯合受荷樁進行數值模擬對比分析，獲得不同工況下的樁身破壞機理、影響樁身承載力的關鍵因素及其規律。研究結果表明：樁身承載力隨樁身長徑比的增大而增大，但隨樁土剛度比的增大而逐漸減小；樁頂可承受的豎向力(扭矩)隨扭矩(豎向力)增加不斷減小而趨于零。

樁基礎；?聯合荷載；非均質地基；荷載傳遞函數；數值分析

隨著我國基礎設施建設的不斷推進特別是近海資源的持續性開發，城市立體交通的彎梁橋、跨海大橋、海上風力發電塔等結構物不斷興建。為滿足上部結構對基礎的承載力、變形及穩定性等方面的要求，這類結構物多采用樁基礎，但由于其所處環境復雜，除承受豎向力()、水平力()和彎矩()外，還可能承受不可忽視的扭矩()作用。常規設計方法難以考慮這種復雜受荷工況，不能合理地評價樁身極限承載力，導致設計偏于不安全，因此，對于這類復雜受力環境中的樁基礎設計，應考慮，，或的聯合作用。已有研究者對?[1]，?[2]和??等組合進行了研究，但很少考慮扭矩的共同作用。鑒于問題的復雜性，本文先探討?聯合受荷樁的承載特性。人們對單一豎向受荷樁的承載變形分析進行了系統研究，如：GUO[3]考慮樁?土接觸面位移非協調并視樁周土為Gibson地基，采用荷載傳遞法和剪切位移法得到樁身內力位移解析解；RAJAPAKSE[4]假定樁周土體剪切模量隨深度呈線性變化，使用積分變換法推導出樁基的彈性理論解。目前，一些學者對純受扭樁進行了研究，如：RAJAPKSE[5]引入變分法將樁和土分解為柱形桿件及單獨的彈性土體，并使用Green函數表示應力和位移的關系，然后采用Hankel積分變換求得其數值解；陳勝立等[6]基于傳遞矩陣法和積分變換導出了成層地基的位移解，并根據樁?土位移協調條件導出樁身受扭問題的半解析解；孔令剛等[7]建立了群樁扭轉非線性分析模型，用Mindlin解模擬樁?土相互作用，引入經驗性耦合系數，分析了樁側地基土抗力對樁身扭轉承載力的影響；鄒新軍等[8?9]視樁周土剪切模量隨深度分別呈指數和冪函數分布，并考慮單層和雙層地基，導出樁側土分別處于不同受力狀態時樁頂的扭矩?扭轉角解析解。目前，人們對于?聯合荷載樁的承載變形特性的研究較少。GEORGIADIS等[10?11]將樁身視為彈性桿，以相互作用的非線性軸向彈簧與扭轉彈簧模擬樁周土的約束作用，采用傳遞矩陣法編制出相應計算程序，該法模型簡單，但計算復雜，且不能考慮樁?土接觸面位移非協調性。鄒新軍等[12]視樁周土為Gibson地基，考慮了豎向力和扭矩不同大小組合與加載順序，并考慮樁?土接觸面上位移的非協調性，導出了樁周土分別處于彈、塑性狀態時的樁身內力位移解答。綜上所述，有關?聯合荷載樁的承載特性研究仍有待深入。為此，本文作者基于已有研究成果，以剪切模量隨深度呈指數函數增加來模擬地基的非均質特性，考慮樁?土接觸面上的位移非協調和?不同組合與加載順序等因素，基于剪切位移法和荷載傳遞函數建立樁身位移控制方程，進而推導樁身內力位移解答。在此基礎上，基于ABAQUS進行數值模擬對比分析，進一步探討?聯合受荷樁的破壞機理及其承載力的關鍵影響參數與規律。

1 豎向受荷樁與受扭樁分析

鑒于問題的復雜性，為簡化分析，進行如下假定。

1) 視樁身為理想彈性體，樁周土為非均質地基，即假定樁側地基土剪切模量和樁側極限摩阻力f隨深度均按下式呈指數函數模式增加(見圖1)：

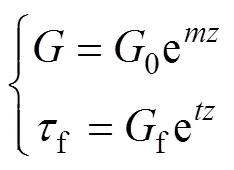
式中：為深度(m)；0和f分別為樁側土體剪切模量(MPa)和極限摩阻力的分布常數(MPa)；和為非線性系數(m?1)，=/；為土層厚度(m)；為非負的量綱一常數，取決于上覆土層的特性(可由試驗確定)，=0時表示土層為均質土。的取值與的取值相同。

2) 樁周土處于彈性受力階段時樁?土位移協調，進入塑性階段后樁?土接觸面可局部相對滑移。

3) 任一深度處的樁側摩阻力服從理想彈塑性模型，即該深度處的摩阻力線性增加至極限摩阻力后保持不變，且該極限值隨深度按式(1)變化。

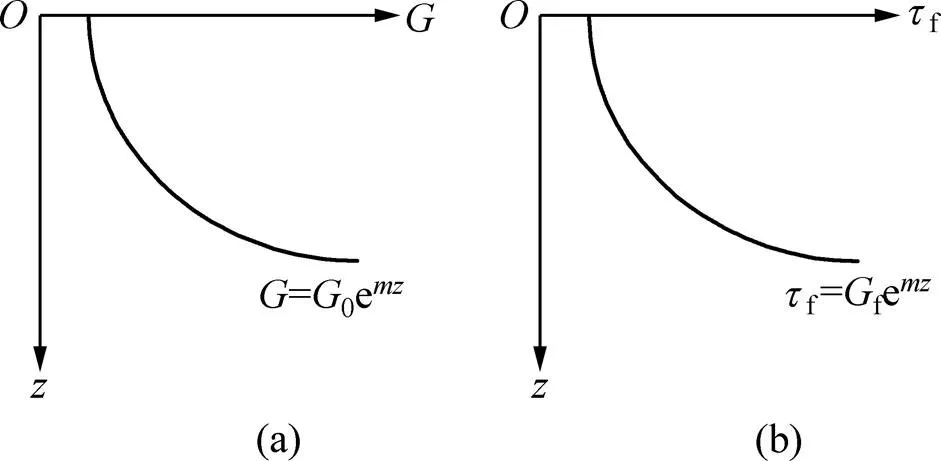
(a) 剪切模量分布模型；(b) 極限摩阻力分布模型

1.1 非均質地基中豎向受荷樁分析

當樁頂僅作用豎向力且樁周土處于彈性受力狀態時，由樁身微元體的力平衡條件等可建立樁身位移控制方程：

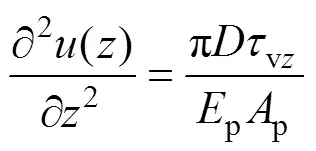
式中：vz為樁側摩阻力(kPa)；p和p分別為樁身的截面積(m2)和材料彈性模量(kPa)；為樁徑(m)；()為深度處的樁身截面位移(m)。

引入RANDOLPH等[13]導出的樁?土接觸面上的摩阻力與位移間的關系式：

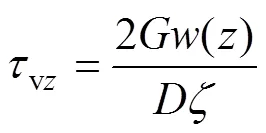
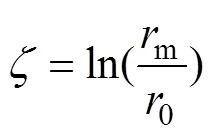
式中：0為樁身半徑(m)；m為影響半徑(m)，m=2.5(1?)；為土體泊松比，為樁長(m)；為/2深度處與樁底處土的剪切模量之比；()為樁?土接觸面上土體的豎向位移(m)；為軸向荷載傳遞因 子[13]。

考慮樁?土位移協調即()=()，將式(1)，(3)及(4)代入式(2)可得

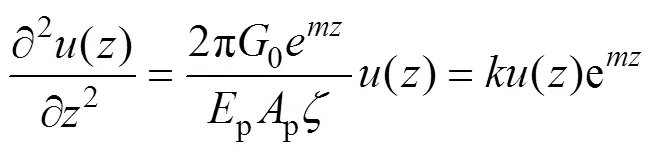
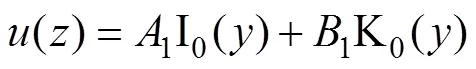
樁身截面上的軸力與位移關系式如下：

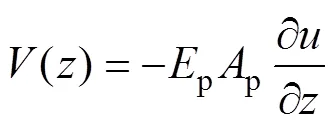
將式(6)代入式(7)可得

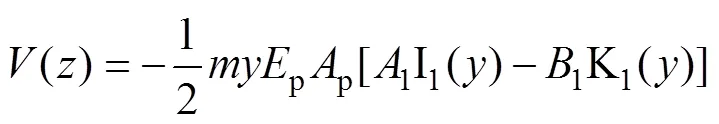
式中：I1(?)和K1(?)分別為第一類和第二類變型Bessel函數。

分別用b與b表示樁底處的軸力和位移，并引入樁底處力與位移的邊界條件：

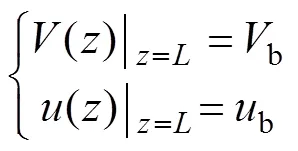
再引入Randolph和Wroth關于樁底處b與b-的關系式[14]：

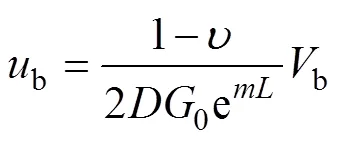
聯立式(6)，(8)和(10)，解得待定系數1和1：

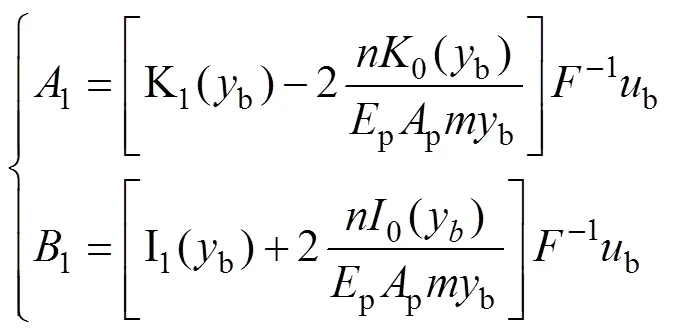
將式(11)分別代入式(6)和(8)可得

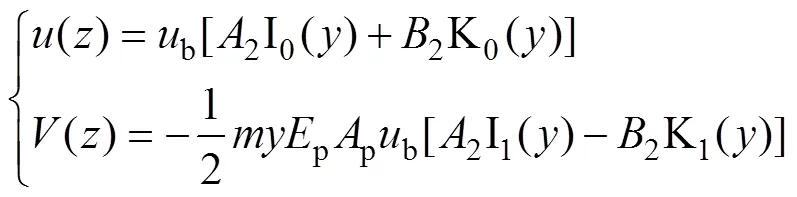
其中：21b；B=B1b。

不斷增加樁頂豎向力，直至出現樁?土相對滑移后，假定達到t時樁?土相對滑移點已發展至深度v1處。為求解此時的樁頂豎向位移t和v1處樁身軸力e及位移e，取樁頂至v1處的樁段為研究對象，由豎向位移連續與力平衡條件可得樁頂豎向力t及位移t：

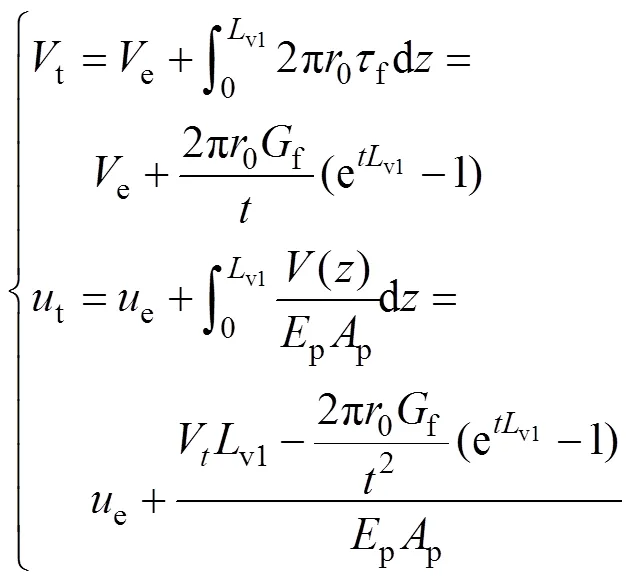
v1處樁土位移協調即e=e，聯立式(1)和(3)得

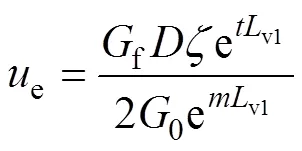
由式(12)可得v1處樁身軸力為

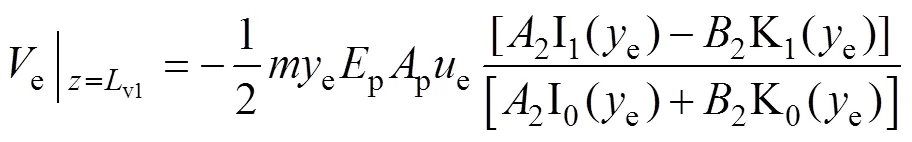
1.2 非均質地基中受扭樁分析

樁頂僅作用扭矩且樁周土處于彈性狀態時，由樁身微元體力平衡條件等可建立樁身扭轉控制方程：

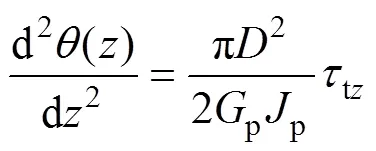
式中：()與tz分別為深度處樁身的扭轉角 (rad)和環向切應力(kPa)；pp為樁身抗扭剛度(kN·m2)。

引入純受扭樁樁?土接觸面上的土體環向切應力tz與轉角的關系式：

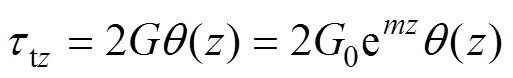
則式(16)可變為

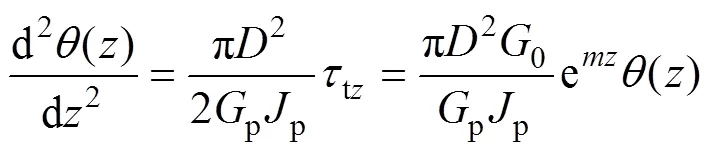
由參數變換將式(18)轉為修正Bessel函數后可得

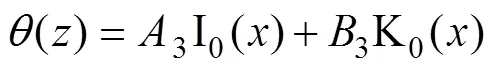
樁身任意截面處的扭矩與扭轉角存在如下關系：

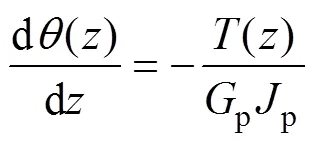
式中：()為深度為處樁身扭矩(kN·m)。

將式(19)代入式(20)后得()表達式：

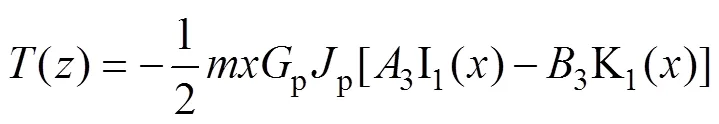
而樁底處的扭轉邊界條件為

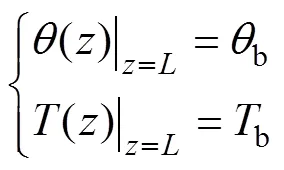
式中：b與b分別為樁底截面的扭矩和扭轉角，

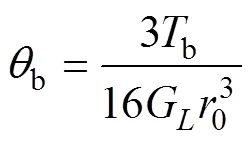
其中：G為樁底處土體的剪切模量(kPa)。聯立式(19)，(21)和(23)可得

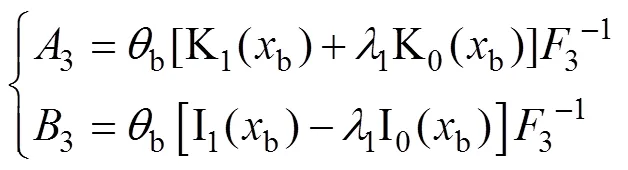
將式(24)分別代入式(19)和(21)可得

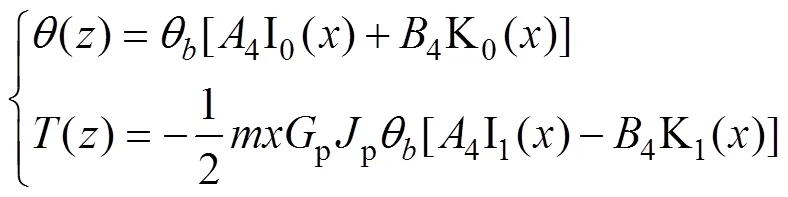
其中：43b；43b。

不斷增大樁頂扭矩，直至出現樁?土相對滑移為止。假定達t時樁?土相對滑移開展至某一深度t1處，為求解此時的樁頂扭轉角t及t1處的樁身扭矩e與扭轉角e，以樁頂至t1處樁段為研究對象，由力平衡與扭轉位移連續條件可得

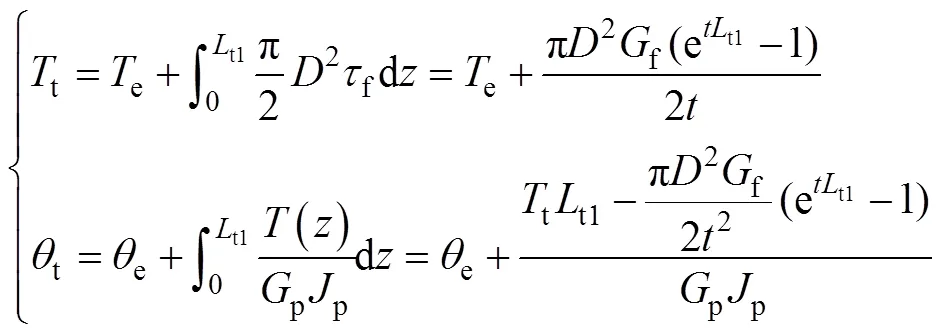
聯立式(1)和(17)可得

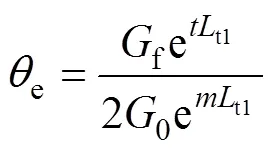
由式(25)可求得t1處的樁身扭矩為

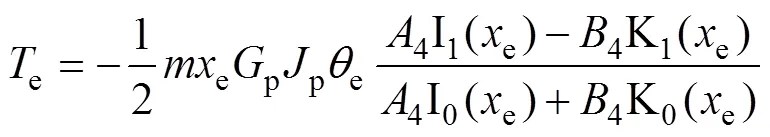
2 不同加載順序下V?T受荷樁分析

在樁頂?聯合作用下，假定深度處樁周土體對樁身的剪切力τ可分解為豎向側摩阻力vz與環向切應力tz(如圖2所示)，且滿足

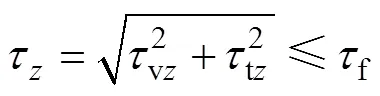
2.1 彈性→彈塑性階段

當樁頂先作用豎向力t(或扭矩t)且樁側地基土尚處于彈性階段時，再施加t(或t)。當t(或t)很小時，土體仍處于彈性狀態，可分別按式(12)和式(25)求解樁身內力(軸力、扭矩)及變形(位移、轉角)；隨t(或t)增加(如圖3所示)，地基土開始進入塑性階段，假定樁?土臨界滑移點距樁頂v3(或t3)，并將將該截面的內力與位移分別記為e(或e)和e(或e)。

當加載順序為時，根據式(29)及前述解答可求得樁側土體剪切應力為

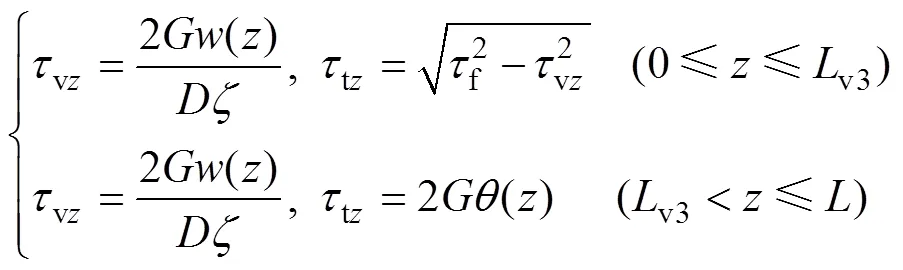
取樁頂至v3處的樁段為分析對象，根據平衡原理與位移協調條件，可求得樁頂扭矩t為

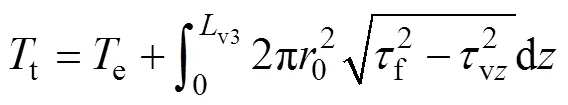
當加載順序變為時，樁側土體剪切應力為

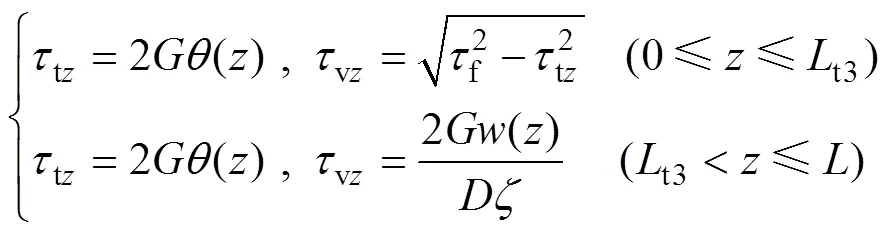
同理，取樁頂至t3處的樁段為分析對象，可求得樁頂的豎向力t為

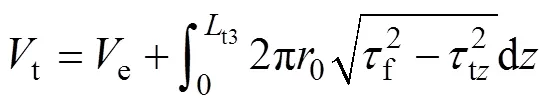
從彈性到彈塑性階段，無論是加載還是加載，隨著2種荷載組合(t，t)的增加，臨界滑動點由地表逐漸發展到樁底，樁周土體由部分進入塑性到全部進入塑性，此時對應的t(t)即為樁在承受一定豎向力t(扭矩t)下所能承受的極限扭矩(豎向力)，不同的(t,t)即構成承載力包絡線。

2.2 彈塑性→彈塑性階段

當加載順序為，樁頂作用較大豎向力t且樁周土已部分處于塑性狀態(相應樁?土臨界滑移點距樁頂v1)時，再施加扭矩t，則臨界滑移點將從v1繼續向下發展至v2處(見圖4)，該截面扭矩與扭轉角仍表示為e和e。

由式(28)及前述解答可求得樁側土體剪切應力：

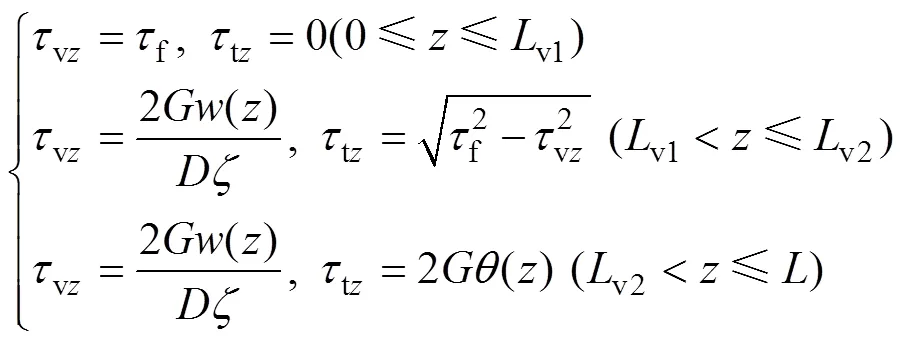
取樁頂至v2處的樁段為分析對象，根據力平衡與位移協調條件，可求得樁頂扭矩t：

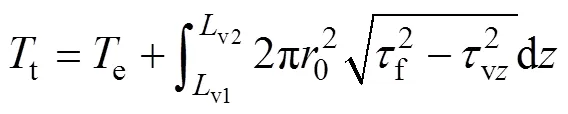
當加載順序變為時，樁頂受到較大扭矩t且樁周土已部分處于塑性狀態(相應樁?土臨界滑移點距樁頂t1)后，再施加豎向力t，則臨界滑移點從t1繼續向下發展至t2處(見圖4)，該截面豎向力與沉降表示為e和e。同理可求得樁側土體剪切應力為

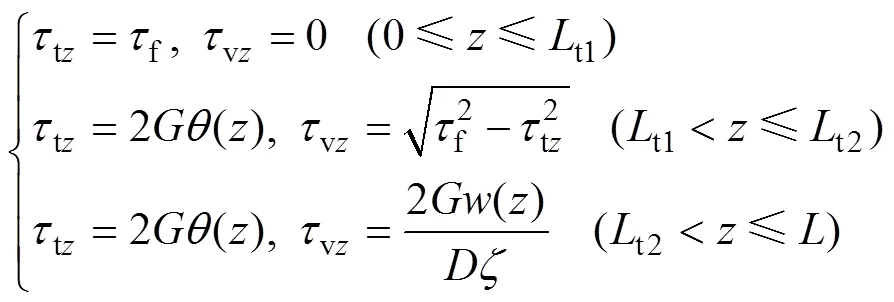
取樁頂至t2處的樁段為分析對象，根據力平衡與位移協調條件，可求得樁頂豎向力：

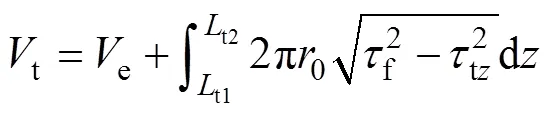
同樣，從彈塑性到彈塑性階段，對和這2種加載順序，隨著2種荷載組合(t，t)的增加，臨界滑動點由v1(t1)處發展至樁底，樁周土全處于塑性階段，此時，對應的t(t)即為樁在承受一定豎向力t(扭矩t)下所能承受的極限扭矩(豎向力)，不同(t，t)即可構成承載力包絡線。

3 方法驗證與參數分析

3.1 方法驗證

為驗證上述解答，利用文獻[15]和[16]中的模型試驗結果驗證單一豎向受荷樁與純受扭樁解答；在此基礎上，再與文獻[11]和[12]中給出的?聯合受荷樁試驗結果與理論結果進行對比。

對于單一豎向受荷樁，計算參數取值如表1所示。

表1 豎向受荷樁計算參數

文獻[15]中模型樁豎向承載力為0.338 MN，本文計算值為0.314 MN，相對誤差為7.1%。

對于純受扭樁，取文獻[16]中的2根模型樁扭轉試驗結果進行對比。計算參數按文獻[17]中方法確定，其中，樁身抗扭剛度為12.8 MN?m2，和分別取 2.00 m?1和0.25 m?1，其余主要參數見表2。

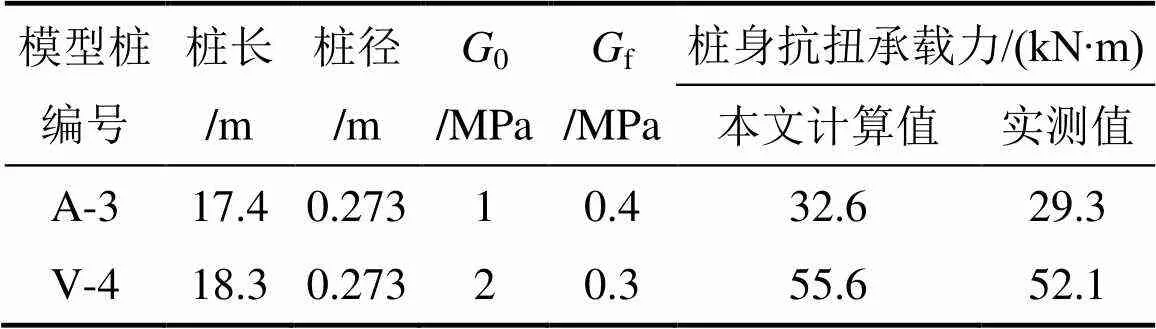
表2 純受扭樁計算參數與結果

由表2可知：由本文解答求得的樁身扭矩承載力均略高于模型試驗值。其原因主要在于假定的式(1)模型難以完全符合文獻[16]中模型樁的樁周土質條件，此外，一些其他復雜試驗條件也不能予以考慮。

對于?聯合受荷樁，將本文計算結果與文獻[11]中的試驗結果、理論結果以及文獻[12]中的計算值進行對比。采用的樁土參數如表3所示。樁頂先作用扭矩1.5 N?m，后施加豎向力。

表3 V?T聯合受荷樁計算參數

樁頂在承受一定扭矩情況下豎向荷載與沉降的關系曲線見圖5。從圖5可知：按本文方法獲得的荷載位移曲線變化規律與4根模型樁的實測曲線有一定的相似性，由此確定的?聯合受荷樁的豎向承載力約為174.5 N，與文獻[11]中的理論計算值(約186.5 N)相對誤差約為6.4%，與文獻[12]中的計算值(約 165.2 N)相對誤差約為5.6%。文獻[12]假定樁側地基土剪切模量和極限側摩阻力均隨深度線性增加，而本文采用指數函數模型，且本文的計算結果均值略高于文獻[12]中的值。另外，文獻[11]中4根模型樁試驗結果具有一定的離散性，并與其理論計算值有一定差異，相比而言，本文計算結果位于試驗散點最大值與最小值之間，并與文獻[11]中結果更接近。

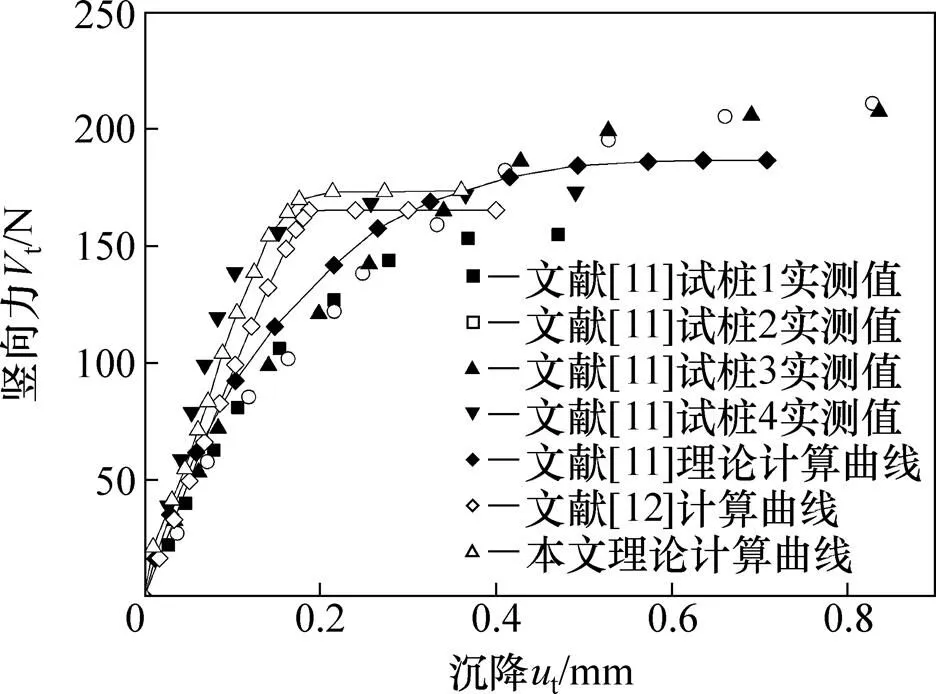
圖5 V?T聯合受荷樁樁頂豎向力?位移對比分析

3.2 參數分析

為了進一步探討影響?聯合受荷樁承載力的關鍵參數與規律，進一步基于ABAQUS進行數值模擬對比分析。

為驗證模型的正確性，與文獻[11]中算例進行對比分析，結果如表4所示。從表4可見：基于ABAQUS的樁身豎向承載力數值分析結果與理論計算值較吻合。

表4 基于ABAQUS的分析模型驗證

在上述可行性驗證的基礎上，進一步對參數進行分析。模型土體計算參數(見表5)如下：彈性模量為5 GPa，泊松比為0.35，剪脹角為0°，內摩擦角為5°。黏聚力由相應深度處的土體抗剪強度反算得到。

模型分析簡圖和基于ABAQUS的有限元網格劃分如圖6所示。

表5 8號試樁計算參數

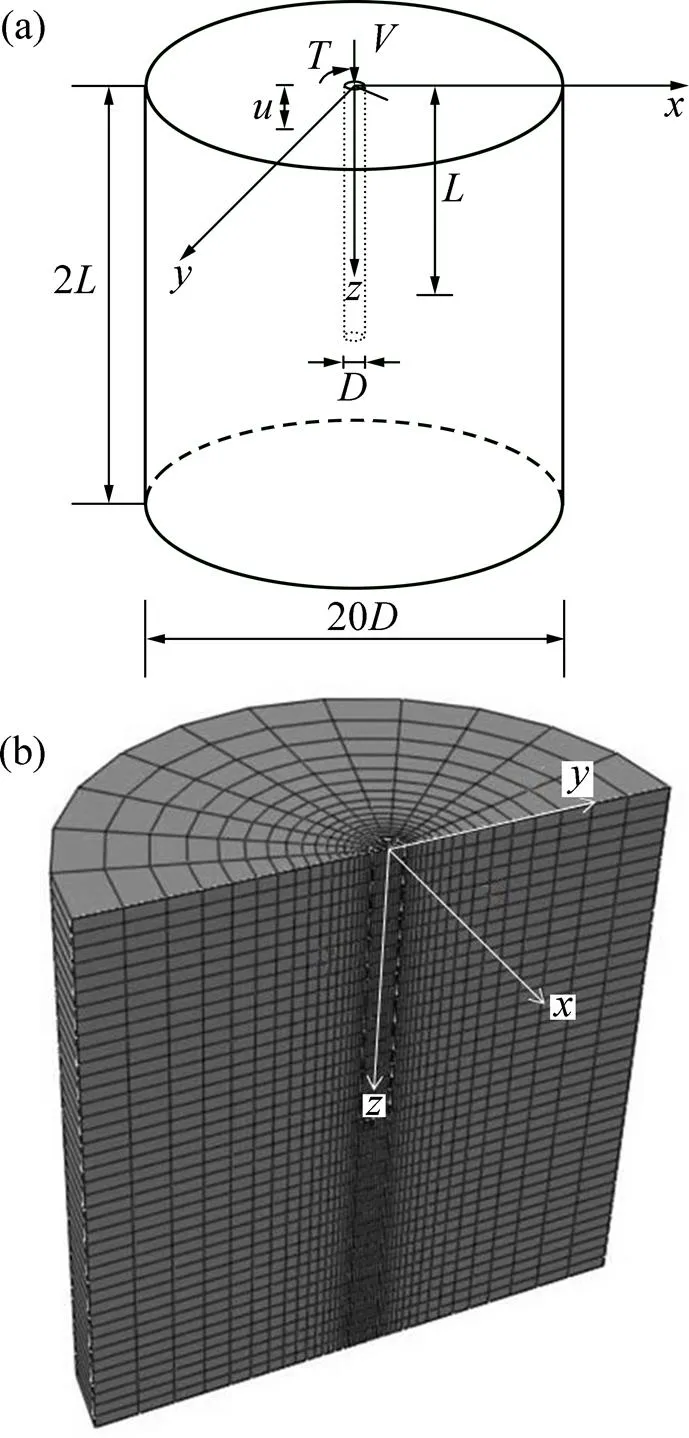
(a) 模型簡圖；(b) 有限元網格

經對比分析，為消除模型邊界效應，模型中土體的直徑為樁徑的20倍，深度為樁長的2倍。樁身視為彈性體，土體破壞服從摩爾庫侖準則。樁?土接觸面采用hard-contact。將樁頂受力面耦合在一起，并選用圓心作為其參考點，荷載施加于該參考點上。模型邊界約束條件如下：兩側約束?平面上的位移，底部約束各個方向的位移。單元類型均為C3D8R，樁身和地基土體單元數量分別為1 800個和18 480個。

取較常見的樁身長徑比在10~50范圍內的5個代表值和不同加載順序進行對比分析，得到相應的樁頂豎向力t與扭矩t，如圖7所示。從圖7可見：隨增大，樁身承載力逐漸增加，承載力包絡線呈現外擴趨勢，且對應的樁身承載力包絡線始終位于加載時包絡線的外側。

為探討樁土剛度比對承載力的影響，采用6組不同獲得其樁頂豎向力與扭矩，相應的樁身承載力包絡線如圖8所示。從圖8可見：隨增加，樁身承載力的包絡線呈收縮趨勢而減小。

為獲得量綱一化承載力包絡線，以樁徑比為10的樁為例，分析得到其最大豎向承載力為1 220 kN，最大承載扭矩為1 104 kN?m。當豎向荷載為1 195.6 kN時，可以得到相應的極限承載扭矩為176.64 kN?m，此時位移比/()=2(其中：為樁頂沉降，為樁頂扭轉角)，將樁頂荷載量綱一化，改變樁頂荷載組合，?聯合荷載下的破壞包絡線如圖9所示。

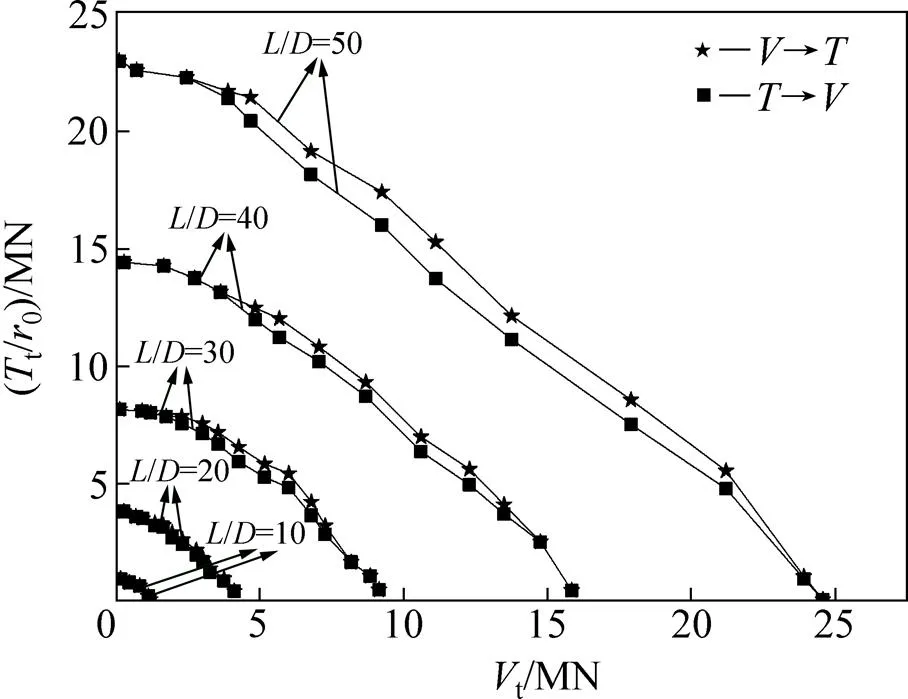
圖7 長徑比L/D和加載順序對樁頂承載力包絡線的影響

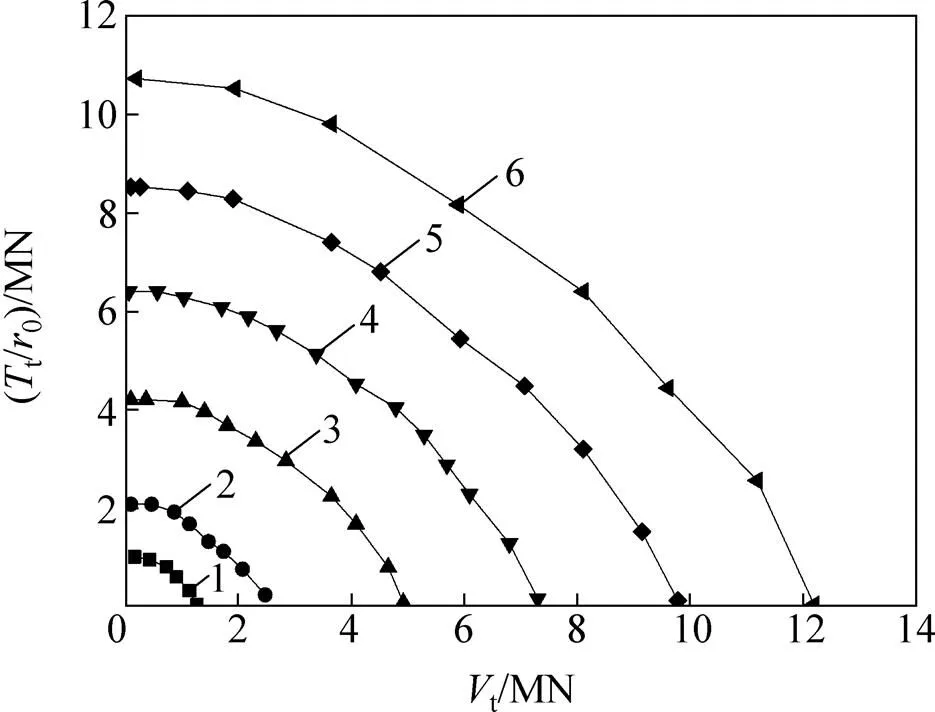
λ：1—5 000；2—2 500；3—1 250；4—850； 5—600；6—500。

圖7~9表明：在上述參數的變化范圍內，對于?聯合受荷樁，隨樁頂扭矩增加，樁頂所能承受的豎向荷載逐漸減小，且減幅呈現先大后小的趨勢，但最終趨于零。

相比于單一受荷樁，?聯合受荷樁的破壞主要由地基土強度破壞引起；同時，隨扭矩荷載增加，樁身破壞模式由單一豎向受荷時的刺入式破壞逐漸轉變為扭轉剪切破壞，此時樁周土應力較大，樁底有一定刺入，樁底土形成滑動面，出現剪切破壞。

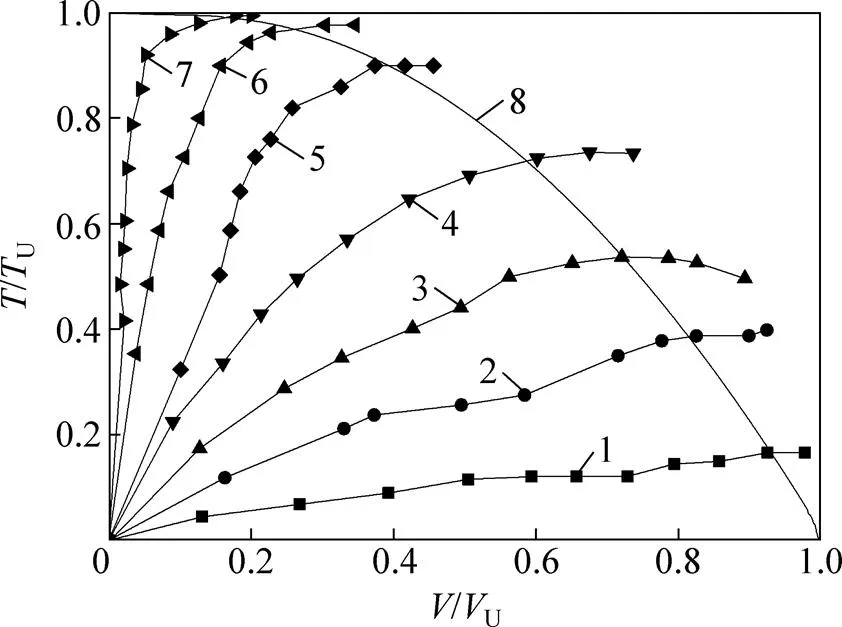
1—u/(Dθ)=2.00；2—u/(Dθ)=1.00；3—u/(Dθ)=0.75； 4—u/(Dθ)=0.50；5—u/(Dθ)=0.30；6—u/(Dθ)=0.25； 7—u/Dθ=0.10；8—包絡線。

4 結論

1) 采用剪切位移法和樁身荷載傳遞函數建立不同?加載順序下的樁身位移控制方程，并引入相應邊界條件后，導出樁側土分別處于彈性或彈塑性時的樁身內力位移解答。

2) 通過與已有理論與模型試驗結果的對比分析，驗證了所給出的單一豎向受荷樁、純受扭樁以及?聯合受荷樁的內力位移解答的合理性。

3) 樁身承載力隨增大而增大，但隨的增大而逐漸減小。

鑒于問題的復雜性，文中的解答及相關結論有待更深入地進行理論研究與試驗驗證。

[1] 鄒新軍, 趙明華, 鄔寶林. 成層地基中傾斜受荷群樁的非線性有限元分析[J]. 中南大學學報(自然科學版), 2006, 37(4): 820?825. ZOU Xinjun, ZHAO Minghua, WU Baolin. Nonlinear finite element analysis of pile group under inclined loads in stratified subgrade[J]. Journal of Central South University(Science and Technology), 2006, 37(4): 820?825.

[2] 陳仁朋, 鄭中, 孔令剛, 等. 水平及扭轉荷載作用下群樁基礎受力分析方法[J]. 巖土工程學報, 2013, 35(8): 1463?1469. CHEN Renpeng, ZHENG Zhong, KONG Linggang, et al. Analysis method for pile groups subjected to lateral and torsional loads[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1463?1469.

[3] GUO Weidong. Vertically loaded single piles in Gibson soil[J]. Journal of Geotechnical Engineering and Geoenvironmental Engineering, ASCE, 2000, 126(2): 189?193.

[4] RAJAPAKSE R K. Response of an axially loaded elastic pile in a Gibson soil[J]. Geotechnique, 1990, 40(2): 237?249.

[5] RAJAPAKSE R. A torsion load transfer problem for a class of non-homogenous elastic solids[J]. International Journal of Solids and Structures, 1988, 24(2): 139?151.

[6] 陳勝立, 張利民. 層狀地基中單樁的扭轉變形分析[J]. 巖土工程學報, 2005, 27(5): 531?534.CHEN Shengli, ZHANG Limin. Torsional response of single pile embedded in layered ground[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(5): 531?535.

[7] 孔令剛, 張利民. 群樁扭轉非線性模型[J]. 巖土力學, 2009, 30(8): 2231?2236. KONG Linggang, ZHANG Limin. Nonlinear analysis of pile groups subjected to torsion[J]. Rock and Soil Mechanics, 2009, 30(8): 2231?2236.

[8] 鄒新軍, 徐洞斌, 王亞雄. 成層地基中單樁受扭彈塑性分析[J]. 湖南大學學報(自然科學版), 2014, 41(9): 72?78.ZOU Xinjun, XU Dongbin, WANG Yaxiong. Elastic-plastic analysis of torsional single pile in layered subsoil[J]. Journal of Hunan University (Natural Sciences), 2014, 41(9): 72?78.

[9] 鄒新軍, 趙靈杰, 徐洞斌, 等. 雙層非均質地基中單樁受扭彈塑性分析[J]. 巖土工程學報, 2016, 38(5): 828?836.ZOU Xinjun, ZHAO Lingjie, XU Dongbin, et al. Elastic-plastic torsional behavior of single pile in double-layered non-homogeneous subsoil[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(5): 828?836.

[10] GEORGIADIS M. Interaction between torsional and axial pile response[J]. Numerical and Analytical Methods in Geomechanics, 1987, 11(6): 645?650.

[11] GEORGIADIS M, SAFLEKOU S. Piles under axial and torsion loads[J]. Computers and Geotechnics, 1990, 9(4): 291?305.

[12] 鄒新軍, 王亞雄, 徐洞斌. 彎梁橋中?聯合受荷樁承載力分析[J]. 中國公路學報, 2015, 28(10): 51?58. ZOU Xinjun, WANG Yaxiong, XU Dongbin. Bearing capacity analysis of?combined loaded piles in curved girder bridges[J]. China Journal of Highway and Transport, 2015, 22(10): 51?58.

[13] RANDOLPH M F, WROTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of Geotechnical Engineering Division, ASCE, 1978, 104(12): 1465?1488.

[14] RANDOLPH M F, WROTH C P. An Analysis of the vertical deformation of pile groups[J]. Geotechnique, 1979, 29(4): 423?439.

[15] 江杰, 黃茂松, 顧倩燕. 非均質地基中群樁豎向荷載沉降關系分析[J]. 巖土力學, 2008, 29(8): 2092?2096. JIANG Jie, HUANG Maosong, GU Qianyan. Analysis of settlements of vertically loaded pile groups in non-homogeneous soil[J]. Rock and Soil Mechanics, 2008, 29(8): 2092?2096.

[16] STOLL U W. Torque shear test of cylindrical friction piles[J]. Civil Engineering, ASCE, 1972, 42(4): 63?64.

[17] GUO Weidong, RANDOLPH M F. Torsional piles in non-homogeneous media[J]. Computers and Geotechnics, 1996, 19(4): 265?2.

(編輯 陳燦華)

Bearing capacity analysis of a single pile under combined?Loads in non-homogeneous subsoil

ZOU Xinjun, XIA Weihuan, WANG Yaxiong

(College of Civil Engineering, Hunan University, Changsha 410082, China)

To discuss the bearing behavior of a single pile under combined loading of vertical forceand torsionin non-homogeneous subsoil, the control equation of the pile shaft was set up by using the pile shaft load transferring function and shear displacement method, in which the exponential function model was adopted to simulate the increasing change of subsoil shear modulus and ultimate side resistance with depth, and the non-coordination deformation along the pile-soil interface was considered as well. Then, force and displacement boundary conditions were introduced to deduce the analytical solutions for the inner forces and deformation of the pile shaft under ideal elastic-plastic bearing stages of subsoil. Based on the obtained solutions, various combined values and loading sequencesofandat the pile top were adopted to determine the bearing capacity of the pile shaft, from which failure envelops were plotted correspondingly. Further numerical analyses were carried out by ABAQUS to find out the failure mechanism and the key factors that affect the bearing capacity of?combined loaded piles. The results show that the bearing capacity of pile shaft increases with the increase of aspect ratio, while decreases with the increase of the ratio of the constant coefficient of the subsoil shear modulus distribution function to that in the stiffness ratio (λ) of pile shaft to subsoil. Increasing the torsion (or the vertical force) at the pile top will decrease the vertical (or torsional) bearing capacity of a final zero value.

pile foundations;?combined loads; non-homogeneous subsoil; load transfer functions; numerical analysis

10.11817/j.issn.1672?7207.2018.10.023

TU473.1

A

1672?7207(2018)10?2553?08

2017?10?12；

2017?12?21

國家自然科學基金資助項目(51578231，51378197)(Projects(51578231, 51378197) supported by the National Natural Science Foundation of China)

鄒新軍，博士，副教授，從事地基基礎與支擋結構研究；E-mail :xjzouhd@hnu.edu.cn