動態失速下H型垂直軸風力機實時變槳控制規律

張立軍，馬東辰，趙昕輝，米玉霞，張松，王旱祥，姜浩

?

動態失速下H型垂直軸風力機實時變槳控制規律

張立軍1，馬東辰1，趙昕輝1，米玉霞1，張松2，王旱祥1，姜浩1

(1. 中國石油大學(華東) 機電工程學院，山東 青島，266580；2. 中國石油大學(華東) 化學工程學院，山東 青島，266580)

針對垂直軸風力機風能利用率低、自啟動能力弱的問題，以1 kW H型垂直軸風力機為研究對象，通過對比美國Sandia國家實驗室動態失速下測得的風力機實驗結果與風洞靜態實驗結果，分析動態失速對槳距角調節的影響規律；以風輪的最大切向力為目標，得到垂直軸風力機在上風區和下風區的最佳理論攻角分別為14.8°和?14.8°。為使風輪在旋轉過程中維持在最佳攻角附近，基于雙致動盤多流管理論進行Matlab編程計算，建立風輪工作狀態下的受力模型，獲得垂直軸風力機在各個方位的槳距角。通過對0°和180°方位角下的槳距角進行修正，給出垂直軸風力機1周變槳距規律。最后，利用雙致動盤多流管理論對提出的變槳控制規律進行理論驗證。研究結果表明：利用該變槳距規律得到的風能利用率可以由34.6%提高到42.8%。

垂直軸風力機；動態失速；槳距角；最佳攻角；雙致動盤多流管

由于能源危機日益嚴重，風能以其綠色、無污染、可再生等特點受到人們的廣泛關注。我國風能資源豐富，根據國家氣象局資料，我國近海70 m高度年平均風功率密度可達300 W/m2以上，大于6 m/s風速的累計時間可達4 000 h。風力發電機根據風輪旋轉軸相對地面的安裝角度分為垂直軸風力發電機(VAWT)和水平軸風力發電機(HAWT)，其中，垂直軸風力發電機以其無需安裝對風裝置、易于安裝和維修等優點，越來越受到人們的關注。然而，現有商業H型垂直軸風力發電機風能利用率僅在30%~35%之間，且存在自啟動能力弱等不足，在很大程度上限制了其規模化發展和應用。在垂直軸風力機旋轉過程中，葉片攻角隨方位角不斷變化，不能維持在最佳攻角處，是其風能利用率低的主要原因[1]。通過改變槳距角以達到調節攻角的目的是改善風力機風能利用率的主要途徑。曹成帥等[2]針對風剪、湍流等影響因素，提出基于系統分解的獨立變槳距控制策略，通過將互不耦合子系統疊加得到變槳距變化規律；廉正光等[3?4]利用雙曲柄調距機構及雙偏心軸機構，設計了一種新型調距機構，并且采用該機構制造出風力發電機樣機；趙振宙等[5]采用擾流技術，通過適當增大0°和180°處擾流角以提高風力機的整體性能；梁云峰等[6]針對變速恒頻風力發電機組的功率控制，設計了一套可以實現快速控制的液壓變槳距系統。上述研究提出的葉片槳距角調節方法在一定程度上可以提高風能利用率，改善風力機啟動性能，但所運用的氣動參數是在靜態失速條件下設定的，未考慮動態失速的影響，而翼型的靜態結果[7]是在風輪固定不動時，通過風洞實驗測得的各個攻角下的升阻力系數, 這不能真實反映風力機的實際工作狀況。垂直軸風力機在正常工作中，葉片攻角隨方位角不斷變化總會發生動態失速[8]。因此，有必要研究動態失速下垂直軸風力機槳距角調節方法，得出動態失速下葉片槳距角隨方位角的變化規律，以提高風能利用效率。

1 動態失速對槳距角調節的影響

動態失速是垂直軸風力發電機在低尖速比下運行時的必然結果[8]，是指在進口來流攻角快速變化的過程中，風輪葉片所表現出的與靜態風洞實驗完全不同的氣動特性[9]。

美國Sandia國家實驗室測試正常工作時的垂直軸風力機，在雷諾數=3.6×105條件下，得到了動態失速時NACA0012翼型的升阻力系數[10]，2組結果對比如圖1和圖2所示。由于NACA翼型為對稱翼型，其升力系數曲線關于原點對稱，阻力系數曲線關于縱軸對稱，故圖1和圖2中僅分別給出了葉片攻角大于0°時的升力系數和阻力系數。

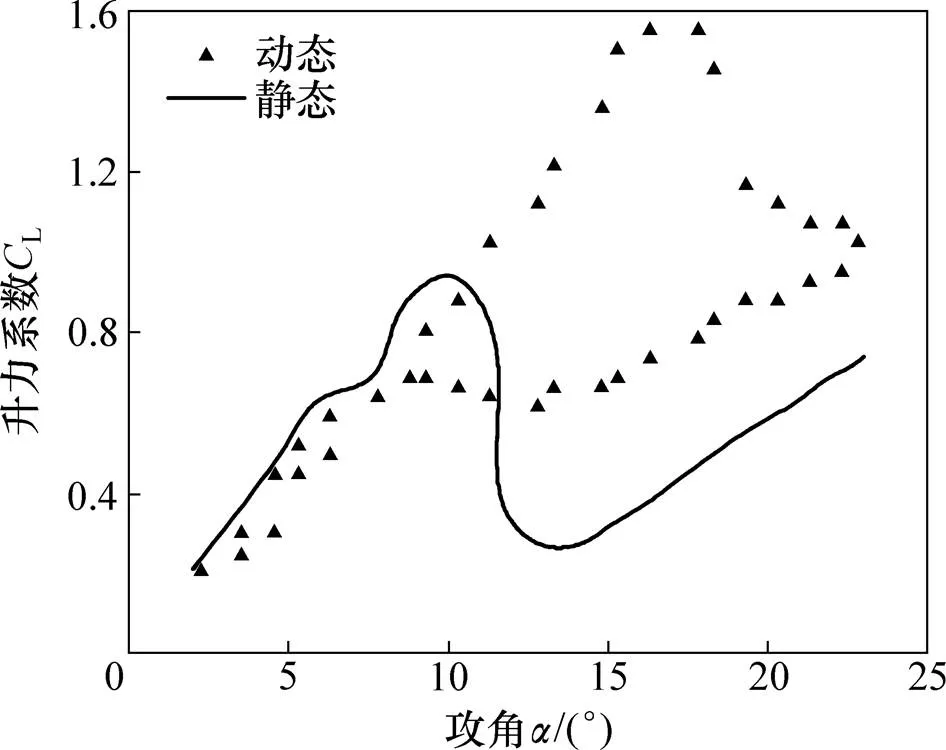
圖1 升力系數對比圖

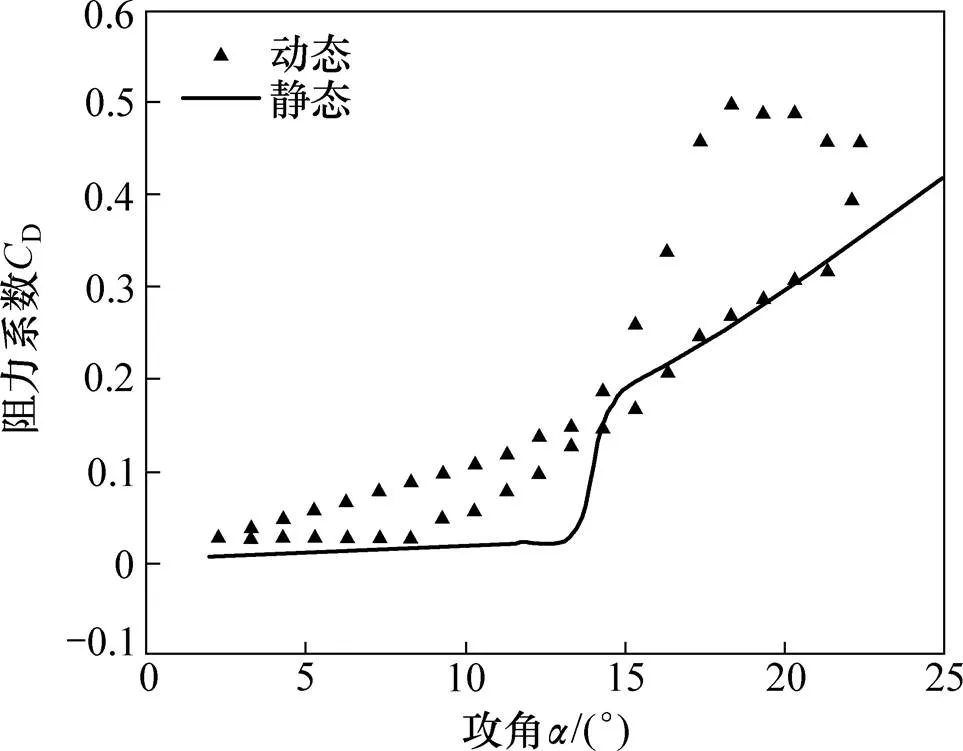
圖2 阻力系數對比圖

從圖1和圖2可知：在靜態條件下，當葉片攻角=10°左右時，升力系數達到最大值。而在動態失速下所測的實驗結果表明：當攻角=17°左右時，升力系數達到最大值，風力機發生失速的攻角出現了延遲。在風力機旋轉過程中，攻角最大值出現在23°左右。此后，攻角逐漸變小，按照靜態風洞實驗結果，在攻角變小過程中，升力系數在各個攻角處的值與攻角變大過程中的值一致。而考慮動態失速影響所測得的實驗結果顯示：在攻角變小過程中，升力系數變化趨勢出現了明顯的滯回現象；在攻角變大和攻角變小過程中，同一個攻角對應的升力系數不同，且在變大過程中升力系數較大。

同樣，從圖2可以看出：垂直軸風輪阻力系數由于受動態失速的影響，也發生了明顯的滯回現象。在風力機旋轉過程中，同一個攻角對應2個不同的阻力系數，其中，攻角變大過程中對應的阻力系數較大。對比上述2種情形可知：考慮動態失速影響所測得的翼型升力系數和阻力系數與靜態條件下風洞實驗結果有較大差異。所以，有必要對風輪在動態失速下的受力模型進行研究。

2 槳距角調節規律

H型垂直軸風力機屬于升力型垂直軸風力發電機，風作用在葉片上產生的切向力是風輪運轉的主要驅動力，它是葉片所受升力和阻力在切線方向上的合力。由翼型空氣動力學可知[11]，葉片的切向力隨攻角的變化而變化，在某一攻角處切向力會達到最大值。因此，計算最大切向力所對應的葉片攻角，進而通過這個攻角調節葉片槳距角使風輪獲得最大的風能利用率[12]。

2.1 葉片理論最佳攻角計算

本文采用的1 kW H型對稱翼垂直軸風輪模型如圖3所示，垂直軸風輪的相關參數如表1所示，計算時雷諾數仍選為=3.6×105。

對垂直軸風輪進行受力分解，得到作用在風輪上各力之間的關系如圖4所示。圖4中：為誘導速度和切向速度的合成風速；為風輪旋轉角速度；為葉片攻角，即合成風速方向與葉片弦線方向的夾角；為葉片槳距角，即切向速度方向與葉片弦線方向的夾角，可通過機構直接調節，此處=0°；為葉片方位角，當方位角位于0°~180°時，該區域稱為風輪的上風區，當位于180°~360°時，稱為風輪的下風區；L和D分別代表葉片運動時受到的升力和阻力，將L和D沿葉片運動的切向和法向正交分解，可得到葉片受到的切向力T和法向力N，其中切向力T是推動風輪運轉的主動力。以下討論當升力驅動風輪產生最大切向力T時葉片的攻角。

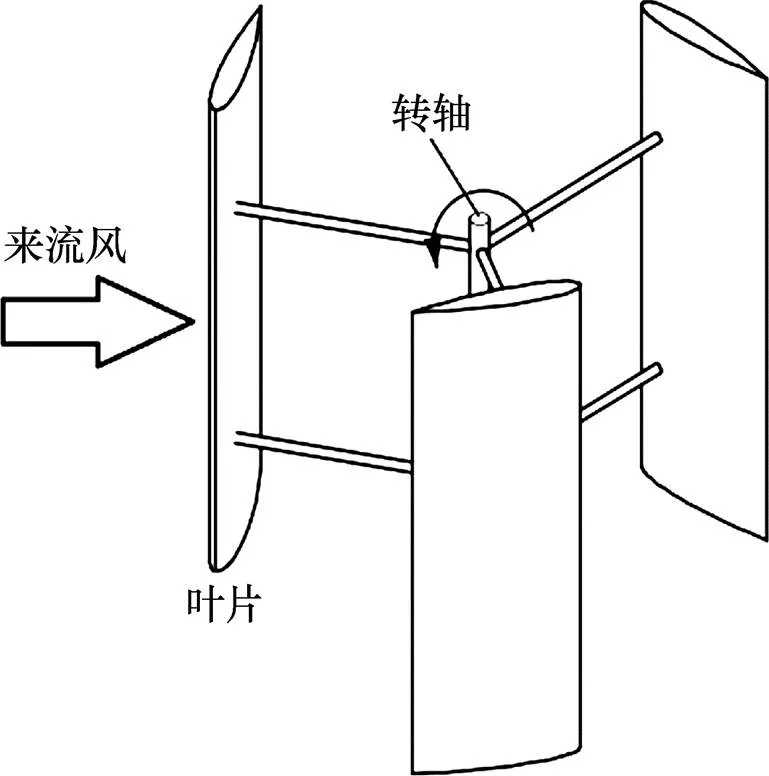
圖3 H型垂直軸風力機模型

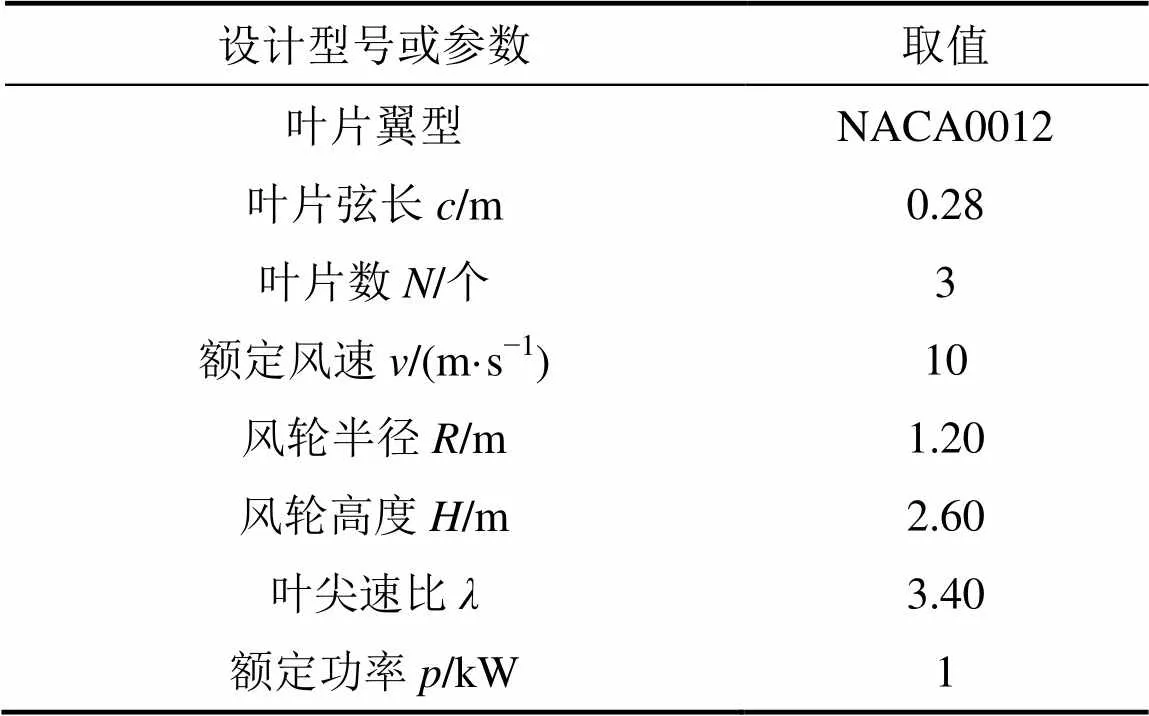
表1 垂直軸風力發電機的相關參數

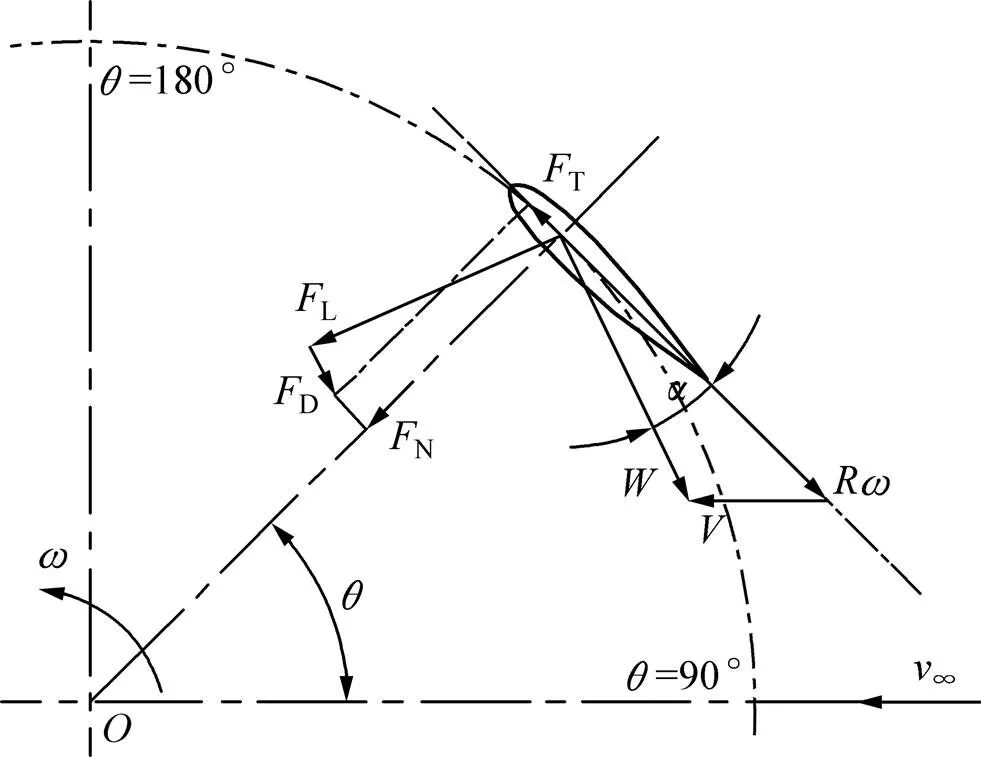
圖4 葉片受力分析圖

以葉片在風輪上風區為例，分析圖4中參數間的幾何關系，可以得出垂直軸風輪葉片攻角和合成風速間的表達式為

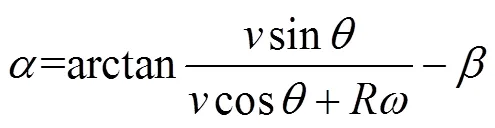
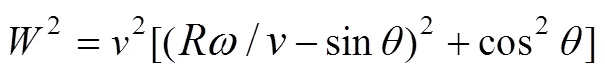
葉片所受的升力L和阻力D分別為[12]

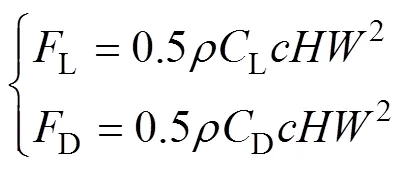
如圖4所示，L和D沿葉片切向運動的合力，即切向力T為

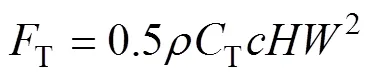
式中：為空氣密度，在標準大氣壓下取1.225 5 kg/m3；為葉片弦長；為翼型展向的長度；L和D分別為翼型的升力系數和阻力系數，其值可由NACA系列翼型空氣動力學特性數據庫查得；T為切向力系數，是L和D在弦長方向的合成值，它們之間的關系如圖5所示。

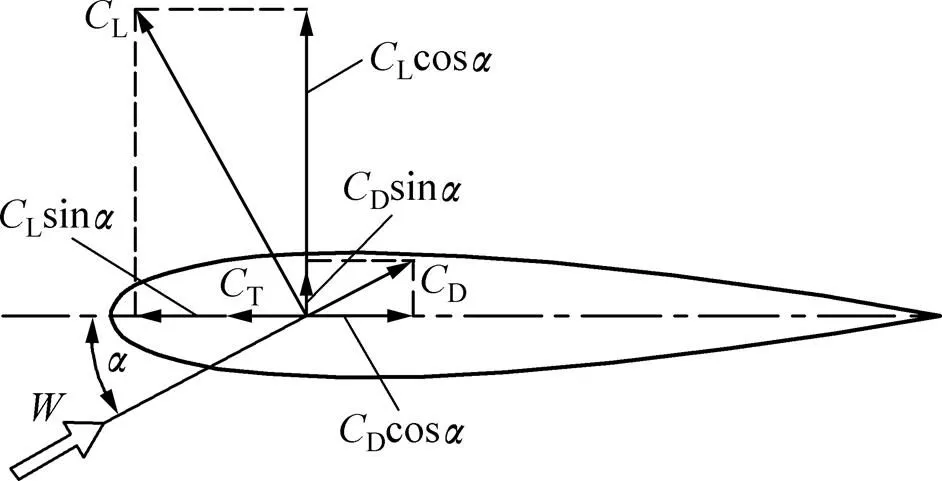
圖5 葉片翼型氣動力系數

由圖5中的幾何關系，得到T的計算式為

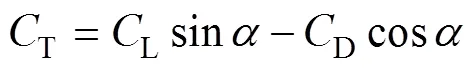
由式(4)和(5)可知：要求切向力FT，必須得到CL和CD。考慮到動態失速的影響，利用Sandia風力機的實驗結果，并結合式(5)得到升力系數CL、阻力系數CD和切向力系數CT隨攻角變化的圖形，如圖6所示。

由式(4)并結合圖6中的結果可計算出驅動風輪運轉的切向力T。風能利用率P為風輪的輸出功率與對應風輪的風功率max的比值，即

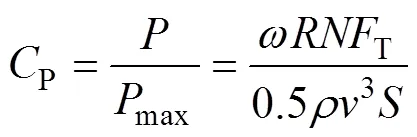
式中：為葉片數；為風輪的掃掠面積。由式(6)可知：在其他參數不變情況下，當葉片攻角的取值使切向力T達到最大時，風能利用率P也為最大值。由圖6可知：當攻角=14.8°時，切向力系數L達到最大值，即切向力T達到最大值，=14.8°就是考慮動態失速影響下葉片的最佳攻角。考慮到無論是上風區還是下風區，攻角都有逐漸變大的過程，所以，可以認為：在上風區，當攻角=14.8°時，切向力達到最大值；同理，在下風區，當攻角=?14.8°時，切向力達到最大值，對應的P也達到最大值，即風輪上風區和下風區的理論最佳攻角分別為14.8°和?14.8°。然而，目前的垂直軸風輪旋轉過程中葉片攻角隨方位角的變化呈類正弦規律[13]，不能始終保持在理論最佳攻角附近，故需要對槳距角進行調節，以此維持在最佳攻角處。為使計算結果更加精確，本文結合雙致動盤多流管理論對風輪槳距角的調節方法進行分析。

2.2 垂直軸風力機攻角及誘導速度計算

雙致動盤多流管模型是目前研究垂直軸風力機的主要分析模型[14]，經實驗驗證，該模型的計算精度較高。這里采用雙致動盤多流管理論計算垂直軸風輪各個方位誘導速度，從而得到葉片攻角的實際變化情況。雙致動盤多流管分析模型如圖7所示。

據圖7和雙致動盤多流管理論，無窮遠來流風∞流經垂直軸風輪時分為3個階段，分別為上風區誘導速度、轉軸處的均衡誘導速度e和下風區誘導速度′，其三者之間的關系為[11]

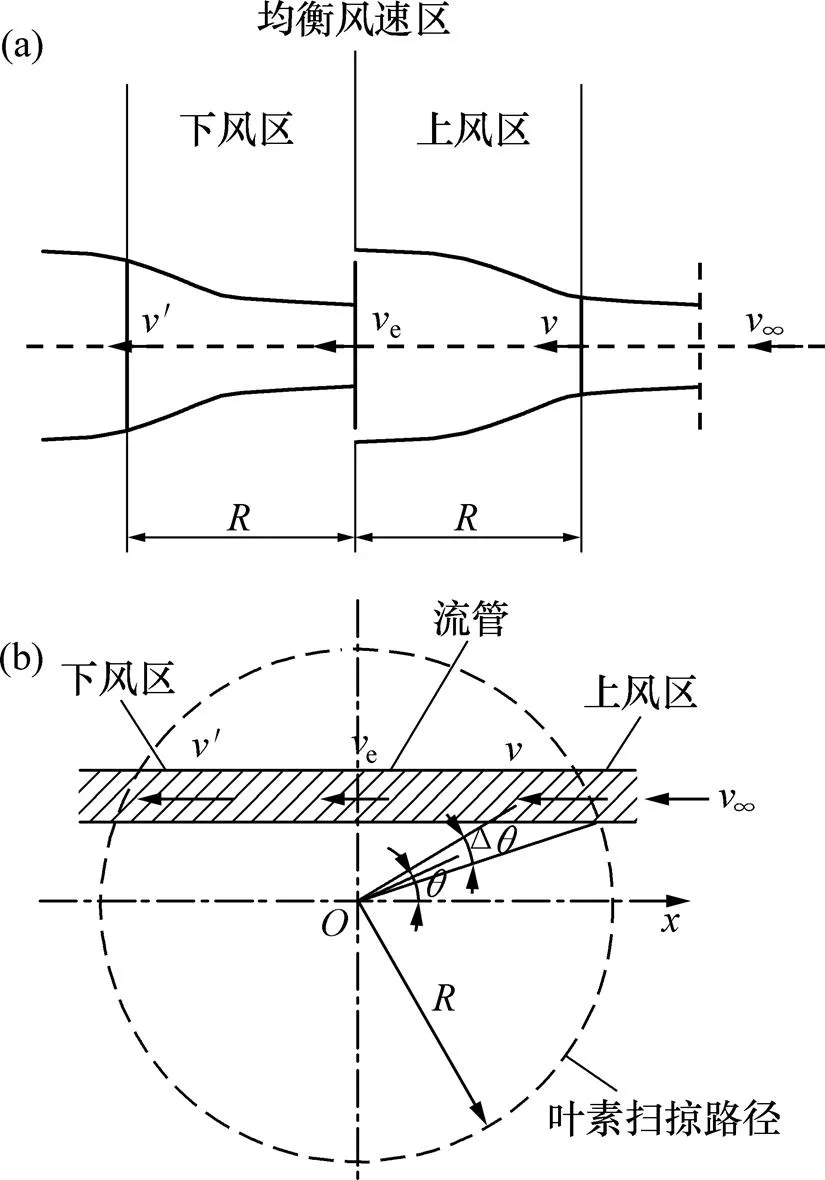
(a) 主視圖；(b) 俯視圖

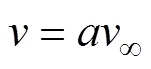
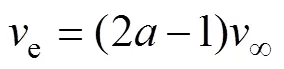
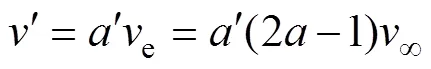
式中：和′分別為上風區誘導因子和下風區的誘導因子，且＜1，′＜1。

從方位角=0°開始記為第1個流管，假設模型共分為個流管，則第個流管的寬度為

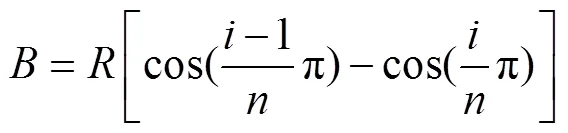
對每個流管進行受力分析，將流向力F分解為法向力N和切向力T，得到每個流管上的流向力為

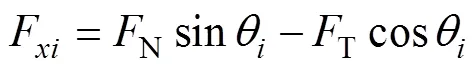
假設風輪葉片數為，流管總數為，則在風輪旋轉1周過程中，作用在個流管上的平均流向力為

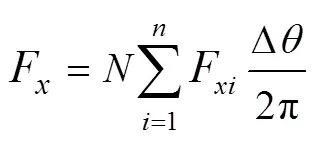
對每一個流管，建立連續方程、伯努利方程和動量方程，得到作用在流管上的平均流向力F為

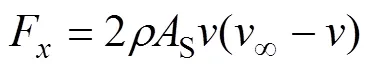
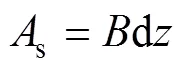
式中：為空氣密度(kg/m3)；s為流管面積；d為流管在豎直方向的高度。

由式(10)~(14)可得

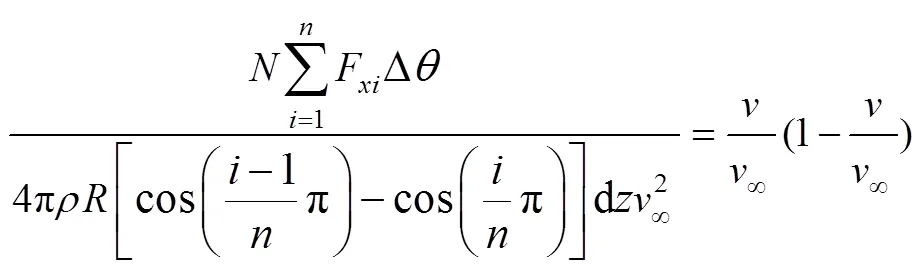
為了表達方便，將式(15)等號左邊部分記為*，結合式(10)，則*為

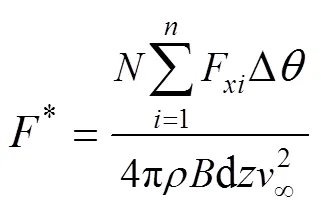
式(15)可以表示為

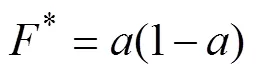
式(17)即為風輪上風區誘導因子的迭代公式。編制Matlab程序進行計算，令誘導因子a的迭代初值為1，殘差標準設置為10?4。當誘導因子迭代計算結果收斂后，分別用式(7)計算上風區各個方位的誘導速度，用式(2)計算合成風速W，結果如圖8所示。從圖8可以看出：合成風速隨方位角不斷變化，在方位角為180°時(如圖4所示)，由于切向速度的方向發生變化，合成風速的方向也發生了改變，但其大小未變。需要說明的是：上述H型垂直軸風力機的參數是在葉尖速比λ=3.40時得到的，在其他葉尖速比條件下，本文建立的雙致動盤多流管分析模型同樣適用。

2.3 槳距角調節方法

上述研究是在槳距角=0°時進行的。根據式(1)，葉片攻角隨方位角不斷變化，不能保證風輪在旋轉過程中保持理論最佳攻角。為提高風輪風能利用率，通過調節槳距角，達到間接改變攻角的目的。由式(1)可知葉片槳距角的表達式為

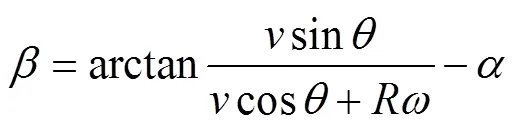
在上風區令葉片攻角等于14.8°，在下風區令葉片攻角等于?14.8°，據式(18)就能得到葉片槳距角的調節規律。由于此時調節槳距角后又會對上、下風區誘導速度的分布產生影響，故需重新利用雙致動盤多流管理論對調節槳距角后的模型進行迭代計算，求解新的攻角調節規律。重復此過程，直至得到的攻角與理論最佳攻角的殘差小于10?4為止，得出此時槳距角的調節規律如圖9所示。

按圖9所示的規律調節槳距角，得到變槳前后葉片攻角隨方位角的變化規律，如圖10所示。

從圖10可知：葉片槳距角調節前，攻角隨方位角呈類正弦規律變化，這與用矢量分析法所得的計算結果一致[15]；葉片變槳后，風輪上、下風區葉片攻角都能夠維持在最佳攻角處。

2.4 特殊方位角下槳距角調節規律修正

按此槳距角調節規律能夠很好地維持葉片攻角，但是由圖9可以看到，當方位角=0°和=180°時，由于風向突然改變，槳距角發生了跳變，而在實際調節過程中，這種跳變是很難實現的，因此，需要對上述槳距角調節規律進行修正。根據葉片氣動性能分析結果，在當前尖速比下，當方位角=0°和=180°，且葉片受到的升力沿風輪旋轉的徑向時，不能當作風輪旋轉推動力[16]。所以，在方位角為0°和180°時，將槳距角調節為0°，此時攻角為0°，葉片的阻力矩最小。圖11所示為修正后的葉片槳距角調節規律。

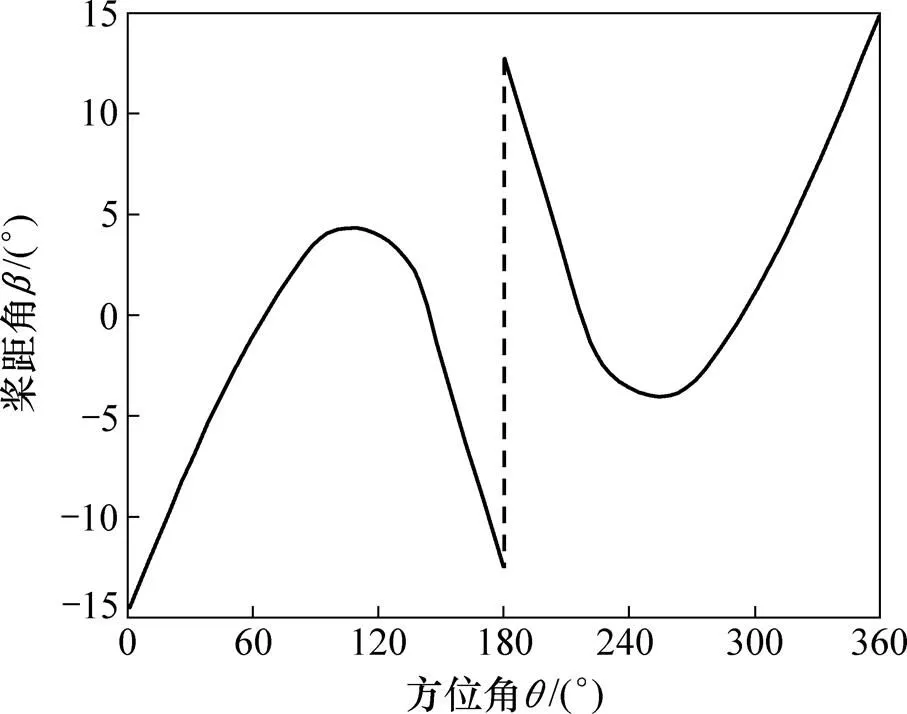
圖9 葉片槳距角調節規律

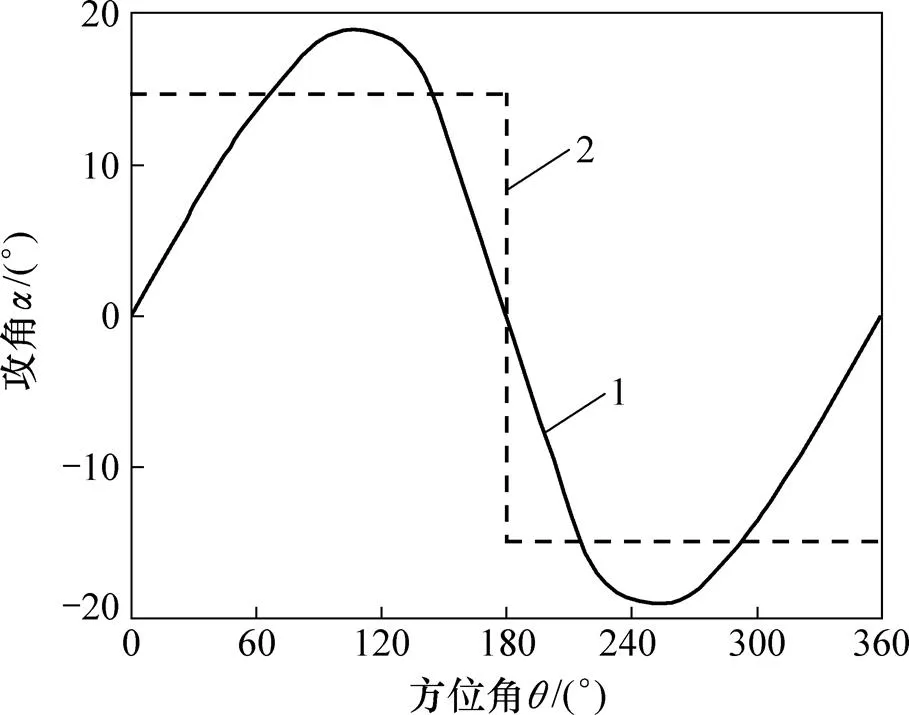
1—攻角調節前；2—攻角調節后。

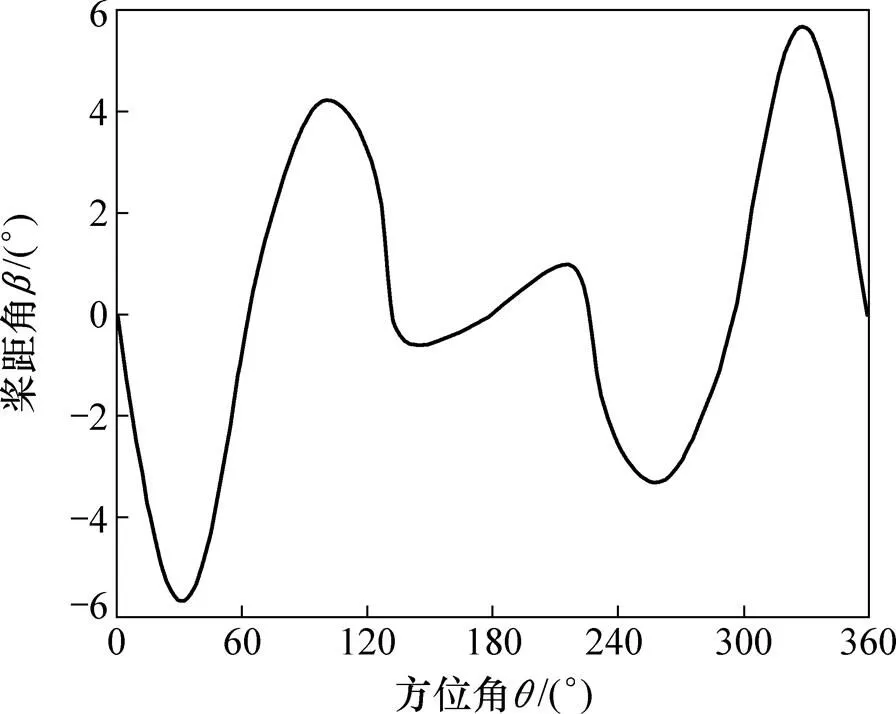
圖11 修正后的葉片槳距角調節規律

3 槳距角調節前后風力機性能對比

為了驗證本文提出的葉片槳距角調節規律的有效性，針對本文研究的H型垂直軸風輪模型，依據表1中風力機參數，利用雙致動盤多流管理論計算葉片槳距角調節前后風輪的切向力和風能利用率。

3.1 切向力對比

利用雙制動盤多流管理論計算上、下風區各流管的誘導速度，利用式(4)求得變槳距前后垂直軸風輪所受的切向力如圖12所示。從圖12可知：葉片槳距角調節后，當60°＜＜150°，225°＜＜290°時，切向力都較之前明顯增大，而在切向力小于變槳前的部分，2條曲線的差距不大。這說明這種變槳距規律能夠較好地提高垂直軸風力機的切向力，進而增大風輪的轉矩。

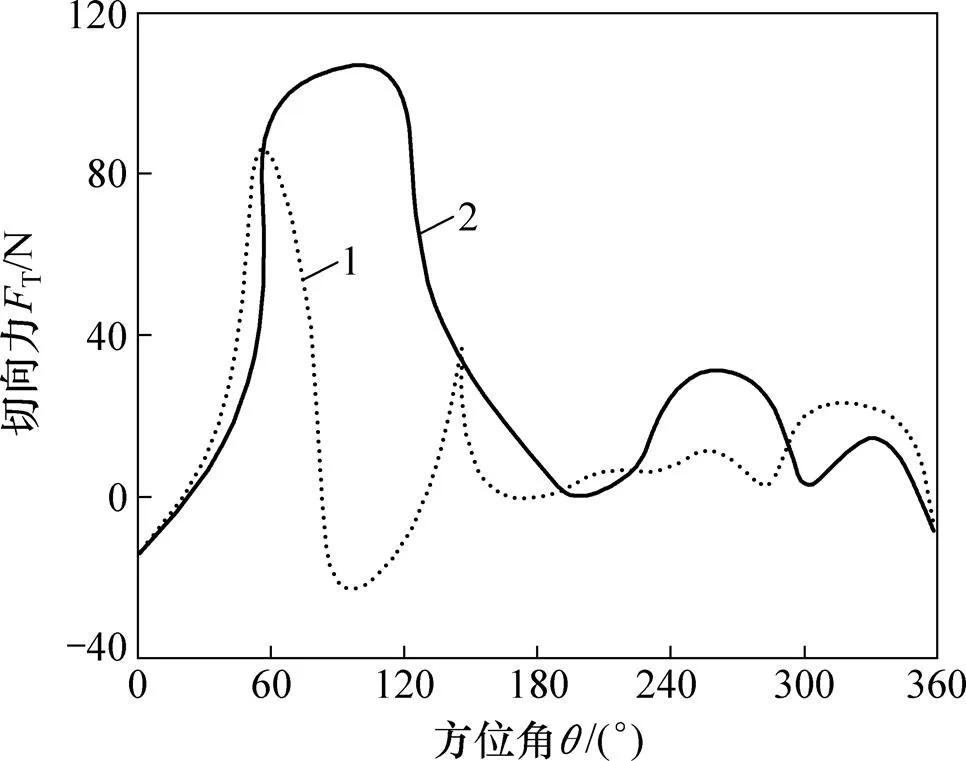
1—變槳距角前；2—變槳距角后。

3.2 風能利用率對比

為計算風輪的風能利用率，首先求解單個葉片對風輪主軸中心的轉矩為

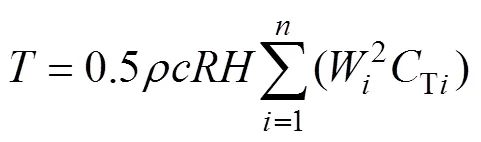
個葉片旋轉1周過程中產生的平均轉矩和平均輸出功率分別為

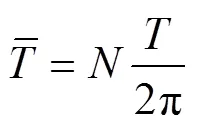
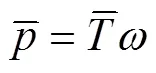
在此基礎上，風輪的風能利用率為

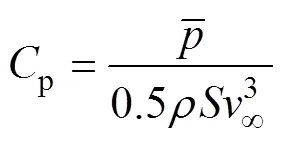
式中：為風輪掃風面積，對于垂直軸風力發電機，

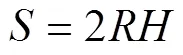
由式(19)~(23)，利用圖12中切向力并結合圖7中合成風速，即可計算出變槳前后垂直軸風力機的風能利用率。Matlab軟件編制的計算流程如圖13所示。計算結果顯示：由表1中的H型定槳距垂直軸風力機計算得到的風能利用率為34.6%；而采用本文提出的變槳距方案所得風能利用率為42.8%，可見變槳效果明顯。

4 結論

1) 以獲得最大切向力為目標，得到動態失速下本文研究的H型垂直軸風輪在上風區和下風區的理論最佳攻角分別為14.8°和?14.8°。

2) 利用雙致動盤多流管理論進行Matlab編程計算，得到風輪旋轉1周的變槳距規律。利用該變槳距規律，H型垂直軸風力機的風能利用率由變槳前的34.6%提高到42.8%，體現了該變槳距方法的有效性。

3) 考慮到特殊方位角下葉片升力沿風輪旋轉的徑向，為了減小阻力矩，規定0°和180°方位角的槳距角為0°，進一步明確了葉片變槳距變化規律。

[1] NOBUYUKI F, SATOSHI S. Observations of dynamic stall on Darrieus wind turbine blades[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(2): 201?204.

[2] 曹成帥, 趙允貴, 王太國. 一種新型獨立變槳控制器設計[J]. 電工電氣, 2016(12): 27?30. CAO Chengshuai, ZHAO Yungui, WANG Taiguo. Design of a new type of independent variable pitch controller[J]. Electrotechnics Electric, 2016(12): 27?30.

[3] 廉正光. 采用雙曲柄調距機構的垂直軸風力發電機機理研究與樣機設計[J]. 機械設計, 2016, 33(8): 100?104. LIAN Zhengguang. Principle research and prototype design of a vertical axis wind turbine with double crank adjustment mechanism[J]. Journal of Machine Design, 2016, 33(8): 100?104.

[4] 廉正光, 張宏偉, 李愷. 一種變槳距垂直軸風力發電機: 中國, 201410009955.3[P]. [2014?03?26]. LIAN Zhengguang, ZHANG Hongwei, LI Kai. A vertical axis wind turbine with variable pitch: China, 201410009955.3[P]. [2014?03?26].

[5] 趙振宙, 陳潘浩, 王同光, 等. 基于擾流技術的直葉片升力型垂直軸風輪的性能改善[J]. 機械工程學報, 2016, 52(22): 146?152. ZHAO Zhenzhou, CHEN Fanhao, WANG Tongguang, et al. Performance improvement of lift type wind turbine with straight blades based on interference airflow technology[J]. Journal of Mechanical Engineering, 2016, 52(22): 146?152.

[6] 梁云峰, 谷鳳民, 陳宇, 等. 變速恒頻風力發電機組液壓變槳距系統的設計與仿真[J]. 機床與液壓, 2017, 45(2): 63?68. LIANG Yunfeng, GU Fengmin, CHEN Yu, et al. Design and simulation for hydraulic variable pitch system of wind turbine with variable speed and constant frequency[J]. Machine Tool & Hydraulics, 2017, 45(2): 63?68.

[7] SHELDAHL R E. Aerodynamic characteristics of seven airfoil sections through 180 degrees angle of attack for use in aerodynamic analysis of vertical axis wind turbines[R]. Sandia: Sandia National Laboratories, 1981: 12?40.

[8] NOBUYUKI F, SATOSHI S. Observations of dynamic stall on Darrieus wind turbine blades[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(2): 201?214.

[9] 查顧兵. 風力機動態失速模型的研究及其在性能預測中的應用[D]. 上海: 上海交通大學機械與動力工程學院, 2009: 37?46. ZHA Gubing. Research and application of dynamical stall model in wind turbine[D]. Shanghai: Shanghai Jiaotong University. School of Mechanical Engineering, 2009: 37?46.

[10] ALLET A, PARASCHIVOIU I. Viscous flow and dynamic stall effects on vertical-axis wind turbines[J]. International Journal of Rotating Machinery, 1995, 2(1): 1?14.

[11] 伊恩·帕拉斯基沃尤. 垂直軸風力機原理與設計[M]. 李春, 葉舟, 高偉, 譯. 上海: 上海科學技術出版社, 2013: 62?86. PARASCHIVOIU I. Principle and design of vertical axis wind turbine[M]. LI Chun, YE Zhou, GAO Wei, trans. Shanghai: Shanghai Science and Technology Press, 2013: 62?86.

[12] CHOUGULE P, NIELSEN S. Overview and design of self-acting pitch control mechanism for vertical axis wind turbine using multi body simulation approach[C]//The Science of Making Torque from Wind. Lyngby, Denmark, 2014: 1?10.

[13] 張立軍, 劉華, 趙昕輝, 等. 垂直軸風力機非對稱翼型葉片變攻角方法[J]. 可再生能源, 2016, 34(2): 232?237. ZHANG Lijun, LIU Hua, ZHAO Xinhui, et al. The method for wind turbine to vary angle of attack of asymmetric airfoil blade[J]. Renewable Energy Resources, 2016, 34(2): 232?237.

[14] BLUSSEAU P, PATEL M H. Gyroscopic effects on a large vertical axis wind turbine mounted on a floating structure[J]. Renewable Energy, 2012, 46(5): 31?42.

[15] 張立軍, 劉華, 趙昕輝, 等. 垂直軸風力機非對稱翼型葉片變攻角方法[J]. 可再生能源, 2016, 34(2): 232?237. ZHANG Lijun, LIU Hua, ZHAO Xinhui, et al. The method for wind turbine to vary angle of attack of asymmetric airfoil blade[J]. Renewable Energy Resources, 2016, 34(2): 232?237.

[16] KIRKE B K, LAZAUSKAS L. Limitations of fixed pitch Darrieus hydrokinetic turbines and the challenge of variable pitch[J]. Renewable Energy, 2011, 36(3): 893?897.

(編輯 陳燦華)

Real-time variable-pitch control laws of H-type vertical axis wind turbine under dynamic stall

ZHANG Lijun1, MA Dongchen1, ZHAO Xinhui1, MI Yuxia1, ZHANG Song2, WANG Hanxiang1, JIANG Hao1

(1. College of Electromechanical Engineering, China University of Petroleum, Qingdao 266580, China; 2. College of Chemical Engineering, China University of Petroleum, Qingdao 266580, China)

Aiming at the disadvantages of low efficiency and poor self-starting ability of vertical axis wind turbine, the study takes 1 kW H-type vertical axis wind turbine as the research object, the influence of dynamic stall on pitch angle adjustment was analyzed by contrasting the experimental results of wind turbine measured by dynamic stall at Sandia National Laboratory. The maximum tangential force of the wind wheel was regarded as the target, and the theoretical optimum angles of attack 14.8° and ?14.8° at upwind area and downwind areas of wind turbine were obtained, respectively. In order to keep the wind wheel near the optimum angle of attack, the programming calculation in Matlab software based on double-multiple streamtubes theory was carried out, and the force model of the wind turbine was established and the pitch angle of the vertical axis wind turbine in each direction was obtained. By adjusting the pitch angle of 0° and 180° azimuth angle, the rule of the variable pitch of a vertical axis wind turbine was given. Finally, the proposed real-time variable-pitch control laws were verified based on the multi flow management theory of double actuated disk. The results show that the wind energy utilization rate can be increased from 34.6% to 42.8% by using the variable pitch.

vertical axis wind turbine; dynamic stall; pitch angle; optimum angle of attack; double-multiple stream tubes

10.11817/j.issn.1672?7207.2018.10.030

KT83

A

1672?7207(2018)10?2610?08

2017?11?18；

2018?01?12

山東省自然科學基金資助項目(ZR2014EEP022)；中央高校基本科研業務專項資金資助項目(17CX05021)(Project (ZR2014EEP022) supported by Natural Science Foundation of Shandong Province; Project(17CX05021) supported by the Fundamental Research Funds for the Central Universities)

張立軍，博士，教授，碩士生導師，從事可再生能源技術和綠色裝備制造研究；E-mail：zhanglijun@upc.edu.cn