材料應變率效應對2類吸能結構碰撞性能的影響

馮悅，肖守訥，朱濤，楊冰，楊皓杰

?

材料應變率效應對2類吸能結構碰撞性能的影響

馮悅，肖守訥，朱濤，楊冰，楊皓杰

(西南交通大學 牽引動力國家重點實驗室，四川 成都，610031)

軌道車輛吸能結構變形時伴隨著明顯的應變率效應，為了研究材料應變率效應對碰撞仿真結果的影響，以應變率敏感材料Q235為研究對象，首先，通過實驗數據對比和理論解對比2種方法，證明考慮應變率效應的Q235材料模型的可靠性；然后，研究材料應變率效應對擠壓式和壓潰式圓錐管吸能結構碰撞載荷與吸能、變形模式等耐撞性能的影響；在此基礎上，提出2種受材料應變率效應的影響不明顯、變形有序可控的誘導式吸能結構。研究結果表明：對于不同結構，材料應變率效應影響因子不同，考慮材料應變率強化效應的擠壓式吸能結構碰撞力放大因子比壓潰式圓錐管結構的大；對于不同結構，材料應變率效應影響因子隨速度變化的幅度不同，擠壓式吸能結構的應變率效應放大因子隨速度變化幅度比壓潰式的小；材料應變率效應對第二類吸能結構的變形模式影響顯著，應變率強化效應減少了應變率較大的變形，增加或促進了應變率較小的變形；誘導式吸能結構的變形模式受材料應變率效應的影響不明顯，變形有序可控，在工程設計中可考慮采用誘導結構，以減少材料應變率效應對結構變形模式的影響。

軌道車輛；碰撞性能；吸能結構；應變率效應

吸能結構在軌道車輛碰撞過程中主要通過塑性變形吸收能量，其吸能性能與軌道車輛碰撞響應關系密切，是軌道車輛被動安全中非常重要的部分[1?7]。由于碰撞過程中沖擊速度較大，在塑性變形過程中伴隨著明顯的應變率效應。然而，目前進行軌道車輛碰撞仿真時一般未考慮材料的應變率效應，已有研究表明材料的應變率效應會對結構碰撞性能產生明顯的影響。廖其紅等[8]針對閉口帽型薄壁梁在軸向碰撞載荷下的壓潰折曲過程進行了研究，對比有限元計算結果與實驗結果發現考慮材料應變率效應會使結構吸能特性與實驗結果更接近，應變率是造成碰撞實驗和準靜態壓縮實驗結果差異的最主要原因。孟廣成等[9]在對護欄的碰撞仿真研究中發現考慮應變率影響比不考慮應變率影響的仿真結果與實驗結果更加接近。王自力 等[10?13]研究了材料應變率效應對汽車和船舶碰撞中簡單結構和復雜結構的碰撞影響，結果表明材料的應變率效應對簡單結構的影響比較明顯，會改變結構變形模式、失效模式等，但對復雜結構的影響不明顯，同時，材料的應變率強化效應會增大結構的壓潰力，提高結構的承載能力和吸能結構的吸能能力。而楊超等[14]在對軌道車輛吸能結構應變率效應影響的研究中得出5083H111鋁合金的負應變率敏感性會減少結構的吸能量。目前關于材料應變率效應影響的研究多集中于壓潰式結構，而且大多未對其影響進行深入分析，而軌道車輛吸能結構種類繁多，變形模式多樣，僅研究壓潰式結構受材料應變率效應的影響是不夠的。根據CALLADINE等[15]的研究指出，吸能結構可以根據碰撞力位移曲線的特征分為2類：第一類吸能結構的碰撞力位移曲線在沖擊發生開始階段迅速增加，隨著沖擊進行，碰撞力波動很小，基本保持平穩；第二類吸能結構的碰撞力迅速增加之后有1個明顯峰值，下降后隨著沖擊進行明顯波動。這2類吸能結構的變形模式具有不同的碰撞速度敏感性[16]。軌道車輛中常用的第一類吸能結構主要有擠壓式、膨脹式、翻卷式等，第二類吸能結構主要為壓潰式[17?19]。對于第一類吸能結構，翻卷式吸能結構的翻卷變形對材料、結構要求嚴格，變形模式不易發生；膨脹式吸能結構軸向占用空間大；擠壓式吸能結構的變形穩定、有序，是理想的吸能結構。第二類吸能結構主要是各種截面的壓潰結構，不同截面壓潰式吸能結構中圓錐管的壓潰可控性更強，綜合耐撞性能更優。本文作者主要研究對比材料的應變率強化效應對擠壓式吸能結構和壓潰式圓錐管吸能結構軸向碰撞性能的影響，并分析產生差異的原因，進而指導工程中吸能結構設計。

1 材料模型

為了更清晰地表現材料應變率效應對結構碰撞性能的影響，使用典型的應變率敏感材料Q235。材料模型為彈塑性本構模型，通過廣義Cowper?Symonds模型考慮應變率效應，公式為

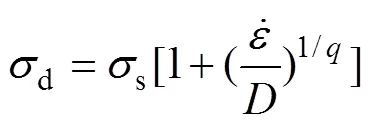
式中：d和s分別為高應變率下的動態流動應力和準靜態流動應力；和為應變率相關的材料參數。對于Q235低碳鋼，屈服極限為235 MPa，切線模量設為2 GPa。在考慮應變率強化效應時，=6 844 s?1，=3.91[13]；未考慮應變率強化效應時，=0 s?1，=0。

2 模型驗證

利用顯式動力學軟件LS-DYNA進行有限元仿真計算。為保證計算結果的可靠性，首先從2個方面驗證本文有限元仿真計算方法的可靠性。

2.1 與實驗結果比較

采用上述材料模型，將同等條件下是否考慮該材料應變率效應的仿真結果與實驗結果進行對比。有限元仿真計算結構與文獻[13]中沖擊實驗結構一致，均是長度為500 mm、外徑為250 mm、壁厚為6 mm的圓筒，且在距底板30 mm處設置寬為10 mm、深為 3 mm的初始缺陷，沖擊質量為1 030 kg，初始速度為17.8 m/s。有限元仿真計算模型如圖1所示，壓潰載荷計算結果對比如圖2所示。

由圖2可知：在考慮Q235材料的應變率強化效應時，仿真結果與實驗結果的峰值壓潰載荷基本吻合，仿真結果的平均壓潰載荷大于實驗值，相對誤差為6.8%；而未考慮材料的應變率強化效應時，初始峰值載荷明顯小于實驗值，平均壓潰載荷偏小，壓潰位移偏大。經對比發現：在考慮材料的應變率強化效應后，仿真計算得到的峰值載荷以及載荷?位移曲線的變化趨勢與實驗結果更接近。由于有限元仿真計算中使用的材料本構模型通過實驗結果擬合得到，與實際實驗中材料本身力學性能存在微小差異，故結構變形與實際變形不完全相符。但由于相對誤差較小，本文使用的材料模型、有限元模型及計算方法均可以用于工程仿真研究。

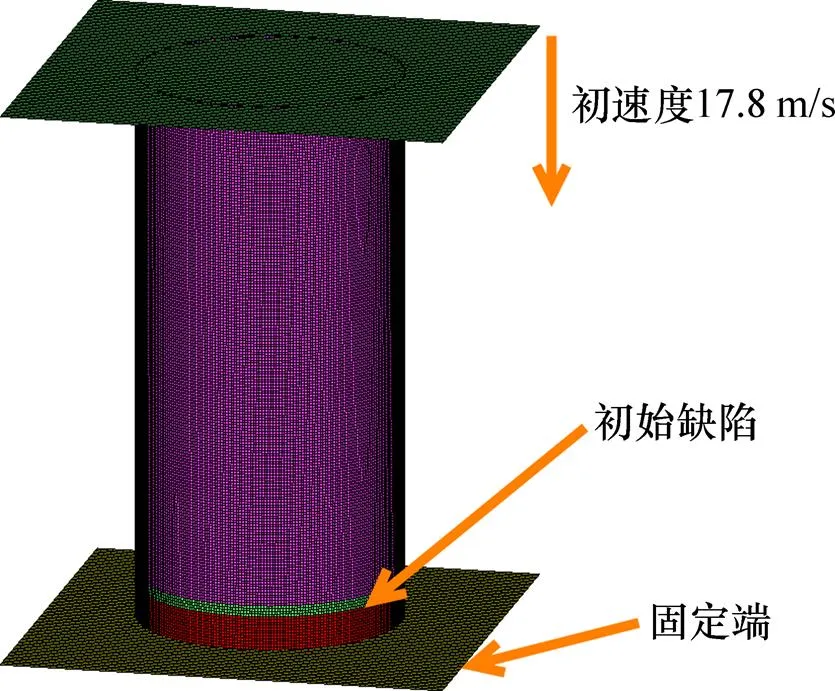
圖1 與實驗對比的有限元模型

2.2 與理論解比較

薄壁圓管軸向壓潰的塑性破損模式主要包括3種：圓環模式、鉆石模式和混合模式。國外對圓管壓潰變形的理論研究較多，故本文先以圓管壓潰結構為研究對象，通過有限元仿真計算研究圓管壓潰結構受材料應變率強化效應的影響，并與理論解進行比對。

圓管外徑為150 mm，壁厚為3 mm，軸向長度為200 mm。使用的單元為Belytschko-Tsay薄殼單元，沿厚度方向取4個積分點，單元基本尺寸為2 mm，沖擊速度設定為恒速，依次為3，6，9，12和15 m/s。

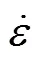
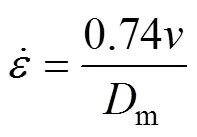
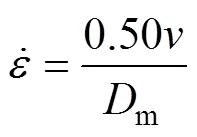
式中：為沖擊速度；m為圓管直徑。由此可以計算出在某一沖擊速度下的理論平均應變率，并根據式(4)和仿真計算的未考慮材料應變率效應時的平均壓潰載荷計算考慮后結構的理論動態平均壓潰載荷[20]。

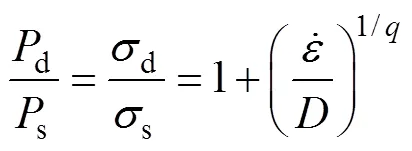
式中：d為動態平均壓潰載荷，即考慮了材料應變率強化效應后的平均壓潰載荷；s為靜態平均壓潰載荷，即不考慮材料應變率效應時的平均壓潰載荷。

在計算平均壓潰載荷時，有效壓潰行程為吸能效率最大值所對應的壓縮行程[21]。

將動態平均壓潰載荷的理論計算值與仿真計算值進行對比，見表1。從表1可見：動態平均壓潰載荷理論計算結果與考慮材料應變率效應的仿真計算結果的最大相對誤差在10%以內，對工程研究來說精度 足夠。

綜上可知：本文采用的材料模型、有限元模型及計算方法是可靠的，可以用于研究材料應變率效應對其他吸能結構碰撞性能的影響。

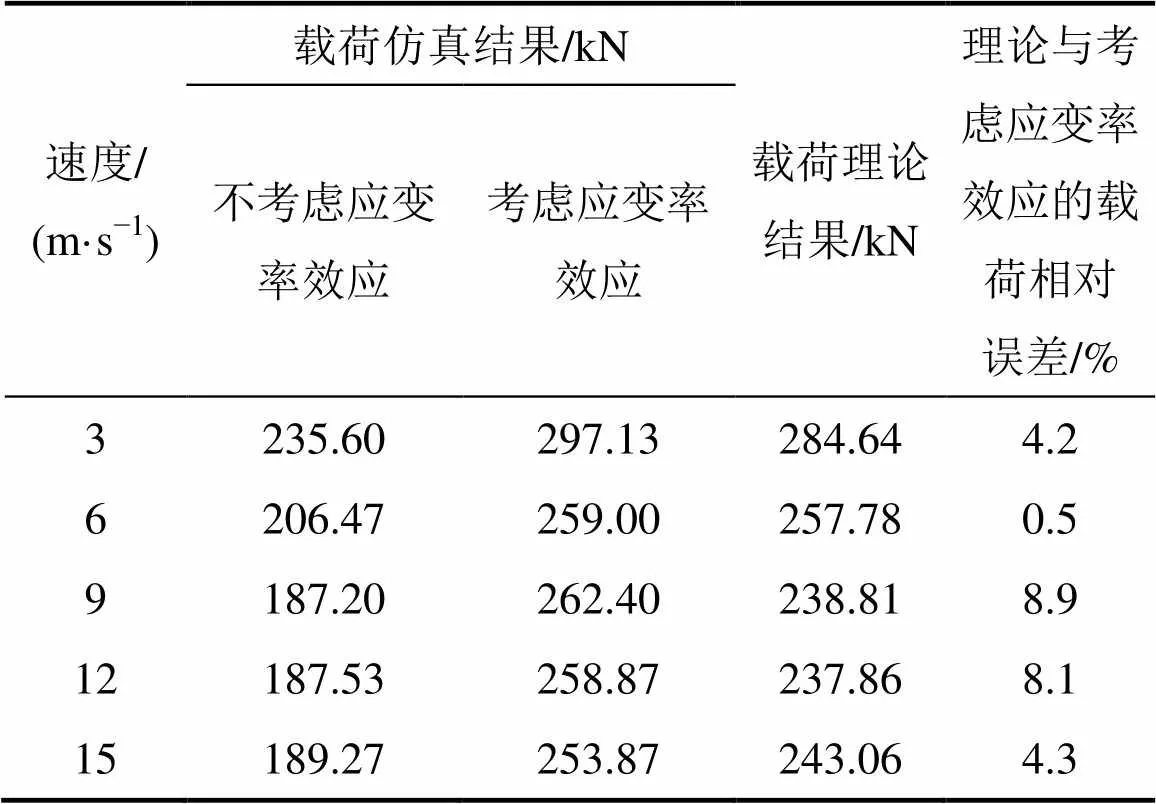
表1 平均壓潰載荷對比

3 計算模型與邊界條件

對于2種吸能結構，參照軌道車輛吸能結構常用軸向長度，設計軸向長度為470 mm，發生塑性變形的薄壁厚度為3 mm，單元相關設置與模型驗證時保持一致。

對于擠壓式吸能結構，小端外徑為135 mm，大端外徑為145 mm，通過圓弧光滑過渡；對于壓潰式圓錐管：小端外徑為105 mm，大端外徑為145 mm。2類吸能結構模型如圖3所示。

圖3 2類吸能結構模型

本文主要研究2類吸能結構在軸向正面碰撞下的吸能特性。具體邊界條件設置為：法蘭座和安裝座固定不動，防爬齒部分以恒速沖擊擠壓管和壓潰管，沖擊速度分別取5，10和15 m/s，并且在每個模型中沿母線標記距離防爬齒板分別為75，250和370 mm的前、中、后部3個不同位置的單元用于碰撞性能分析。

4 計算結果及分析

4.1 碰撞載荷與吸能

4.1.1 計算結果

2種不同吸能結構的碰撞力?位移曲線見圖4，其中擠壓式吸能結構有效擠壓行程均按384 mm(防爬齒板接觸法蘭座)計算，壓潰式吸能結構的有效壓潰行程取值方法與模型驗證時一致。

從圖4可見：擠壓式吸能結構的擠壓力?位移曲線比較平穩，僅存在微小波動；在材料應變率強化效應影響下，瞬時擠壓力與平均擠壓力整體提升，但碰撞載荷歷程未發生明顯改變。

壓潰式圓錐管吸能結構的壓潰力?位移曲線受材料應變率強化效應的影響比較顯著，在考慮材料應變率強化效應之后，結構峰值壓潰力和平均壓潰力明顯增大，壓潰力歷程出現明顯差異，峰值和谷值的數量和位置發生改變，褶皺形成的時間和數量發生改變。

(a) 擠壓式；(b) 壓潰式

2種不同結構在有效吸能過程中的總吸能見圖5。從圖5可知：在考慮材料的應變率強化效應后，擠壓式吸能結構和壓潰式圓錐管結構的總吸能均比未考慮時的大。

將2種不同結構在有效吸能過程中的平均碰撞力進行對比，發現在考慮材料的應變率強化效應之后，擠壓式吸能結構的平均擠壓力和壓潰式圓錐管結構的平均壓潰力也均比未考慮時的大。

對于擠壓式吸能結構，不同沖擊速度下有效擠壓行程保持不變，而擠壓總吸能可表示為有效擠壓行程與平均擠壓力的乘積，故平均擠壓力與總吸能的放大因子相同。

對于壓潰式圓錐管結構，有效壓潰行程因考慮材料應變率強化效應而增加，故總吸能的放大因子略大于平均壓潰力放大因子，壓潰式圓錐管結構的平均壓潰力如表2所示。

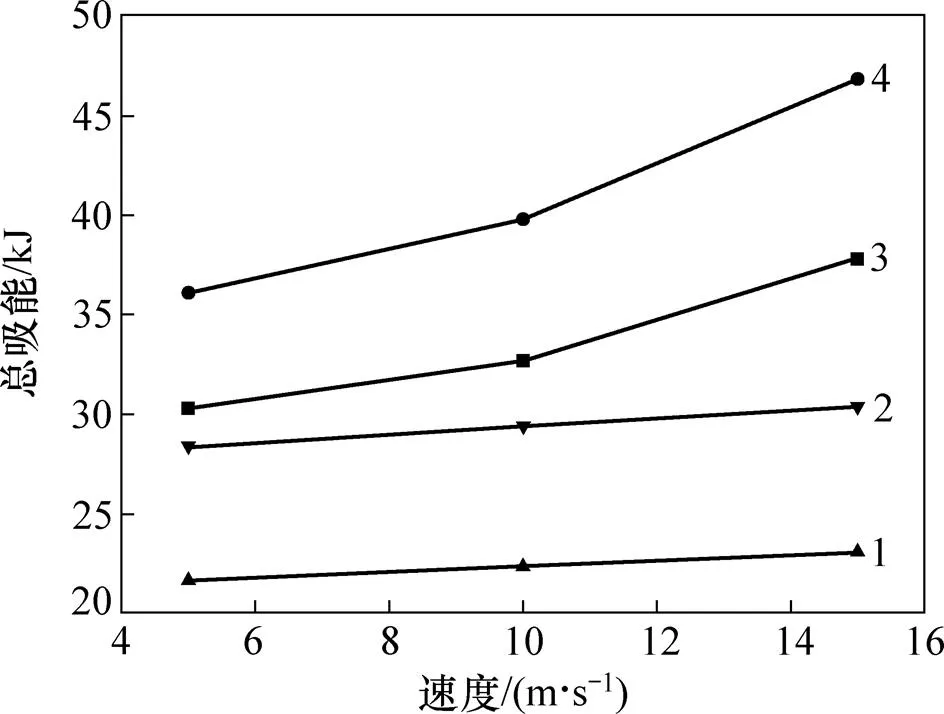
1—未考慮應變率，擠壓式；2—考慮應變率，擠壓式； 3—未考慮應變率，壓潰式；4—考慮應變率，壓潰式。

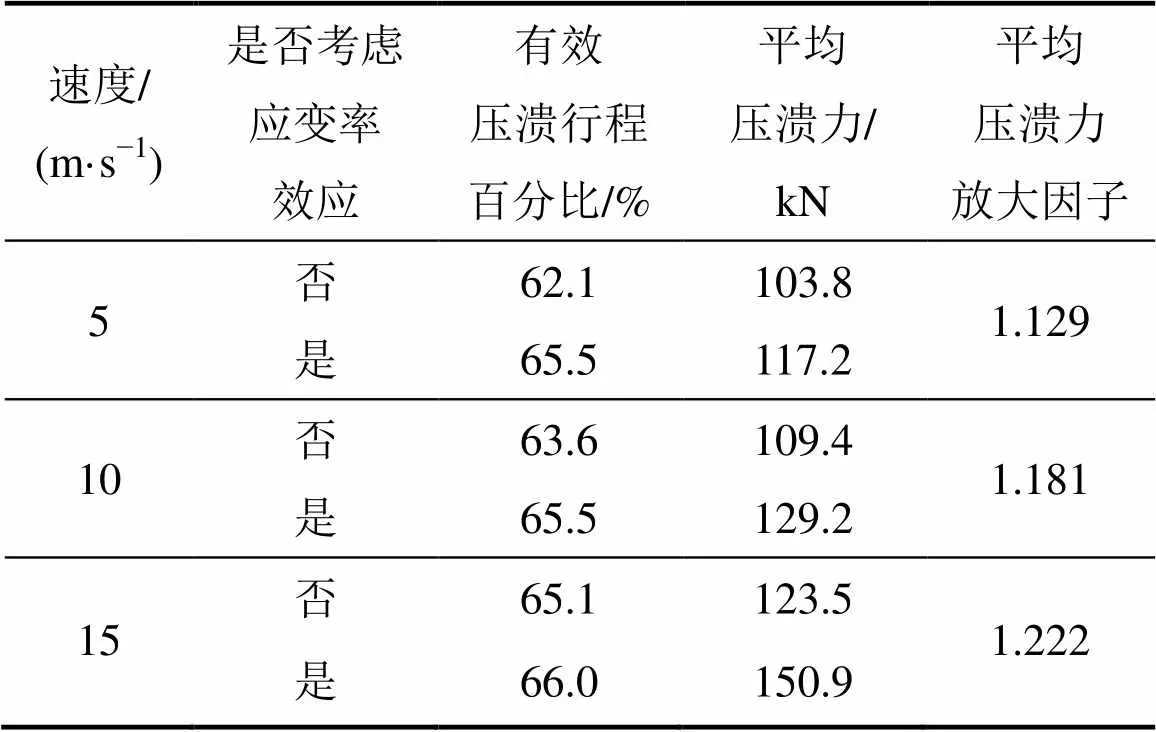
表2 壓潰式圓錐管吸能結構平均壓潰力統計

4.1.2 討論與分析

對不同速度下的總吸能放大因子和平均應變率進行比較，其中平均應變率取值為有效吸能過程中結構母線上典型位置處單元應變率的統計平均值，如圖6所示。從圖6可見：擠壓式吸能結構的總吸能放大因子和平均應變率隨沖擊速度的增加變化幅度很小，壓潰式吸能結構比前者變化幅度更大；在速度以5 m/s的間隔變化時，壓潰式吸能結構的應變率以6 s?1的速度增加，擠壓式吸能結構的增加速度只有1 s?1。為進一步確認擠壓式吸能結構沖擊速度與總吸能放大因子的關系，對該結構進行速度為30 m/s的碰撞仿真，此時，平均應變率為6.65 s?1，放大因子為1.336，與其他速度相比明顯提高。仿真結果表明：隨速度同等增大，壓潰式圓錐管結構比擠壓式結構的平均應變率和總吸能放大因子變化更明顯。

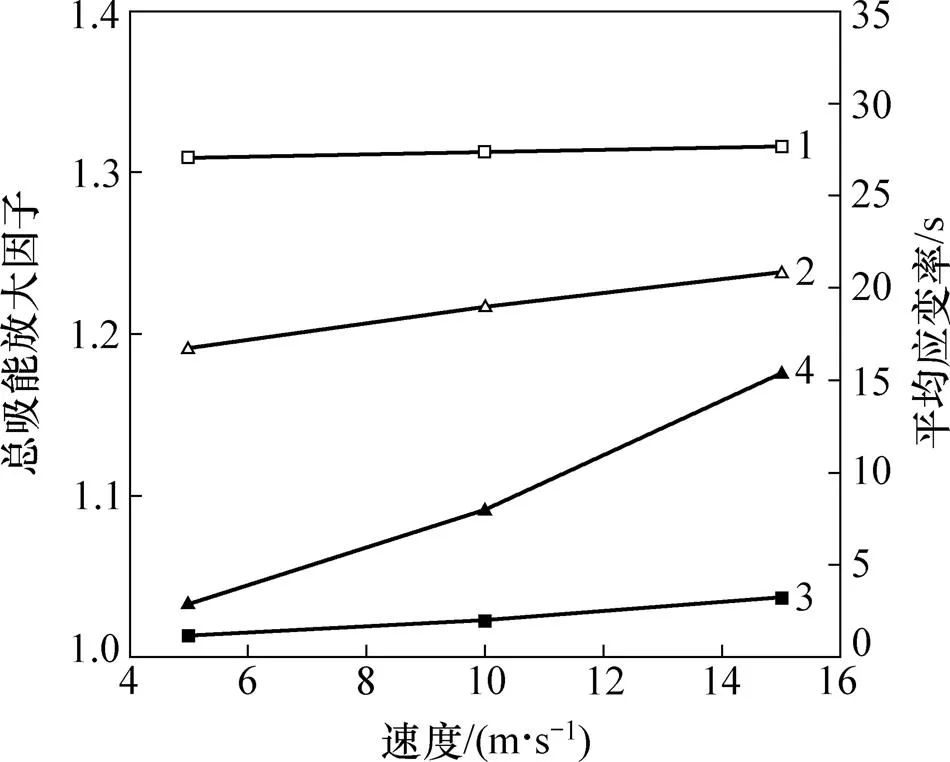
1—放大因子，擠壓式；2—放大因子，壓潰式； 3—平均應變率，擠壓式；4—平均應變率，壓潰式。

雖然擠壓式吸能結構平均應變率及其總吸能放大因子對速度變化不敏感，擠壓力歷程受材料應變率強化效應的影響也不明顯，但擠壓式吸能結構因材料應變率強化效應帶來的平均擠壓力放大因子比壓潰式吸能結構壓潰力放大因子更大。下面對2種結構分別從碰撞力理論計算角度進行分析。

對于壓潰式圓錐管結構，其在圓環變形、鉆石變形或者混合變形模式下，假設材料為理想剛塑性，平均壓潰力均可以表示成如下形式[22?23]：

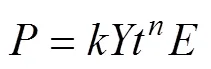
式中：為結構平均壓潰力；為材料的靜態屈服應力；為壁厚；和為與應力無關，與直徑、厚度和錐角相關的系數，對于不同變形模式，該系數不同；為與結構相關的相應實數。式(5)與圓管壓潰平均壓潰力的表達形式一致，故在結構有效壓潰行程不變情況下，結構的平均壓潰力或總吸能的放大因子與材料流動應力放大因子一致，動、靜態平均壓潰載荷之間均可通過式(4)計算平均壓潰力理論放大 因子。

圓錐管的平均應變率沒有理論計算公式，故取仿真結果的平均值，同時利用式(4)計算平均壓潰力放大因子并與仿真結果進行對比，見表3。從表3可見：圓錐管的平均壓潰力放大因子的理論計算結果與仿真計算結果基本吻合，最大相對誤差為1.0%，說明有限元仿真能準確地表征薄壁圓錐管在動態軸向壓縮時的碰撞性能。

但對于擠壓式吸能結構，材料應變率效應使結構平均擠壓力放大因子比材料自身流動應力放大因子大得多，見表4。

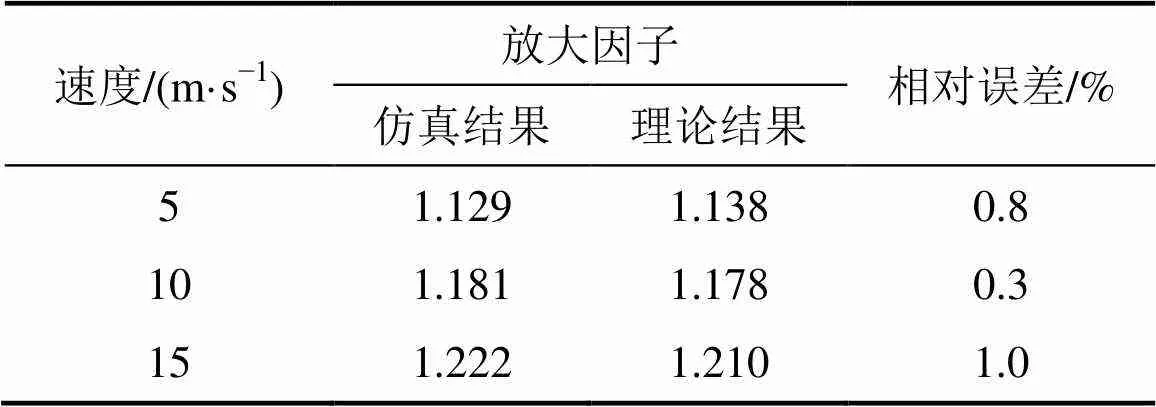
表3 壓潰式圓錐管理論與仿真平均壓潰力放大因子對比

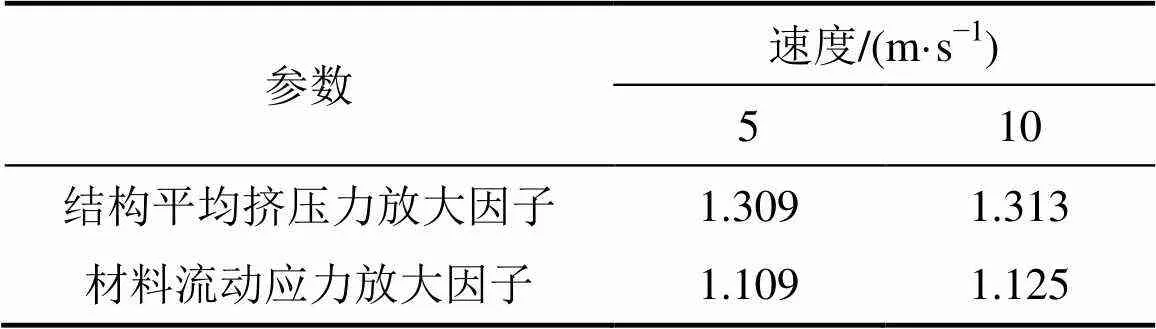
表4 結構平均擠壓力與材料流動應力放大因子對比

擠壓式吸能結構可視為向內膨脹式吸能結構[24]，擠壓式和膨脹式吸能結構的變形過程均包括彎曲、縮徑(擴徑)、摩擦3部分。緩沖力模型不能用類似于式(5)的形式表達[25]，與壓潰式結構由材料應變率效應引起的碰撞力放大因子存在差異。

與壓潰式吸能結構僅依靠塑性變形吸能不同，擠壓式吸能結構能量吸收由塑性變形吸能與摩擦耗能2部分組成。不同吸能的放大因子對比見圖7。從圖7可見：考慮了材料的應變率強化效應時，摩擦耗能的放大因子大于塑性變形吸能的放大因子，總吸能放大因子提高。

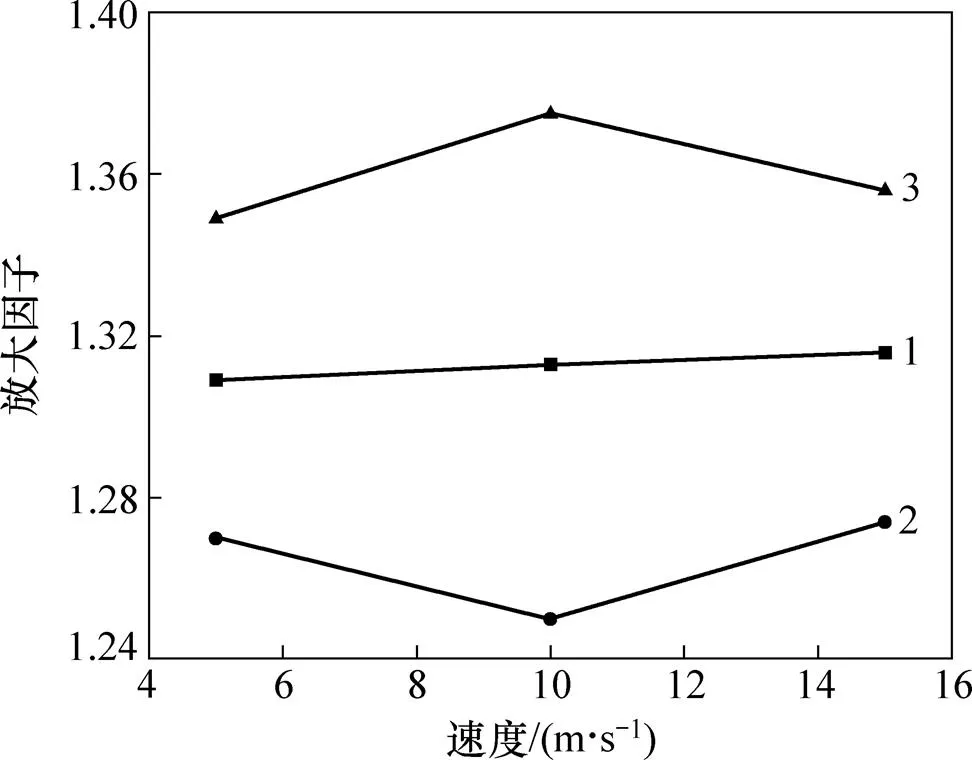
1—總吸能；2—塑性變形吸能；3—摩擦耗能。

綜上所述，由于存在擠壓式吸能結構特殊的變形模式，同時考慮擠壓管與法蘭座之間的摩擦耗能，故在考慮材料應變率強化效應后結構的平均擠壓力放大因子大于材料流動應力放大因子。但以上僅為定性分析結果，針對擠壓式吸能結構平均擠壓力受材料應變率強化效應的影響有待深入研究。

以上對比結果表明考慮材料應變率強化效應后結構的平均壓潰力或擠壓力放大因子與結構的變形模式密切相關。在變形過程中，應變較大的結構通常伴隨著較高的應變率，如壓潰式結構等第二類吸能結構對速度的敏感性較強，變形應變率及壓潰力或總吸能放大因子隨速度改變發生明顯變化；而對于應變較小、變形穩定的擠壓式等第一類吸能結構，應變率通常較小，應變率及相應的放大因子對速度變化不敏感。但考慮材料應變率強化效應引起的結構吸能或平均碰撞力的放大因子與結構速度敏感性不成正相關，而是取決于結構變形機理及吸能方式。

4.2 初期變形模式

4.2.1 計算結果

考慮材料的應變率強化效應會對結構的初始變形產生影響。無論是擠壓式吸能結構還是壓潰式圓錐管吸能結構，在考慮材料應變率強化效應之后，變形初期產生塑性應變的單元數目均會增多，如圖8和圖9所示。

4.2.2 討論與分析

對于擠壓式吸能結構，在考慮材料的應變率強化效應時，擠壓后端壓潰鼓脹產生的塑性應變比不考慮時的小，但產生塑性應變的單元數目增多，見圖8所示的擠壓后端應變云圖。由于壓潰鼓脹變形應變率較大，材料的流動應力增加明顯，增強了端部的抵抗能力，使壓潰鼓脹變形減小，軸向壓縮變形增加。同理，前端擠壓變形包括彎曲、軸向壓縮以及徑向收縮，彎曲變形應變率最大，故與擠壓后端一致，彎曲變形減小，徑向收縮變形與軸向壓縮變形增大，總體表現為單元塑性應變減小但產生塑性應變的單元數目 增多。

對于壓潰式圓錐管結構，在3種速度下，未考慮材料應變率強化效應時，初始時刻均已形成塑性鉸，如圖9所示。該部分應變和應變率較大，在考慮材料應變率強化效應后繞塑性鉸轉動變形所需要的力明顯增大，所以，在同樣的軸向力作用下，繞塑性鉸的轉動變形一部分轉變為應力增加較小的軸向壓縮變形，表現為未形成初始塑性鉸或形成滯后，應變向后傳遞，在應變云圖上表現為產生初始塑性應變的單元數目增多。

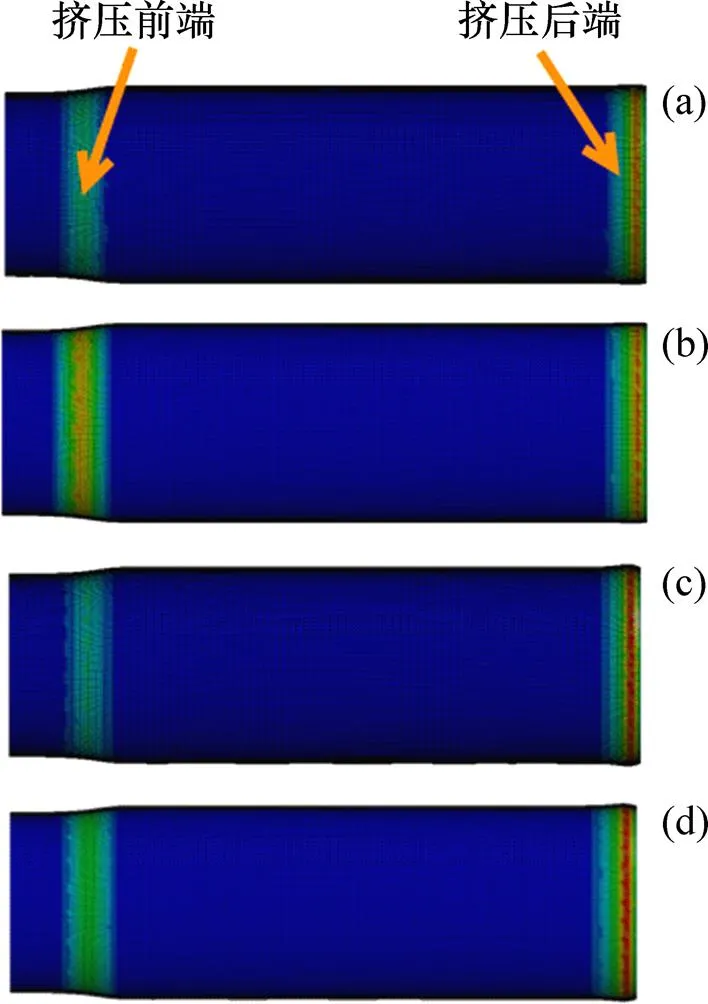
(a) 10 m/s，未考慮應變率；(b) 10 m/s，考慮應變率； (c) 15 m/s，未考慮應變率；(d) 15 m/s，考慮應變率

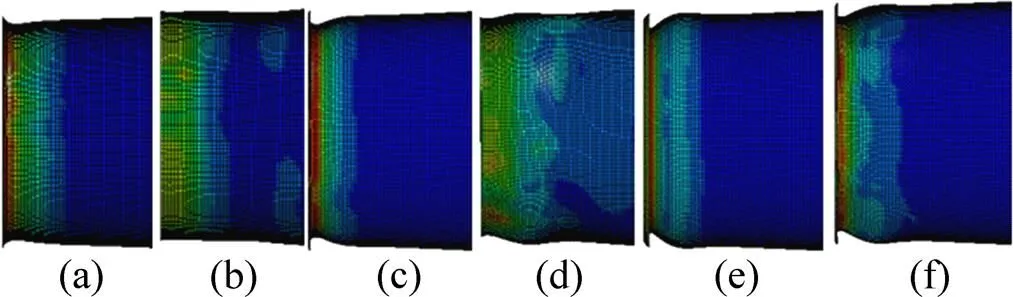
(a) 5 m/s，未考慮應變率；(b) 5 m/s，考慮應變率； (c) 10 m/s，未考慮應變率；(d) 10 m/s，考慮應變率； (e) 15 m/s，未考慮應變率；(f)15 m/s，考慮應變率

壓潰式圓錐管結構前部、中部和后部3單元的應變時間歷程見圖10。從圖10可見：每處單元產生塑性鉸之前即應變明顯增大之前，考慮材料應變率強化效應時單元的應變都比未考慮時的更大，增加的應變即為結構中軸向壓縮變形應變的增加值。材料的應變率強化效應減少了繞塑性鉸轉動變形的應變而增加了軸向壓縮變形的應變，這與前面的分析結果一致。

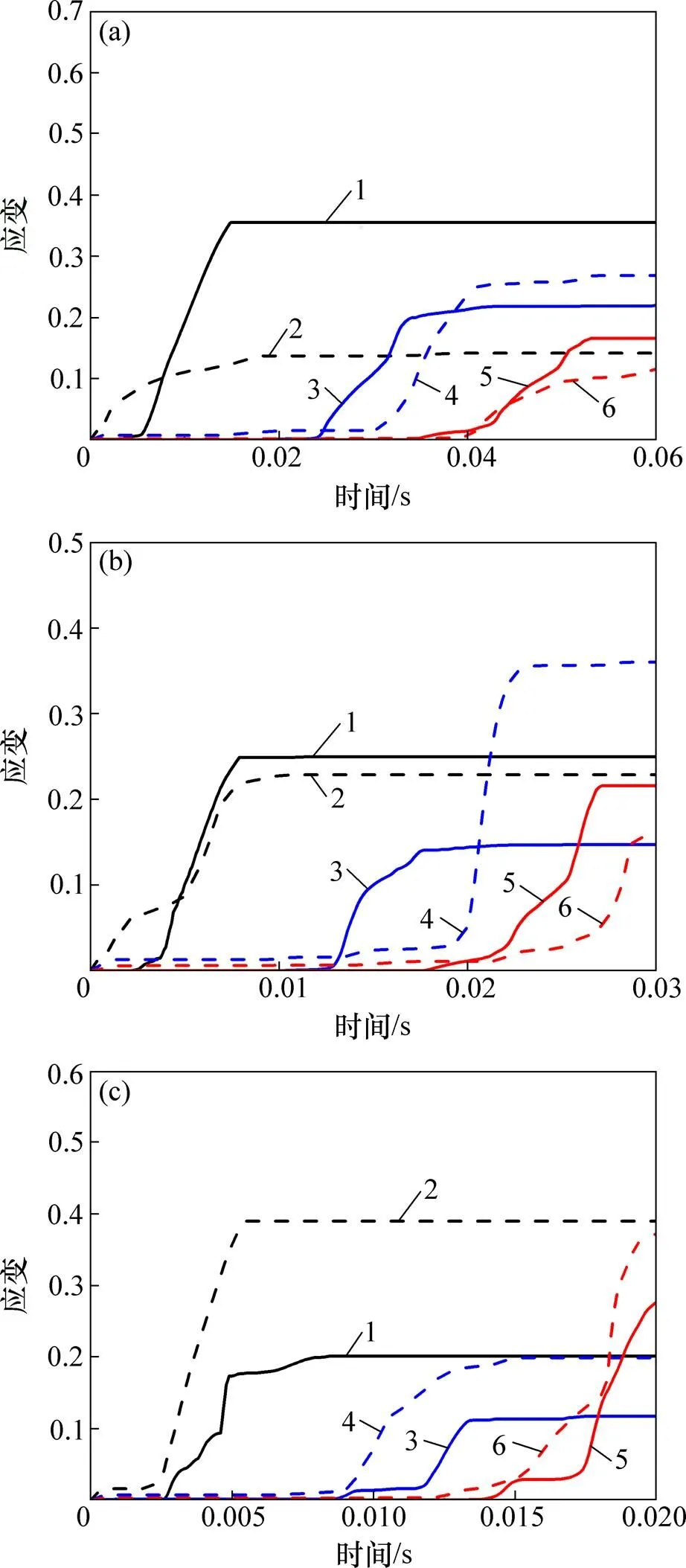
速度/(m·s?1)：(a) 5；(b) 10；(c) 15

4.3 整體變形模式

4.3.1 計算結果

從整體變形模式分析，擠壓式吸能結構變形模式比較穩定，是否考慮材料的應變率效應對結構變形模式影響較小。但隨著沖擊速度增加，在吸能結構遠離法蘭座的擠壓后端會出現圖11中類似于壓潰結構的壓潰鼓脹變形，而且速度越大，壓潰鼓脹變形越明顯。

對于壓潰式圓錐管結構，在不同的沖擊速度下，是否考慮材料應變率強化效應對變形模式影響顯著，如圖12所示。

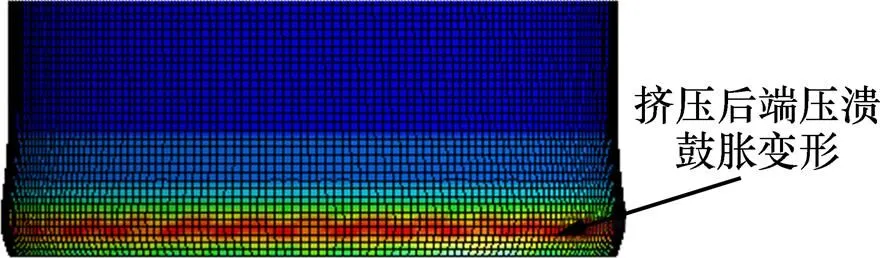
圖11 速度為15 m/s時后端鼓脹變形

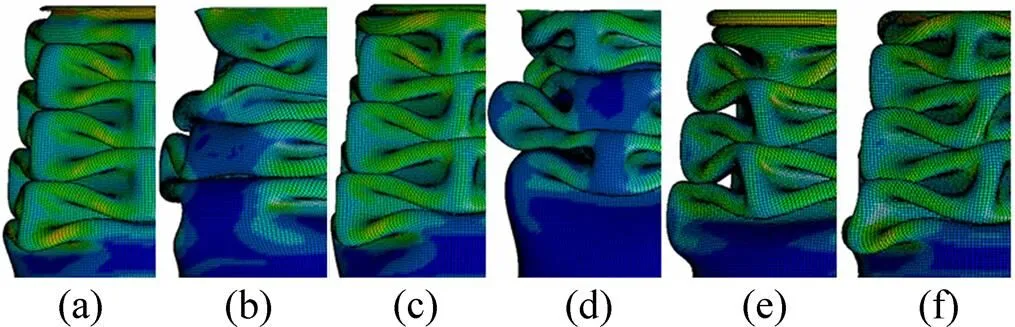
(a) 5 m/s，未考慮應變率；(b) 5 m/s，考慮應變率； (c) 10 m/s，未考慮應變率；(d) 10 m/s，考慮應變率； (e) 15 m/s，未考慮應變率；(f) 15 m/s，考慮應變率

4.3.2 討論與分析

對于擠壓式吸能結構，由于隨速度增加，單位時間內變形增多，靠近法蘭座的擠壓前端的擠壓變形所需要的擠壓力大于擠壓后端壓潰鼓脹變形所需要的壓潰力，故表現為擠壓前端變為瞬時固定端，結構產生擠壓后端瞬時壓潰鼓脹變形。而對于繞塑性鉸轉動的壓潰鼓脹變形，在褶皺完全形成之前，隨著變形增大，壓潰力迅速增大；當壓潰力大于擠壓前端的擠壓力時，開始發生擠壓前端的擠壓變形，并一直以擠壓變形到碰撞結束。

對于壓潰式圓錐管結構，在5 m/s與10 m/s的沖擊速度下，變形模式因考慮材料應變率強化效應由有序變為無序，單個塑性鉸的形成所需要的軸向高度更大，結構出現失穩而未發生屈曲吸能的材料增加。由于考慮了材料的應變率強化效應，材料變形過程中應變率較大的部分材料的流動應力明顯增大。薄壁圓錐管的軸向壓潰變形過程可以用折板的動力學行為進行解釋，主要包括應變率較小的軸向壓縮與應變率較大的繞塑性鉸的轉動。故在考慮材料的應變率強化效應后，繞塑性鉸的轉動變形由于應變率較高，材料流動應力增加顯著，所需要的轉動力矩增大，較大的力矩會繼續向結構后部傳遞，在宏觀上表現為塑性鉸的內折點更接近軸線，即由移動至，圓錐管的直徑內縮現象更明顯，如圖13所示。對于15 m/s的沖擊速度，考慮材料的應變率強化效應時，褶皺形成的時間和位置發生明顯改變，也缺失了第一個階段的圓環變形模式，如圖12(e)和(f)所示。

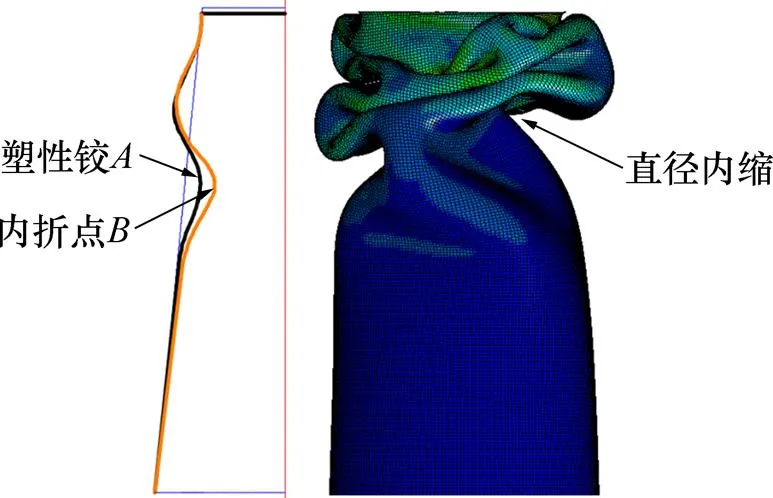
圖13 速度為10 m/s時考慮應變率效應的結構變形

對比2種不同類型的吸能結構可知：圓錐管壓潰式等第二類吸能結構的變形模式受材料應變率強化效應的影響更顯著；擠壓式吸能結構等第一類吸能結構的變形模式與是否考慮材料應變率效應關系不大。在不同吸能結構的變形中，變形形式多樣，包括彎曲、壓縮、拉伸等，各種變形的應變率不同。因考慮材料應變率強化效應，材料流動應力增大，使結構應變率大的變形減少，應變率小的變形增多或者提前發生。

5 誘導式吸能結構

在工程應用中期望吸能結構具有可控的變形模式。對于壓潰式吸能結構，實際碰撞中材料的應變率效應會使結構變形不可控，需要采取一定的誘導措施使材料應變率強化效應增加的應力弱于結構自身的誘導能力，即結構仍然以有序可控的模式變形。故針對前面所研究圓錐管壓潰變形，提出2種不同的誘導方式，并研究在誘導結構下變形模式受材料應變率強化效應的影響。

2種誘導式吸能結構見圖14。

誘導方式1：圓錐管周向間隔90°開設直徑為 20 mm的圓形誘導孔，軸向間距為50 mm。

誘導方式2：錐管管壁預彎變形。

由于速度越大，材料的應變率效應越明顯，變形模式的差異越明顯，故將15 m/s沖擊速度下的2種誘導方式及原有結構的計算結果進行對比。

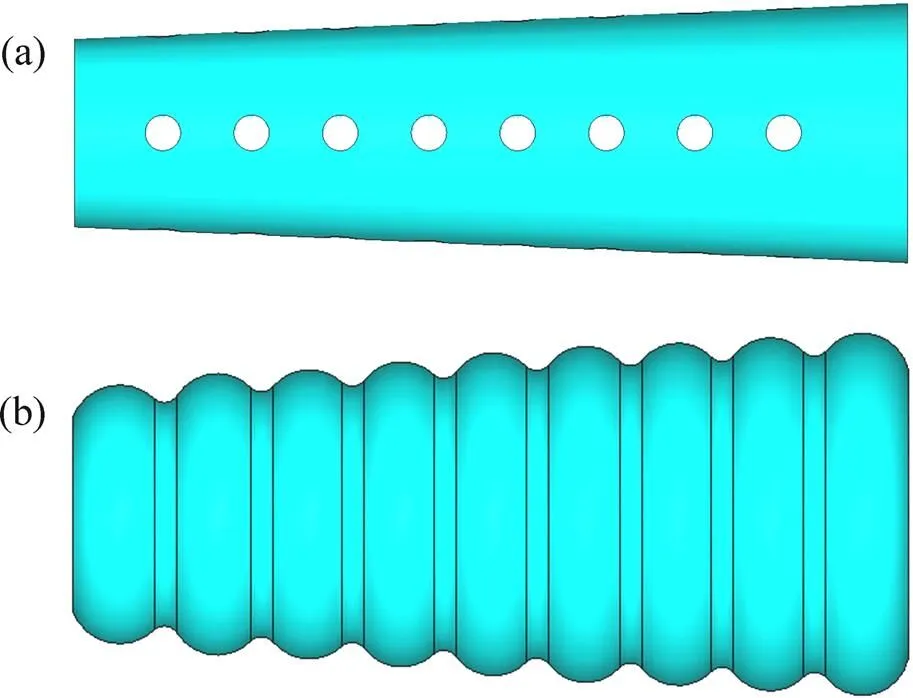
(a) 誘導方式1 ；(b) 誘導方式2

不同誘導方式下壓潰力?位移曲線見圖15。從圖15可見：在誘導方式下，壓潰力?位移曲線近似向上平移，明顯比無誘導結構圓錐管的差異減小，褶皺的數目和出現的位置基本一致。

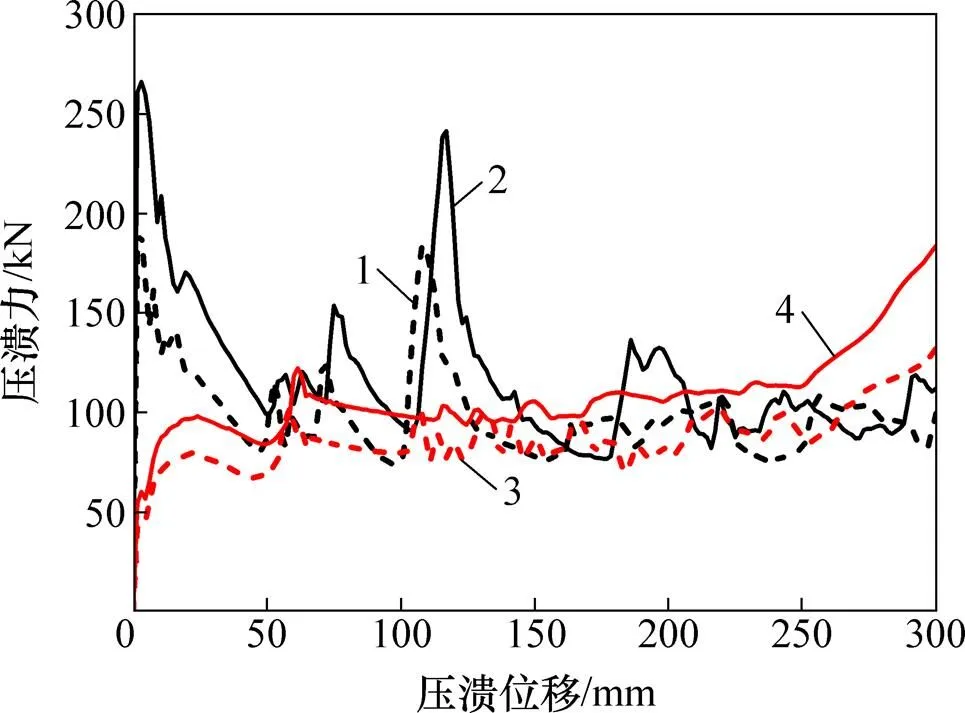
1—誘導孔，未考慮應變率；2—誘導孔，考慮應變率； 3—預彎，未考慮應變率；4—預彎，考慮應變率。

在沖擊速度為15 m/s時，不同結構變形模式見圖16。從圖16可見：在同一時刻，誘導式吸能結構的變形模式受材料應變率強化效應的影響比較小。開誘導孔與預彎變形均相當于人為地約束了褶皺形成的數量和位置。雖然材料應變率效應會使流動應力發生變化，但結構自身的剛度差值大于應變率效應引起的應力差值，結構自身的誘導起主導作用，導致結構變形。對于預彎變形的誘導方式，其變形模式受材料應變率效應的影響最小，因為其誘導方式迎合了結構的變形模式，完成了結構的前期變形，其壓潰力?位移曲線表明其已經近似為第一類吸能結構。

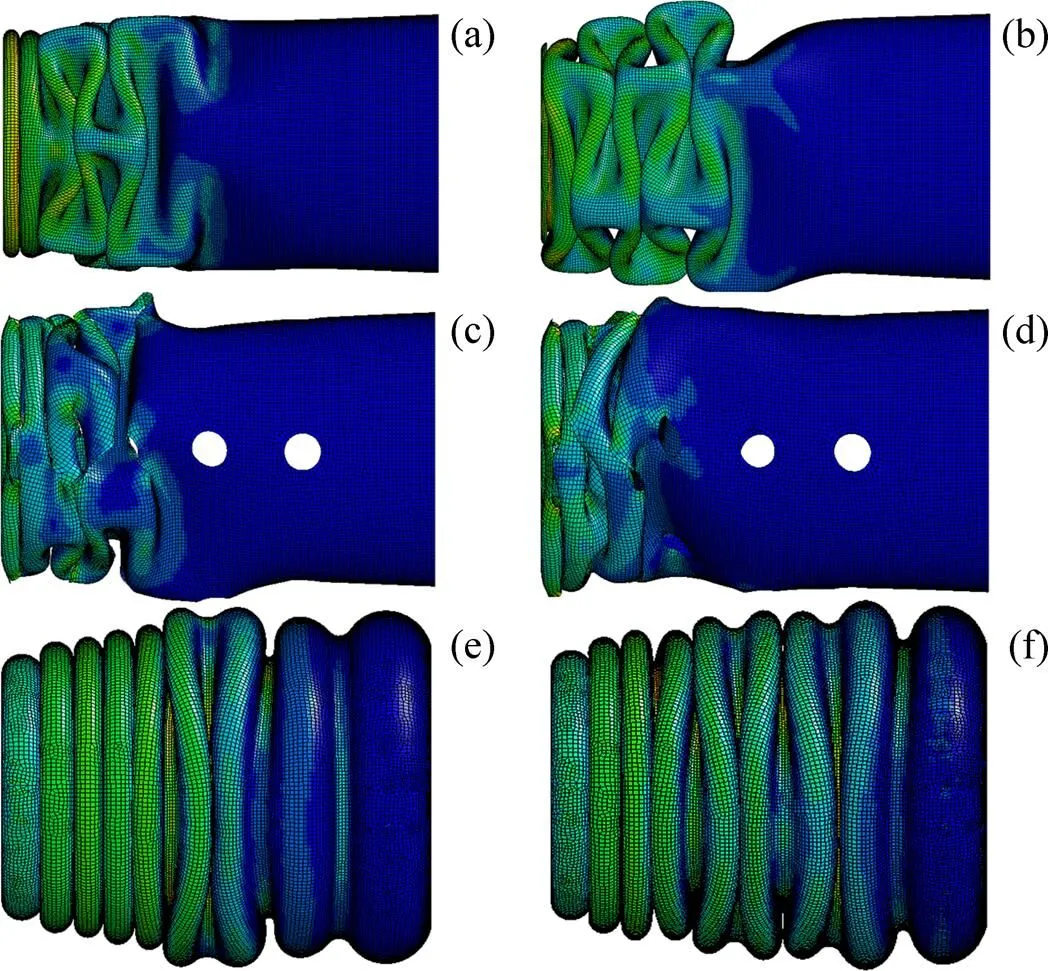
(a) 無誘導吸能結構，15 m/s，未考慮應變率； (b) 無誘導吸能結構，15 m/s，考慮應變率； (c) 誘導孔式吸能結構，15 m/s，未考慮應變率； (d) 誘導孔式吸能結構，15 m/s，考慮應變率； (e) 預彎式吸能結構，15 m/s，未考慮應變率； (f) 預彎式吸能結構，15 m/s，考慮應變率

誘導式吸能結構可以有效減小材料應變率強化效應對結構變形模式的影響，但誘導結構一般是通過預變形或者開誘導孔的方式，預變形因為已有的塑性變形減小了吸能能力，誘導孔則因為材料減少削弱了吸能能力，在設計中需要綜合考慮，對結構進行優化 設計。

6 結論

1) 材料的應變率強化效應會提高結構的承載能力與吸能能力，但不同結構的影響因子不同，這取決于結構的變形模式。材料應變率強化效應對擠壓式吸能結構碰撞載荷和吸能的放大因子比壓潰式圓錐管吸能結構的大，工程中不可忽略該類結構受材料應變率效應的影響。

2) 隨著速度增加，壓潰式圓錐管吸能結構平均應變率和應變率效應放大因子的變化速度比擠壓式吸能結構的大，即壓潰式圓錐管吸能結構平均應變率和應變率效應放大因子對速度變化更敏感。

3) 結構的完整變形和初期變形受材料應變率效應的影響與結構類型相關，對變形中應變率差異不明顯的第一類吸能結構的變形模式影響較小，對應變率差異比較大的第二類吸能結構的變形影響顯著。材料的應變率強化效應會減小應變率大的變形而增加或促進應變率小的變形。

4) 通過誘導方式可以有效減少材料應變率效應對結構變形模式的影響，提高結構變形的有序性和可控性，但在一定程度上減小了結構的吸能能力，在設計時需綜合考慮。

[1] 姚松, 田紅旗. 車輛吸能部件的薄壁結構碰撞研究[J]. 中國鐵道科學, 2001, 22(2): 55?60. YAO Song, TIAN Hongqi. Crash research on thin-shelled structure as vehicle energy-absorbing components[J]. China Railway Science, 2001, 22(2): 55?60.

[2] WOLTER W. 鐵道車輛的防碰撞要求、設計原理和初步結果[J]. 閻鋒, 譯. 國外鐵道車輛, 2004, 41(2): 23?30. WOLTER W. Requirements, design principles and initial results of crashworthy rail vehicles[J]. YAN Feng, trans. Foreign Rolling Stock, 2004, 41(2): 23?30.

[3] KOO J S, KWON T S, CHO H J. 韓國高速列車防撞設計與評估[J]. 周穎, 周艷芳, 譯. 中國鐵道科學, 2004, 25(1): 1?7. KOO J S, KWON T S, CHO H J. Korean high-speed railway anti-impact structure design and appraisal[J]. ZHOU Yin, ZHOU Yanfang, trans. China Railway Science, 2004, 25(1): 1?7.

[4] 謝素超, 田紅旗, 周輝. 耐沖擊地鐵車輛設計及整車碰撞研究[J]. 鐵道科學與工程學報, 2008, 5(5): 65?70. XIE Suchao, TIAN Hongqi, ZHOU Hui. The design of crashworthy subway vehicle and crash research of whole car-body[J]. Journal of Railway Science and Engineering, 2008, 5(5): 65?70.

[5] 李健, 高廣軍, 董海鵬, 等. 帶隔板薄壁方管的耐撞性研究[J]. 中南大學學報(自然科學版), 2014, 45(7): 2481?2488. LI Jian, GAO Guangjun, DONG Haipeng, et al. Research on crashworthiness of thin-walled square tubes with diaphragms[J]. Journal of Central South University(Science and Technology), 2014, 45(7): 2481?2488.

[6] XIE Suchao, ZHOU Hui, LIANG Xifeng, et al. Contrastive analysis and crashworthiness optimization of two composite thin-walled structures[J]. Journal of Central South University, 2014, 21(11): 4386?4394.

[7] 朱濤, 肖守訥, 楊超, 等. 機車車輛被動安全性研究綜述[J]. 鐵道學報, 2017, 39(5): 22?32. ZHU Tao, XIAO Shoune, YANG Chao, et al. State-of-the-art development of passive safety of rolling stocks[J]. Journal of the China Railway Society, 2017, 39(5): 22?32.

[8] 廖其紅, 黃宏成, 薛量. 薄壁鋼結構碰撞性能仿真中材料模型研究[J]. 機械設計與研究, 2001, 17(4): 9, 64?66. LIAO Qihong, HUANG Hongcheng, XUE Liang. On material model for thin-walled sheet metal crashworthiness simulation[J]. Machine Design and Research, 2001, 17(4): 9, 64?66.

[9] 孟廣成, 邰永剛. 材料應變率對護欄碰撞仿真結果影響研究[J]. 公路交通科技(應用技術版), 2012(6): 401?403. MENG Guangcheng, TAI Yonggang. Study on the effect of material strain rate on the simulation result of guardrail collision[J]. Journal of Highway and Transportation Research and Development(Application Technology), 2012(6): 401?403.

[10] 王自力, 顧永寧. 應變率敏感性對船體結構碰撞性能的影響[J]. 上海交通大學學報, 2000, 34(12): 1704?1707. WANG Zili, GU Yongning. Effect of strain-rate sensitivity on the behavior of ship structure in collision[J]. Journal of Shanghai Jiaotong University, 2000, 34(12): 1704?1707.

[11] 曾必強, 胡遠志, 謝書港. 材料應變率強化效應對結構碰撞響應的影響[C]//第八屆國際汽車交通安全學術會議論文集. 蕪湖, 2010: 134?140.ZENG Biqiang, HU Yuanzhi, XIE Shugang. The influences of material strain-rate strengthen effect on the response of structure collision[C]//Proceedings of the 8th International Conference on Vehicle Traffic Safety. Wuhu, China, 2010: 134?140.

[12] 張永康, 張紅兵. 不同構型吸能元件的軸向抗撞擊性能分析[J]. 機械設計與制造, 2011(11): 213?215. ZHANG Yongkang, ZHANG Hongbing. Analysis of axial anti-impact performance for different configuration power-absorbing[J]. Machinery Design & Manufacture, 2011(11): 213?215.

[13] 楊喆, 魏延鵬, 鄒金龍, 等. 薄壁圓筒沖擊屈曲吸能行為的實驗與數值模擬研究[J]. 兵工學報, 2014, 35(S2): 244?250. YANG Zhe, WEI Yanpeng, ZOU Jinlong, et al. Experimental and numerical research on the energy absorption behavior of thin-walled tube under impact load[J]. Acta Armamentarii, 2014, 35(S2): 244?250.

[14] 楊超, 朱濤, 肖守訥. 列車車體鋁合金動態力學性能及其對吸能的影響[J]. 中南大學學報(自然科學版), 2015, 46(7): 2744?2749. YANG Chao, ZHU Tao, XIAO Shoune. Dynamic mechanical properties of aluminum alloy used in car bodies of trains and effect on energy absorption[J]. Journal of Central South University(Science and Technology), 2015, 46(7): 2744?2749.

[15] CALLADINE C R, ENGLISH R W. Strain?rate and inertia effects in the collapse of two types of energy?absorbing structure[J]. International Journal of Mechanical Sciences, 1984, 26(11): 689?701.

[16] 余同希, 盧國興. 材料與結構的能量吸收[M]. 華云龍, 譯. 北京: 化學工業出版社, 2006: 149?152. YU Tongxi, LU Guoxing. Energy absorption of structures and materials[M]. HUA Yunlong, trans. Beijing: Chemical Industry Press, 2006: 149?152.

[17] 許平, 邵恒, 嚴佳麗. 基于自適應響應面法的膨脹式吸能結構耐撞性優化設計[J]. 振動與沖擊, 2017, 36(11): 118?123, 146. XU Ping, SHAO Heng, YAN Jiali. Crashworthiness optimization design of expanding type energy absorption devices based on adaptive response surface method[J]. Journal of Vibration and Shock, 2017, 36(11): 118?123, 146.

[18] 郝林坡, 羅云華, 熊佳霖, 等. 翻卷管吸能啟動載荷的研究[J]. 鍛壓技術, 2015, 40(12): 166?168, 175. HAO Linpo, LUO Yunhua, XIONG Jialin, et al. Research on starting load of inversion tube energy absorber[J]. Forging & Stamping Technology, 2015, 40(12): 166?168, 175.

[19] 洪武, 徐迎, 金豐年, 等. 薄壁圓錐管軸向壓縮吸能特性研究[J]. 振動與沖擊, 2015, 34(5): 88?94. HONG Wu, XU Ying, JIN Fengnian, et al. Energy absorbing characteristics of tapered circular tubes under axial compression[J]. Journal of Vibration and Shock, 2015, 34(5): 88?94.

[20] ABRAMOWICZ W, JONES N. Dynamic axial crushing of circular tubes[J]. International Journal of Impact Engineering, 1984, 2(3): 263?281.

[21] 項燕飛, 楊黎明. 不同管狀和材料對結構能量吸收性能的影響[J]. 寧波大學學報(理工版), 2015, 28(2): 85?90. XIANG Yanfei, YANG Liming. Effects of section and material of tubes on energy absorption[J]. Journal of Ningbo University(Natural Science & Engineering Edition), 2015, 28(2): 85?90.

[22] MAMALIS A G, MANOLAKOS D E, VIEGELAHN G L, et al. The modeling of the progressive extensible plastic collapse of thin-wall shells[J]. International Journal of Mechanical Sciences, 1988, 30(3): 249?261.

[23] MAMALIS A G, MANOLAKOS D E, SAIGAL S, et al. Extensible plastic collapse of thin-wall frusta as energy absorbers[J]. International Journal of Mechanical Sciences, 1986, 28(4): 219?229.

[24] ALMEIDA B P P, ALVES M L, ROSA P A R, et al. Expansion and reduction of thin-walled tubes using a die: experimental and theoretical investigation[J]. International Journal of Machine Tools & Manufacture, 2006, 46(12/13): 1643?1652.

[25] 吳鴻超, 梁增友, 馮陽, 等. 薄壁金屬管在中高速沖擊下的緩沖特性研究[J]. 應用力學學報, 2016, 33(2): 325?331, 377?378. WU Hongchao, LIANG Zengyou, FENG Yang, et al. Study about the cushioning properties of the thin-walled metal tube which working in high-speed impact environment[J]. Chinese Journal of Applied Mechanics, 2016, 33(2): 325?331, 377?378.

(編輯 陳燦華)

Influence of material strain rate effect on crashworthiness of two kinds of energy-absorbing structure

FENG Yue, XIAO Shoune, ZHU Tao, YANG Bing, YANG Haojie

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

The deformation of energy-absorbing structure on rail vehicles is accompanied by obvious strain rate effect. In order to study the influence of material strain rate effect on collision simulation results, the material Q235 which has obvious strain rate effect was studied. Firstly, the reliability of Q235 material model considering strain rate effect was proved by comparison with experimental results and theoretical results. Then the influence of material strain rate effect on the impact load and energy absorption, deformation modes of squeezed and crushed cone energy-absorbing structures were studied. On the basis of this, two kinds of induced energy-absorbing structures were proposed, which were almost not affected by material strain rate effect and the deformation was orderly and controllable. The results show that the influence factor of material strain rate effect varies with different structures. And the influence factor of squeezed structure is larger than crushed cone energy-absorbing structure considering the material strain rate enhancement effect. For different structures, the influence factor of material strain rate effect changes with the change of velocity. The influence factor of the squeezed structure does not increase as greatly as crushed cone energy-absorbing structure when velocity increases. The material strain rate effect has significant influence on the deformation mode of the second type of energy-absorbing structure, and the strain rate enhancement effect reduces the deformation with high strain rate and increases the deformation with low strain rate. The deformation mode of induced energy-absorbing structure is almost not affected by material strain rate effect, and the deformation is orderly and controllable. It can be considered in the engineering design to reduce the influence of material strain rate on the deformation mode.

rail vehicles; crash worthiness; energy-absorbing structure; strain rate effect

10.11817/j.issn.1672?7207.2018.10.032

O313.4；U270.2

A

1672?7207(2018)10?2625?11

2017?11?12；

2018?01?18

國家自然科學基金資助項目(51675446)；國家重點研發計劃項目(2016YFB1200403)(Project(51675446) supported by the National Natural Science Foundation of China; Project(2016YFB1200403) supported by the National Key Research and Development Program of China)

朱濤，博士，副研究員，從事機車車輛設計與理論研究；E-mail：zhutao034@swjtu.cn