粒子群優化-協同克里金法在確定山地斜坡土層厚度中的應用

王桂林，向林川，孫帆

(重慶大學 a.山地城鎮建設與新技術教育部重點實驗室；b.土木工程學院, 重慶 400045)

隨著中國城鎮化進程的不斷推進，為了更有效地保護優質耕地，國土資源部提出了開展低丘緩坡等未利用土地開發試點的工作。殘坡積土是低丘緩坡重要的組成部分，高質量的殘坡積土層厚度信息在土地資源管理、工程建設、地質災害預警預報等方面具都有重要意義。獲取比較精確的土層厚度數據的方法之一是布設高密度的鉆孔,但由于受到經濟水平、技術手段和地形條件的限制,鉆孔點的數量是一定的，這為確定土層厚度帶來了較大的誤差。隨著地統計學理論在工程界不斷應用，空間插值的方法也日益成為解決上述問題的經典方法。將利用統計學與地理信息系統相結合的方法,基于已知鉆孔點的觀測數據進行空間插值來獲得估計點的土層厚度。

空間插值是利用已知的部分空間樣本信息,對未知地理空間的特征屬性值進行估計,是地理信息系統的重要功能模塊之一[1],并在礦業、水文、氣候預報、農業等領域有著廣泛的應用。目前已發展了較多的空間插值方法：如泰森多邊形法[2]、克里金(Kriging)插值法[3]、反距離加權平均法[4]、趨勢面分析法[5]、多項式回歸法[6]等。但這些方法只是局限于已知點的單一屬性值，沒有考慮到其他因素對待估計點屬性值的影響(如高程對土層厚度的影響等)。

基于上述方法在估計空間屬性值時對變量考慮的單一性，學者提出了一種能考慮多個相關變量互相影響的協同克里金法。Yates等[7]將裸土表面溫度和土壤沙粒含量作為協變量，利用協同克里金法(Co-Kriging)估計質量含水率；Ghadermazi 等[8]利用pH值作為輔助變量，估計了飲用水中硝酸鹽的含量。胡丹桂等[9]用考慮降雨量的協克里金法來研究空氣的濕度的空間變化；許晶玉等[10]用考慮土壤粗砂含量和全氮含量的協克里金法來研究山東省種植區地下水硝態氮污染空間變異及分布規律；杜文鳳等[11]將地震數據引入協克里金法中估計煤層厚度的分布規律；黃大年等[12]首次將重力梯度引入協克里金法中來研究巖脈傾向的問題。

半變異函數是克里金法中反映區域化變量空間變化特征的有效數學模型,由其確定擬合模型參數直接影響插值精度。嚴華雯等[13]通過利用加權最小二乘法優化遺傳算法中的適度函數，改進普通基于遺傳算法優化的克里金插值方法；張強等[14]采用基于線性遞減權值的粒子群算法估計半變異函數參數的方法，提高了插值的精度；賈雨等[15]將約束粒子群優化算法用于克里金的插值研究，結果表明能獲得較好的插值精度。

本文采用粒子群優化算法與協同克里金法相結合的方法對土層厚度的空間插值進行研究，并對插值結果進行對比，以期提高土層厚度插值分布的精度。

1 方法原理

1.1 普通克里金插值法

克里金插值法又稱空間自協方差最佳插值法，是以南非礦業工程師D．G．Krige的名字命名的一種最優內插法。該方法首先考慮的是空間屬性在空間位置上的變異分布，確定對一個待插點值有影響的距離范圍，然后用此范圍內的采樣點來估計待插點的屬性值。該方法考慮了已知信息與待估計點相互間的空間結構特性。為達到線性、無偏和最小估計方差的估計，而對每一個樣品賦予一定的權重，最后進行加權平均來估計待預測點屬性值的一種方法。

在克里金法中，用來衡量各個樣本點之間空間相關程度的是半變異函數

(1)

式中：h為兩點之間距離；N是由h分開的成對樣本點的數量；Z是點的屬性值。

一種典型的半變異函數圖像如圖1所示，半變異值隨距離增大而增大，其中有兩個非常重要的點：間距為0時的點以及函數趨于平穩時的拐點，前者表示的是兩個非常接近的樣本點之間的誤差及空間變異，后者表示兩樣本點超過此間離后將不存在空間相關性。

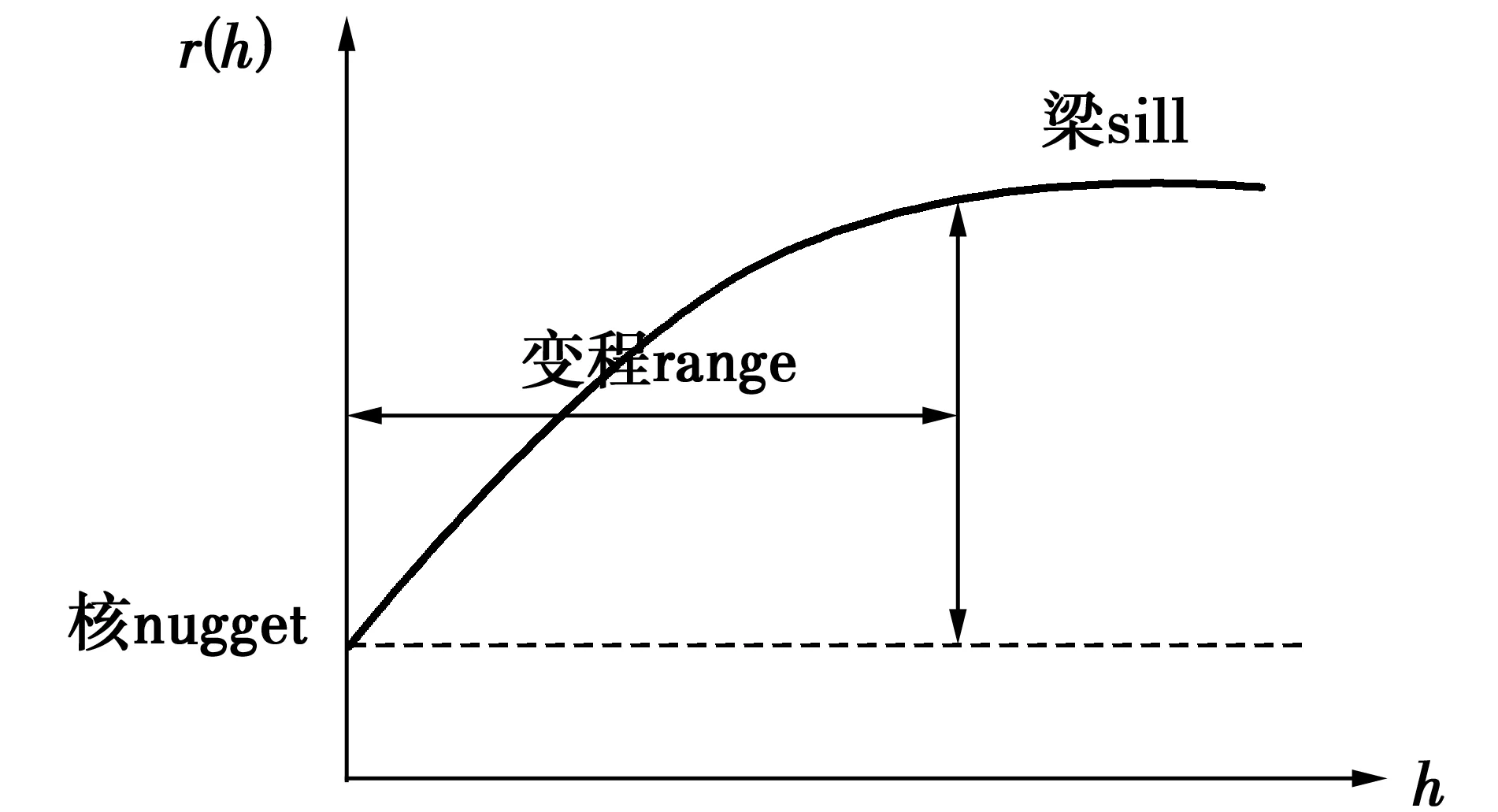
圖1 半變異函數圖

通過式(1)確定半變異函數云圖，然后再擬合出相應的模型表達式，應用式(2)確定內插所需要的權重，并通過式(3)進行未知樣本點屬性值的估計。

(2)

(3)

式中：λi為待定的權重；u為拉格朗日乘子；r(hij)為xi與xj兩點的半變異函數；N為樣本點數量；x0為待插值點，Z為其屬性值。

1.2 協同克里金法

協同克里金插值法可以利用同一變量在不同時空或不同變量在同一時空上的協同區域化性質，用易于測定的變量來對那些難以測定的屬性或變量進行估值，或者用樣品多的變量對樣品少的變量進行估值；如果兩種以及多種屬性具有顯著的空間相關性，則可以優先考慮協同克里金插值法。

在協同克里金法中，γ11、γ22分別表示變量1與變量2的半變異模型函數，其計算方法與普通克里金插值法中的半方差計算方法相同；γ12為協半變異函數，是用來衡量兩個變量各個樣本點之間空間相關程度的表達式

[Z2(xi)-Z2(xi+h)]

(4)

式中：h為兩點之間距離；N是由h分開的成對樣本點的數量;Z1是點關于變量1屬性值；Z2是點關于變量2屬性值。

擬合后用式(5)即可確定空間插值所需要的權重，并通過式(6)進行未知樣本點屬性值的估計。

(5)

(6)

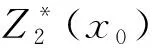
1.3 粒子群優化算法

粒子群優化算法(PSO)是一種進化演變技術，最早是由美國的心理學研究者 Kennedy博士和從事計算智能研究的Eberhart博士受到人工生命的研究結果啟發于 1995 年提出的一種基于群智能的優化算法[16-17]。

粒子群算法的實質是一種信息共享，粒子根據自身的個體最優信息及群體的最優信息不斷更新自己的速度和位置，最后收斂于全局最優解。每個粒子都有一個有待優化問題所決定的適應度值用來評價該粒子的優良程度，一個粒子還有一個速度用于決定它的運動距離即速度，粒子根據自身的運動經驗和群體中其它粒子的運動經驗來調整自己的運動。粒子從此時刻運動到下一時刻的速度由式(7)確定，位置由式(8)計算得到。具體流程見圖2。

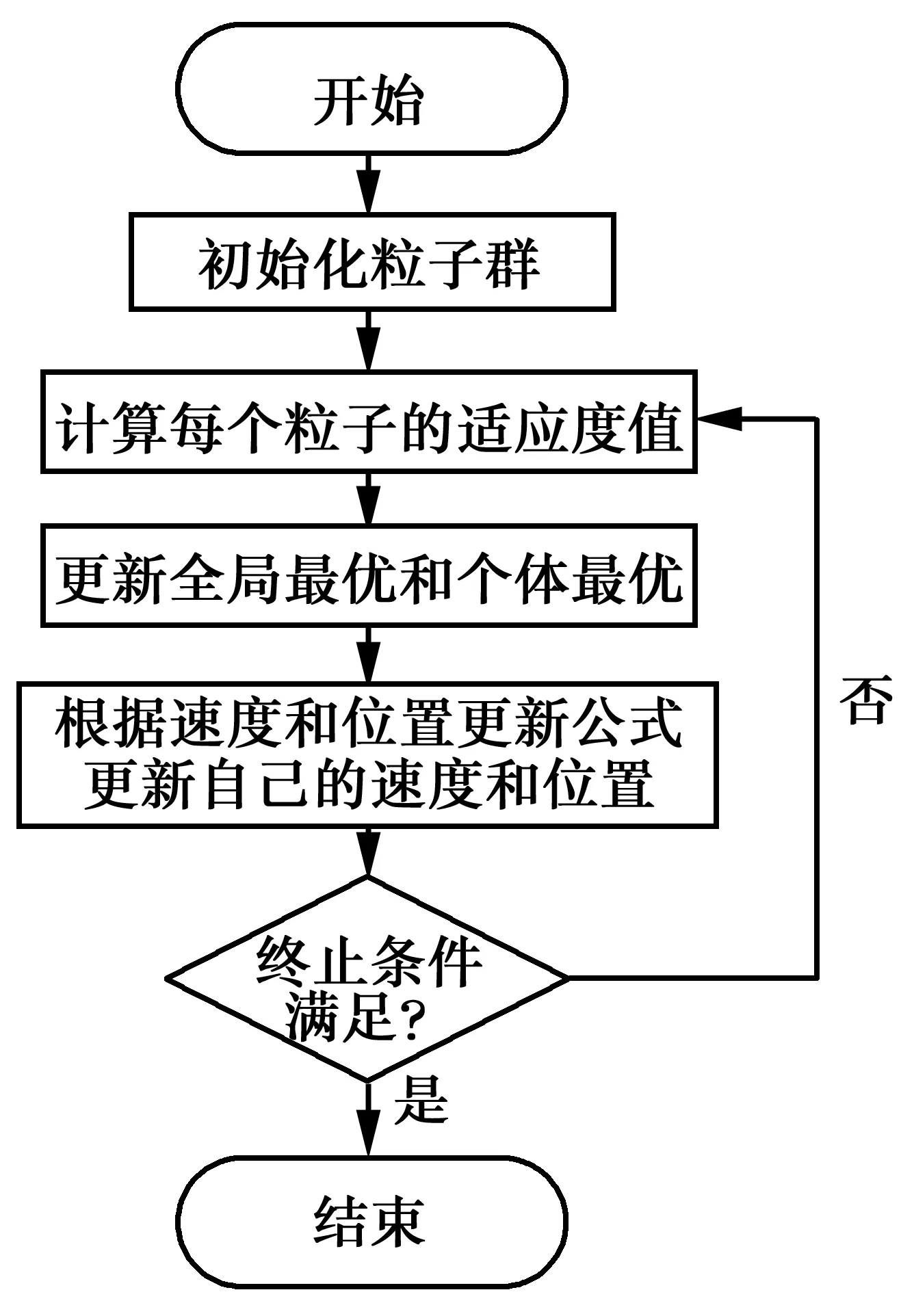
圖2 粒子群優化算法流程圖Fig.2 The flow chart of particle swarm

(7)

xij(t+1)=xij(t)+vij(t+1)

(8)

式中：i為第i個粒子，j為第j個維度；t為更新次數；v為粒子速度，x為粒子位置；r1、r2為0到1均勻分布的隨機數；xpbest粒子自身最好位置，xgbest全局最好位置；ω為慣性權重值。

1.4 基于粒子群優化算法的克里金插值法

擬合半變異函數的模型有很多種，但無論是哪種擬合模型，都涉及到3個擬合參數，分別是圖1中的核(nugget)、變程(range)和梁(sill)。在通常情況下，無論是普通克里金法還是協同克里金法，在確定上述3個參數時用的均為最小二乘法，即在滿足方差最小的條件下得到的，這就會使得3個參數存在較大的誤差。利用粒子群優化算法能快速尋找到全局最優解的特點，將該優化算法應用到確定半變異模型3個參數上。其中該優化算法中的適應度函數為插值結果的均方根誤差。

同時，大量研究表明， PSO算法易陷入局部最優和早熟收斂等缺陷。采用一種基于高斯變異的方法來提高種群的多樣性[15]。在算法出現過早收斂時，能夠使粒子在其他區域進行搜索，跳出局部最優，尋找更優的解。即在迭代到一半次數后，開始對粒子進行變異，對每個粒子進行高斯變異[18]。公式為

xd=gbest(d)×(0.5+σ)

(9)

式中：gbest(d)為全局最優在d維的值；σ為高斯白噪聲。

1.5 預測精度評價方法

為了能夠對上述方法的空間插值精度進行比較,使各方法間的結果更具有可比性,可通過計算鉆孔點的勘察數據與預測數據的誤差來評估各種方法的優劣[19]。均方根誤差(RMSE)可以用來評價預測值和真實值之間的接近程度。利用協同克里金法與普通克里金的均方根誤差減少的百分數(RRMSE)來表示預測精度的提高程度。

(10)

(11)

式中：Z(xi)與Z*(xi)分別為xi處的勘察值與估計值；N為樣本數量。

2 工程實例

2.1 研究區域概況與數據處理

2.1.1 研究區域概況 試驗區位于重慶萬盛經濟開發區，地貌單元為丘陵斜坡地貌；總體趨勢為西側高，東側低；地表總體坡度2°～34°。上圖中的紅色部分為鉆孔點的位置，已知數據有勘察區的平面圖、剖面圖及鉆孔柱狀圖。試驗區最高海拔為418.23 m，最低海拔為334.77 m；共有124個鉆孔點。具體情況見圖3。

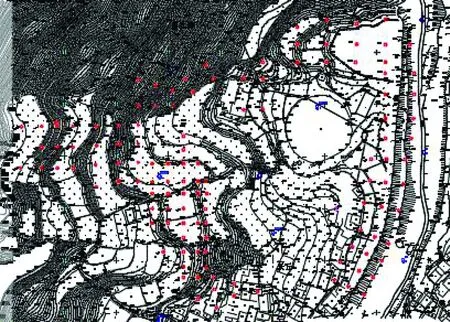
圖3 試驗區鉆孔分布圖Fig.3 The distribution of

2.1.2 鉆孔點數據處理與分析 對試驗區124個鉆孔的高程數據和土層厚度分析，結果顯示：土層厚度和鉆孔點的高程有一定的規律(為了便于與土層厚度比較，高程基準點設為320 m)，具體表現為:在一定的高程范圍內，鉆孔的土層厚度大致和高程值成正相關(見圖4)。

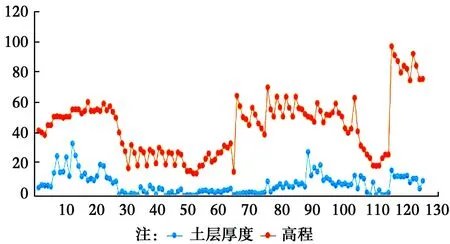
圖4 土層厚度和高程關系圖Fig.4 The correlation between soil thickness and

協同克里金法中，作為輔助變量的前提條件是該變量與待估計變量之間存在著相關性。用SPSS統計軟件中的數據分析功能得到高程值和土層厚度的相關系數為0.552，且在0.01的顯著性水平的條件下，相關性程度為顯著性相關(表1)。因此，可將高程值作為提高土層厚度插值精度的輔助變量。

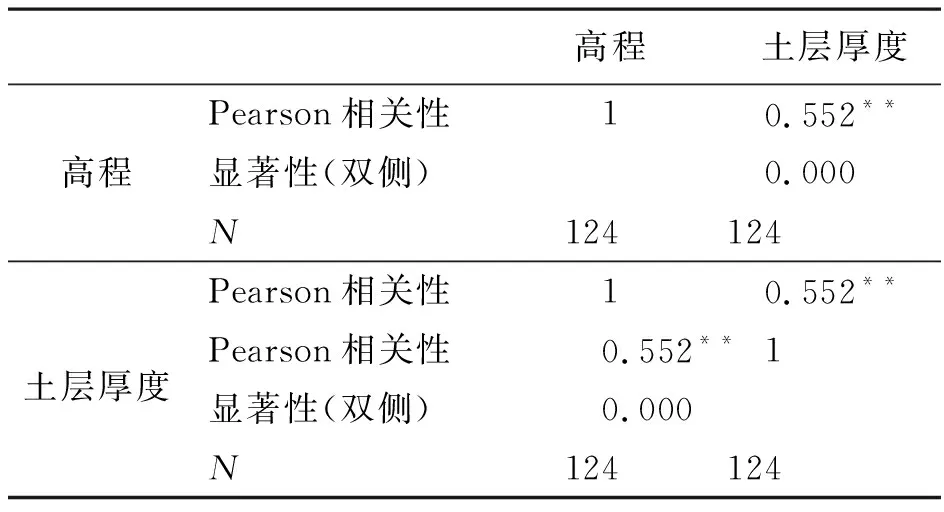
表1 SPSS統計軟件計算結果Table 1 The result calculated by SPSS statistical software

注：**水平(雙側)上顯著相關。

2.2 空間插值模型試驗

采用交叉驗證的方法[20]來估計土層厚度，并用數理統計的方法來比較不同估計模型的估值精度，即首先將待預測點的屬性值Z(xi)暫時剔除，然后將最小二乘法得到的半變異函數表達式用于普通克里金法和考慮高程的協同克里金法來預測Z(xi)的值。結合相應的公式并利用MATLAB編制程序求出拉克朗日系數和待估計點的影響范圍內的各個鉆孔點的權重系數，最后利用式(3)與式(6)分別求出待估計點的屬性值Z*(xi)。重復以上過程直到對所有的124個觀測點進行估計。

基于粒子群優化算法的克里金插值法與基于最小二乘法的克里金插值法區別在于：粒子群優化算法中的半變異模型中的3個參數是未知的；隨機的給每個粒子賦值，這樣每一個粒子就對應了一個半變異函數的模型；然后將每個粒子所對應的半變異函數模型，帶入用MATLAB編制的相應插值程序中，求出均方根誤差，并且將該均方根誤差作為該粒子的適應度函數的適應值。當循環結束后，最小的適應度值的粒子即為所求。進而求出了半變異函數的表達式。

無論是哪一種方法,每一個鉆孔點可以得到真實值和估計值兩類數據。將各個插值方法得到的插值結果與真實值做成火柴棍圖，見圖5～圖8。

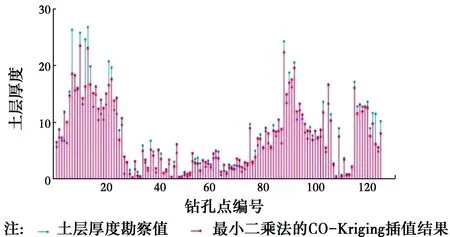
圖5 最小二乘法的O-Kriging插值結果與真實土層厚度Fig.5 O-Kriging based on the least squares method interpolation results and the true soil

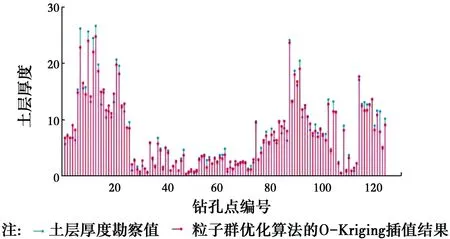
圖6 粒子群優化算法的O-Kriging插值結果與真實土層厚度Fig.6 O-Kriging based on PSO method interpolation results and the true soil

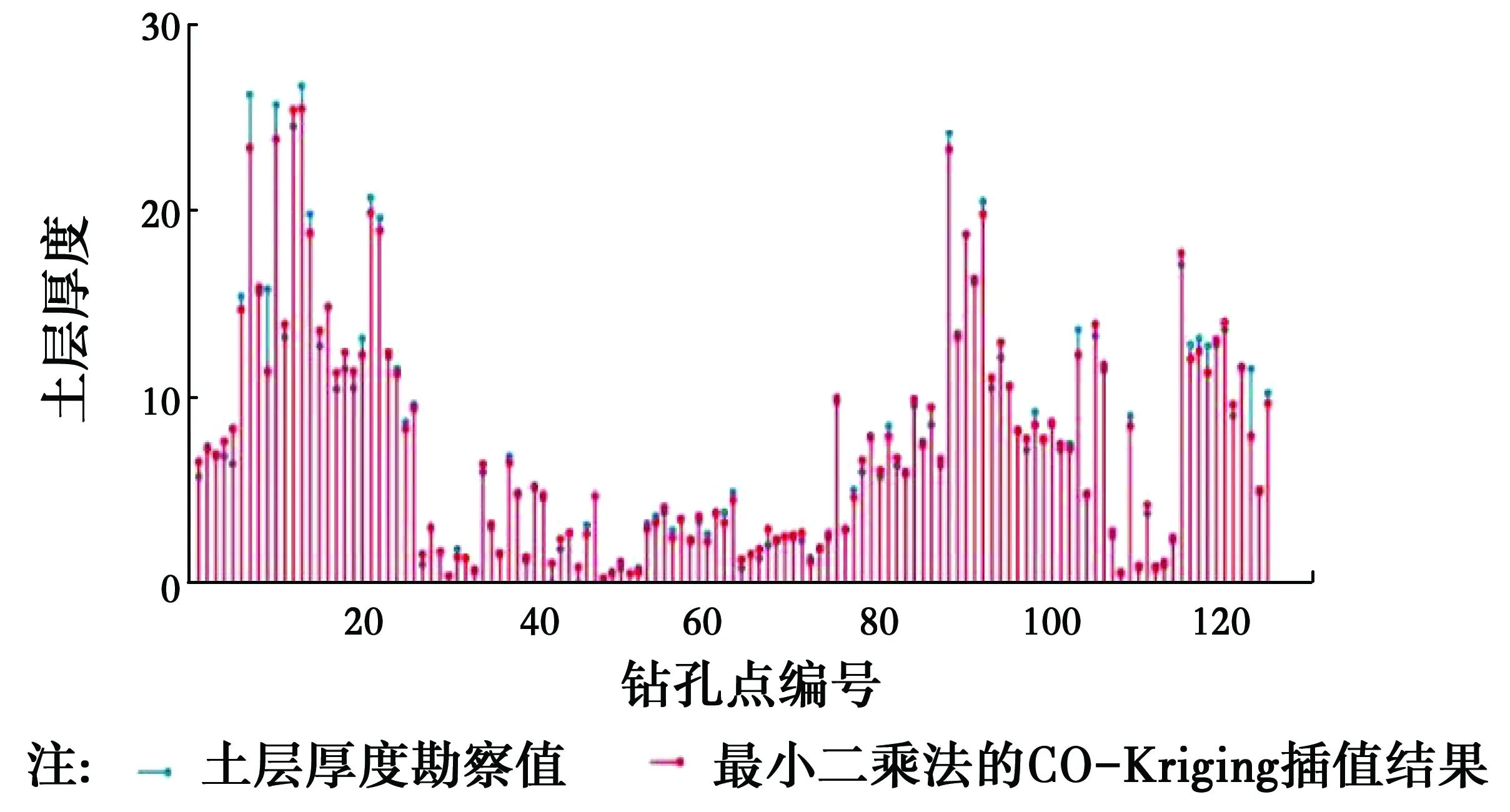
圖7 最小二乘法的CO-Kriging插值結果與真實土層厚度Fig.7 CO-Kriging based on the least squares method interpolation results and the true soil

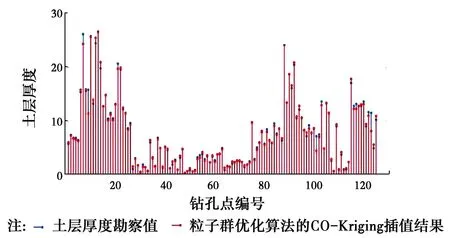
圖8 粒子群優化算法的Co-Kriging插值結果與真實土層厚度Fig.8 Co-Kriging based on PSO method interpolation results and the true soil

從圖5～圖8中可以看出，在上述的4類方法中，基于最小二乘法的普通克里金插值法與勘察值之間的誤差是最大的；而考慮高程的協同克里金法的插值的精度要高于基于粒子群優化算法的普通克里金法；基于粒子群優化算法的協同克里金插值法的精度在4類方法中是最高的，除了極個別的土層厚度較厚的鉆孔點外，其他鉆孔點均與實際情況吻合得較好。

用數理統計的方法來比較4種插值結果的精度的提高程度。其結果見表2。

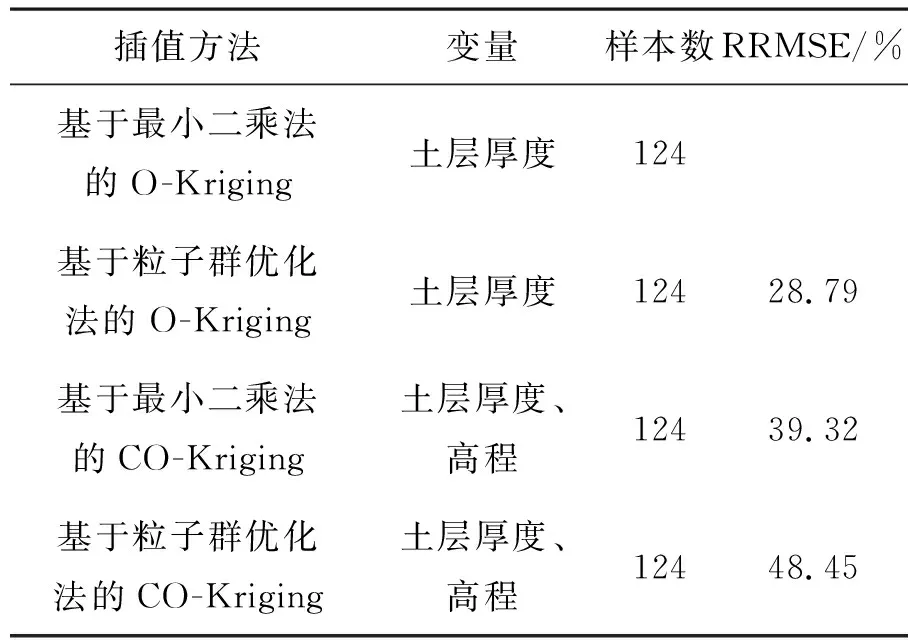
表2 O-Kriging與Co-Kriging預測精度的比較Table 2 Error analysis of O-Kriging and Co-Kriging

從表2可以看出，當采用普通克里金插值法對邊坡的土層厚度進行空間插值時，基于粒子群優化算法的普通克里金插值法較基于最小二乘法的普通克里金插值法的均方根誤差減少了28.79%；當均采用最小二乘法去擬合半變異函數時；協同克里金法的均方根誤差較普通克里金法減少了39.32%；當都采用PSO法去擬合模型參數時；協同克里金法的均方根誤差較普通克里金法減少了19.66%；同時還可以從表中得出結論：當考率單一因素時，考慮高程的協同克里金法較基于粒子群優化算法的普通克里金插值法的插值精度提高了10.53%。

3 結論

以重慶某坡地為研究對象，利用該區域勘察報告中的124個鉆孔點的勘察數據為試驗樣本，采用交叉驗證的方法分別用普通克里金插值法和考慮高程的協同克里金插值法對土層厚度進行虛擬差值。還對在擬合半變異函數模型參數時存在的誤差進行了研究，用粒子群優化算法擬合半變異函數模型，并對4種不同方法的插值結果進行了對比分析，得到的結論如下：

1)將最小二乘法擬合的半變異函數用于普通克里金法插值時會產生較大誤差。

2)對土層厚度進行克里金插值時，考慮高程的協同克里金法較普通的克里金法的插值精度高。

3)通過交叉驗證表明，粒子群優化算法能在一定程度上提高普通克里金插值法和協同克里金插值法的插值精度。