銹蝕鋼筋混凝土梁的抗剪承載力分析模型

余波，陳冰，劉陽

(廣西大學 土木建筑工程學院；工程防災與結構安全教育部重點實驗室； 廣西防災減災與工程安全重點實驗室，南寧 530004)

受混凝土碳化和氯鹽侵蝕等腐蝕環境作用的影響，在役鋼筋混凝土(RC)結構的梁往往發生鋼筋銹蝕。董衛等[1]通過銹蝕RC梁的四點受彎加載試驗，分析了鋼筋銹蝕對RC梁承載機理的影響，發現銹蝕RC梁的承載機理為梁效應和拱效應的復合體，鋼筋銹損率越高，梁效應向拱效應轉化的程度越高；張夢光等[2]通過外加電流加速箍筋銹蝕，開展了4根銹蝕箍筋RC梁的抗剪性能試驗，發現箍筋銹蝕會降低RC梁的抗剪性能和變形能力。由于影響銹蝕RC梁抗剪性能的因素較多，導致其抗剪承載力分析較為困難。霍艷華[3]在未銹蝕RC梁的抗剪承載力模型基礎上，分別引入經驗影響系數φ和γ′來考慮鋼筋銹蝕對混凝土和箍筋的抗剪承載力貢獻的影響，建立了銹蝕RC梁的抗剪承載力模型；趙羽習等[4]引入經驗影響系數Pv來考慮箍筋銹蝕的影響；李士彬等[5]考慮鋼筋銹蝕對箍筋屈服強度和梁有效抗剪截面積的影響，建立了銹蝕RC梁的抗剪承載力模型，但忽略了鋼筋銹蝕對配筋率、配箍率、臨界斜裂縫傾角等重要因素的影響；余璠璟[6]基于試驗數據擬合分析，確定了鋼筋銹蝕對抗剪承載力的影響系數，但當鋼筋未銹蝕或銹蝕率較低時，該影響系數為負值，與實際情況不符；El-Sayed[7]考慮鋼筋銹蝕引起的梁有效抗剪截面積和箍筋截面積改變對抗剪承載力的影響，但忽略了其他重要因素的影響；盧朝輝等[8]基于歐洲規范的抗剪承載力公式，分別引入了鋼筋銹蝕對箍筋和混凝土承擔剪力的折減系數。綜上所述，現有的銹蝕RC梁的抗剪承載力模型主要是在未銹蝕RC梁的抗剪承載力模型基礎上，通過引入經驗性的鋼筋銹蝕影響系數而建立的，缺乏嚴密的理論推導，且考慮的影響因素不全面，導致計算精度有限。

為此，筆者基于修正壓力場理論，通過理論推導分析，建立了可以綜合考慮鋼筋銹蝕對臨界斜裂縫傾角、梁有效抗剪截面積、配筋率、配箍率等關鍵因素影響的銹蝕RC梁的抗剪承載力模型，并通過與85組試驗數據和現有模型的對比分析，驗證了該模型的計算精度。

1 銹蝕RC梁的抗剪承載力模型

根據修正壓力場理論(MCFT)[9-11]可知，RC梁的抗剪承載力V主要由混凝土和箍筋的抗剪承載力貢獻(分別記為Vc和Vs)組成。

V=Vc+Vs

(1)

由于鋼筋的空間銹蝕分布具有非均勻性，導致其薄弱截面在受力狀態下往往會產生應力集中，從而降低鋼筋的強度。其中，根據鋼筋的截面銹損率ηsv可以確定銹蝕箍筋的名義屈服強度fvyc[12]。

(2)

式中：ηsv=(Av-Avc)/Av，Av和Avc分別為箍筋銹蝕前后的截面積；fvy為箍筋銹蝕前的屈服強度。

鋼筋銹蝕會減小縱筋和箍筋的截面積，從而降低配筋率和配箍率。其中，縱筋和箍筋發生銹蝕后，對應的配筋率ρsc和配箍率ρvc分別為

ρsc=Asc/(bh0)

ρvc=Avc/(bs)

(3)

式中：b為梁的截面寬度；h0為梁的截面有效高度；s為箍筋間距；Asc為縱筋銹蝕后的截面積。

此外，鋼筋銹蝕往往會造成混凝土銹脹開裂或剝落，所以銹蝕RC梁的有效截面寬度bc需要根據ηsv進行修正[13]。

(4)

式中：c為混凝土保護層厚度；dsv為箍筋的直徑。

對于外荷載P作用下發生剪切破壞的RC梁，其斜裂縫分布如圖1所示，從中選取的微元體Ω的應力平衡條件和應力莫爾圓[11]如圖2所示。根據微元體Ω的應力平衡條件可得

fx=ρscfsx-vcotθ+f1

(5)

fy=ρvcfsy-vtanθ+f1

(6)

f2=v(tanθ+cotθ)-f1

(7)

圖1 RC梁的斜裂縫分布Fig.1 Distribution of diagonal crack of RC beam

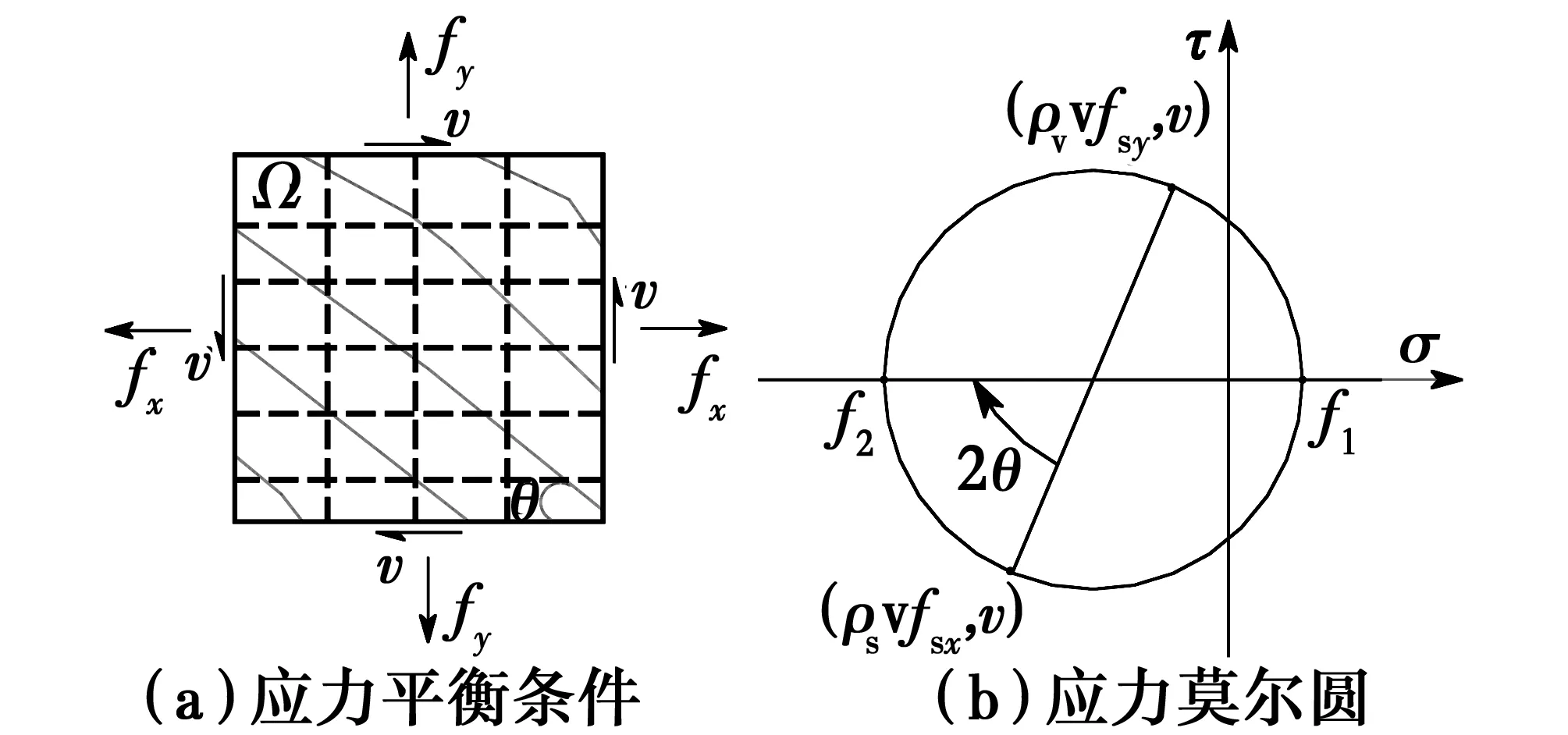
圖2 微元體的應力平衡條件與應力莫爾圓Fig.2 Stress balance condition and stress

(8)

式中：λ為剪跨比；kλ=-0.04λ+1.11,為剪跨比修正系數；knsc=1+(nρsc)-1；knvc=1+(nρvc)-1；n=Es/Ec為鋼筋和混凝土之間的彈性模量比，Es和Ec分別為鋼筋和混凝土的彈性模量；α1=vc/v=Vc/V，建議值為0.38[14]；vc為與混凝土抗剪承載力貢獻值Vc對應的剪應力。由于剪應力v=V/(bchv)，所以可以將式(7)變換為

(9)

由式(9)可知，截面剪應力v由斜拉應力f1和斜壓應力f2抵抗。其中，f1滿足應力-應變關系[9]

(10)

RC梁的受力情況如圖3所示，由豎向力平衡條件可得

Avfvyc=(f2sin2θ-f1cos2θ)bcs

(11)

式中：fvyc為銹蝕箍筋的名義屈服強度。

圖3 RC梁的主應力和力平衡示意圖Fig.3 Principal stress and force balance of RC

(12)

結合式(12)和式(10)可知：抗剪承載力V與f1有關，而f1又與ε1有關。根據MCFT[9-11]進一步分析可知，ε1與斜裂縫間距和θ有關，而θ又與待求的V有關。所以，式(12)通常需要通過迭代分析才能求解。為了避免迭代分析，通過引入ε1與箍筋屈服應變εy的關系來簡化計算[15]。

(13)

結合式(1)、式(10)、式(12)和式(13)，可以建立銹蝕RC梁的抗剪承載力分析模型

(14)

2 對比分析與驗證

(15)

式中：φ和γ′分別為考慮鋼筋銹蝕對混凝土和箍筋抗剪承載力貢獻影響的經驗系數；ρs為未銹蝕縱筋的配筋率。

文獻[4]的銹蝕RC梁抗剪承載力分析模型為

(16)

式中：Pv為考慮箍筋銹蝕影響的經驗修正系數；Cs為混凝土的剪壓區高度；a為剪跨；ρv為未銹蝕箍筋的配箍率。

文獻[5]的銹蝕RC梁抗剪承載力分析模型為

(17)

式中：ft為混凝土的抗拉強度；h0c為RC梁銹蝕后的有效截面高度。

文獻[7]的銹蝕RC梁抗剪承載力分析模型為

(18)

文獻[3-5，7]中的4種模型與本文模型的計算值(記為Vd)的對比分析見表1和圖4。此外，利用式(19)計算各模型的均方根誤差δc。

(18)

式中：Vti和Vpi分別為第i根銹蝕RC梁的抗剪承載力測試值和模型計算值。根據計算結果可知，Vn1、Vn2、Vn3、Vn4和Vd的δc分別為18.77、30.09、45.10、35.63和18.21 kN。由此可見，本文模型的δc最小，說明模型的計算精度更高。

表1 85組試驗數據的設計參數和抗剪承載力測試值Table 1 Design parameters and tested shear strength of 85 sets of experimental data

續表1編號文獻年份nλb/mmh0/mmρs/%ρv/%s/mmfvy/MPaf'c/MPaηss/%ηsv/%Vt/kN抗剪承載力的模型計算值/kNVdVn1Vn2Vn3Vn425[24]2004 7.342.001202001.920.32170.00275.0033.160.0035.2661.0549.2073.7252.0630.0139.2326[28]2011 6.233.001501502.680.19200.00441.5046.1224.8032.7055.4371.6447.1547.2127.1966.6127[24]2004 7.342.001202001.920.32170.00275.0033.160.0024.5660.0063.5076.1268.6630.0141.4928[4]2008 8.472.201501552.260.19150.00331.5224.9119.008.3067.0060.0049.0370.5022.9843.3129[24]2004 7.522.001202001.920.32170.00275.0031.650.0018.7960.1561.8075.7075.8729.5342.1230[28]2011 6.833.001501502.680.19200.00441.5038.295.7221.5055.2084.8363.9356.9326.0063.9431[4]2008 8.472.201501552.260.19150.00331.5224.912.801.7065.0061.4063.3570.5023.2144.2732[24]2004 7.232.001202001.920.32170.00275.0034.160.0030.7763.0548.9175.8659.9030.3240.5633[4]20088.472.201501552.260.19150.00331.5224.918.605.1068.0060.9459.3970.5023.1443.7834[4]20088.472.201501552.260.19150.00331.5224.914.202.7068.0061.3763.1970.5023.1944.1235[4]20088.472.201501552.260.19150.00331.5224.9114.007.2070.0060.5353.9470.5023.0643.4736[4]20088.472.201501552.260.19150.00331.5224.916.604.0069.0061.2661.4770.5023.1643.9437[4]20088.472.201501552.260.19150.00331.5224.9111.606.3072.0060.7256.3670.5023.1043.6038[24]2004 7.522.001202001.920.32170.00275.0031.650.0019.5367.3061.9075.5474.7429.5341.9739[28]20115.972.001501502.680.25150.00441.5050.2424.8025.3071.6987.2069.4091.1137.3653.2140[28]20116.442.001501502.680.25150.00441.5043.1015.8032.1078.0169.2076.3371.3035.7148.9641[4]20088.473.101501552.790.25150.00331.5224.910.001.8080.0072.6662.6159.1523.2357.7642[4]20088.473.101501552.790.25150.00331.5224.910.000.6080.0072.4762.9459.1523.2358.0043[28]2011 6.362.001501502.680.25150.00441.5044.216.3029.5076.3588.6692.2877.3136.2350.0344[23]2010 6.872.001501752.300.25100.00275.0037.893.172.7175.9073.3594.73111.5234.0752.6645[22]2011 8.111.501202002.620.48150.00321.8027.150.0054.1585.2065.4498.6634.0340.3631.7546[23]20106.872.001501752.300.25100.00275.0037.892.442.6177.8073.4494.75111.5234.0852.6847[23]20106.872.201501752.300.25150.00275.0037.893.142.7579.0074.5288.1299.8932.6856.1448[28]2011 6.212.001501502.680.25150.00441.5046.327.7021.3078.1787.6594.4795.6036.7752.8549[23]2010 6.872.201501752.300.25100.00275.0037.893.122.7182.5074.5288.1299.8932.6856.1550[23]2010 6.872.001501752.300.25100.00275.0037.892.041.8583.0073.3794.90111.5234.0952.8251[4]20088.473.101501552.790.25150.00331.5224.910.004.0092.0073.0062.0259.1523.2357.3452[4]20088.473.101501552.790.38254.00331.5224.910.000.7080.0081.6976.1467.5029.6364.2253[4]20088.473.101501552.790.45150.00331.5224.910.000.8076.0086.9183.2172.0133.0773.2554[4]20088.473.101501552.790.38150.00331.5224.910.003.5084.0082.1674.9867.5029.6363.4055[4]20088.473.101501552.790.38203.00331.5224.910.000.4084.0081.6476.2667.5029.6364.3156[4]20088.473.101501552.790.25150.00331.5224.910.002.4096.0072.7562.4559.1523.2357.6557[4]20088.473.101501552.790.45150.00331.5224.910.003.8080.0087.4381.7572.0133.0772.2158[4]20088.473.101501552.790.38254.00331.5224.910.002.2088.0081.9475.5267.5029.6363.7859[23]2010 6.871.801501752.300.25100.00275.0037.893.412.7796.0072.19103.25127.1135.6649.1660[4]20088.473.101501552.790.45150.00331.5224.910.003.8092.0087.4381.7572.0133.0772.2161[4]20088.473.101501552.790.45150.00331.5224.910.003.7092.0087.4181.8072.0133.0772.2462[4]20088.473.101501552.790.45150.00331.5224.910.002.0096.0087.1182.6372.0133.0772.8363[4]2008 8.473.101501552.790.38150.00331.5224.910.004.90104.0082.4074.4167.5029.6362.9964[22]2011 8.111.501202002.620.56150.00463.9027.150.0025.74131.50102.74123.98105.7255.8363.7365[22]2011 8.111.501202002.620.56150.00463.9027.150.0019.54128.10101.38127.46120.9355.8367.6066[22]2011 8.111.501202002.620.56150.00463.9027.150.0011.73129.0099.82131.86140.0955.8372.4867[29]20136.623.002002652.150.20150.00433.0040.8012.1060.10115.40147.01109.5424.0473.49159.0468[29]20136.623.502002652.150.25150.00373.0040.808.1044.30109.80143.48119.4064.3271.81182.4069[29]20136.623.002002652.150.20150.00373.0040.808.6046.50119.80131.89120.9459.0569.02161.88

圖4 抗剪承載力的模型計算值與試驗值的對比Fig.4 Comparison between tested and

結合圖4和表1可知，Vt與Vn1的比值的均值(標準差)為0.95(0.20)，說明Vn1具有一定的計算精度，但是該模型無法揭示銹蝕RC梁的抗剪機理；Vt與Vn2、Vn3和Vn4的比值的均值(標準差)分別為1.16(0.59)、2.27(0.58)和1.32(0.40)，說明這3個模型的計算值總體偏小，且離散性較大，原因在于，上述模型考慮的影響因素不全面且缺乏嚴密的理論基礎；Vt與Vd的比值的均值(標準差)為1.01(0.17)，說明模型的離散性較小，且計算精度較高，主要原因在于該模型是基于修正壓力場理論推導建立的，具有較為嚴密的理論基礎，而且綜合考慮了多種重要因素的影響。

3 結論

基于修正壓力場理論，建立了銹蝕RC梁的抗剪承載力分析模型，并利用85組試驗數據開展了對比驗證分析。分析結果表明：

1)該模型的計算值與試驗值的比值的均值與1.0比較接近，且標準差較小，說明模型的計算精度高、離散性小。

2)銹蝕RC梁的傳統抗剪承載力模型大多屬于經驗模型，考慮的影響因素不全面且缺乏嚴密的理論推導，導致計算精度有限。