“三招”助力數學總復習教學

廣西南寧市武鳴區馬頭鎮馬頭小學玉元教學點(530100)

韋茂林

復習課上，如果教師只是抽取知識點，讓學生被動識記的話，那這樣的識記是模糊的，甚至可能是錯漏百出的。學生不需要這樣生硬的“鋼結構”，而要具有生長力和智能型的“集成電路”。

一、查漏補缺，問題引導，搭建框架

復習不一定要放在學習所有的新知之后，而應趁熱打鐵，立即進行回憶、梳理，因為及時地查漏補缺不僅能為后面學生的分享交流提供依據，而且可以提高復習課的教學效率。

例如，復習“數的認識”之前，教師先讓學生回顧所有學過的數集：(1)數的種類很多，有無數個；(2)數有正負數、奇偶數、合數與質數、分數、整數、小數之分；(3)正數前面可省去“+”號，負數一定要帶“-”號；(4)質數除了1和它本身外沒有其他的因數，合數反之；(5)偶數都可以被2整除，奇數則不行；(6)分數既可以表示具體數量，又可以表示比例；(7)小數和分數可以互化。這是學生自己的復習總結，都是提綱條文，從中可以發現學生腦海中的知識點是分散的，每個新知的出現沒有建立在舊知的基礎上，所以各知識點的層次、從屬關系混亂。于是，教師以問題為導向，進行搭建框架的教學設計。

師：在復習“數的認識”之前，我們先梳理一下以下幾個問題：我們學過的數有哪些？它們之間的關系是什么？如何分類？想辦法把這些內容繪制成圖譜。

(在學生思考回答后，師出示下表)

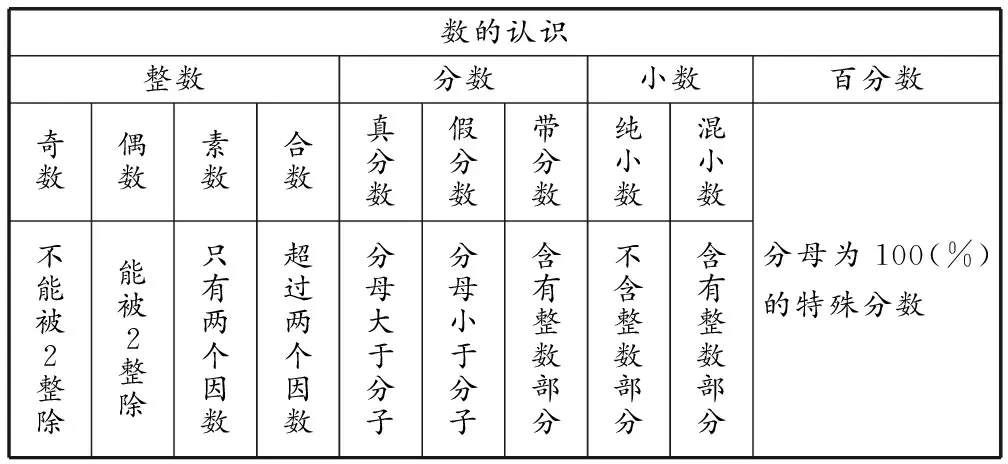
數的認識整數分數小數百分數奇數偶數素數合數真分數假分數帶分數純小數混小數不能被2整除能被2整除只有兩個因數超過兩個因數分母大于分子分母小于分子含有整數部分不含整數部分含有整數部分分母為100(%)的特殊分數

……

上表展現了知識間的內在聯系，使學生真正理解和掌握各個知識點，為后期的交流探討打下基礎。

二、交流優化，深度梳理，內化吸收

復習課上，學生的交流分為兩個層次：第一層次，教師引領學生構圖，感受構建知識框架的優越性；第二層次，提煉方法，讓學生體會到繪制知識圖譜需要掌握全部的知識點。

例如，復習“數的認識”這一單元時，教師以數軸為主線貫穿教學始終：“請在數軸上表示出3、0.30、-3、6這幾個數。”學生要在數軸上表示出這幾個不同形態的數，首先要確定“1”的位置，也就是規劃出單位“1”的長度。如對0.30的定位需要借助分數的意義，即將一個基本長度單位劃分為10份，取其中的3份；對于3與-3的定位，則需要借助數軸的方向性與正負號的指代意義。同時，教師還可以指導學生總結經驗，收集經典例題，使學生在命題、做題、評題的過程中學會從命題者的視角去理解和掌握所學知識。

三、意義遷移，整合統一，凸顯思想

復習課上，教師在引導學生構建知識框架時，既要達到全面、深入、詳細的要求，又要巧妙地整合提煉，做到厚積薄發。如對“能簡便計算要用簡便方法計算”這類題的復習，教師可先引導學生整理出所有的運算律，再尋找其中的相通之處，最后通過整合，使學生高效地掌握所學知識。

關于分配律，既可以是乘法對加數進行分配，又可以是乘法對被減數和減數進行分配，表達式為(a+b)×c=a×c+b×c、(a-b)×c=a×c-b×c，理解為“合并后再擴大相同倍數，可以先擴大相同倍數再合并”。細想減法的性質和除法的性質，表達式為a-b-c=a-(b+c)、a÷b÷c=a÷(b×c)，可以類似地解釋為“分批分次減去(除去)兩個數，可以集中一次性去除”，也可以看成為減法和除法的特殊結合律。

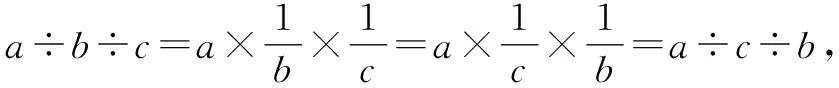
經過運算意義的貫通整合，各種紛雜的運算律就可以統一起來：在只含同一級的混合運算中，均存在交換結合定律；在含有兩級的混合運算中都存在分配現象，即二級運算分配給一級運算。

總之，在將舊知梳理、融會貫通時，更需提煉出更為宏觀的概念——數學思想、數學學習的策略方法，使學生能從更高的層面上掌握所學知識。