Wiener指數與圖的hamiltonian性研究
曾 婷
(湖南城市學院,湖南 益陽 413000)
設G是簡單連通圖,頂點集和邊集分別為V(G)、E(G).在圖 G 中,dG(v)表示頂點 v 的度,dG(u,v)表示G中兩頂點u和v的距離,即為u,v之間最短路的長度.
圖G的Wiener指數[2,4,8],記作W(G),由美國化學家Harold Wiener于1947年提出,定義為W(G)=

一個連通圖中若含有一條Hamilton路,即通過圖中所有頂點的路,則它被稱為可跡圖.若有一個通過所有頂點的Hamilton圈,則稱為Hamilton圖.關于Hamilton圖的存在性,已有許多充分條件,如Dirac條件,Ore條件,Fan條件等等.近來,Hua和Wang 利用哈拉里指數,給出了連通圖變成可跡圖的充分條件.本文將為連通二部圖成為特殊的二部圖即Hamilton圖建立一個新的充分條件.同時得出所有哈密爾頓圖的最大和最小的Wiener指數.
為完成此結論,還需要以下術語.圖G中頂點v的偏心距[5-7]定義為 ecG(v)=max{dG(u,v)|u∈V(G)}.分別將含n個頂點的完全圖、路及圈表示為Kn,Pn,Cn.令Kn,n-1為一個完全二部圖,其中二部集為X,Y,且|X|=n,|Y|=n-1.令為含2n個頂點的二部圖,它是由Kn,n-1圖的X頂點集中的一個頂點與另一個孤立點之間添加一條懸掛邊而得來的.為簡單起見,下文中分別用di,代替dG(vi)和(vi).其他相關標記和術語可參考著作[1].
1 基本引理
推出主要結論之前,先引入一個結果,即給出二部連通圖Hamilton化的一個充分條件.
引理[1]G:=G[X,Y]是頂點數為|X|=|Y|=n≥2,且度序列為(d1,d2,…,d2n)的連通二部圖,這里d1≤d2≤…≤d2n.若不存在小于或等于的整數k,使得dk≤k 和 dn≤n-k,則 G 是 Hamilton 圖.
2 主要結論
下面以Wiener指數的形式,給出一個連通二部圖Hamilton化的新的充分條件.
命題2.1令G:=G{X,Y]是頂點為|X|=|Y|=n≥2的連通二部圖,若
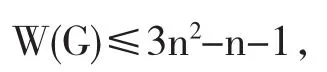
則G是Hamilton圖.
證明假設G不是Hamilton圖,而是一個連通二部圖,其度序列為(d1,d2,…,d2n),且 d1≤d2≤…≤d2n.由引理1.1可知,存在一個,使得 dk≤k和dn≤n-k.可以求得,對G中任意的i(i=1,2,…,2n),有D^i≥di+2(2n-1-di).由(1)式,得到
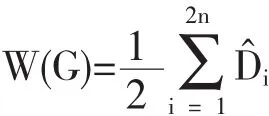

結合這一結論及上述假設,易知W(G)=3n2-n-1.因此,(2)(3)(4)式中所有不等式應變為等式.
由此可知,
(a)由(2)式的等式知,圖G的直徑不超過2.
(b)由(3)式的等式,有 d1=d2=…=dk=k,dk+1=…=dn=n-k及dn+1=…=d2n=n.
(c)由(4)式的等式,有 k=1 或 k=n-1.
因此,可設 k≠n-1,由(c),有 k=1.再根據(b),可推得.但是G中這個唯一的懸掛頂點偏心距為 3,也與(a)矛盾.
綜上,G是Hamilton圖.證畢.
以上通過Wiener指數獲得了Hamilton圖的一個新的充分條件,只要圖的Wiener指數不超過上界而給定一個值,即可推出這個圖是Hamilton圖.那么在所有Hamilton圖中,哪些圖可達到最大或最小Wiener指標?不難知道,從一個圖中移走一條邊,會增加其Wiener指數,又因為此圖為Hamilton圖(即含有Hamilton圈),所以我們得到以下結論:
命題2.2 所有頂點為n的Hamilton圖中,圈Cn和完全圖Kn分別達到最大和最小Wiener指數.
3 結語
從文中看出,只要滿足關于Wiener指數的一定的不等式,就能知道一個連通二部圖能否含有Hamilton圈,這為研究圖的Hamiltonian性提供了方便.最后還得到了所有Hamilton圖的最大最小Wiener指數.

