一種新的直方圖數字水印算法研究與設計

肖文靜 岳 楨 宋培非 李子臣

1(北京印刷學院信息工程學院 北京 102600)2 (北京郵電大學信息安全中心 北京 100876)

圖像直方圖與像素在圖像中位置無關，所以能被很好地應用到抗幾何攻擊的數字水印算法中.當圖像被幾何攻擊時，圖像的大小和空間位置會發生相應的改變，但是直方圖中各個灰度級的像素個數，確切地說是各個灰度級像素個數占總像素個數的比例基本保持不變，即直方圖的形狀特征保持穩定，所以基于直方圖的水印具有較強的魯棒性.

1998—2008年，文獻[1-4]提出了基于直方圖修改的水印算法，但嵌入容量較低，同時在傳統信號處理下其魯棒性不強.2010年，Deng等人[5]在Xiang的工作基礎上從統計區間選取、直方圖修改方式和提取方式幾個方面對算法進行了改進，將原先的2個bin 1組修改為3個bin(灰度級) 1組，增強了水印的魯棒性，但算法并沒有提高水印嵌入容量.2008—2015年，文獻[6-9]給出了一種基于直方圖修改的圖像水印算法，能抵抗一般的傳統信號處理攻擊以及幾何攻擊，增強了算法的魯棒性，同時應用到視頻水印中，但該算法并未對嵌入容量進行改進.

2017年在數字水印國際研討會(Digital Forensics and Watermarking)上，Feng等人[10]提出了2種新的方法來改進嵌入算法：第1種算法執行多輪嵌入，以攜帶更多的水印比特；第2種算法使用1組直方圖嵌入多個水印位，在此基礎上優化系數轉移，以減少嵌入失真.這些算法一定程度上提高了水印信息嵌入量，但花費更多bin的資源，單位圖像資源嵌入水印信息量并未增加.

提高水印嵌入容量、增強魯棒性目前依然是直方圖數字水印算法研究熱點.本文提出一種新的基于2bin直方圖的數字水印算法，分3種情況修改直方圖中相鄰的2bin，嵌入信息由原來的“0,1”組成的字符串變成“-1,0,1”組成的字符串,即從二進制轉為三進制，新的算法提高了嵌入水印的容量，同時增強其魯棒性.實驗結果表明，新的算法嵌入水印信息容量增加60%，并且有較高的魯棒性.

1 基于直方圖數字水印算法

1.1 生成直方圖

首先，對于1張大小為m×n的灰度圖，我們可以通過式(1)提取出直方圖，記為H.直方圖有#(H)個bin.

(1)

1.2 水印嵌入

每2個相鄰的bin組成1組，嵌入1個水印位.假設H(2i-1)和H(2i)這2個bin用于嵌入水印信息M(i)，1≤i≤#(H)2.根據式(2)調整bin的高度.具體如下：

(2)

閾值T控制bin之間的間隙數量，n表示從H(2i)轉移到H(2i-1)的系數的數量.當系數需要從H(2i-1)轉移到H(2i)時，n為負數.它的值可以通過式(3)計算，使轉移系數最小化.

(3)

1.3 水印提取

(4)

上述方案已經在很多方法中擴展.然而，嵌入算法仍然相似.它們同樣面臨水印嵌入容量的問題.下面簡單介紹一種著名的基于直方圖修改水印算法.

2 Xiang的基于直方圖水印算法

2008年，Xiang等人[1]提出的是一種利用直方圖形狀和圖像均值進行水印嵌入的方法.

該算法的思路如圖1所示.

假設2個bin的像素個數分別為a和b，則嵌入規則如下：

(5)

其中T是在圖像質量和魯棒性之間取折中的1個閾值.修改直方圖，本質上是修改圖像中的像素信息.下面舉例說明.

假設有2組bin，像素值分別為110，111和120，121，相應像素值的個數分別為4，5和8，7，我們對其進行水印嵌入,如圖2所示.假如嵌入信息分別為“1”和“0”，對2組bin進行如下調整以滿足嵌入規則.

圖1 Xiang的直方圖水印嵌入方法

圖2 直方圖調整

3 新的基于直方圖水印算法

針對嵌入容量較小的問題，本文提出了一種新的改進直方圖水印算法，增加嵌入水印比特信息.在傳統的算法中，嵌入信息以“0，1”字符串的形式表示，分2種情況完成水印的嵌入和提取.本文提出的算法中嵌入信息是由“-1，0，1”這3個數字組成的字符串，相當于三進制，提取信息時，按照3種情況提取.

3.1 嵌入算法

首先對圖像進行高斯低通濾波，得到其圖像低頻部分，然后對圖像低頻部分，計算其均值并提取圖像直方圖，根據均值選定統計灰度區間，將統計區間每2個灰度級為1組，按照嵌入規則每組嵌入1 b水印信息，像素調整在同一組下的相鄰灰度級之間進行，隨機選取像素.

嵌入規則如下：

(6)

其中T≥1是在圖像質量和魯棒性之間取折中的一個閾值.

1) 嵌入水印比特為0.如果|a-b|≤1，不需要調整任何像素；否則，如果a>b，從bin1的像素中隨機選擇I1個進行調整，使得它們落入bin2內.即調整后a1=a-I1,b1=b+I1，且滿足|a1-b1|≤1；如果b>a，同理.

(7)

(8)

3.2 提取算法

提取算法依照嵌入規則逐個提取.首先對圖像進行濾波，計算均值和直方圖，確定統計區間并進行兩兩分組，依照規則對每組進行水印比特信息提取.

提取算法如下：

2)提取第i組的2個bin嵌入的水印比特；

假設第i組的前后2個bin的像素個數為a′和b′，則第i位水印比特為

(9)

3) 重復步驟2)，提取出所有水印信息.

4 實驗結果

前面已經對本文提出的三進制直方圖數字水印算法進行了介紹，本節將對算法進行相應的魯棒性測試，給出實驗結果并進行分析和討論.

圖3 原始圖像

測試所選測試集為50幅512×512大小的灰度圖像(本文以Lena圖為例)，原始圖像、嵌入水印圖像以及對應直方圖如圖3～5所示：

圖4 嵌入水印圖像

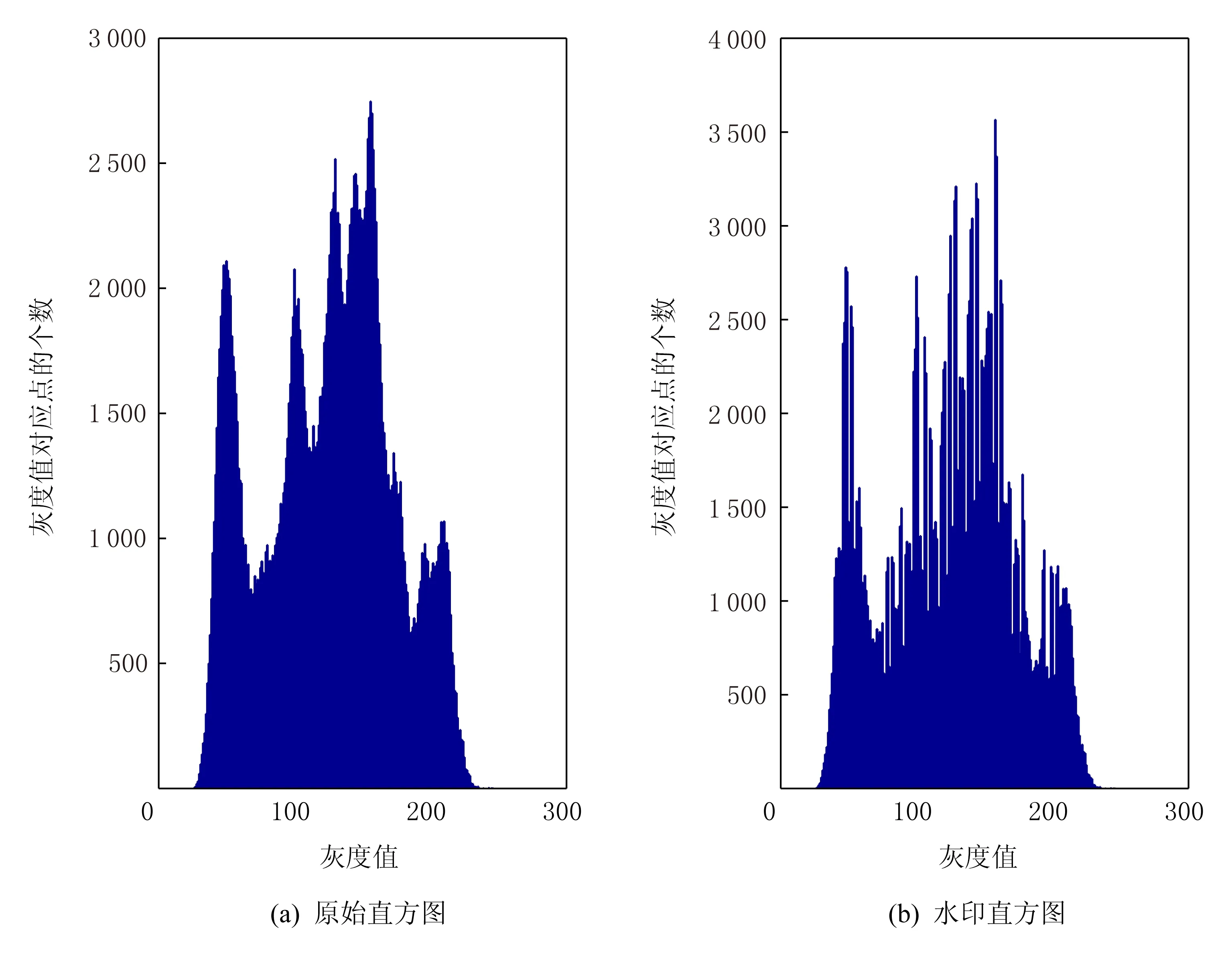
圖5 原始直方圖和嵌入水印直方圖對比

4.1 容 量

水印信息嵌入容量測試.將該算法與文獻[1,10]所提出的算法進行比較.設定2種算法中直方圖bin的數量#(H)增加，以擴大嵌入容量.比較#(M)=32和#(M)=48情況下的所有算法，如表1所示:

表1 算法實驗數據對比

A為直方圖灰度均值；α為嵌入閾值；π為每段中bin的個數.

通過分析表1中的數據可以發現，在嵌入容量一定的情況下，本文算法進行水印嵌入需要更少的bin.由此得出結論，本文提出的算法嵌入容量明顯提高.

4.2 圖像質量測試

圖像質量測試的實驗結果用峰值信噪比(PSNR)來反映,MAX表示最大灰度級，img表示原始圖像，imgn表示嵌入水印圖像，MES表示均方差.計算公式如下，其中B表示編碼一個像素所用二進制位.

MAX=2B-1,

假設B=8,經計算可知PSNR= 51.717 5，該結果滿足對圖像質量的要求.

4.3 魯棒性測試

魯棒性測試主要采用圖像壓縮、旋轉、劃線和剪切4種攻擊方法進行.并與Xiang，Deng，Hu這3人的算法結果進行對比分析.

對水印算法在幾種攻擊下的魯棒性，實驗結果用誤碼率(BER)來反映.

假設水印長度為L，則

其中numerror為提取錯誤的水印的比特位數.

測試內容包括:

圖6 JPEG壓縮攻擊后BER測試

1)圖像壓縮.JPEG壓縮，壓縮系數從10～100，壓縮系數越大，圖像質量越好.測試結果如圖6所示：

2) 旋轉.圖像旋轉角度從3°～30°，間隔為3°.測試結果如圖7所示：

圖7 旋轉攻擊后BER測試

3) 劃線.劃線數量從1～8條.測試結果如圖8所示：

圖8 劃線攻擊后BER測試

4) 剪切.剪切部分所占比例逐漸增大至0.5.測試結果如圖9所示：

圖9 剪切攻擊后BER測試

從實驗結果我們可以看出，本文算法在JPEG壓縮攻擊下提取正確率整體高于Xiang的方法，同時在旋轉攻擊和劃線攻擊下，相比于其他算法，該算法提取正確率較高.同時，本文的算法對傳統信號處理攻擊和幾何攻擊都具有較好的魯棒性.

5 結 論

本文針對圖像直方圖水印嵌入容量較小的問題，對水印嵌入信息進行修改，將水印信息由原本的“0,1”字符串改成“-1，0，1”組成的字符串，即水印信息從二進制變為三進制，并提出了一種新的基于直方圖圖像水印的算法.

實驗結果表明，本文算法在保證嵌入后圖像高質量的同時，在抵抗傳統信號處理攻擊和幾何攻擊方面也有比較好的表現.同時，增加了水印嵌入容量，在進行JPEG壓縮攻擊和旋轉攻擊時，算法提取正確率明顯提高.