信息技術專業數學課程實驗教學設計初探

董 飛， 聶秀山

(1. 山東師范大學 新聞與傳媒學院， 濟南 250014; 2. 山東財經大學 計算機科學與技術學院， 濟南 250014)

0 引 言

隨著現代社會的發展，以計算機軟件、硬件、電子技術、數據庫等為核心的信息技術已經成為推動社會生產力發展的主要動力。另外，AlphaGo在圍棋的人機大賽中取得的巨大成功，也使得人工智能成為產業界和學術界的研究熱點，特別是2017年7月份國務院印發《新一代人工智能發展規劃》，使得人工智能上升為國家戰略。因此，信息技術人才需求量會越來越大，高校作為信息技術人才培養的主要來源，對信息技術類專業(包括計算機科學與技術、網絡工程、數字媒體技術和藝術專業等)知識教學至關重要[1-3]。在信息技術類專業的課程體系中，數學類課程，包括高等數學、線性代數和概率論與數理統計，是信息技術類專業的基礎學科，也是核心課程，對后續專業課程的學習具有舉足輕重的作用。因此，高等數學課程的設置和教學體系對信息技術類專業人才的培養有著重要影響。

高校數學課程不同于高中階段所學的數學[4]，高校數學課程和學生的專業課程有著緊密的聯系，正因如此，數學課程成為高校各專業特別是理工類專業的基礎課程。但是，目前高校數學課程的教學主要是采用傳統的理論教學模式[5]，教師對所有專業的學生“一視同仁”，灌輸大批定義、定理和解題技巧。往往這種模式培養出來的學生更適合參加考試，學生在學完數學課程中，普遍感覺是“數學難，數學很重要”，但是究竟怎么使用，特別是在本專業領域如何使用，仍然比較迷茫。針對這一問題，作者結合近年來的教學經驗，在本文中以信息技術類專業學生為研究對象，以概率論與數理統計這門數學課程為例，探討信息技術類專業中的數學課程實驗教學模式。

1 高等學校數學課程教學現狀

目前，國內高校大部分專業，特別是理工類專業都開設了數學類課程，但是數學課程的教學還是以傳統的課堂理論教學模式為主，學生被動學習，而且教學內容與學生的專業知識聯系不緊密，無法適應人才培養和現代教學培養體系的需要[6-8]。總體來說，目前高等學校數學課程教學存在以下2個問題。

(1) 教學內容單一，與專業知識聯系不緊密。在高校的現行體制內，數學課程的授課教師隊伍一般是由基礎教學部(系)或數學學院的老師組成。不可否認，這些老師大多是數學相關專業出身，對數學知識的研究和理解比較深入，對數學知識的講解也是得心應手，但是這部分授課老師大多對其他專業的了解有限。另外，數學授課老師的教學活動、課程建設也一般局限在本系部內進行，與其他各專業的交流也比較少。這些現象導致的問題就是，任課老師對所有專業數學課程的教學幾乎千篇一律，使得學生所學的數學知識與專業知識關聯不大。而數學知識與專業知識的關聯對于學生專業能力的培養又至關重要。大部分學生又無法通過自學，把數學知識和專業知識有機結合起來。這就使得通過當前高校數學課程的教學培養出來的學生更適合于進行考試，而不是對知識的靈活應用，特別是在專業領域的應用。

(2) 理論教學多，實際動手機會少。數學類課程是一類理論性較強的課程，而傳統的數學教學模式往往也是更注重于理論的教學，授課教師在課堂上會花費大量的時間講解定義、定理證明以及解題技巧。不可否認，這些定義和定理的證明對學生理解知識點具有重要的幫助。但是傳統的教學模式忽視了對學生實踐能力和創新研究能力的培養[9]，學生僅僅會用定理、公式解題，而不能利用定理、公式對實際問題，特別是專業領域的問題進行建模、邏輯推理和解決問題。令人欣慰的是，隨著近年來數學建模比賽的流行和普及，上述問題得到一定程度的緩解，但是，數學建模畢竟是少數學生參加的活動，在平時教學中注重實踐教學，是數學課程教學需要關注的問題[10-12]。

基于以上兩個方面，以信息技術類專業為對象，以概率論與數理統計課程為例，探索高校數學課程的實驗教學設計模式。

2 信息技術類專業數學課程實驗教學模式

信息技術類專業教學課程實驗教學模式如圖1所示，共有3層構成，第1層主要是課程基礎理論知識學習，第2層是實驗類型模塊，第3層是實驗創新能力提升。在此模式中，目前的課程教學主要集中在第1層，對第2和第3層涉及較少，本文針對第2和第3層進行詳細分析。

圖1 實驗教學模式

2.1 實驗類型

本文提出的實驗教學模式中，依據對學生能力的培養和與專業知識結合的原則，設計了2類實驗：

(1) 設計型實驗。設計型實驗主要是針對具體的專業問題，要求學生根據所學的理論、定理或公式設計實驗模型和過程，解決實際問題。主要是培養學生利用所學知識解決實際問題，特別是專業領域問題的能力。

(2) 驗證型實驗。此類實驗需要借助Matlab[13]、R[14]等編程工具，驗證相關定理和公式，使學生對知識點有更加直觀的認識，從而更好地理解和掌握知識點。

2.2 實踐創新能力提升

實踐教學的成果，最終體現在學生的動手能力和應用能力上，而競賽正是學生鍛煉動手能力和應用能力的最好方式。讓學生積極參加國家和省級各類相關競賽，特別是各類數學建模大賽，通過比賽既培養了學生的實際動手能力和邏輯分析能力，也可以為日后走向工作崗位打好基礎。信息技術類專業作為一個對實踐能力要求很強的專業，每年諸如ACM程序設計大賽、信息安全大賽以及省內的軟件設計大賽等競賽項目很多，這類競賽除了考核學生的編程能力之外，在算法的設計和實現部分，也很大程度上鍛煉了學生的數學思維和數學工具的靈活應用能力[15]。

3 信息類專業數學課程實驗教學模式案例

近年來在從事信息技術類相關專業(計算機科學與技術、網絡工程、電子商務、數字媒體技術)的課程教學工作中，在平時的教學科研中，結合概率論與數理統計課程的內容，通過設計型實驗和驗證型實驗的案例，展示如何讓學生結合專業知識進行數學類課程的實驗設計。

3.1 設計型實驗——基于貝葉斯模型的電子郵件分類實驗

電子郵件是網絡用戶工作和生活交流的主要方式，但是，隨著近年來互聯網信息的發展，越來越多垃圾郵件出現在用戶的郵箱里，給用戶正常的生活和工作造成了影響，如何讓計算機自動地對正常郵件和垃圾郵件進行分類是一個重要的問題。郵件分類問題是計算機和人工智能領域的一個重要問題，其基礎理論和模型就是概率論中的貝葉斯模型。而貝葉斯模型是概率論里重要的知識，因此，教學團隊設計了一個利用貝葉斯模型進行郵件分類實驗案例。

實驗內容給定一個郵件數據集，通過全概率公式和貝葉斯公式建立一個分類模型，實現郵件自動分類(正常郵件和垃圾郵件)。

實驗目的通過本實驗，讓學生更加深入地理解和掌握全概率公式和貝葉斯公式，同時給學生展示如何把數學理論和公式與專業領域的應用結合起來。

3.1.1全概率公式和貝葉斯公式

定義1(全概率公式) 設試驗E的樣本空間為S，A為E的事件,B1,B2,…,Bn為樣本空間S的一個劃分,P(Bi)>0 (i=1,2,…,n), 則全概率公式為：

(1)

定義2(貝葉斯公式) 設B1,B2,…,Bn是完備事件組，則對任一事件A，有貝葉斯公式：

(2)

全概率公式是概率論中的重要公式，它將對一個復雜事件A的概率求解問題轉化為對不同情況下發生的簡單事件的概率進行求和的問題。具體步驟是首先建立一個完備事件組的思想，其實就是已知第1階段求第2階段，比如第1階段分為B1,B2,B33種，B1,B2,B3中均有A發生的概率，則第2階段求A的概率為：

P(A)=P(B1)·P(A|B1)+P(B2)·P(A|B2)+

P(B3)·P(A|B3)

(3)

貝葉斯公式，也叫逆概公式，在全概率公式理解的基礎上，其實就是已知第2階段反推第1階段，關鍵是利用條件概率公式做變換，跟上面建立的模型一樣，已知P(A)，求在A發生的條件下Bi發生的概率，這就是貝葉斯公式。具體如下：

(4)

3.1.2郵件的概率模型

實驗情形描述給定兩類郵件集合，分別是垃圾郵件集合B1和正常郵件集合B2，今收到一封新郵件，內容為：“我司可辦理正規發票(保真)，17%增值稅發票點數優惠！”。如何建立模型自動判定此郵件是正常郵件還是垃圾郵件。

實驗步驟

(1) 建立數學模型。令B1=“垃圾郵件”，B2=“正常郵件”，A=“新郵件”，則

(5)

(6)

顯然，新郵件A是否為垃圾郵件的問題轉換為判斷式(5)和(6)哪一個概率值更大的問題，如果P(B1|A)>P(B2|A)，則把郵件A歸類為垃圾郵件集合B1，反之郵件為正常郵件。

(2) 問題簡化。通常情況下概率值P(Bi)是作為先驗知識給定的，而且相等，因此上述問題轉化為比較P(A|B1)和P(A|B2)大小的問題。

(3) 計算給定數據集中垃圾郵件和正常郵件里各自的詞/語句的分布，如表1所示。

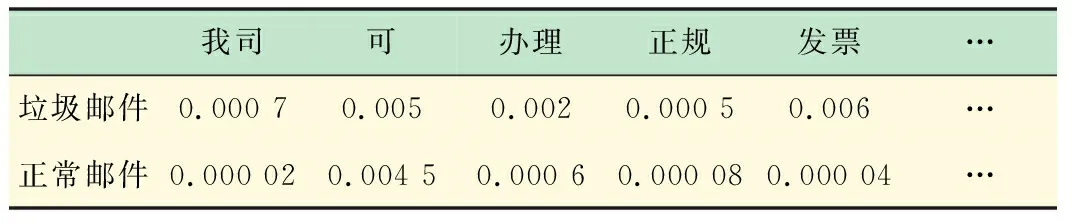
表1 郵件語句內容分布表

根據表1數據，概率值計算如下：

P(A|B1)=P(我司,可,辦理,正規,發票,保真,發票,點數,優惠|垃圾)=2.1×10-14

P(A|B2)=P(我司,可,辦理,正規,發票,保真,發票,點數,優惠|正常)=1.7×10-19

(4) 根據P(A|B1)和P(A|B2)大小做出結論。

以上給出了該實驗的基本步驟，要求學生自己編寫程序實現以上實驗過程。

實驗思考

(1) 該實驗案例中所做假設的合理性，以及對實驗可能造成的影響。

(2) 影響郵件分類精度的因素有哪些？考慮這些因素在實際應用中的影響大小。

3.2 驗證型實驗——高斯信號的分布圖顯示

驗證型實驗的目的是通過實驗來驗證相關定義、公式或定理。本類實驗主要利用Matlab作為程序語言工具[16]，對于典型公式、定理進行編程實現，以符合高斯分布的二維隨機變量為例，進行說明。

在信息技術領域，特別是計算機的數據挖掘領域，經常處理大量的數據，并從數據里挖掘有用的資料和信息。在數據挖掘之前，通常需要觀察一下數據的分布情況，本實驗就是以高斯分布為例進行講述。

實驗內容利用Matlab可視化高斯分布信號的形態。

實驗目的讓學生熟悉如何可視化隨機變量，如何利用Matlab實現隨變量分布的可視化操作。

實驗步驟設定數據參數，可視化高斯分布，結果如圖2所示。

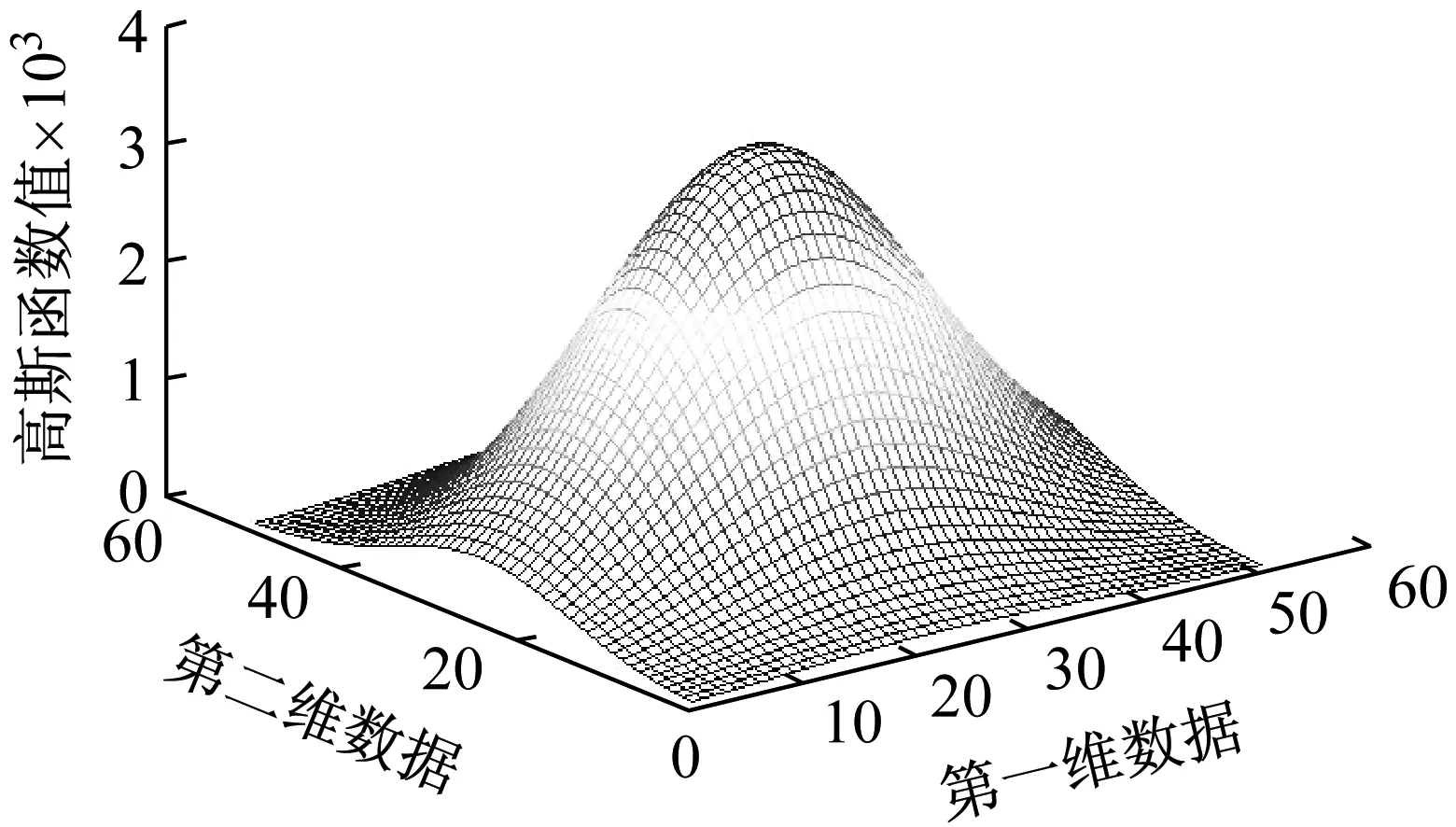
圖2 高斯隨機變量分布圖

主要實驗代碼和結果如下：

u1=0.5; %設定數據第一維的均值

u2=0.6; %設定數據第二維的均值

g1=8; %設定數據第一維的標準差

g2=6; %設定數據第二維的標準差

p=0.1;

[x,y]=meshgrid(-15:0.6:15);

mesh(f);

實驗思考

(1) 符合高斯分布的數據形態有哪些參數決定？

(2) 高斯數據分布的形狀和參數有什么關系？

4 結 語

高校數學課程對專業課程的學習具有重要的幫助，但是現有數學課程的教學模式并沒有和學生的專業知識背景相結合。為此，本文以概率論、數理統計課程為例，以信息技術類專業學生為對象，提出了一種信息技術類專業數學課程實驗教學模式。該實驗教學模式是對數學課程與專業背景結合模式的初步探索，目前作者已經在授課班級進行了初步推廣，學生反映情況良好，下一步，將繼續修正實踐過程中出現的問題，并進一步在其他專業進行推廣。