基于加權信息量與GIS的滑坡易發性評價

胡芹龍，王運生

(1.成都理工大學地質災害防治與地質環境保護國家重點實驗室，四川成都610059；2.成都理工大學環境與土木工程學院，四川成都610059)

0 引 言

GIS技術已經普遍運用到滑坡、泥石流等地質災害的管理中，特別是區域滑坡空間分布規律與易發性評價中。將滑坡的影響因子儲存在GIS中，借助數學模型可實現有效分析與管理。大批學者對三峽庫區滑坡易發性進行研究[1-5]；石菊松等研究了清江隔河巖庫區滑坡分布規律[6]；許沖等對汶川地震滑坡空間分布規律進行了研究[7-10]；在云南、西藏等地質災害高發區，也有很多學者結合GIS和各類模型對災害分布進行預測評價[11-15]。目前，運用較多的模型有層次分析法、信息量模型，邏輯回歸模型等，但部分模型存在一定不足，如層次分析法過分依賴于專家的主觀經驗；信息量模型則忽略了專家的豐富經驗；而加權信息量模型則避免了上述模型的缺點，吸納了兩者的優點，將客觀的信息量與專家觀點同時納入評價體系。

本文選取丹巴縣城及其周邊區域為研究區，基于區內滑坡形成條件和發育特征，運用GIS與加權信息量模型，對滑坡易發程度進行評價，為當地減災防災以及地質災害危險性分析評價提供依據。

1 滑坡易發性評價模型

1.1 研究區概況

丹巴縣位于四川甘孜州東部，在地貌上屬于我國三大階梯中第一、二階梯的過渡帶，為典型高山峽谷地貌，局部地形變化復雜，屬青藏高原型季風氣候區，且具有明顯的垂直分帶性，年降雨量波動較大，且隨海拔高程變化明顯。區內包含大渡河等數條主要河流，滑坡、泥石流等地質災害頻發，典型災害如丹巴縣城后建設街滑坡[16-17]。研究區地理位置見圖1。

1.2 評價方法

信息量法由晏同珍首次在國內運用到滑坡災害的預測中[18]，用各影響因子的信息量值來預估滑坡產生難易程度，可用下式表達

(1)

式中，S為研究區單元數量之和；N為發育滑坡的單元數量之和；Si為影響因子Xi中包含的單元數量之和；Ni為評價因素Xi內所對應的滑坡單元總數。某一評價單元的信息量值可表示為

(2)

式中，Ii代表相應評價因素的信息量；n為評價因子數量。該評價因素的信息量值代表該因素對滑坡易發程度貢獻大小，值越大代表該因素對滑坡發生越有利。

層次分析(AHP)法主要根據層次決策各個因子的權重占比，其優點是根據專家打分，使得專家經驗能夠參與決策過程。評價具體步驟如下：

(1)構造判斷矩陣。對于X1，X2，…，Xn個評價指標，由專家組將各個指標兩兩作對比得判斷矩陣X。

(2)確定權值。假設存在某相同階數的正向量A，使XA=λmaxA成立，λmax為X的最大特征值，A為λmax的特征向量。解矩陣方程X，其各分量解即為所對應的X1，X2，…，Xn的權值。本文將AHP法與信息量模型結合，即得到評價因子的加權信息量模型，進而運用到滑坡的易發性程度評價之中。

2 基于GIS的滑坡易發性評價

2.1 因子選取

滑坡通常由自身地質環境控制，外部動力環境因素誘發。前者主要指地層巖性、地形地貌、地質構造等，后者主要指降雨、地震及人類工程活動等。本文選取巖組、斜坡結構、坡度、地質構造、河流水系、變形跡象、人類工程活動等7大類因子。

2.2 評價指標體系

(1)工程地質巖組。根據研究區巖組工程地質特征，可分為5大巖體，即堅硬類巖體、較堅硬類巖體、較軟弱類巖體和軟弱類巖體以及松散類巖體。不同工程地質巖組分布見圖2。

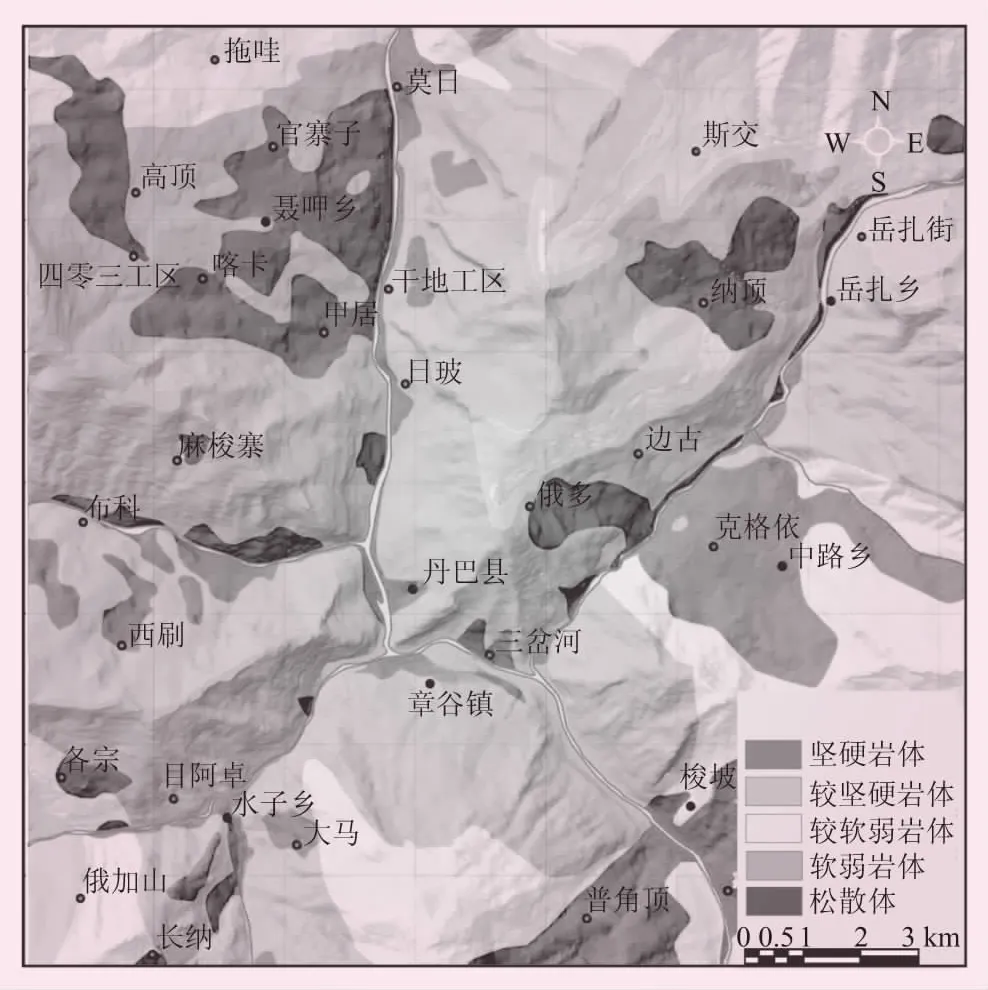
圖2 不同工程地質巖組分布

(2)斜坡結構。研究區滑坡多發育于松散土體、順向坡中，根據斜坡結構特征，將斜坡按斜坡類型劃分為松散體坡、順向坡、斜交坡、橫向坡、逆向坡等5大類。斜坡結構因子分級見圖3。

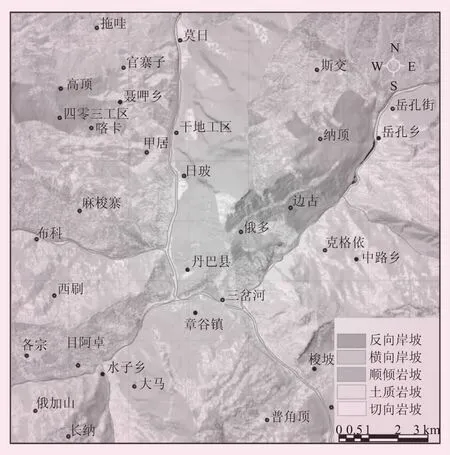
圖3 斜坡結構因子分級

(3)地形坡度。坡度不同，地表水的徑流方式及應力分布也不同，這對滑坡影響較大，將地形坡度分為[0，20)、[20，30)、[30，40)、[40，50)、[50，90)等5個區間。地形坡度因子分級見圖4。

圖4 地形坡度因子分級

(4)地質構造。研究區先后經歷了多次造山運動與地殼抬升，在GIS中根據斷裂構造帶的影響距離進行分級，按0～100、100～200、200～300 m以及>300 m分級。地質構造因子分級見圖5。

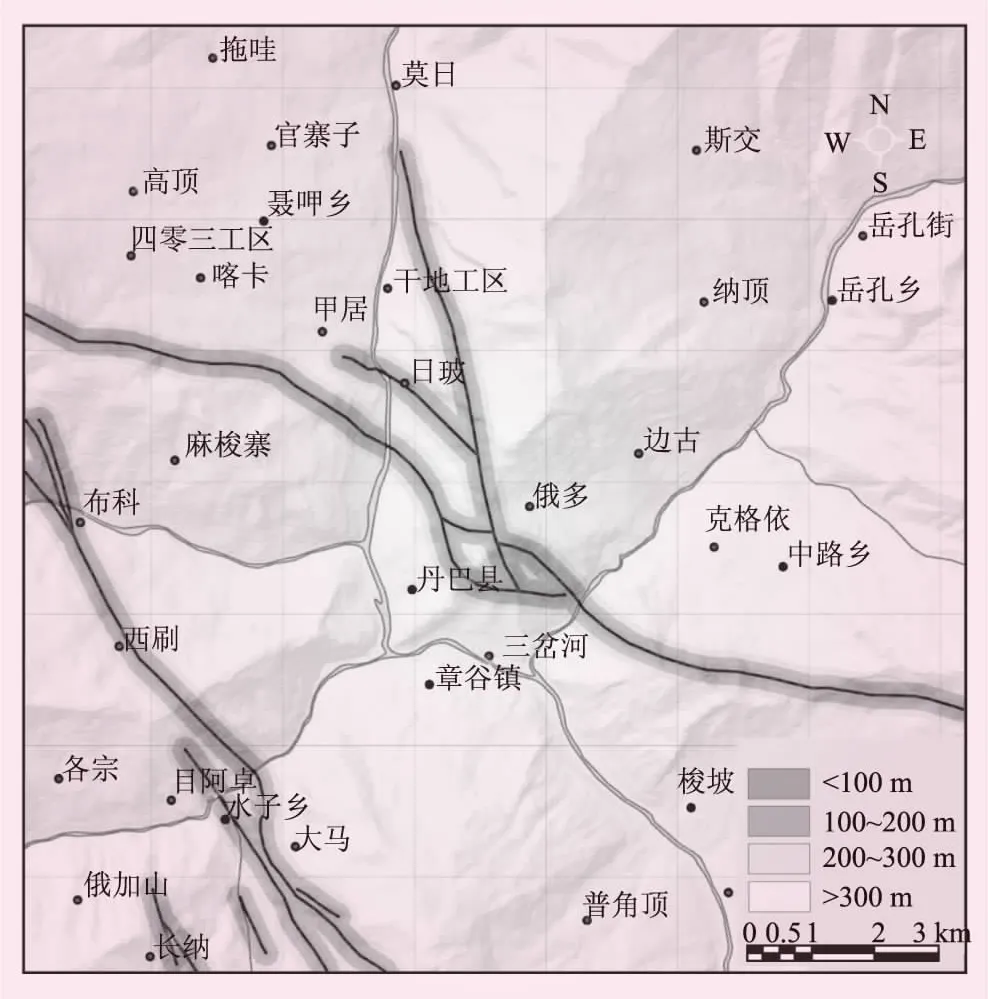
圖5 地質構造因子分級

(5) 河流影響。河流侵蝕對兩岸滑坡起到了重要影響，按河流侵蝕切割影響距離，分0～100、100～200、200～300 m以及>300 m等4級。河流因子分級見圖6。

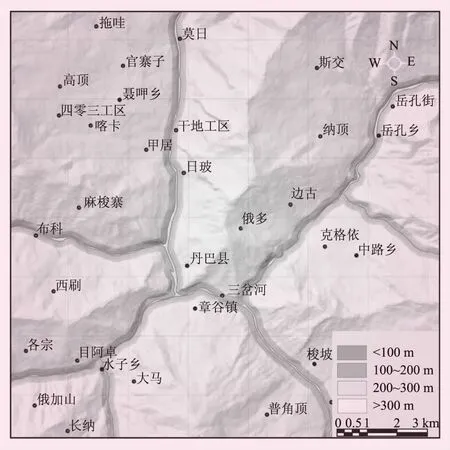
圖6 河流因子分級

(6)變形跡象。研究區發生某一滑坡后，常在其附近形成某些新的滑坡。為此，將已發生滑坡的變形跡象納入局部區域評價指標，據斜坡變形發展狀況將其劃分為強變形、中等變形、弱變形、無變形等4級。變形歷史因子分級見圖7。

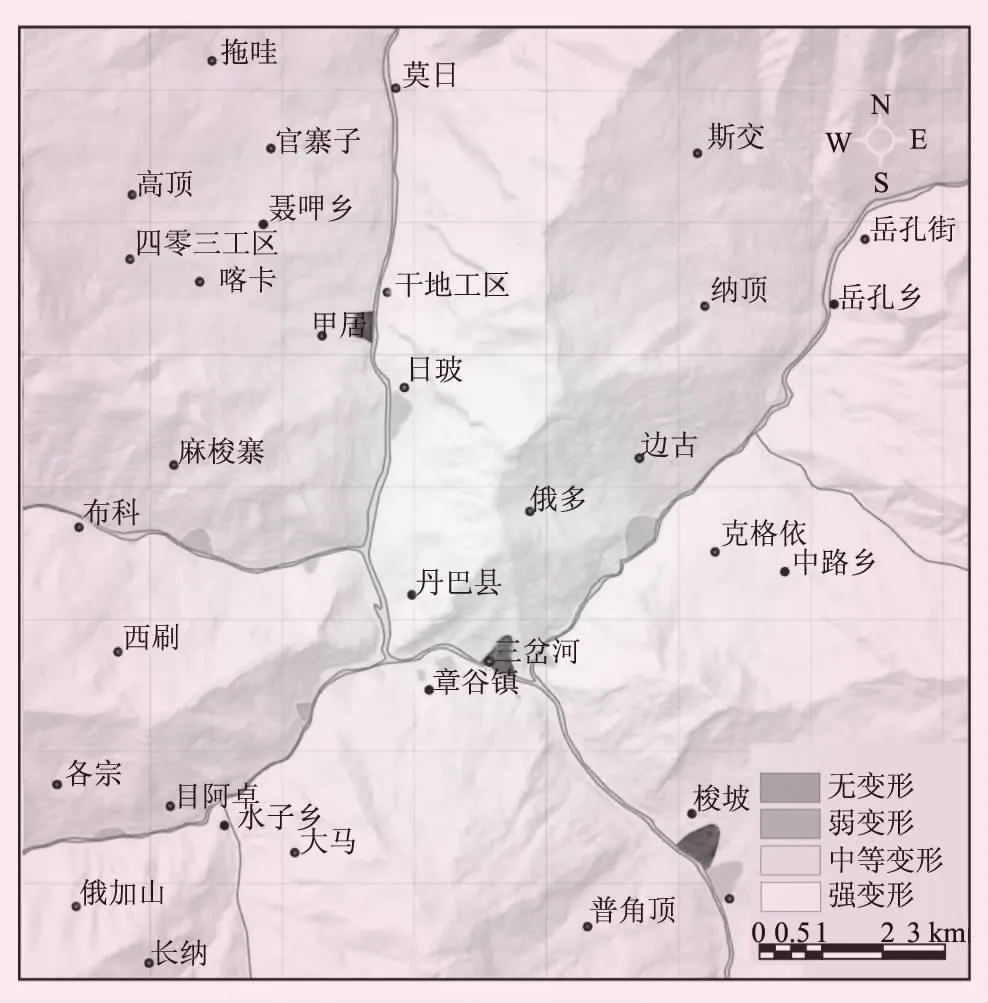
圖7 變形歷史因子分級

(7) 人類工程活動。區內人類工程活動主要為公路修建，邊坡開挖誘發崩塌滑坡，按距離道路距離分0～10、10～20、20～40 m以及>40 m等4級。人類工程活動因子分級見圖8。

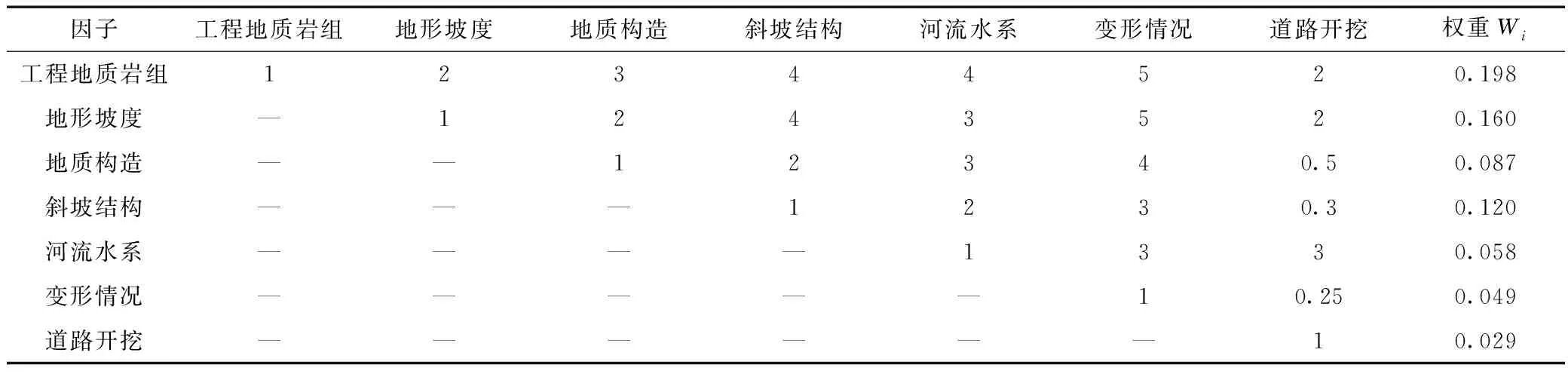
表2 因子權重的配對比較矩陣

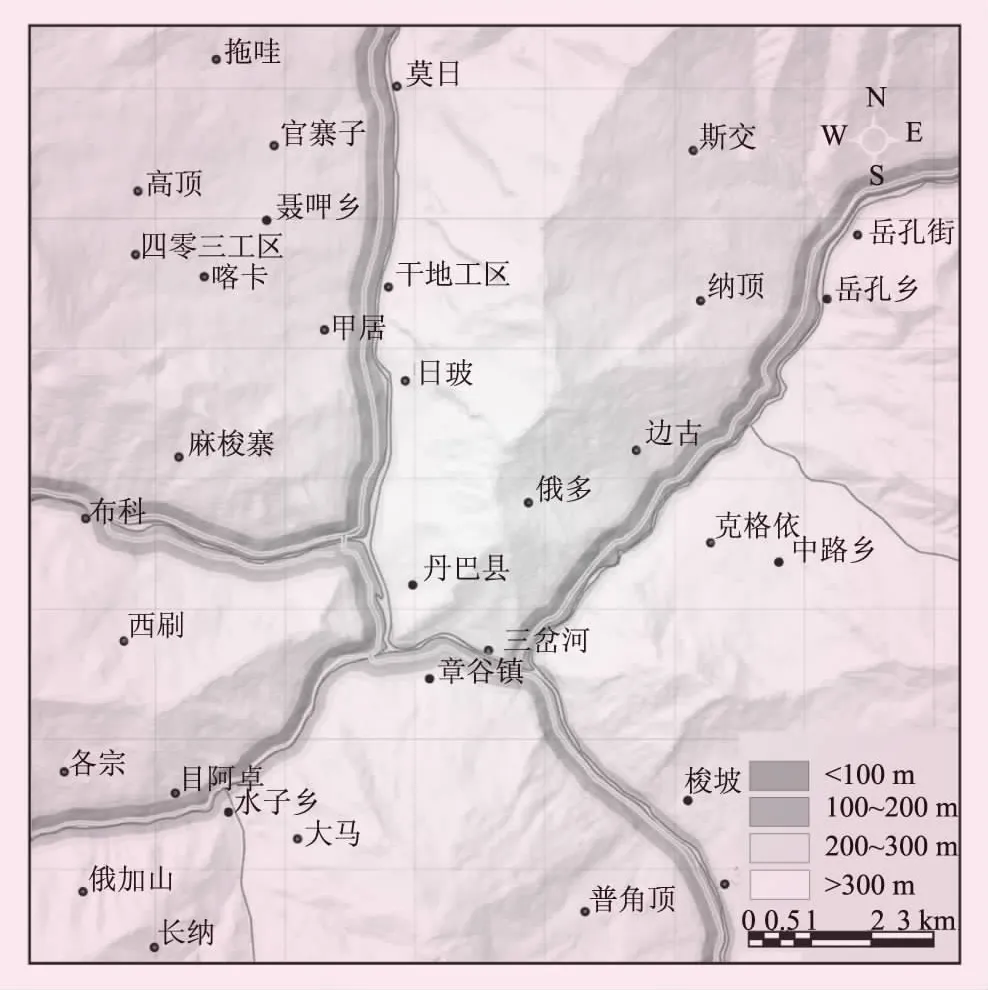
圖8 人類工程活動因子分級

2.3 滑坡易發性分區

根據AHP法，專家對各個因子兩兩對比打分，得到判斷矩陣，再基于MATLAB對判斷矩陣進行求解，經歸一化處理即得各個因子權重。因子權重的配對比較矩陣見表2。

本次判斷矩陣解算得λmax=8.352、一致性指標CI=0.05、 隨機一致性指標RI=1.14、CR=CI/RI=0.04。由CR<0.1可知，該判斷矩陣具備滿意的一致性。結合加權信息量模型，運用GIS空間分析功能，實現對研究區滑坡地質災害易發性區劃。滑坡易發性評價見圖9。從圖9可知：

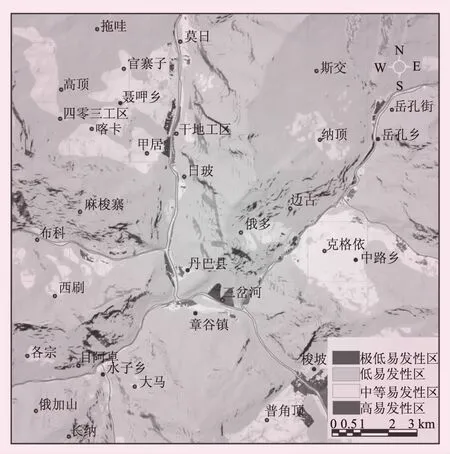
圖9 滑坡易發性評價

(1)高危險區。位于丹巴縣城、大渡河及其主要支流兩岸邊上的斜坡，面積0.582 km2，占研究區面積的0.27%。該分布段緩坡較多，溝口沖洪積扇適合人類居住，人口較多，城鎮建設活動較多，地質條件與人類工程活動共同導致滑坡災害發育。

該區內發育滑坡6處。其中，小型滑坡1處，中型滑坡2處，大型滑坡3處。

(2)中等危險區。多分布在高程2 000～3 100 m的斜坡帶，面積12.16 km2，占研究區面積的5.74%。該區內人類工程活動明顯減弱，主要是一些農業耕植和零散的房屋建設，滑坡少有發生，一般不具危害性，區內發育滑坡4個。

(3)低危險區。分布于丹巴縣城5大水系周邊海拔高度3 000 m以上地區，包括丹巴縣各鄉部分地區，面積120.69 km2，占總面積的57%。該區內滑坡很少發生，一般不具危害性。

(4)極低危險區。分布于丹巴縣5大水系較遠的海拔高度3 000 m以上地區，面積78.47 km2，占總面積37%。該區內滑坡不發生，一般不具危害性。

2.4 評價結果精度

選用ROC曲線對結果進行精度評價，ROC曲線是以假陽性率即1-特異度為橫坐標，以真陽性率即靈敏度為縱坐標繪制而成。1-特異度即未發生災害單元被正確預測的比例，靈敏度即災害單元被正確預測的比例。使用曲線下面積(AUC)來衡量評價預測精度，AUC值越大說明模型應用越成功、預測效果將越好[14]。在MATLAB中輸入加權信息量模型的預測值和診斷值，并繪制得到ROC曲線(見圖10)。從圖10可知，AUC值達83.6%，認為該評價結果精度較高，效果良好，可用于該地區的滑坡易發性評價。

圖10 滑坡易發性預測的ROC曲線

3 結 語

本文選取了巖組、斜坡結構、斜坡坡度、地質構造、河流水系、變形跡象、人類工程活動等7大類因子，在GIS平臺中建立影響因子數據庫，對丹巴縣滑坡空間分布規律的分析，得出以下結論：

(2)將AHP法求解得到各指標的因子權重結果與信息量模型進行結合，得到了既有專家經驗，又遵循客觀數據的加權信息量模型，為滑坡易發性評價奠定基礎。

(3)基于GIS與加權信息量模型，實現了對研究區滑坡地質災害易發性區劃，高危險區與中等危險區分別占總面積的0.27%、5.74%，絕大部分地區(94%)為低或極低易發區。