基于離散灰色模型的電力應急物資分配模型研究

樂恩典

（國網舟山市供電公司，浙江舟山316000）

0 引言

作為現代城市運行的重要支撐，電力提供了人們工作、生活所需的能源，對于保障社會穩定和經濟發展起到了舉足輕重的作用，在保障國民經濟發展的同時也保證了人民幸福快樂地生活。但由于自然災害以及部分人為操作因素影響，電力基礎設施會出現損壞，發生大面積停電事故，這對于電力公司的搶修工作是一種極大的考驗，而其中最耗費時間和人力的就是電力物資的調動問題，故如何在非常時期高效地調動物資，開展故障搶修作業得到了廣泛的研究。

國內外均對電力物資調度進行了大量研究。文獻[2]根據車輛調度過程中可能干擾車輛管理的事件設置干擾因子并建立模糊窗口的車輛管理模型，對車輛調度進行分析。文獻[3]對物資存儲使用情況進行分析，引入概率模型對故障和物資之間的關系建模，從而分析最優物資調度問題。

上述文獻沒有綜合考慮物資車輛環境等實時數據對搶修地點的到達概率時間以及目標的相對重要性，本文將對此進行研究分析。

1 基于離散灰色概率的電力應急物資運輸路徑選擇模型

對于電力搶修物資配送，主要需考慮兩個問題：

（1）電力物資的路徑選擇；

（2）電力物資運送的過程中受到哪些因素影響和干擾。

其中，車輛所選擇的路徑應盡可能短，干擾因素應盡可能少，達到搶修地點應盡可能快。

對于干擾項，由于其不確定性，本文采用離散灰色模型，通過歷史同類型數據進行相應預測，模糊判斷給出路徑以及車輛管理中會遇到的某些影響搶修時間的概率值，從而實現最優路徑的選取。

對于一個電網，可以將其看作一個網絡圖G，本文考慮車輛在運輸過程中的擁堵、交通故障、天氣等，令ω（e）為擁擠程度因子，ω（e）為ε（e）=0的情況下通過該路段所花費的時間，P（e）為在發生電力突發事故時發生交通故障的概率值，δ為電力突發事故對城市交通的影響因子。為最終物資到達搶修地點需要花的時間，車輛在該預測下到達搶修地點的概率值服從平均分布：其中，

2 基于合理度函數的多目標優化模型

2.1 合理度函數的構建

2.1.1 時間合理度函數

在考慮各種因素的情況下，受到搶修時間限制時，為量化物資運送到搶修地點的時間快慢程度，可建立時間合理度函數如下：

式中，αj為受災區j對時間的敏感系數。

合理度期望如式（3）所示：

其中，ω（Pj）為在沒有發生交通故障情況下，受災區j的第一批物資到達的時間，且必然有ω（Pj）≤tjd。

2.1.2 物資合理度函數

搶修地點j對于電力應急物資k數量的合理度函數如式（4）所示：

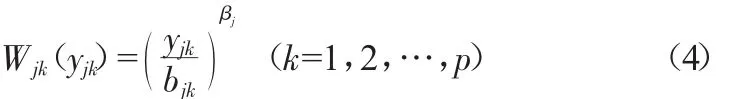
式中，βj為物資需求程度。

2.2 約束條件

在需要大量搶修物資的情況下，考慮到本地區沒有辦法滿足電力物資供應，需要考慮從外區進行物資的調度，其關系式如下所示：

每個電力應急物資儲備庫可提供的物資時間函數為tj=min（Tjk），則有如下約束關系：

3 基于目標相對重要性的改進多目標進化優化方法

在考慮多目標函數優化的過程中，需要建立兩個目標之間的關系模型，其步驟如下：

步驟1：初始化種群P（0）；

步驟2：根據電力搶修地點構建目標的數學模型；

步驟3：執行離散、模糊、選擇、交叉等遺傳操作，生成臨時種群Q（r）；

步驟4：將P（r）和Q（r）合為R（r），根據重要性和合理度來排序；

步驟5：如果結果不收斂繼續執行第2步，如果收斂則得到最優路徑。

4 算例分析

本文以IEEE14節點系統為例，假設其中有7個節點發生故障，其中物資存儲量、物資需求量如圖1所示，圖中故障點為5、6、8、9、10、15、16等7個節點，電力物資倉庫為3、4、12節點。

圖1 電力應急交通網絡圖

各受災區的物資需求數量和電力應急物資儲備庫的物資存儲數量如表1和表2所示。

表1 物資需求數量

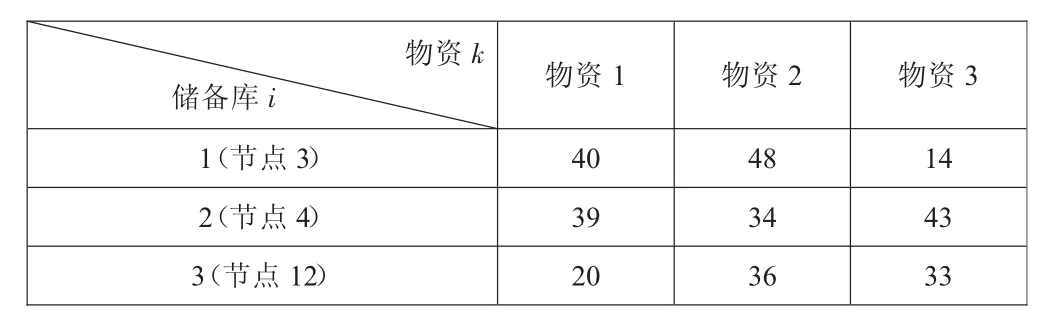
表2 物資儲存數量

α1～α7分別取3、5、3、4、1、2、6，β1～β7分別取1、2、4、3、6、1、3，λ1～λ3分別取0.3、0.5、0.2，運算結果如表3所示。

表3 物資分配的運算結果

當進化優化算法的種群為第46、47、48代時，物資運輸分配情況基本穩定，適應度的值也趨于平局值，此時的物資分配達到最優，不妨取第48代種群為最優種群，此時即為物資調度的最優解。

5 結語

本文運用離散灰色模型對電力系統故障搶修期間物資調配的選擇進行了合理估計，考慮到物資供應地點的成本、車輛調度、交通擁堵程度、故障概率等建立了運輸路徑選擇模型和時間、物資合理度函數，并求得最優解，因而有一定的實踐價值。